Structured Learning Sequence Labeling Problem Hungyi Lee Sequence

Structured Learning Sequence Labeling Problem Hung-yi Lee
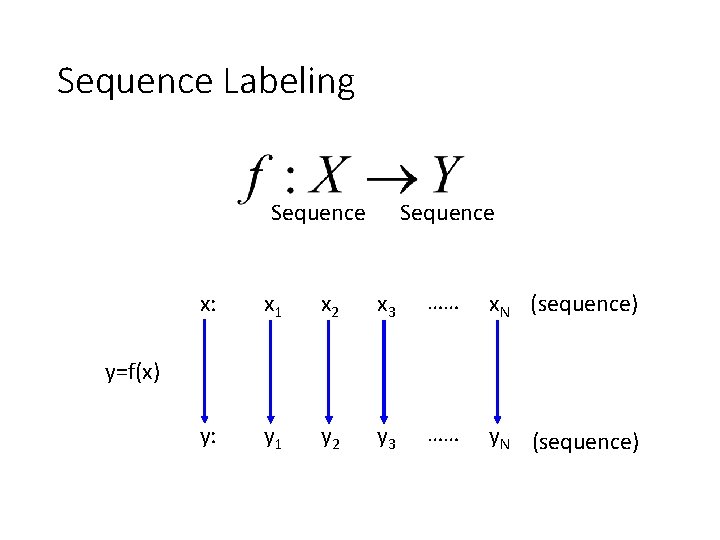
Sequence Labeling Sequence x: x 1 x 2 x 3 …… x. N (sequence) y: y 1 y 2 y 3 …… y. N (sequence) y=f(x)

Sequence Labeling - Application • Name entity recognition • Identifying names of people, places, organizations, etc. from a sentence • Harry Potter is a student of Hogwarts and lived on Privet Drive. • people, organizations, places, not a name entity • Information extraction • Extract pieces of information relevant to a specific application, e. g. flight booking • I would like to leave Boston on November 2 nd arrive in Taipei before 2 p. m. • place of departure, destination, time of departure, time of arrival, other
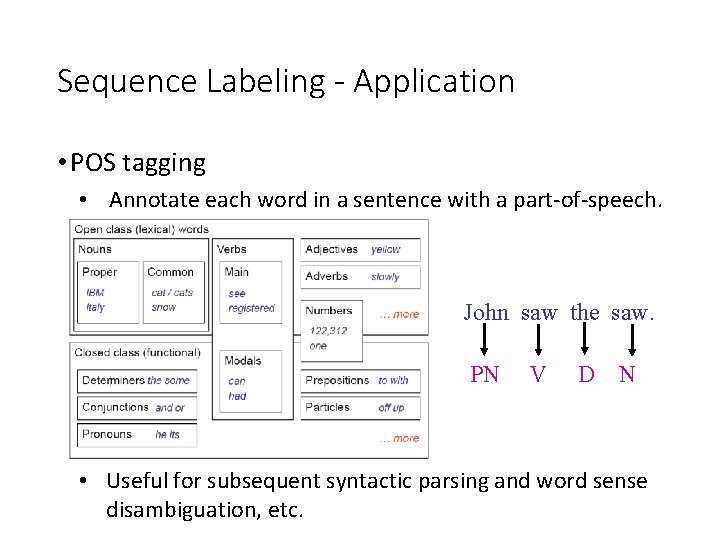
Sequence Labeling - Application • POS tagging • Annotate each word in a sentence with a part-of-speech. John saw the saw. PN V D N • Useful for subsequent syntactic parsing and word sense disambiguation, etc.
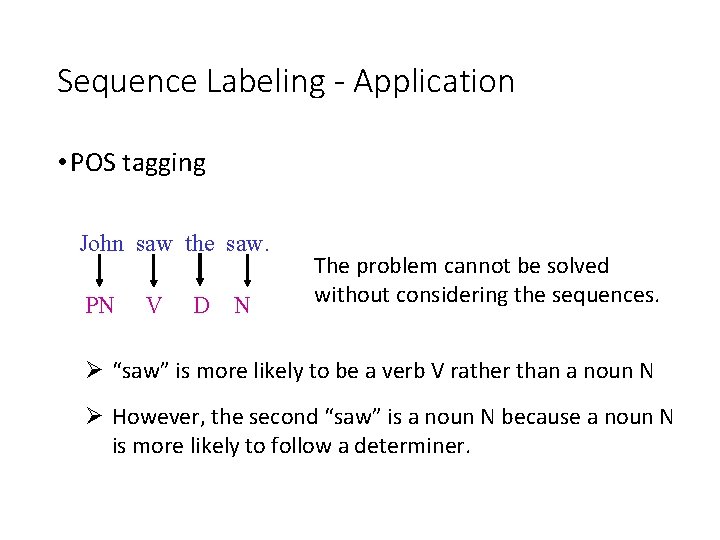
Sequence Labeling - Application • POS tagging John saw the saw. PN V D N The problem cannot be solved without considering the sequences. Ø “saw” is more likely to be a verb V rather than a noun N Ø However, the second “saw” is a noun N because a noun N is more likely to follow a determiner.
Outline Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments
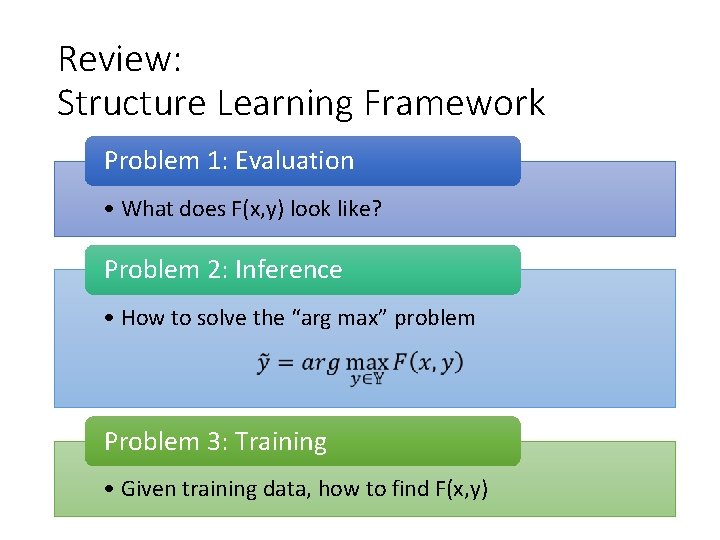
Review: Structure Learning Framework Problem 1: Evaluation • What does F(x, y) look like? Problem 2: Inference • How to solve the “arg max” problem Problem 3: Training • Given training data, how to find F(x, y)
Outline Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments

HMM - Evaluation • F(x, y) = P(x, y) =P(y)P(x|y) Transition probability: Emission probability: x: John saw the saw. y: PN V D N

HMM - Evaluation Example x: The dog ate the homework. y: start D N V D P(x, y)=P(y)P(x|y) N end

HMM - Inference • Enumerate all possible y • Assume there are |S| tags, and the length of sequence y is n • There are |S|n possible y • Greedy algorithm • Not necessary find the best solution • Viterbi algorithm • Please refer to the slides of HW 2 Open Question: influence of non-exact inference

HMM - Training • Obtain P(x, y) from training data Training Data: ……

HMM - Training So simple

HMM - Drawbacks • Inference: • To obtain correct results … Can HMM guarantee that? not necessarily small xi=a xi=c 1/2 Transition probability: yi=V 9/10 …… P(V|N)=9/10 P(D|N)=1/10 Emission probability: P(a|V)=1/2 P(a|D)=1 …… yi-1=N 1/10 xi=a 1 yi=D

HMM - Drawbacks • Inference: • To obtain correct results … Can HMM guarantee that? not necessarily small Transition probability: xi=a P(V|N)=9/10 P(D|N)=1/10 …… Emission probability: P(a|V)=1/2 P(a|D)=1 …… P(xi|yi) yi-1=N P(yi|yi 1) yi=? V
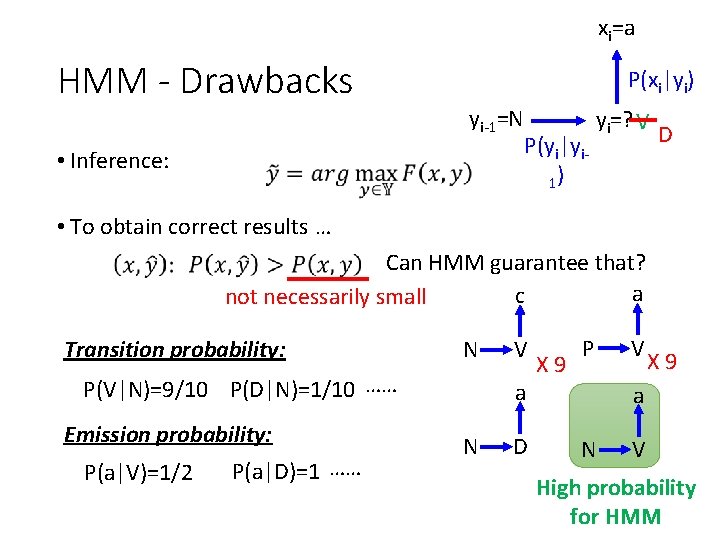
xi=a HMM - Drawbacks P(xi|yi) yi-1=N • Inference: P(yi|yi 1) yi=? V D • To obtain correct results … Can HMM guarantee that? a c not necessarily small Transition probability: N P(V|N)=9/10 P(D|N)=1/10 …… Emission probability: P(a|V)=1/2 P(a|D)=1 …… V a N D X 9 P V X 9 a N V High probability for HMM
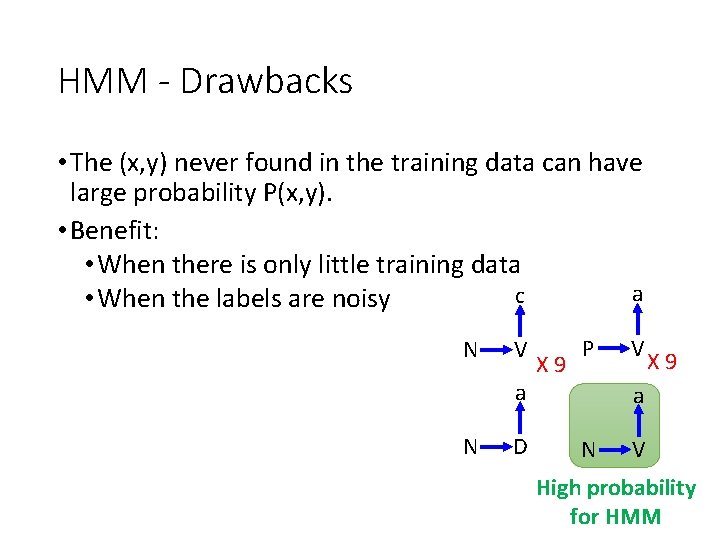
HMM - Drawbacks • The (x, y) never found in the training data can have large probability P(x, y). • Benefit: • When there is only little training data a c • When the labels are noisy N V a N D X 9 P V X 9 a N V High probability for HMM
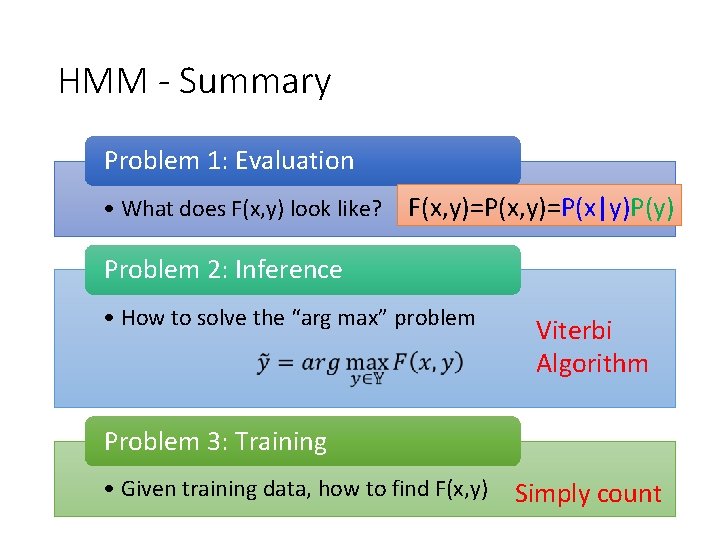
HMM - Summary Problem 1: Evaluation • What does F(x, y) look like? F(x, y)=P(x|y)P(y) Problem 2: Inference • How to solve the “arg max” problem Viterbi Algorithm Problem 3: Training • Given training data, how to find F(x, y) Simply count
Outline Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments

CRF – Evaluation • Evaluation Function (different from HMM? )

Value CRF – Evaluation x: The dog ate the homework. y: D N V D N • If there are |S| possible tags, |T| possible words Part 1 has |S| X |T| dimensions D, the 2 D, dog 0 D, ate 0 D, homework 0 …… …… N, the 0 N, dog 1 N, ate 0 N, homework 1 …… …… V, the 0 V, dog 0 V, ate 1 V, homework 0 …… ……
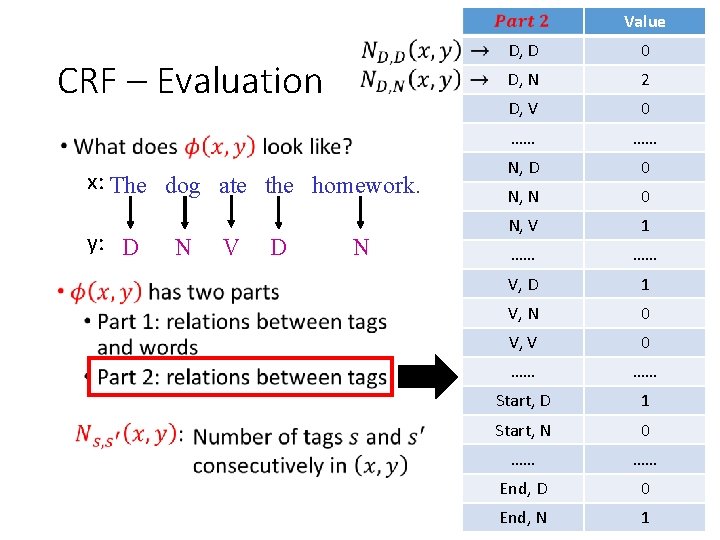
Value CRF – Evaluation x: The dog ate the homework. y: D • N V D N D, D 0 D, N 2 D, V 0 …… …… N, D 0 N, N 0 N, V 1 …… …… V, D 1 V, N 0 V, V 0 …… …… Start, D 1 Start, N 0 …… …… End, D 0 End, N 1
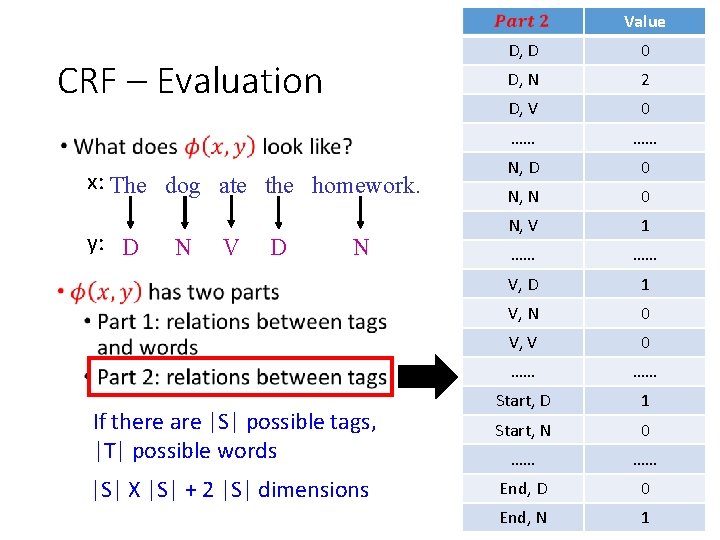
Value D, D 0 D, N 2 D, V 0 …… …… N, D 0 N, N 0 N, V 1 …… …… V, D 1 V, N 0 V, V 0 …… …… If there are |S| possible tags, |T| possible words Start, D 1 Start, N 0 …… …… |S| X |S| + 2 |S| dimensions End, D 0 End, N 1 CRF – Evaluation x: The dog ate the homework. y: D N V D N •

CRF – Evaluation • Recall HMM: means
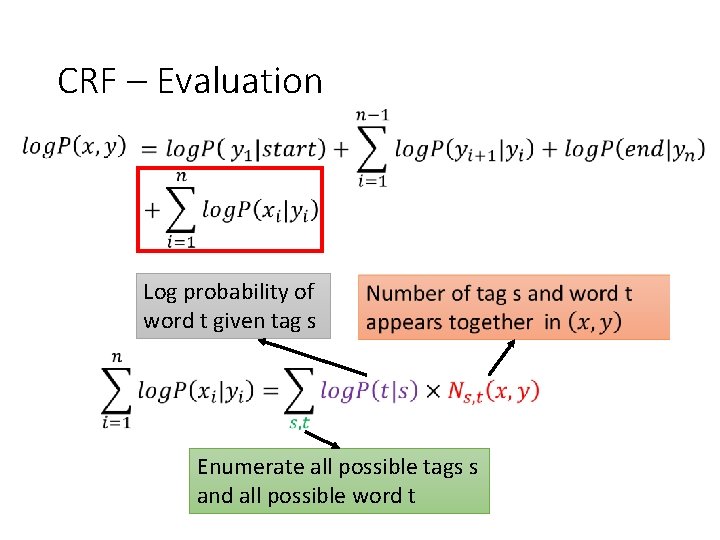
CRF – Evaluation Log probability of word t given tag s Enumerate all possible tags s and all possible word t

CRF – Evaluation x: The dog ate the homework. y: D N V D N (for any other s and t)

CRF – Evaluation

CRF – Evaluation

CRF – Evaluation means

CRF – Inference • Inference Done by Viterbi as well Only depending on x, not depending on y

CRF - Training • Maximize what we observed Minimize what we don’t observed

CRF - Training Gradient descent Opposite direction of the gradient Gradient Ascent The same direction of the gradient

CRF - Training Compute

CRF - Training

CRF - Training Can be computed by Viterbi algorithm as well

CRF - Training

CRF - Training Stochastic Version:
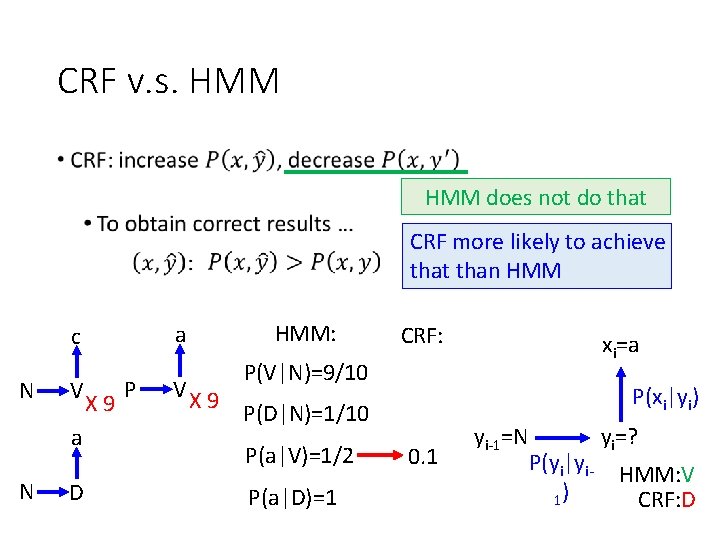
CRF v. s. HMM • HMM does not do that CRF more likely to achieve that than HMM a c N V a N D X 9 P VX 9 HMM: CRF: xi=a P(V|N)=9/10 P(xi|yi) P(D|N)=1/10 P(a|V)=1/2 P(a|D)=1 0. 1 yi-1=N P(yi|yi 1) yi=? HMM: V CRF: D

CRF v. s. HMM • Too sparse… Method 1: Inaccurate assumption Method 2. Give the distribution some assumptions?
CRF- Summary Problem 1: Evaluation Problem 2: Inference Problem 3: Training
Outline Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments

Review: Structured Linear Model • Evaluation: Directly apply on sequence labeling? The same as CRF • Inference: Viterbi • Training: • Target: • Algorithm: Structured Perceptron

Structured Perceptron v. s. CRF • Training algorithm for Structured Perceptron Hard • Training algorithm for CRF (stochastic version) =1 Soft
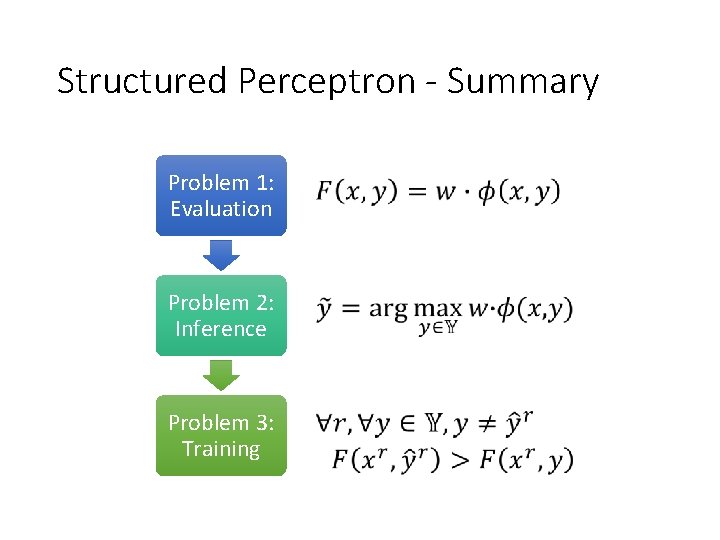
Structured Perceptron - Summary Problem 1: Evaluation Problem 2: Inference Problem 3: Training

Outline Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments

Structured SVM • Evaluation and inference is the same as structured perceptron, but with different training method. • Evaluation: • Inference: • Training: Minimize a cost function • Can be done by solving a quadratic programming problem as SVM • Note: below the discussion for structured SVM is not limited to sequence labelling

Structured SVM – Objective Function • Example 1 A T T C G G A T T A G G A A Example 2

Structured SVM – Objective Function • Error on the training data with weight vector w

Structured SVM – Upper Bound

Structured SVM – Upper Bound Meaningful?

Structured SVM – Upper Bound Assume =0 (contradiction)

Structured SVM – Upper Bound margin c. f. structured perceptron:

Structured SVM – Regularization Which one should be selected ? Choose the “smaller” one Regularization

Structured SVM – Regularization Training Data: Testing data: Training data and testing data can have different distribution ? Smaller w can minimize the influence of mismatch

Structured SVM – Regularization (you can also add regularization term in CRF training ) Way 1. Gradient descent Ref: http: //svivek. com/teaching/structured-prediction/fall 2014/lectures/8 -trainingstrategies/training-strategies. pdf Way 2. Solving Quadratic programming (QP) problem as SVM

Structured SVM – Solving QP

Structured SVM – Solving QP Slack variable
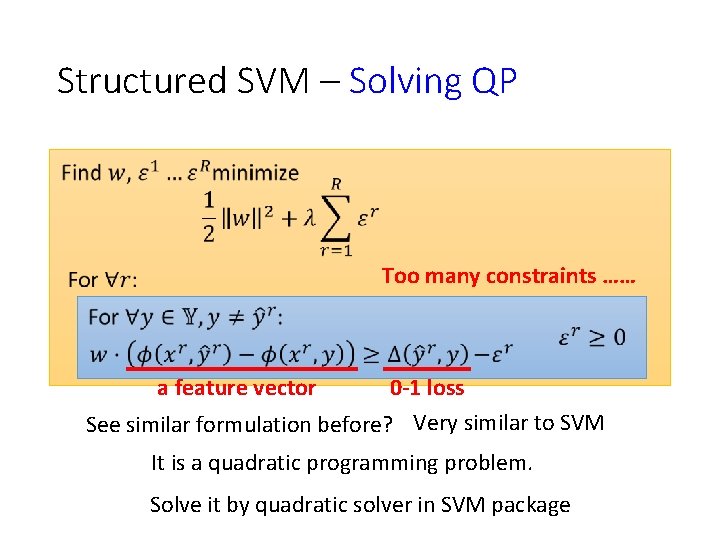
Structured SVM – Solving QP Too many constraints …… a feature vector 0 -1 loss See similar formulation before? Very similar to SVM It is a quadratic programming problem. Solve it by quadratic solver in SVM package
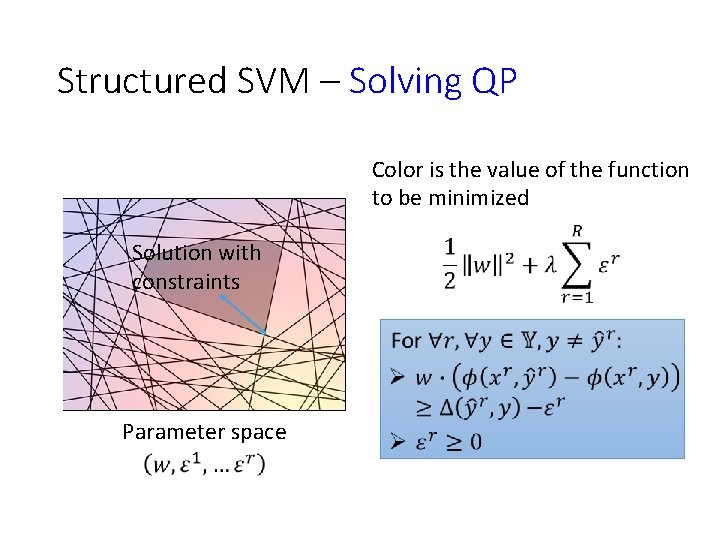
Structured SVM – Solving QP Color is the value of the function to be minimized Solution with constraints Solution without constraints Parameter space
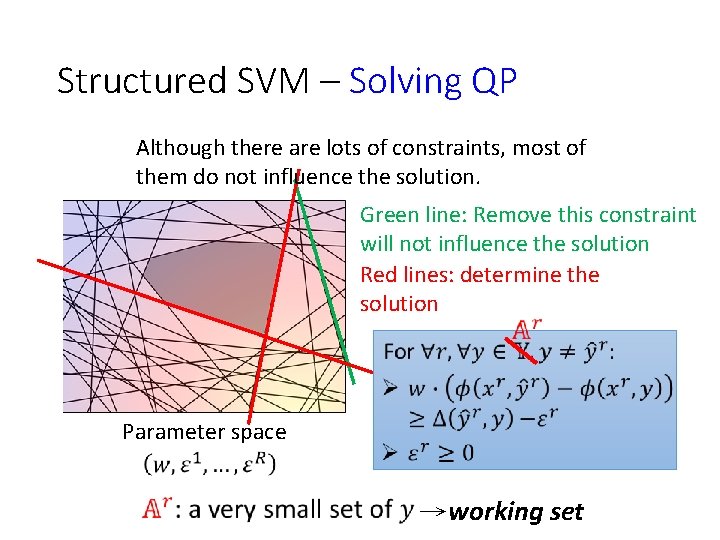
Structured SVM – Solving QP Although there are lots of constraints, most of them do not influence the solution. Green line: Remove this constraint will not influence the solution Red lines: determine the solution Parameter space →working set
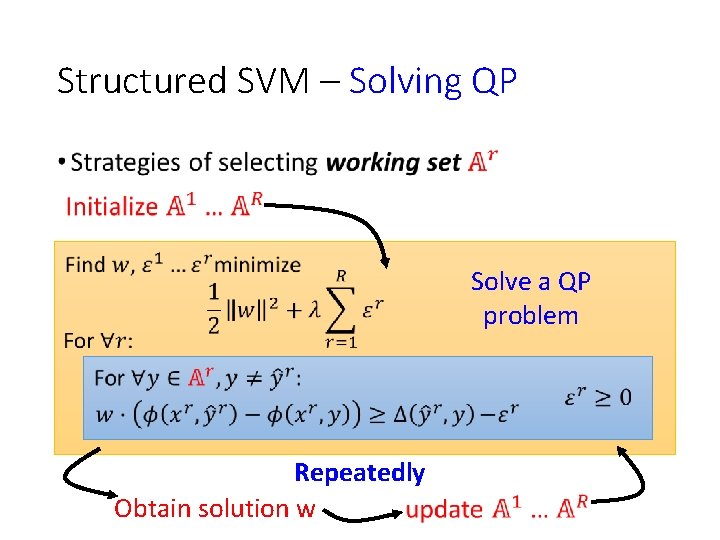
Structured SVM – Solving QP • Solve a QP problem Repeatedly Obtain solution w
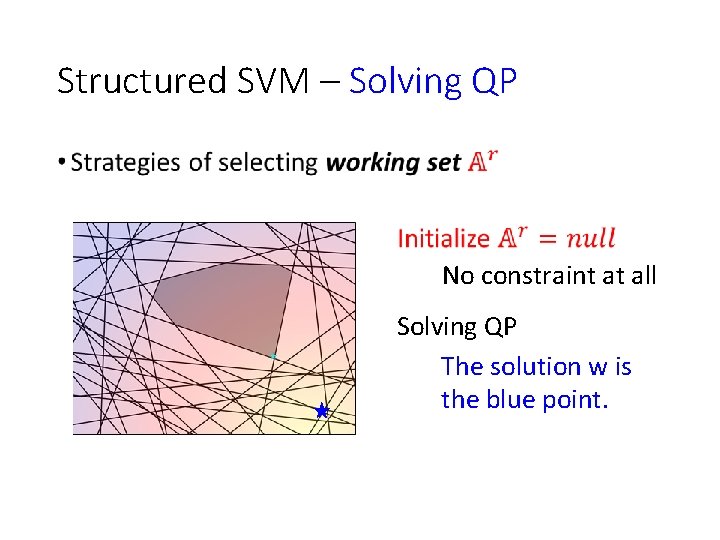
Structured SVM – Solving QP • No constraint at all Solving QP The solution w is the blue point.
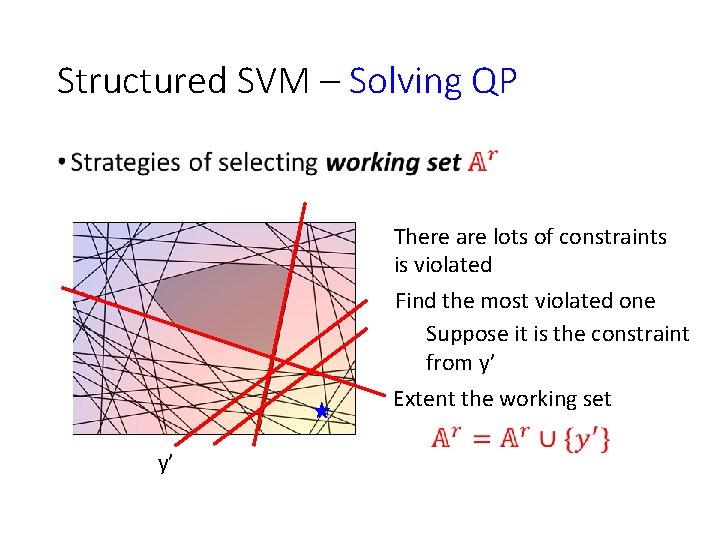
Structured SVM – Solving QP • There are lots of constraints is violated Find the most violated one Suppose it is the constraint from y’ Extent the working set y’
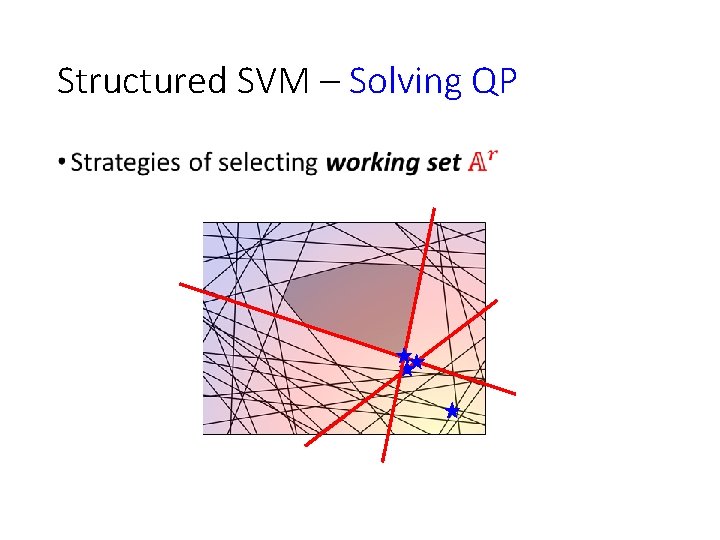
Structured SVM – Solving QP •

Framework of Structured SVM • (why? )

Framework of Structured SVM Training Given training data: Repeat For r=I, …, R: Testing

More about Structured SVM Margin rescaling: Slack variable rescaling:
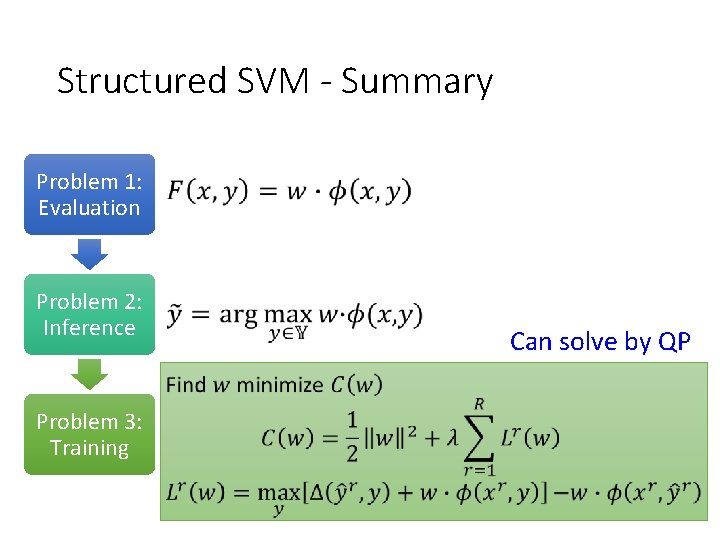
Structured SVM - Summary Problem 1: Evaluation Problem 2: Inference Problem 3: Training Can solve by QP
Outline (details are in the next week) Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments
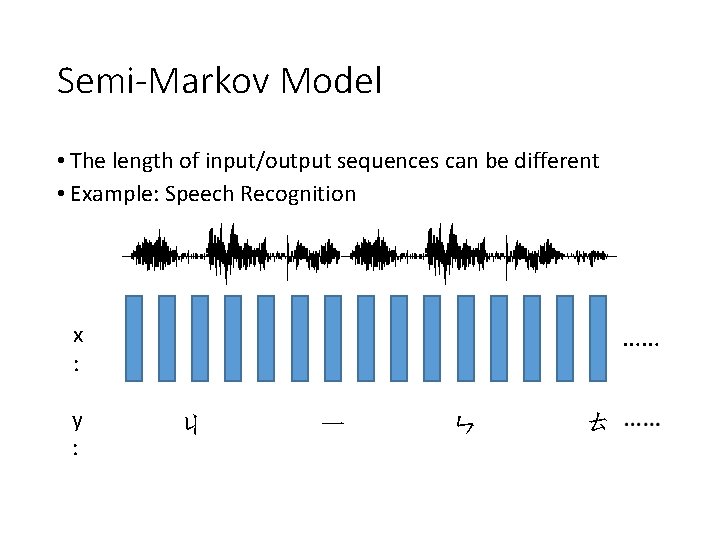
Semi-Markov Model • The length of input/output sequences can be different • Example: Speech Recognition …… x : y : ㄐ 一 ㄣ ㄊ
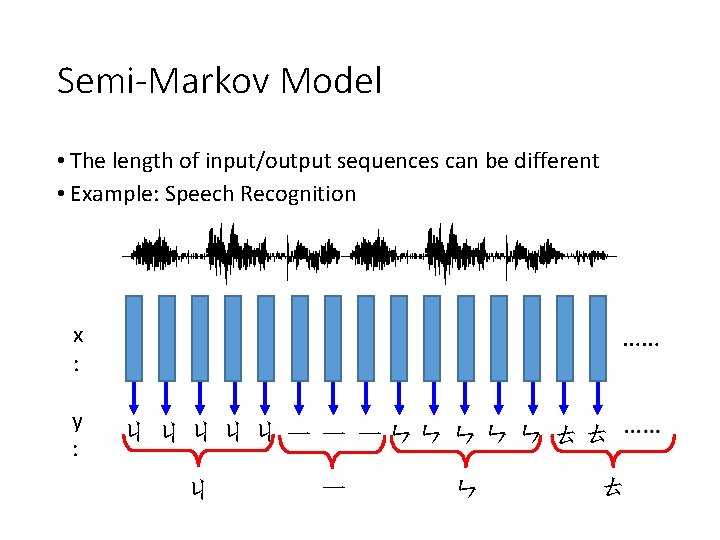
Semi-Markov Model • The length of input/output sequences can be different • Example: Speech Recognition …… x : y : ㄐ ㄐ ㄐ 一 一 一ㄣㄣ ㄣ ㄊㄊ ㄐ 一 ㄣ ㄊ
Semi-Markov Model • The length of input/output sequences can be different • Example: Speech Recognition …… x : y : ㄐ 一 Can we do that? ㄣ ㄊ
Outline Hidden Markov Model (HMM) Conditional Random Field (CRF) Structured Perceptron Structured SVM Semi-Markov Models Some Experiments

Synthetic Data • Ref: John D. Lafferty, Andrew Mc. Callum, and Fernando C. N. Pereira. 2001, “Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data”, ICML, 2001
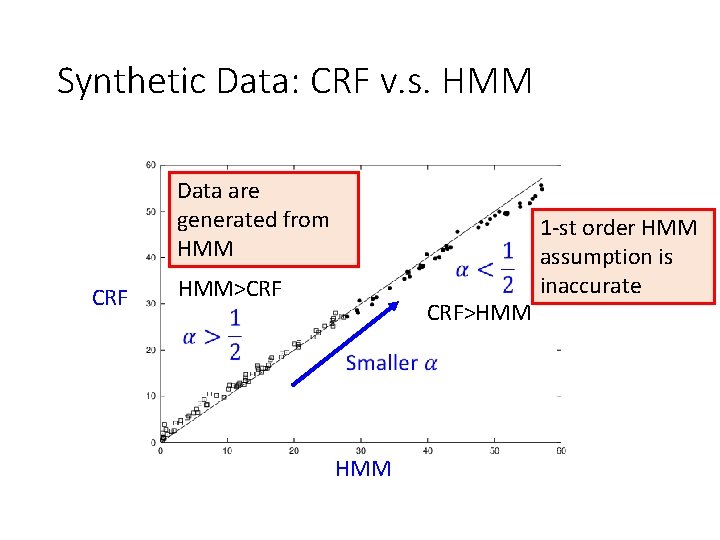
Synthetic Data: CRF v. s. HMM Data are generated from HMM CRF HMM>CRF CRF>HMM 1 -st order HMM assumption is inaccurate
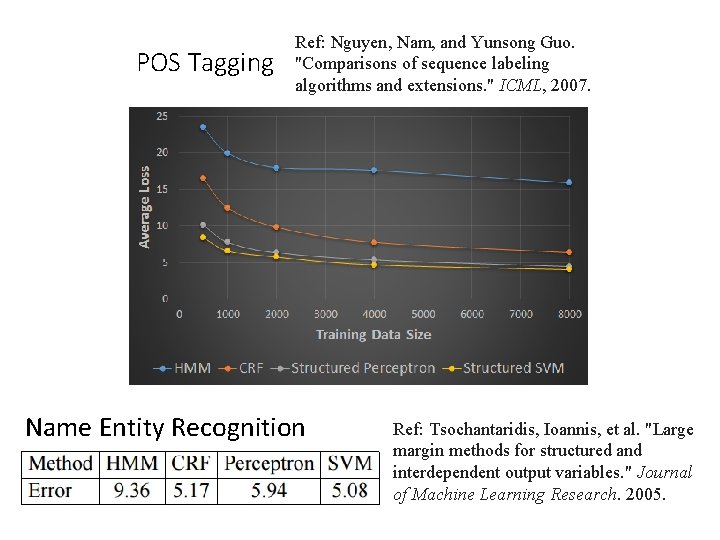
POS Tagging Ref: Nguyen, Nam, and Yunsong Guo. "Comparisons of sequence labeling algorithms and extensions. " ICML, 2007. Name Entity Recognition Ref: Tsochantaridis, Ioannis, et al. "Large margin methods for structured and interdependent output variables. " Journal of Machine Learning Research. 2005.

Concluding Remarks Problem 1 HMM CRF Structured Perceptron Structured SVM Semi. Markov Outlook: RNN, LSTM, CTC Problem 2 Problem 3 Viterbi Just count Viterbi F(x, y) for x and y with Modified different lengths Viterbi Can be the same as CRF, structured perceptron or SVM

Reference • Structured SVM • Tsochantaridis, Ioannis, et al. "Large margin methods for structured and interdependent output variables. " Journal of Machine Learning Research. 2005. • http: //machinelearning. wustl. edu/mlpapers/paper_fi les/Tsochantaridis. JHA 05. pdf • Semi-Markov Model • Sarawagi, Sunita, and William W. Cohen. "Semimarkov conditional random fields for information extraction. " Advances in Neural Information Processing Systems. 2004. • http: //www. cs. cmu. edu/~wcohen/postscript/semi. CR F. pdf

Appendix


Structured SVM – Problem 3: Way 1. Gradient descent: Difficulty: How to compute (not differentiable)
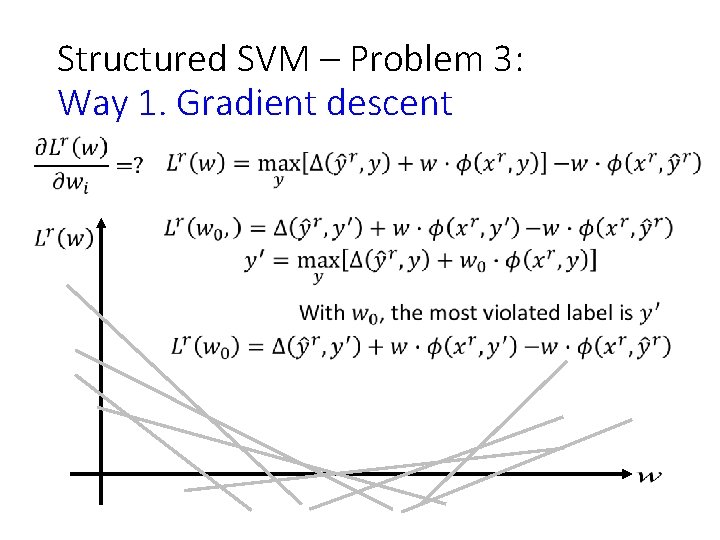
Structured SVM – Problem 3: Way 1. Gradient descent
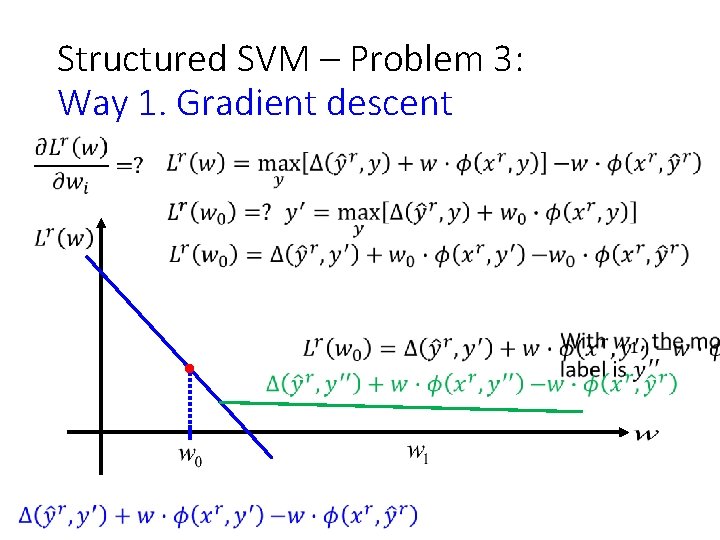
Structured SVM – Problem 3: Way 1. Gradient descent
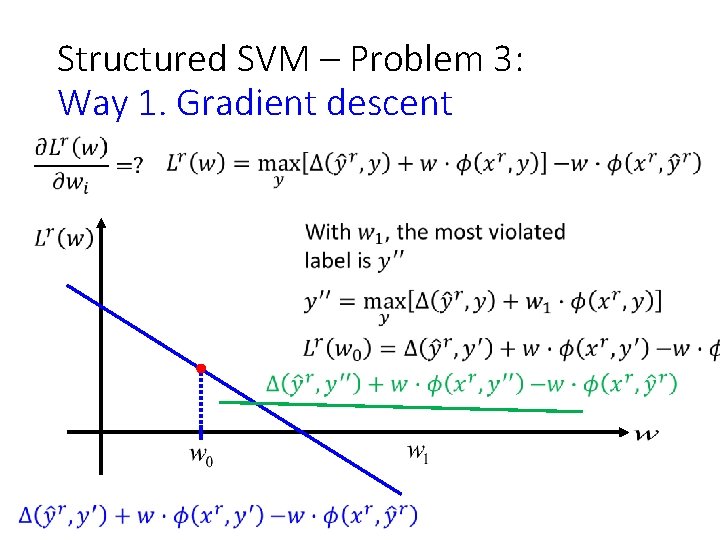
Structured SVM – Problem 3: Way 1. Gradient descent

Structured SVM – Problem 3: Way 1. Gradient descent In each iteration, Assume the weight vector before update is w Around w:

Structured SVM – Problem 3: Way 1. Gradient descent Stochastic version of Structured SVM c. f. Structured Perceptron
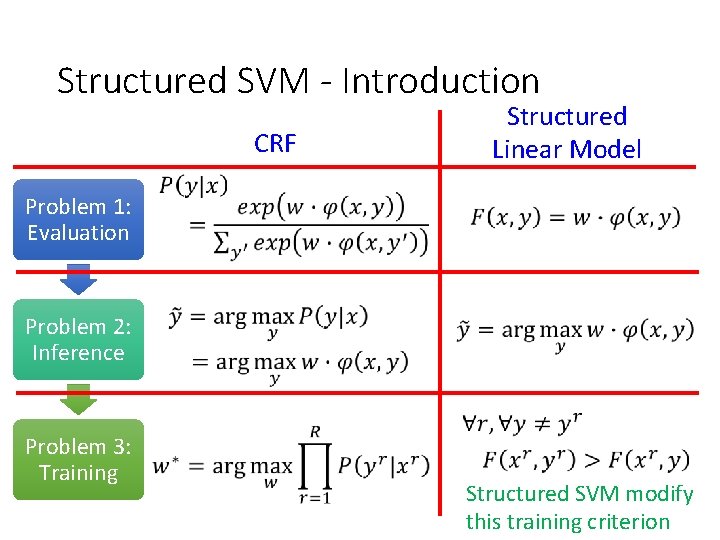
Structured SVM - Introduction CRF Structured Linear Model Problem 1: Evaluation Problem 2: Inference Problem 3: Training Structured SVM modify this training criterion
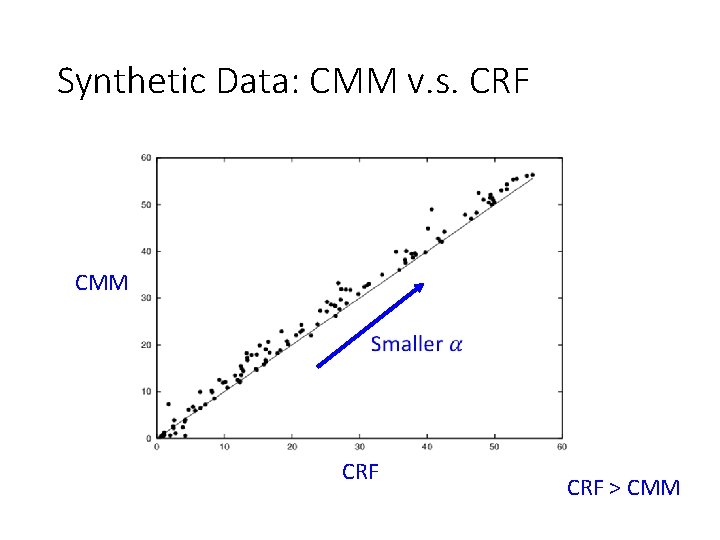
Synthetic Data: CMM v. s. CRF CMM CRF > CMM
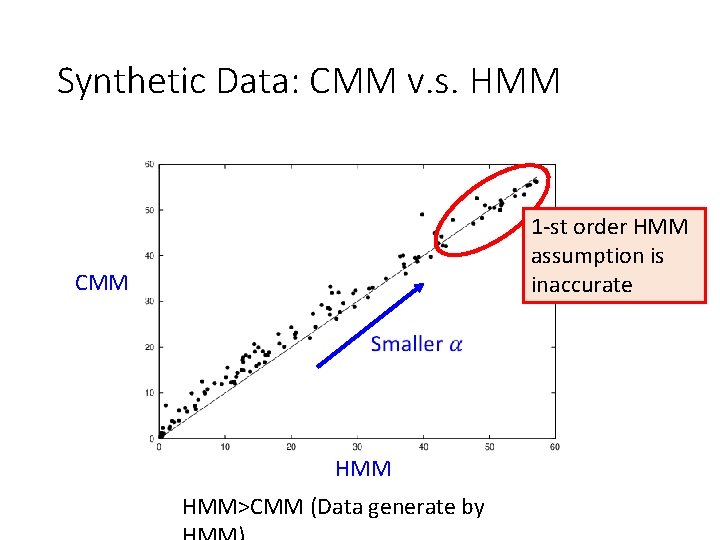
Synthetic Data: CMM v. s. HMM 1 -st order HMM assumption is inaccurate CMM HMM>CMM (Data generate by
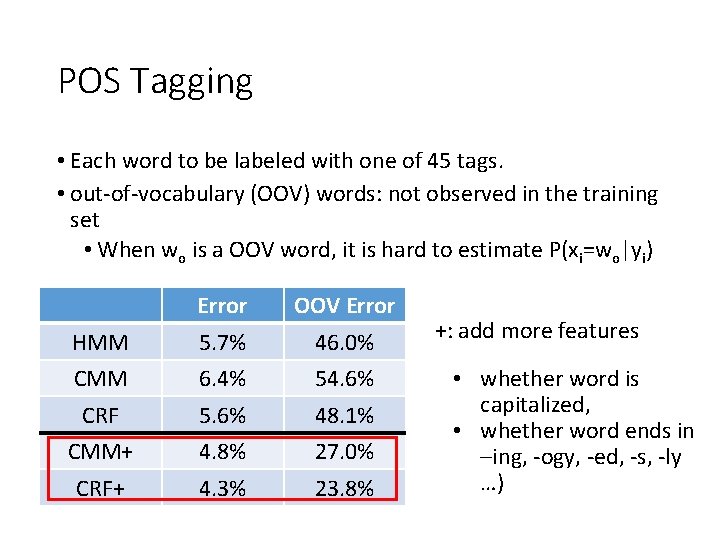
POS Tagging • Each word to be labeled with one of 45 tags. • out-of-vocabulary (OOV) words: not observed in the training set • When wo is a OOV word, it is hard to estimate P(xi=wo|yi) Error OOV Error HMM 5. 7% 46. 0% CMM 6. 4% 54. 6% CRF 5. 6% 48. 1% CMM+ 4. 8% 27. 0% CRF+ 4. 3% 23. 8% +: add more features • whether word is capitalized, • whether word ends in –ing, -ogy, -ed, -s, -ly …)

• http: //dl. acm. org/citation. cfm? id=1102373 • Mappings to structured output spaces (strings, trees, partitions, etc. ) are typically learned using extensions of classification algorithms to simple graphical structures (eg. , linear chains) in which search and parameter estimation can be performed exactly. Unfortunately, in many complex problems, it is rare that exact search or parameter estimation is tractable. Instead of learning exact models and searching via heuristic means, we embrace this difficulty and treat the structured output problem in terms of approximate search. We present a framework for learning as search optimization, and two parameter updates with convergence the-orems and bounds. Empirical evidence shows that our integrated approach to learning and decoding can outperform exact models at smaller computational cost.

• Inference in Conditional Random Fields and Hidden Markov Models is done using the Viterbi algorithm, an efficient dynamic programming algorithm. In many cases, general (non-local and non-sequential) constraints may exist over the output sequence, but cannot be incorporated and exploited in a natural way by this inference procedure. This paper proposes a novel inference procedure based on integer linear programming (ILP) and extends CRF models to naturally and efficiently support general constraint structures. For sequential constraints, this procedure reduces to simple linear programming as the inference process. Experimental evidence is supplied in the context of an important NLP problem, semantic role labeling. • http: //dl. acm. org/citation. cfm? id=1102444

• We present SEARN, an algorithm for integrating SEARch and l. EARNing to solve complex structured prediction problems such as those that occur in natural language, speech, computational biology, and vision. SEARN is a meta-algorithm that transforms these complex problems into simple classification problems to which any binary classifier may be applied. Unlike current algorithms for structured learning that require decomposition of both the loss function and the feature functions over the predicted structure, SEARN is able to learn prediction functions for any loss function and anyclass of features. Moreover, SEARN comes with a strong, natural theoretical guarantee: good performance on the derived classification problems implies good performance on the structured prediction problem. • http: //link. springer. com/article/10. 1007/s 10994 -009 -5106 -x

• For general graphs where we do not want the sub-modularity condition, we can also consider an approximation where we use an approximate decoding method, such as loopy belief propagation or a stochastic local search method [Hutter et al. , 2005]). However, theoretical and empirical work in [Finley and Joachims, 2008] shows that using such under-generating decoding methods (which may return sub-optimal solutions to the decoding problem) have several disadvantages compared to so-called over-generating decoding methods. A typical example of an over-generating decoding method is a linear programming relaxation of an integer programming formulations of decoding, where in the relaxation the objective is optimized exactly over an expanded space [Kumar et al. , 2007], hence yielding a fractional decoding that is a strict upper bound on the optimal decoding.

More for Structured SVM • Margin re-scale v. s. slack rescale • One slack • Cutting plane -> bundle • Ref: • http: //www. machinelearning. org/proceedings/icml 2007/papers/206. pdf • http: //courses. ischool. berkeley. edu/i 290 -dm/s 11/SECURE/gidofalvi. pdf • http: //www. cs. cmu. edu/afs/cs/user/aberger/www/html/tutoria l. html • http: //www. cs. cornell. edu/people/tj/publications/joachims_etal_09 a. pdf • http: //www. cs. ubc. ca/~schmidtm/Documents/2009_Notes_Structured. SVMs. pdf • http: //www. robots. ox. ac. uk/~vedaldi/assets/svm-struct-matlab/tutorial/ssvmtutorial-handout. pdf

SVMs for tagging from Jimenez & Marquez 96
POS Tagging, examples from WSJ From Mc. Callum 97

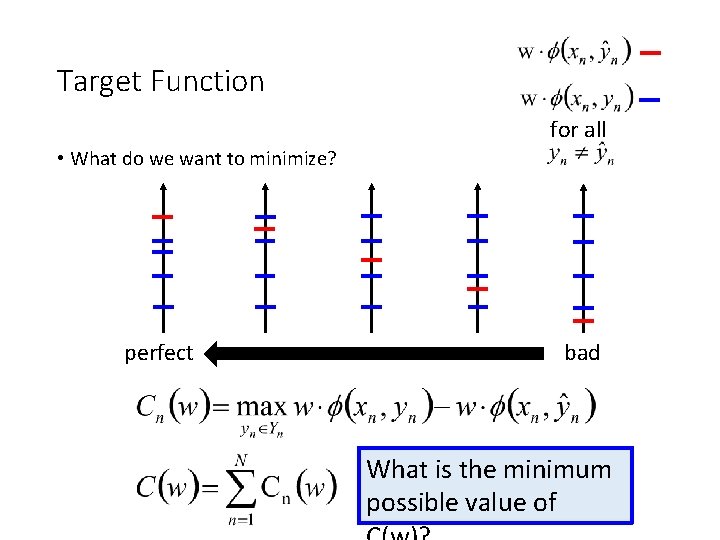
Target Function for all • What do we want to minimize? perfect bad What is the minimum possible value of

Appendix: Viterbi
![HMM - Problem 1 [Slides from Raymond J. Mooney] 0. 05 0. 1 Noun HMM - Problem 1 [Slides from Raymond J. Mooney] 0. 05 0. 1 Noun](http://slidetodoc.com/presentation_image_h2/5dc94ac56552edc6f20c80a75b4cb4fb/image-101.jpg)
HMM - Problem 1 [Slides from Raymond J. Mooney] 0. 05 0. 1 Noun Det 0. 5 0. 9 Verb 0. 05 0. 1 0. 4 0. 25 Prop. Noun 0. 8 0. 1 0. 5 start 0. 1 stop 0. 25 P(y = “Prop. Noun Verb Det Noun”) = 0. 4*0. 8*0. 25*0. 95*0. 1
![HMM - Problem 1 [Slides from Raymond J. Mooney] y = “Prop. Noun Verb HMM - Problem 1 [Slides from Raymond J. Mooney] y = “Prop. Noun Verb](http://slidetodoc.com/presentation_image_h2/5dc94ac56552edc6f20c80a75b4cb4fb/image-102.jpg)
HMM - Problem 1 [Slides from Raymond J. Mooney] y = “Prop. Noun Verb Det Noun” P(y) = 0. 4*0. 8*0. 25*0. 95*0. 1 Tom John Mary Alice Jerry bit ate saw played hit gave the a the that cat dog saw bed pen apple Prop. Noun Verb Det Noun John saw the saw P(John|Prop. Noun) = 1/5

HMM - Problem 2: Viterbi Algorithm

HMM: Problem 2 – Viterbi Algorithm xk xk+1 P P V V D D N N …… ……

HMM: Problem 2 – Viterbi Algorithm s is a possible tag (e. g. N, V ……)
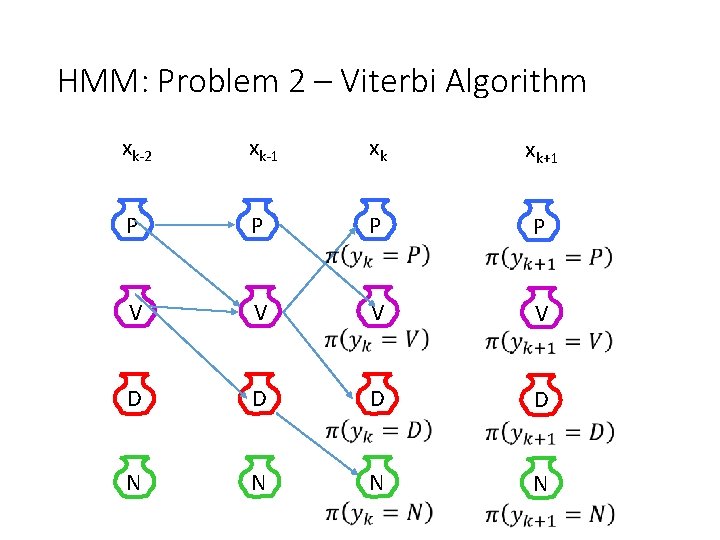
HMM: Problem 2 – Viterbi Algorithm xk-2 xk-1 xk xk+1 P P V V D D N N
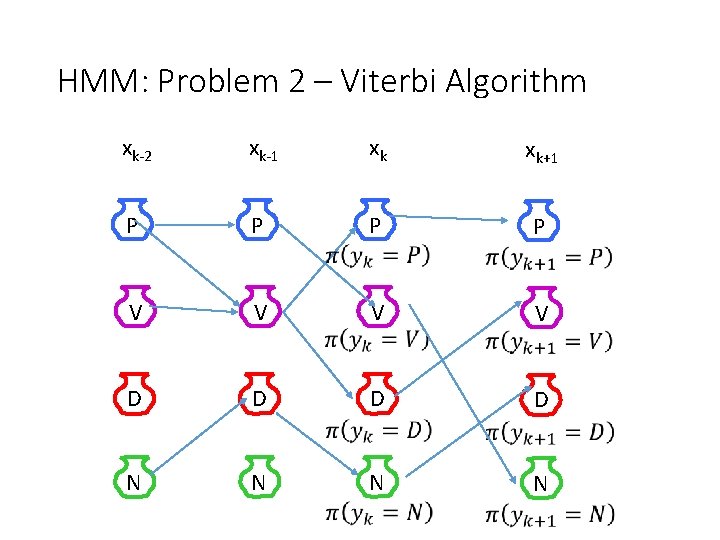
HMM: Problem 2 – Viterbi Algorithm xk-2 xk-1 xk xk+1 P P V V D D N N
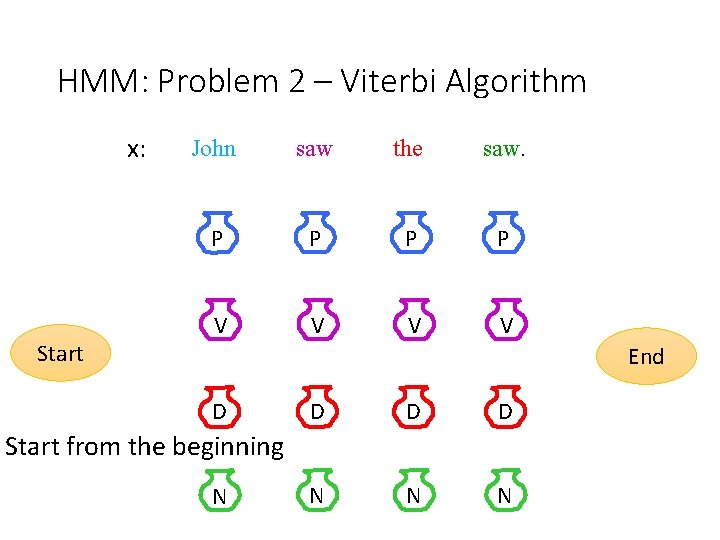
HMM: Problem 2 – Viterbi Algorithm x: Start John saw the saw. P P V V End D D N N N Start from the beginning N
- Slides: 108