Structure Learning Overview l l l Structure learning

Structure Learning

Overview l l l Structure learning Predicate invention Transfer learning

Structure Learning l Can learn MLN structure in two separate steps: l l Learn first-order clauses with an off-the-shelf ILP system (e. g. , CLAUDIEN) Learn clause weights by optimizing (pseudo) likelihood Unlikely to give best results because ILP optimizes accuracy/frequency, not likelihood Better: Optimize likelihood during search 3

Structure Learning Algorithm l High-level algorithm REPEAT MLN Ã MLN [ Find. Best. Clauses(MLN) UNTIL Find. Best. Clauses(MLN) returns NULL l Find. Best. Clauses(MLN) Create candidate clauses FOR EACH candidate clause c Compute increase in evaluation measure of adding c to MLN RETURN k clauses with greatest increase 4

Structure Learning l l Evaluation measure Clause construction operators Search strategies Speedup techniques 5

Evaluation Measure l Fastest: Pseudo-log-likelihood l l This gives undue weight to predicates with large # of groundings 6

Evaluation Measure l Weighted pseudo-log-likelihood (WPLL) l Gaussian weight prior l Structure prior l 7

Evaluation Measure l Weighted pseudo-log-likelihood (WPLL) l weight given to predicate r Gaussian weight prior l Structure prior l 8

Evaluation Measure l Weighted pseudo-log-likelihood (WPLL) l weight given to predicate r sums over groundings of predicate r Gaussian weight prior l Structure prior l 9

Evaluation Measure l Weighted pseudo-log-likelihood (WPLL) l weight given to predicate r CLL: conditional log-likelihood sums over groundings of predicate r Gaussian weight prior l Structure prior l 10

Clause Construction Operators l l Add a literal (negative or positive) Remove a literal Flip sign of literal Limit number of distinct variables to restrict search space 11

Beam Search l l Same as that used in ILP & rule induction Repeatedly find the single best clause 12

Shortest-First Search (SFS) 1. 2. 3. 4. l Start from empty or hand-coded MLN FOR L Ã 1 TO MAX_LENGTH Apply each literal addition & deletion to each clause to create clauses of length L Repeatedly add K best clauses of length L to the MLN until no clause of length L improves WPLL Similar to Della Pietra et al. (1997), Mc. Callum (2003) 13

Speedup Techniques l Find. Best. Clauses(MLN) Creates candidate clauses FOR EACH candidate clause c Compute increase in WPLL (using L-BFGS) of adding c to MLN RETURN k clauses with greatest increase 14

Speedup Techniques l Find. Best. Clauses(MLN) Creates candidate clauses FOR EACH candidate clause c Compute increase in WPLL (using L-BFGS) of adding c to MLN RETURN k clauses with greatest increase SLOW Many candidates 15

Speedup Techniques l Find. Best. Clauses(MLN) Creates candidate clauses FOR EACH candidate clause c Compute increase in WPLL (using L-BFGS) of adding c to MLN RETURN k clauses with greatest increase SLOW Many candidates SLOW Many CLLs SLOW Each CLL involves a #P-complete problem 16

Speedup Techniques l Find. Best. Clauses(MLN) Creates candidate clauses FOR EACH candidate clause c Compute increase in WPLL (using L-BFGS) of adding c to MLN RETURN k clauses with greatest increase NOT THAT FAST SLOW Many candidates SLOW Many CLLs SLOW Each CLL involves a #P-complete problem 17

Speedup Techniques l l l Clause sampling Predicate sampling Avoid redundant computations Loose convergence thresholds Weight thresholding 18

Overview l l l Structure learning Predicate invention Transfer learning

Motivation Statistical Relational Learning Statistical Learning Relational Learning (ILP) • able to handle noisy data • able to handle non-i. i. d. data

Motivation Statistical Predicate Invention Discovery of new concepts, properties, and relations Statistical Relational Learning from data Latent Statistical Variable Learning Discovery Predicate Invention Relational Learning (ILP) [Elidan & Friedman, 2005; Elidandata et al. , 2001; etc. ] • able to handle noisy [Wogulis & Langley, Muggleton • able to handle 1989; non-i. i. d. data & Buntine, 1988; etc. ]

Benefits of Predicate Invention l l l More compact and comprehensible models Improve accuracy by representing unobserved aspects of domain Model more complex phenomena

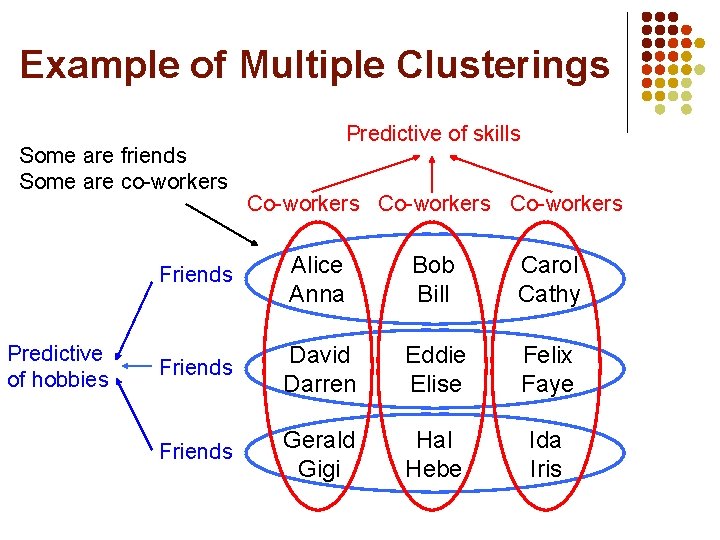
Multiple Relational Clusterings l l l l Clusters objects and relations simultaneously Multiple types of objects Relations can be of any arity #Clusters need not be specified in advance Learns multiple cross-cutting clusterings Finite second-order Markov logic First step towards general framework for SPI

Multiple Relational Clusterings l l l Invent unary predicate = Cluster Multiple cross-cutting clusterings Cluster relations by objects they relate and vice versa Cluster objects of same type Cluster relations with same arity and argument types

Example of Multiple Clusterings Some are friends Some are co-workers Predictive of hobbies Predictive of skills Co-workers Friends Alice Anna Bob Bill Carol Cathy Friends David Darren Eddie Elise Felix Faye Friends Gerald Gigi Hal Hebe Ida Iris

Second-Order Markov Logic l l l Finite, function-free Variables range over relations (predicates) and objects (constants) Ground atoms with all possible predicate symbols and constant symbols Represent some models more compactly than first-order Markov logic Specify how predicate symbols are clustered

Symbols l Cluster: Clustering: Atom: l Cluster combination: l l ,

MRC Rules l Each symbol belongs to at least one cluster l Symbol cannot belong to >1 cluster in same clustering l Each atom appears in exactly one combination of clusters

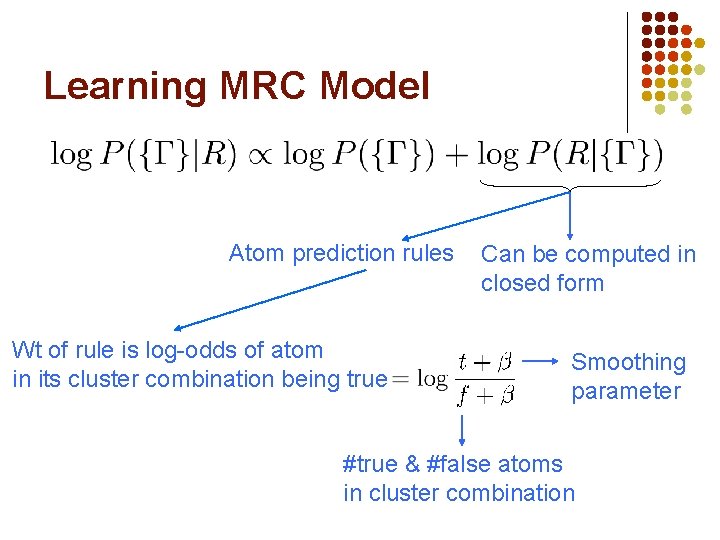
MRC Rules l Atom prediction rule: Truth value of atom is determined by cluster combination it belongs to l Exponential prior on number of clusters

Learning MRC Model Learning consists of finding l l Cluster assignment { }: assignment of truth values to and atoms Weights of atom prediction rules that maximize log-posterior probability Vector of truth assignments to all observed ground atoms all

Learning MRC Model Three hard rules + Exponential prior rule

Learning MRC Model Atom prediction rules Wt of rule is log-odds of atom in its cluster combination being true Can be computed in closed form Smoothing parameter #true & #false atoms in cluster combination

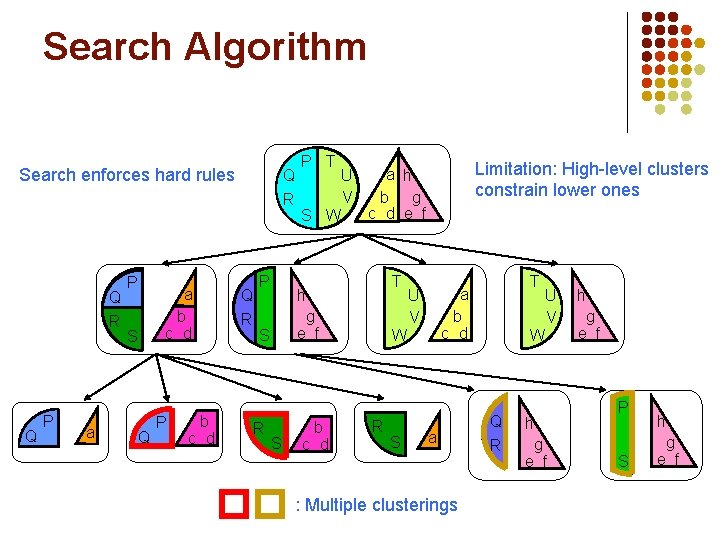
Search Algorithm l l Approximation: Hard assignment of symbols to clusters Greedy with restarts Top-down divisive refinement algorithm Two levels l l Top-level finds clusterings Bottom-level finds clusters

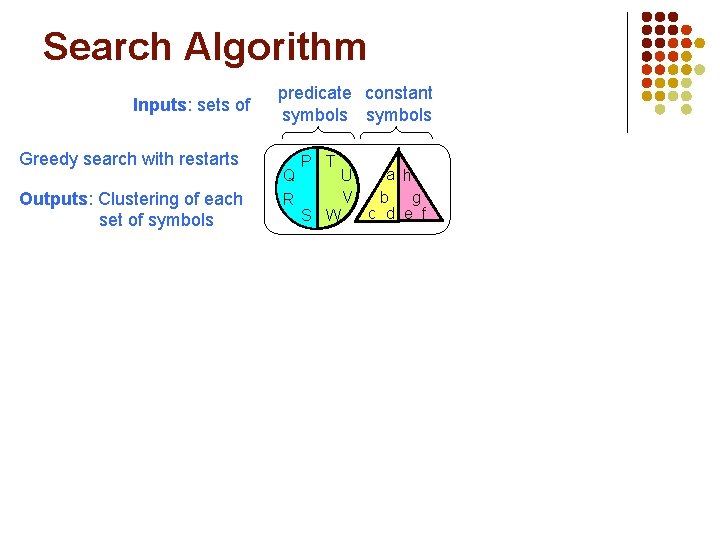
Search Algorithm Inputs: sets of Greedy search with restarts Outputs: Clustering of each set of symbols predicate constant symbols Q R P T S W U V a h b g c d e f

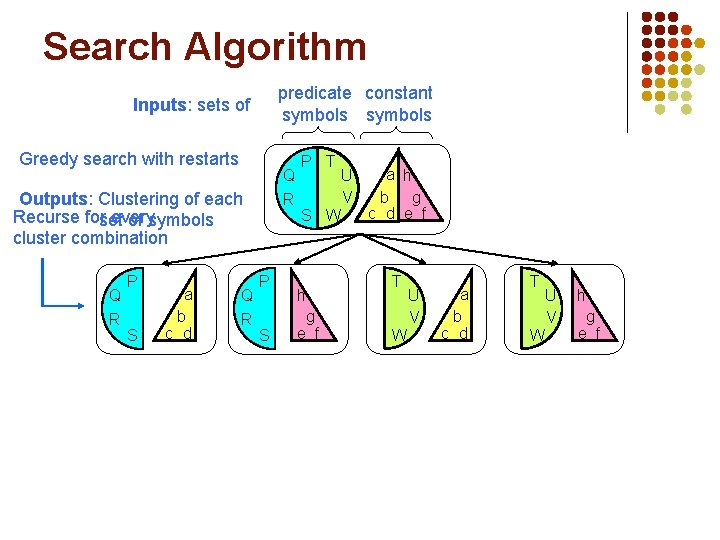
Search Algorithm predicate constant symbols Inputs: sets of Greedy search with restarts Q R Outputs: Clustering of each Recurse forset every of symbols cluster combination Q R P S a b c d Q R P S P T S W h g e f U V a h b g c d e f T W U V a b c d T W U V h g e f

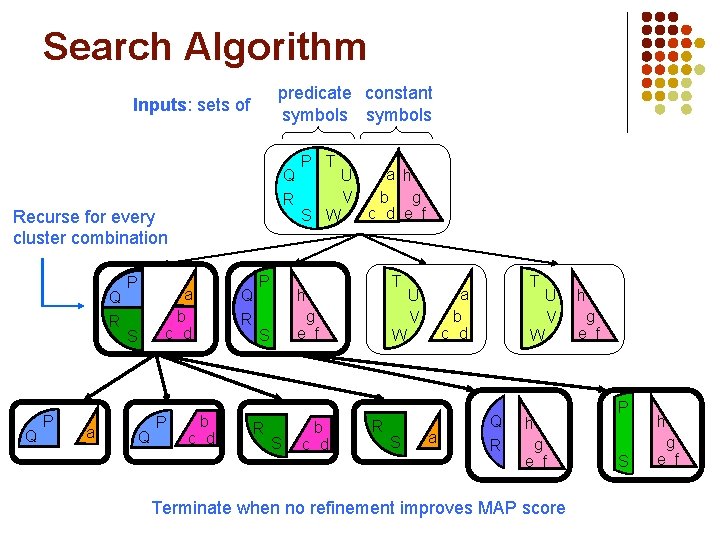
Search Algorithm predicate constant symbols Inputs: sets of Q R Recurse for every cluster combination Q R Q P a b c d S Q P b c d Q R P S W U V a h b g c d e f T h g e f S R P T S b c d U V W R S T a b c d a U V W Q R h g e f Terminate when no refinement improves MAP score h g e f P S h g e f

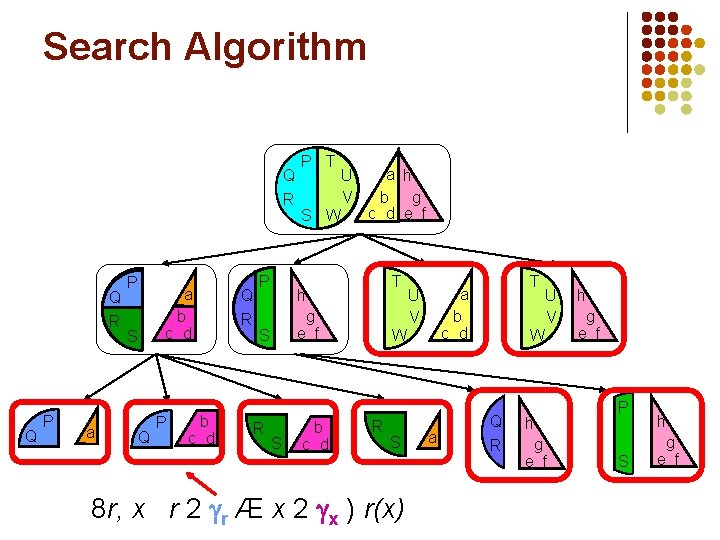
Search Algorithm Q R Q P a b c d S Q 8 r, x P b c d Q R P S W U V a h b g c d e f T h g e f S R P T S b c d U V W R S Leaf ≡ atom prediction rule r 2 leaves Return r Æ x 2 x ) r(x) T a b c d a U V W Q R h g e f P S h g e f

Search Algorithm Search enforces hard rules Q R Q P a b c d S Q P b c d Q R P S W U V T g e f S b c d Limitation: High-level clusters constrain lower ones a h b g c d e f h S R P T U V W R S T a b c d a : Multiple clusterings U V W Q R h g e f P S h g e f

Overview l l l Structure learning Predicate invention Transfer learning

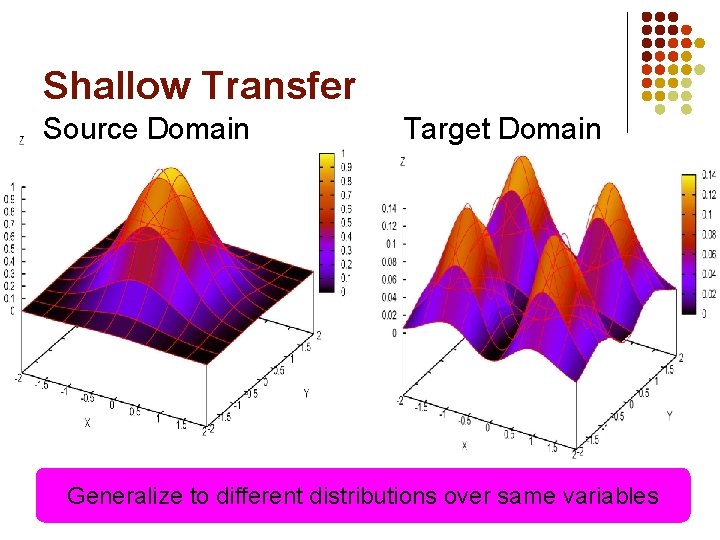
Shallow Transfer Source Domain Target Domain Generalize to different distributions over same variables

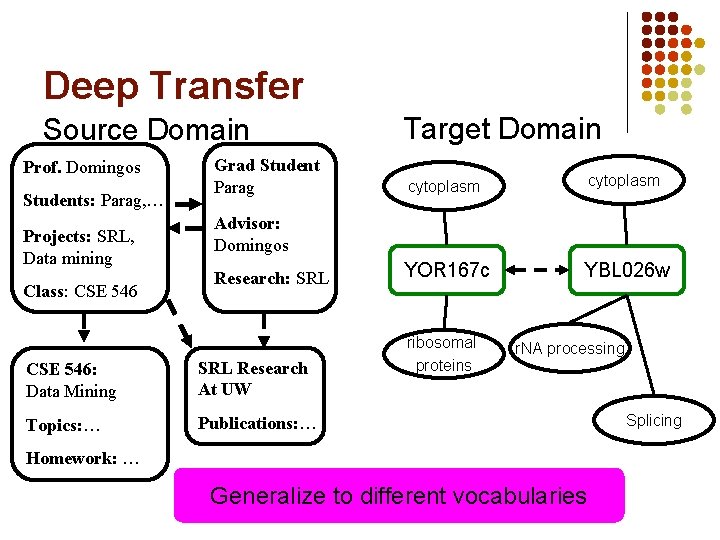
Deep Transfer Source Domain Prof. Domingos Students: Parag, … Projects: SRL, Data mining Class: CSE 546 Grad Student Parag Target Domain cytoplasm YOR 167 c YBL 026 w Advisor: Domingos Research: SRL CSE 546: Data Mining SRL Research At UW Topics: … Publications: … ribosomal proteins r. NA processing Homework: … Generalize to different vocabularies Splicing

Deep Transfer via Markov Logic (DTM) l Clique templates l l Abstract away predicate names Discern high-level structural regularities l Check if each template captures a regularity beyond sub-clique templates l Transferred knowledge provides declarative bias in target domain

Transfer as Declarative Bias l l Large search space of first-order clauses → Declarative bias is crucial Limit search space l l Maximum clause length Type constraints l Background knowledge l DTM discovers declarative bias in one domain and applies it in another

Intuition Behind DTM Have the same second order structure: 1) Map Location and Complex to r 2) Map Interacts to s

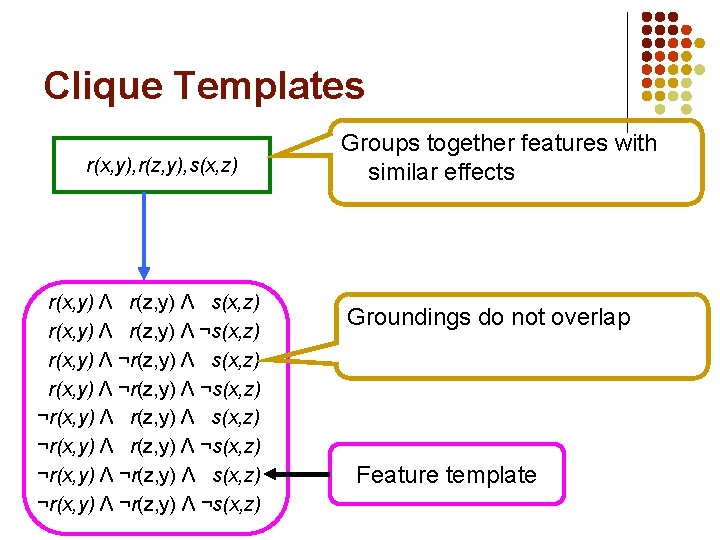
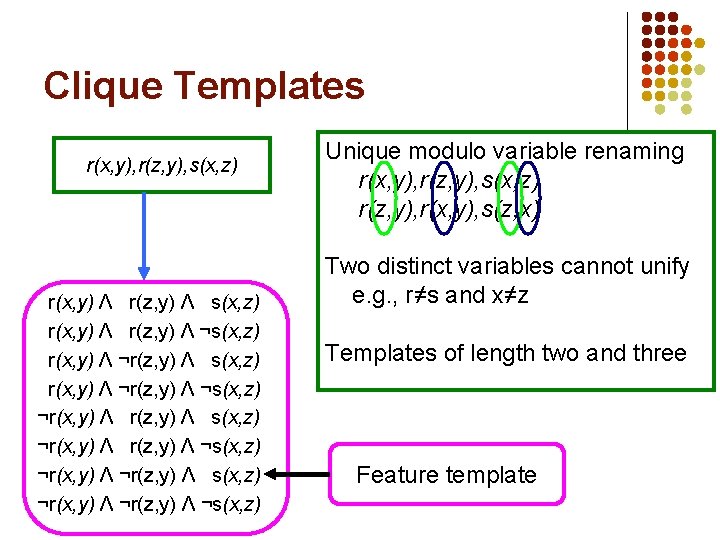
Clique Templates r(x, y), r(z, y), s(x, z) r(x, y) Λ r(z, y) Λ ¬s(x, z) r(x, y) Λ ¬r(z, y) Λ ¬s(x, z) ¬r(x, y) Λ ¬r(z, y) Λ ¬s(x, z) Groups together features with similar effects Groundings do not overlap Feature template

Clique Templates r(x, y), r(z, y), s(x, z) r(x, y) Λ r(z, y) Λ ¬s(x, z) r(x, y) Λ ¬r(z, y) Λ ¬s(x, z) ¬r(x, y) Λ ¬r(z, y) Λ ¬s(x, z) Unique modulo variable renaming r(x, y), r(z, y), s(x, z) r(z, y), r(x, y), s(z, x) Two distinct variables cannot unify e. g. , r≠s and x≠z Templates of length two and three Feature template

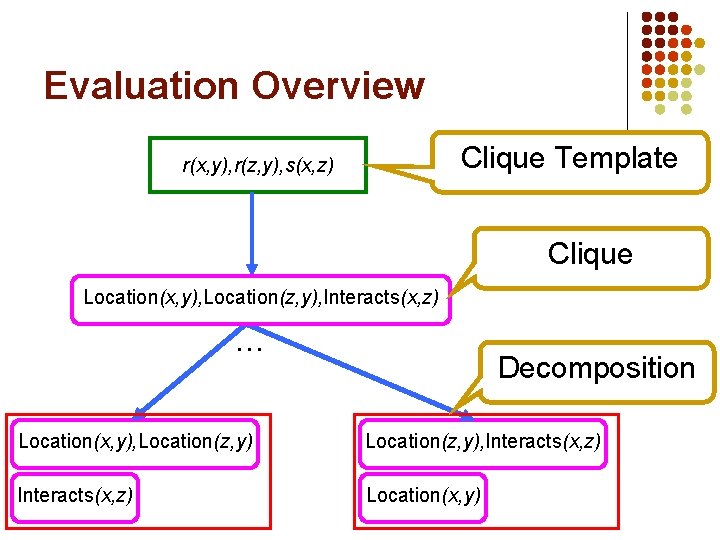
Evaluation Overview Clique Template r(x, y), r(z, y), s(x, z) Clique Location(x, y), Location(z, y), Interacts(x, z) … Decomposition Location(x, y), Location(z, y), Interacts(x, z) Location(x, y)

Clique Evaluation Location(x, y), Location(z, y), Interacts(x, z) Q: Does the clique capture … a regularity beyond its sub-cliques? Prob(Location(x, y), Location(z, y), Interacts(x, z)) ≠ Prob(Location(x, y), Location(z, y)) x Prob(Interacts(x, z)) … Location(x, y), Location(z, y), Interacts(x, z) Prob(Location(x, y), Location(z, y), Interacts(x, z)) ≠ Interacts(x, z) Location(x, y) Prob(Location(x, y), Location(z, y)) x Prob(Interacts(x, z))

Scoring a Decomposition l KL divergence l p is clique´s probability distribution q is distribution predicted by decomposition l

Clique Score Location(x, y), Location(z, y), Interacts(x, z) Score: 0. 02 Min over scores Score: 0. 04 Score: 0. 02 Location(x, y), Location(z, y), Interacts(x, z) Location(x, y) Score: 0. 02 Location(x, y), Interacts(x, z) Location(z, y)

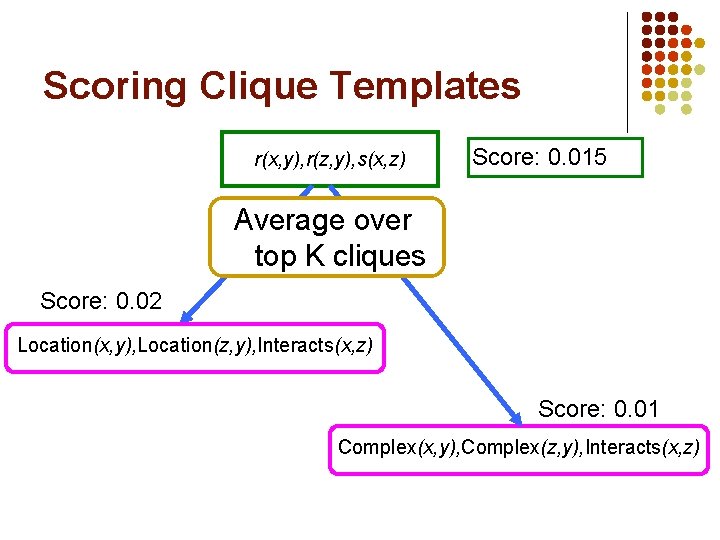
Scoring Clique Templates r(x, y), r(z, y), s(x, z) Score: 0. 015 … Average over top K cliques Score: 0. 02 Location(x, y), Location(z, y), Interacts(x, z) Score: 0. 01 Complex(x, y), Complex(z, y), Interacts(x, z)

Transferring Knowledge

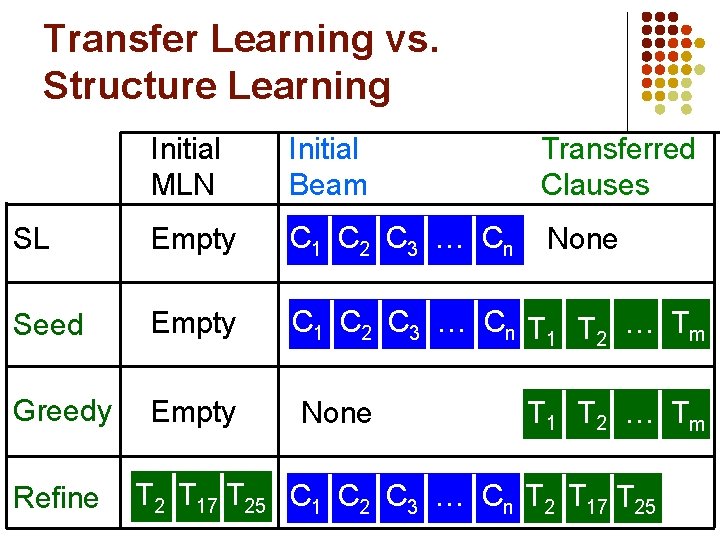
Using Transferred Knowledge l l Influence structure learning in target domain Markov logic structure learning (MSL) [Kok & Domingos, 2005] l l Start with unit clauses Modify clauses by adding, deleting, negating literals in clause Score by weighted-pseudo log likelihood Beam search

Transfer Learning vs. Structure Learning Initial MLN Initial Beam Transferred Clauses SL Empty C 1 C 2 C 3 … Cn None Seed Empty C 1 C 2 C 3 … Cn TT … TTmm. Tm 1 1 T… 2 1 T Greedy Empty Refine None T 1 T 2 … Tm T 2 T 17 T 25 C 1 C 2 C 3 … Cn T 2 T 17 T 25

Extensions of Markov Logic l l Continuous domains Infinite domains Recursive Markov logic Relational decision theory