Structure from Motion Structure from Motion For now

Structure from Motion

Structure from Motion • For now, static scene and moving camera – Equivalently, rigidly moving scene and static camera • Limiting case of stereo with many cameras • Limiting case of multiview camera calibration with unknown target • Given n points and N camera positions, have 2 n. N equations and 3 n+6 N unknowns

Approaches • Obtaining point correspondences – Optical flow – Stereo methods: correlation, feature matching • Solving for points and camera motion – Nonlinear minimization (bundle adjustment) – Various approximations…

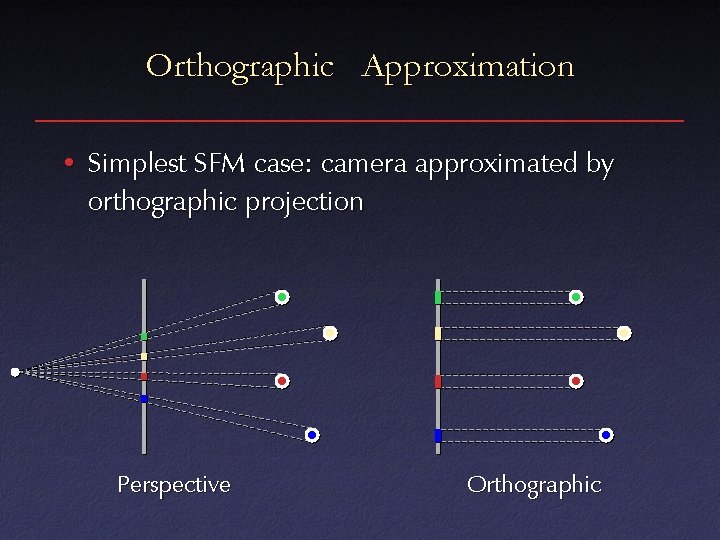
Orthographic Approximation • Simplest SFM case: camera approximated by orthographic projection Perspective Orthographic

Weak Perspective • An orthographic assumption is sometimes well approximated by a telephoto lens Weak Perspective

Consequences of Orthographic Projection • Scene can be recovered up to scale • Translation perpendicular to image plane can never be recovered

Orthographic Structure from Motion • Method due to Tomasi & Kanade, 1992 • Assume n points in space p 1 … pn • Observed at N points in time at image coordinates (x ij, yij), i = 1: N, j=1: n – Feature tracking, optical flow, etc.

Orthographic Structure from Motion • Write down matrix of data Points Frames

Orthographic Structure from Motion • Step 1: find translation • Translation parallel to viewing direction can not be obtained • Translation perpendicular to viewing direction equals motion of average position of all points

Orthographic Structure from Motion • Subtract average of each row

Orthographic Structure from Motion • Step 2: try to find rotation • Rotation at each frame defines local coordinate axes , , and • Then

Orthographic Structure from Motion • So, can write where R is a “rotation” matrix and S is a “shape” matrix

Orthographic Structure from Motion • Goal is to factor • Before we do, observe that rank ( (in ideal case with no noise) )=3 • Proof: – Rank of R is 3 unless no rotation – Rank of S is 3 iff have noncoplanar points – Product of 2 matrices of rank 3 has rank 3 • With noise, rank ( ) might be > 3

SVD • Goal is to factor into R and S • Apply SVD: • But should have rank 3 all but 3 of the wi should be 0 • Extract the top 3 wi, together with the corresponding columns of U and V

Factoring for Orthographic Structure from Motion • After extracting columns, U 3 has dimensions 2 N 3 (just what we wanted for R) • W 3 V 3 T has dimensions 3 n (just what we wanted for S) • So, let R*=U 3, S*=W 3 V 3 T

Affine Structure from Motion • The i and j entries of R* are not, in general, unit length and perpendicular • We have found motion (and therefore shape) up to an affine transformation • This is the best we could do if we didn’t assume orthographic camera

Ensuring Orthogonality • Since can be factored as R* S*, it can also be factored as (R*Q)(Q-1 S*), for any Q • So, search for Q such that R = R* Q has the properties we want

Ensuring Orthogonality • Want or • Let T = QQT • Equations for elements of T – solve by least squares • Ambiguity – add constraints

Ensuring Orthogonality • Have found T = QQT • Find Q by taking “square root” of T – Cholesky decomposition if T is positive definite – General algorithms (e. g. sqrtm in Matlab)

Orthogonal Structure from Motion • Let’s recap: – – – Write down matrix of observations Find translation from avg. position Subtract translation Factor matrix using SVD Write down equations for orthogonalization Solve using least squares, square root • At end, get matrix R = R* Q of camera positions and matrix S = Q-1 S* of 3 D points

Results • Image sequence [Tomasi & Kanade]

Results • Tracked features [Tomasi & Kanade]

Results • Reconstructed shape Top view Front view [Tomasi & Kanade]

Orthographic Perspective • With orthographic or “weak perspective” can’t recover all information • With full perspective, can recover more information (translation along optical axis) • Result: can recover geometry and full motion up to global scale factor

Perspective SFM Methods • Bundle adjustment (full nonlinear minimization) • Methods based on factorization • Methods based on fundamental matrices • Methods based on vanishing points

Motion Field for Camera Motion • Translation: • Motion field lines converge (possibly at )

Motion Field for Camera Motion • Rotation: • Motion field lines do not converge

Motion Field for Camera Motion • Combined rotation and translation: motion field lines have component that converges, and component that does not • Algorithms can look for vanishing point, then determine component of motion around this point • “Focus of expansion / contraction” • “Instantaneous epipole”

Finding Instantaneous Epipole • Observation: motion field due to translation depends on depth of points • Motion field due to rotation does not • Idea: compute difference between motion of a point, motion of neighbors • Differences should point towards instantaneous epipole

SVD (Again!) • Want to fit direction to all v (differences in optical flow) within some neighborhood • PCA on matrix of v • Equivalently, take eigenvector of A = ( v)T corresponding to largest eigenvalue • Gives direction of parallax li in that patch, together with estimate of reliability

SFM Algorithm • Compute optical flow • Find vanishing point (least squares solution) • Find direction of translation from epipole • Find perpendicular component of motion • Find velocity, axis of rotation • Find depths of points (up to global scale)