STRUCTURE FORMATION MATTEO VIEL INAF and INFN Trieste

STRUCTURE FORMATION MATTEO VIEL INAF and INFN Trieste SISSA LECTURE nr 6 - 15 th March 2011

OUTLINE: LECTURES 1. Structure formation: tools and the high redshift universe 2. The dark ages and the universe at 21 cm 3. IGM cosmology at z=2=6 4. IGM astrophysics at z=2 -6 5. Cosmological probes LCDM scenario 6. Review of main concepts

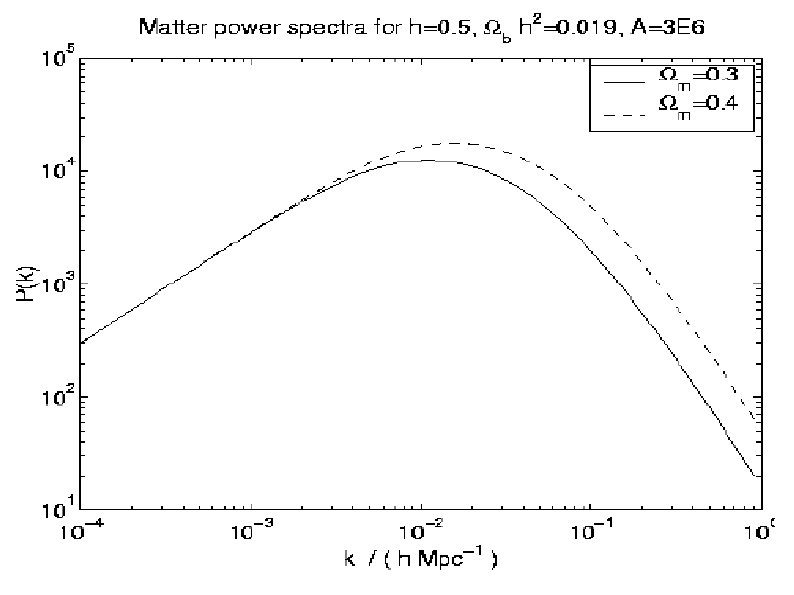
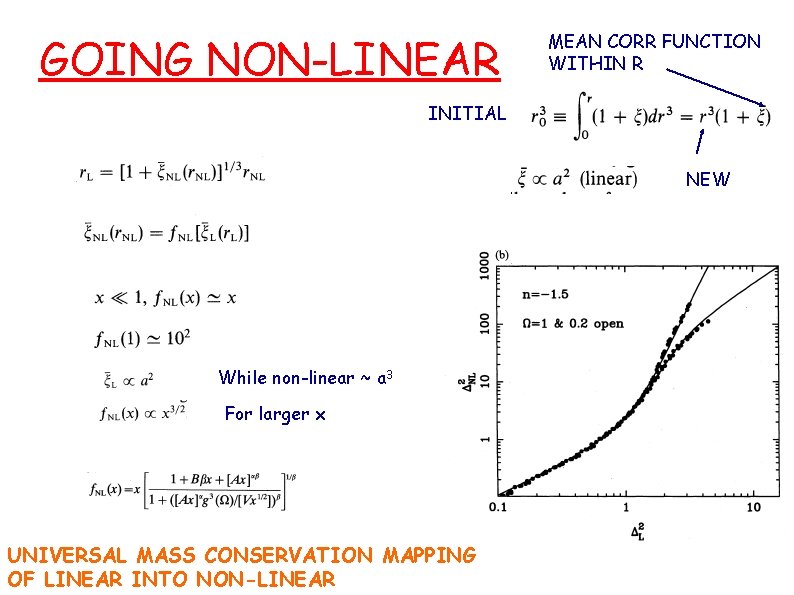
GOING NON-LINEAR MEAN CORR FUNCTION WITHIN R INITIAL NEW While non-linear ~ a 3 For larger x UNIVERSAL MASS CONSERVATION MAPPING OF LINEAR INTO NON-LINEAR

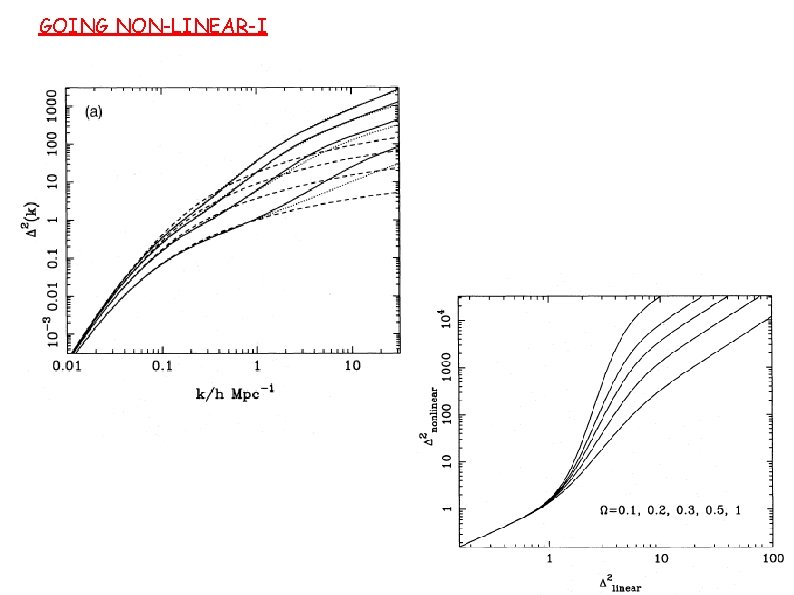
GOING NON-LINEAR-I

COSMIC EXPANSION

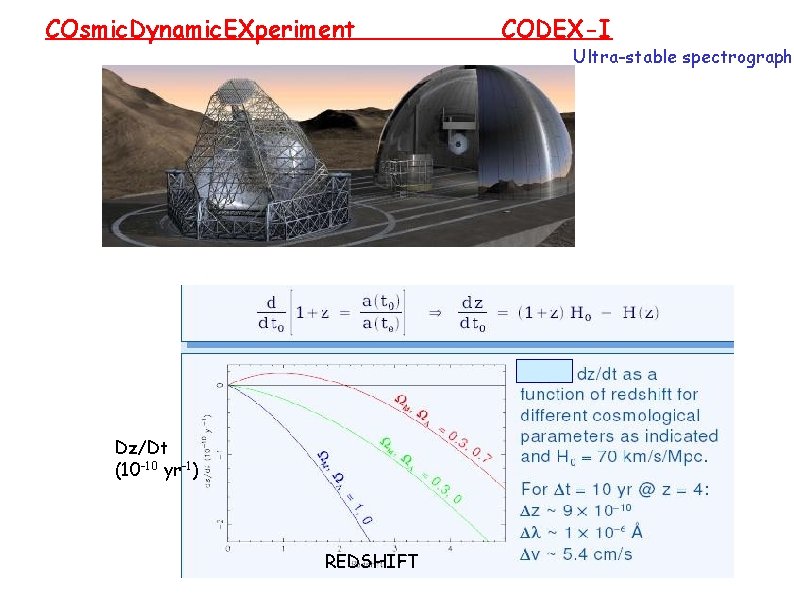
Measuring the cosmic expansion? This is a fundamental quantity not related at all to the FRW equations! If you want to do such a thing then…

COsmic. Dynamic. EXperiment Dz/Dt (10 -10 yr-1) REDSHIFT CODEX-I Ultra-stable spectrograph

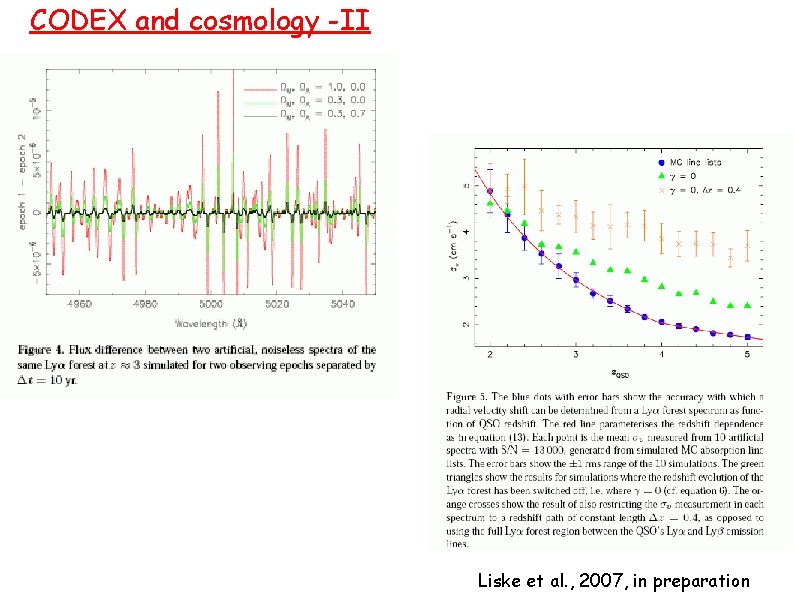
CODEX and cosmology -II Liske et al. , 2007, in preparation

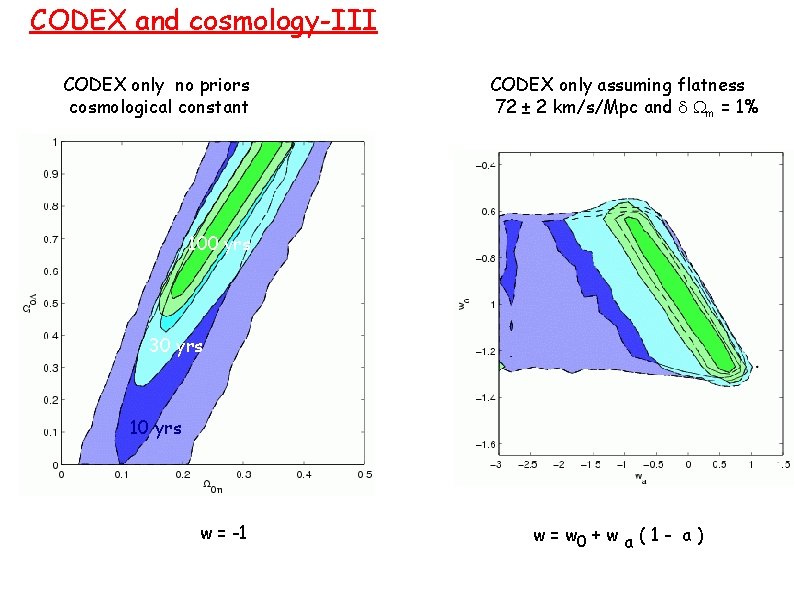
CODEX and cosmology-III CODEX only no priors cosmological constant CODEX only assuming flatness 72 ± 2 km/s/Mpc and d Wm = 1% 100 yrs 30 yrs 10 yrs w = -1 w = w 0 + w a ( 1 - a )

NON – LINEAR EVOLUTION OF COSMIC STRUCTURE

LECTURE # 1 Neutralino DM

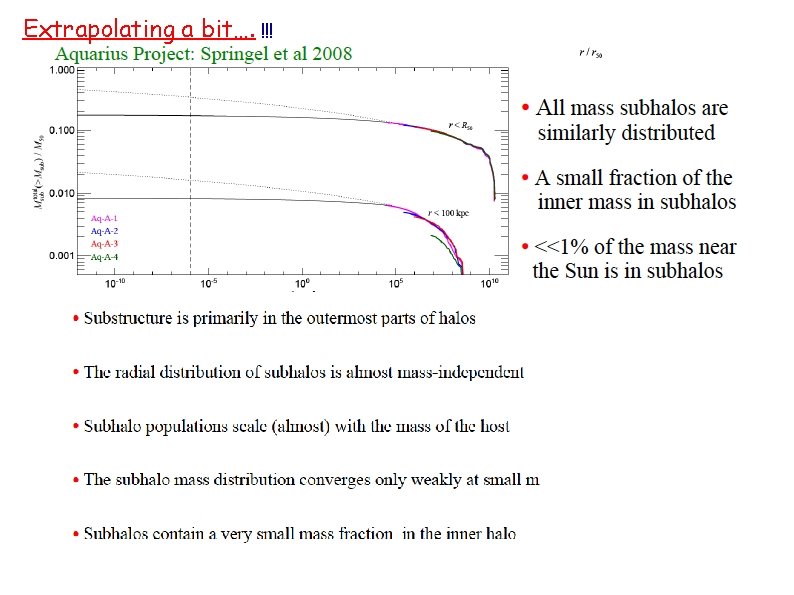
Extrapolating a bit…. !!!

LECTURE # 2 21 cm cosmic structures

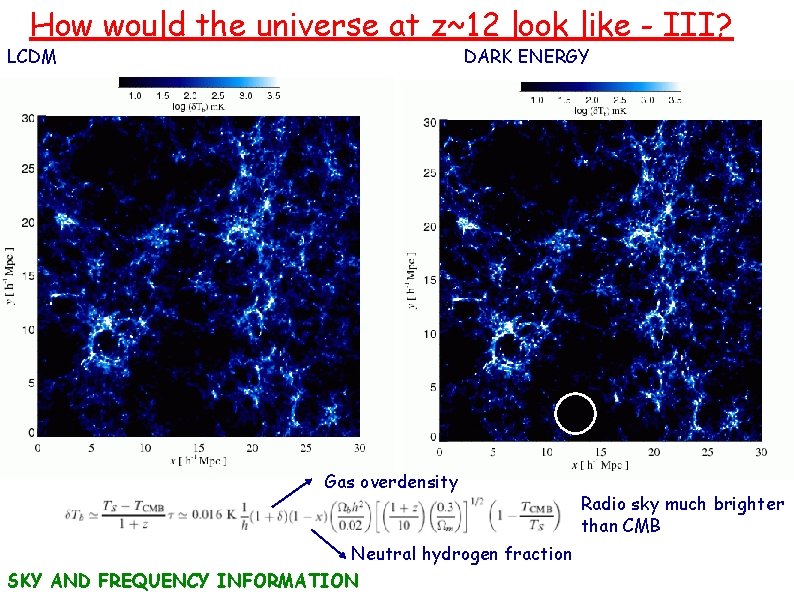
How would the universe at z~12 look like - III? LCDM DARK ENERGY Gas overdensity Neutral hydrogen fraction SKY AND FREQUENCY INFORMATION Radio sky much brighter than CMB

LECTURE # 3 NEUTRINOS and LYMAN-a

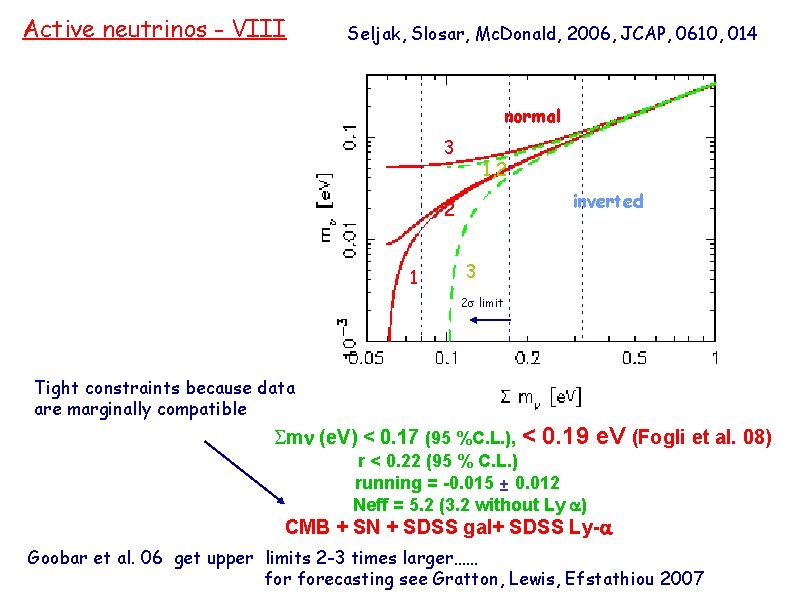
Active neutrinos - VIII Seljak, Slosar, Mc. Donald, 2006, JCAP, 0610, 014 normal 3 1, 2 inverted 2 1 3 2 s limit Tight constraints because data are marginally compatible Smn (e. V) < 0. 17 (95 %C. L. ), < 0. 19 e. V (Fogli et al. 08) r < 0. 22 (95 % C. L. ) running = -0. 015 ± 0. 012 Neff = 5. 2 (3. 2 without Ly a) CMB + SN + SDSS gal+ SDSS Ly-a Goobar et al. 06 get upper limits 2 -3 times larger…… forecasting see Gratton, Lewis, Efstathiou 2007

LECTURE # 4 FEEDBACK FROM GALACTIC WINDS

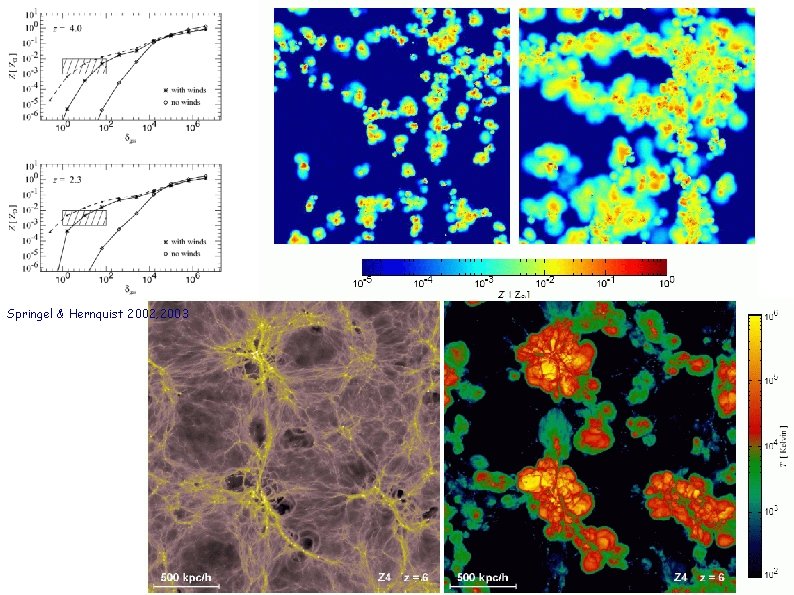
Springel & Hernquist 2002, 2003

LECTURE # 5 BAO

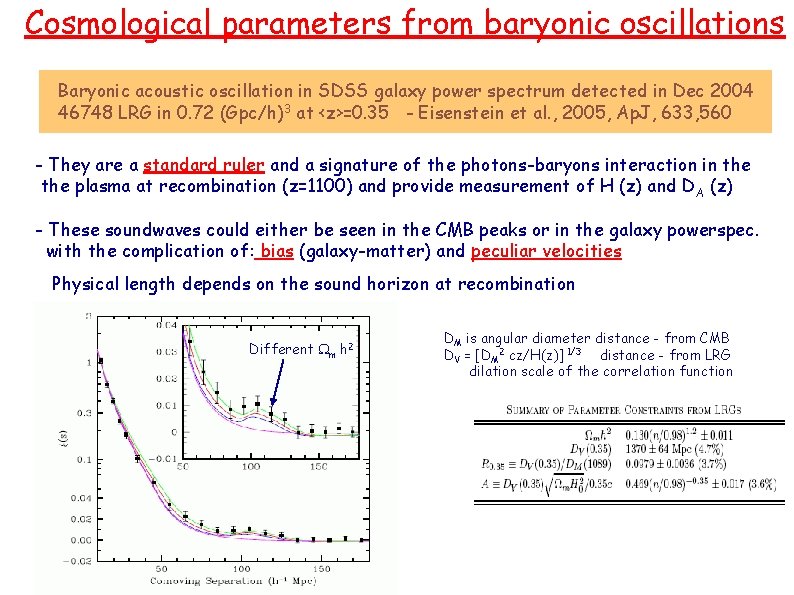
Cosmological parameters from baryonic oscillations Baryonic acoustic oscillation in SDSS galaxy power spectrum detected in Dec 2004 46748 LRG in 0. 72 (Gpc/h)3 at <z>=0. 35 - Eisenstein et al. , 2005, Ap. J, 633, 560 - They are a standard ruler and a signature of the photons-baryons interaction in the plasma at recombination (z=1100) and provide measurement of H (z) and D A (z) - These soundwaves could either be seen in the CMB peaks or in the galaxy powerspec. with the complication of: bias (galaxy-matter) and peculiar velocities Physical length depends on the sound horizon at recombination Different Wm h 2 DM is angular diameter distance - from CMB DV = [DM 2 cz/H(z)] 1/3 distance - from LRG dilation scale of the correlation function