Structure Data Model www assignmentpoint com What is

Structure Data Model www. assignmentpoint. com

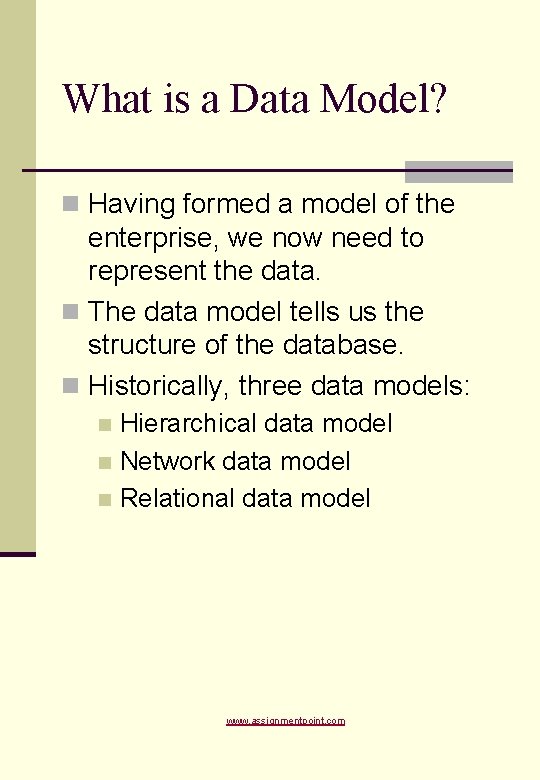
What is a Data Model? n Having formed a model of the enterprise, we now need to represent the data. n The data model tells us the structure of the database. n Historically, three data models: Hierarchical data model n Network data model n Relational data model n www. assignmentpoint. com

Hierarchical and Network Data Models n Hierarchical and network data models have been superseded by the relational data model. n Reasons: n Lack of expressive power n E. g. , one cannot express many-tomany relationships in the hierarchical model More closely tied to the underlying implementation. Hence, less data independence. n Relational data model has a clean mathematical basis. n www. assignmentpoint. com

The Relational Model n Due to Codd. n Everything is represented as a relation in the mathematical sense. Also called tables. n A database therefore is a collection of tables, each of which has a unique name, and each of which is described by a schema. n In addition, Codd defined a data manipulation language. www. assignmentpoint. com

Example of Schemas in the Relational Model n Example of a representation of entity sets: Student(sid, name, addr) Course(cid, title, eid) Empl(eid, ename, deptid) Dept(deptid, dname, loc) n Primary keys are underlined. n Recall that a primary key is one that uniquely identifies an entity. n An entity is a row in a table. www. assignmentpoint. com

More Example Schemas n Relationship sets between entity sets are also represented in tables. n Example of a table corresponding to a relationship: Enrol(sid, cid, grade) n Again, a relationship is represented by a row (or a tuple) in a relation. www. assignmentpoint. com

Relational Databases: Basic Concepts I n Attribute: n A column in a table n Domain n The set of values from which the values of an attribute are drawn. n Null value n A special value, meaning “not known” or “not applicable”. n Relation schema n A set of attribute names www. assignmentpoint. com

Relational Databases: Basic Concepts II n Tuple n A set of values, one for each attribute in the relation scheme over which the tuple is defined, i. e. a mapping from attributes to the appropriate domains n Relation instance n A set of tuples over the scheme of the relation www. assignmentpoint. com

Relational Databases: Basic Concepts III n Relational Database n A set of relations, each with a unique name n Normalized Relation n A relation in which every value is atomic (non-decomposable). Hence, every attribute in every tuple has a single value. www. assignmentpoint. com

Keys n Candidate Key n A minimal set of attributes that uniquely identifies a tuple n Primary Key n The candidate key chosen as the identifying key of the relation n Alternate Key n Candidate keys which are not primary keys www. assignmentpoint. com

n Foreign Key n An attribute (or set of attributes) in table R 1 which also occurs as the primary key of relation R 2 is called the referenced relation. n Foreign keys are also called connection keys or reference attributes. www. assignmentpoint. com

Integrity Rules: Entity Constraint n Entity constraint n All attributes in a primary key must be non-null. n Motivation: If the primary key uniquely identifies an entity in an entity set, then we must ensure that we have all the relevant information www. assignmentpoint. com

Integrity Rules: Referential Integrity n Referential integrity n A database cannot contain a tuple with a value for a foreign key that does not match a primary key value in the referenced relation. n Or, a foreign key must refer to a tuple that exists. n Motivation: If referential integrity were violated, we could have relationships between entities that we do not have any information about. www. assignmentpoint. com

Data Manipulation Languages n In order for a database to be useful, it should be possible to store and retrieve information from it. This is the role of the data manipulation language. n One of the attractions of the relational data model is that it comes with a well-defined data manipulation language. www. assignmentpoint. com

Types of DML n Two types of data manipulation languages n Navigational (procedural) n n The query specifies (to some extent) the strategy used to find the desired result e. g. relational algebra. Non-navigational(non-procedural) n The query only specifies what data is wanted, not how to find it e. g. relational calculus. www. assignmentpoint. com

Relational Algebra n Codd defined a number of algebraic operations for the relational model. n Unary operations take as input a single table and produce as output another table. n Binary operations take as input two tables and produce as output another table. www. assignmentpoint. com

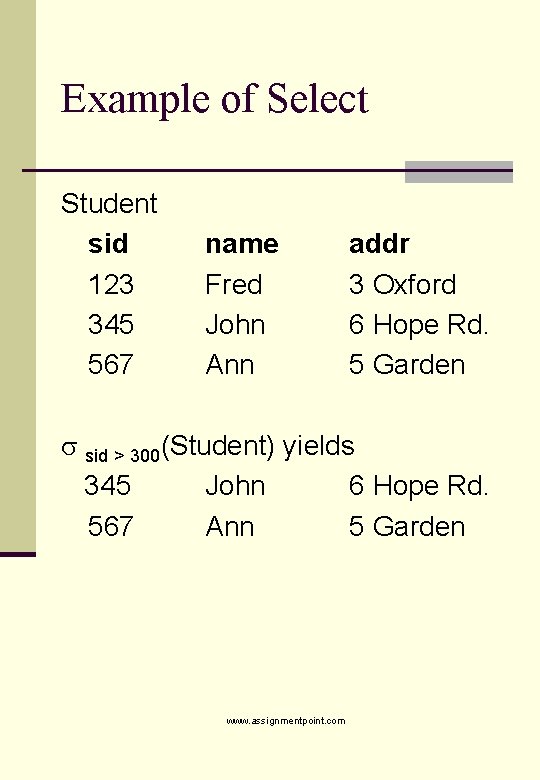
Unary Operations: Select n Select produces a table that only contains the tuples that satisfy a particular condition, in other words a “horizontal” subset. n Appearance: s. C(R) where C is a selection condition n and R is the relation over which the selection takes place n www. assignmentpoint. com

Example of Select Student sid 123 345 567 name Fred John Ann addr 3 Oxford 6 Hope Rd. 5 Garden sid > 300(Student) yields 345 John 6 Hope Rd. 567 Ann 5 Garden www. assignmentpoint. com

Unary Operations: Project n Project produces a table consisting of only some of the attributes. It creates a “vertical” subset. n Note that a project eliminates duplicates. n Appearance: ПA(R) where A is a set of attributes of R n and R is the relation over which the project takes place. n www. assignmentpoint. com

Example of Project Enrol sid 123 234 345 cid CS 51 T CS 52 S Пcid(Enrol) yields CS 51 T CS 52 S www. assignmentpoint. com grade 76 50 55

Binary Operations n Two relations are (union) compatible if they have the same set of attributes. n Example, one table may represent suppliers in one country, while another table with same schema represents suppliers in another country. n For the union, intersection and set-difference operations, the relations must be compatible. www. assignmentpoint. com

Union, Intersection, Setdifference n R 1 R 2 n The union is the table comprised of all tuples in R 1 or R 2. n R 1 R 2 n The intersection is the table comprised of all tuples in R 1 and R 2 n R 1 - R 2 n The set-difference between R 1 and R 2 is the table consisting of all tuples in R 1 but not in R 2. www. assignmentpoint. com

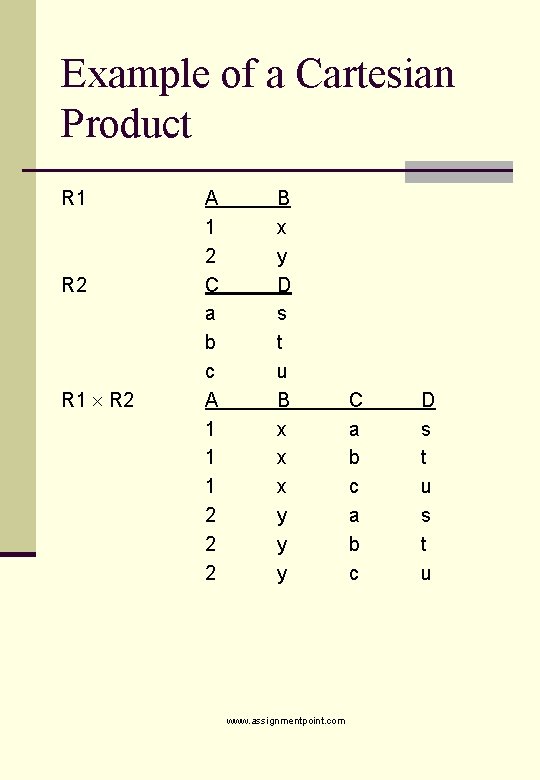
Cartesian Product n R 1 R 2 n The Cartesian product is the table consisting of all tuples formed by concatenating each tuple in R 1 with a tuple in R 2, for all tuples in R 2. www. assignmentpoint. com

Example of a Cartesian Product R 1 R 2 R 1 R 2 A 1 2 C a b c A 1 1 1 2 2 2 B x y D s t u B x x x y y y www. assignmentpoint. com C a b c D s t u

Natural Join n R 1 R 2 n Assume R 1 and R 2 have attributes A in common. Natural join is formed by concatenating all tuples from R 1 and R 2 with same values for A, and dropping the occurrences of A in R 2 n R 1 R 2 = ПA’( C(R 1 R 2)) n n where C is the condition that the values for R 1 and R 2 are the same for all attributes in A and A’ is all attributes in R 1 and R 2 apart from the occurrences of A in R 2. hence, natural join is syntactic sugar www. assignmentpoint. com

Example of a Natural Join I Course cid CS 51 T CS 52 S CS 52 T CS 51 S title DBMS OS Networking ES Instructor eid 123 345 456 ename Rao Allen Mansingh www. assignmentpoint. com eid 123 345 456

Example of a Natural Join II Course cid CS 51 T CS 52 S CS 52 T CS 51 S Instructor title DBMS OS Net. . . ES eid 123 345 456 www. assignmentpoint. com ename Rao Allen Mansingh

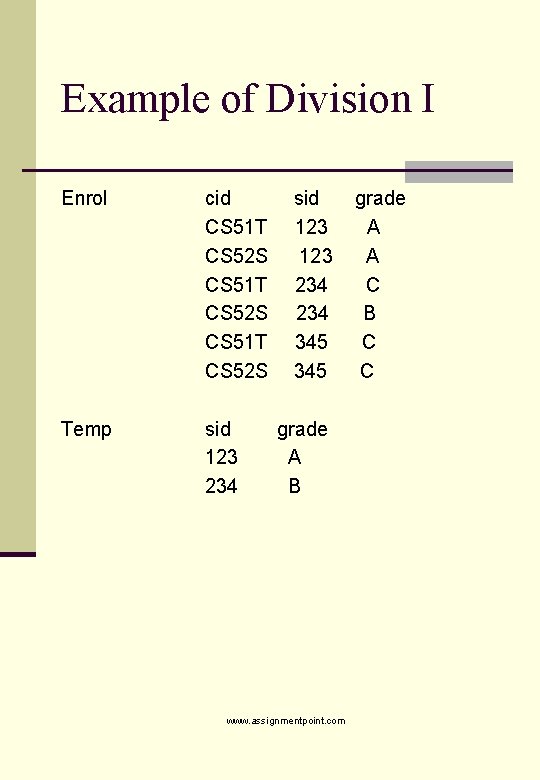
Division n R 1 R 2 n Assume that the schema for R 2 is a proper subset of the one for R 1. n We form the division by n n Ordering the tuples in R 1 so that all the tuples with the same value for the non-common attributes are grouped together. Each group contributes a tuple to the result if the group’s values on the common attributes form a superset of the values of these attributes in R 2. www. assignmentpoint. com

Example of Division I Enrol cid CS 51 T CS 52 S Temp sid 123 234 345 grade A B www. assignmentpoint. com grade A A C B C C

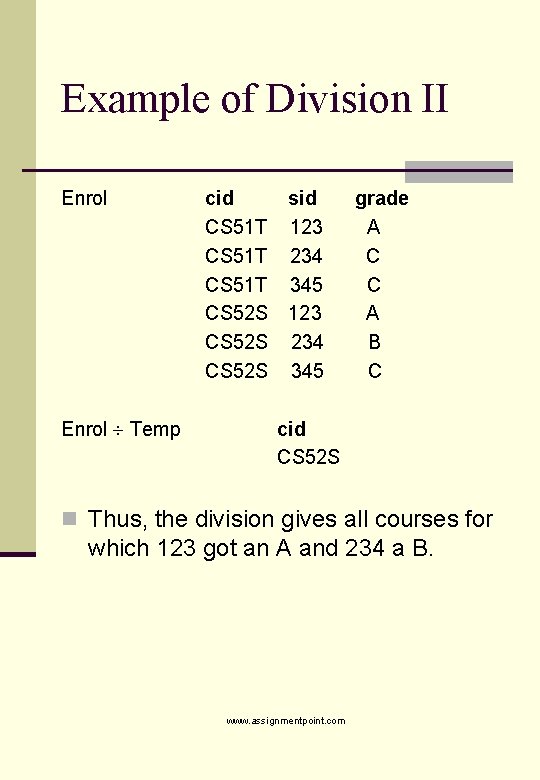
Example of Division II Enrol Temp cid sid CS 51 T 123 CS 51 T 234 CS 51 T 345 CS 52 S 123 CS 52 S 234 CS 52 S 345 grade A C C A B C cid CS 52 S n Thus, the division gives all courses for which 123 got an A and 234 a B. www. assignmentpoint. com

Assignment n Allows the expression to be written in parts. n Assigns the part to a temporary variable. n This variable can be used in subsequent expressions. n E. g. n sid( title = ‘DBMS’ (Enrol n Could be re-written as: n n Course) r Enrol Course sid( title = ‘DBMS’(r)) www. assignmentpoint. com

Rename Operation n Names the result of an expression. n x(A 1, A 2, …, An) (E) n returns the result of expression E under the name x with the attributes renamed as A 1, A 2, …, An. n E. g. S (Student) n Renames Student table to S. www. assignmentpoint. com

Database Modification n Insert n r E e. g. n Course n Delete n r n e. g. n Course {(‘CS 51 T’, ’DBMS’)} r - E Student - sid=‘ 1’(Student) n Update n r (r) F 1, F 2, …, Fn n e. g. n Enrol sid, cid, grade www. assignmentpoint. com grade + 2 (Enrol)

Examples n Assume the following schema: Student(sid, sname, saddr) Course(cid, title, lid) Enrol(sid, cid, grade) Lecturer(lid, lname, deptname) n Query 1: Find the name of all students that have taken the course entitled ‘Expert Systems’. n Query 2: Find the titles of all courses that student ‘Mark Smith’ has done. n Query 3: Find the id of students that have enrolled in all the courses that lecturer with id. = ‘ 234’ has taught. n Query 4: Find the highest grade for ‘CS 51 T’. www. assignmentpoint. com

Relational Calculus n A relational calculus expression defines a new relation in terms of other relations. n A tuple variable ranges over a named relation. So, its values are tuples from that relation. n Example: Get grades for CS 51 T n e(Enrol) {<e. grade>: e. cid = ‘CS 51 T’ } n www. assignmentpoint. com

Basic Syntax for Relational Calculus Expressions n r(R), …, s(S) { <target> : predicate} n where R, . . , S are tables n r, . . , s are tuple variables n target specifies the attributes of the resulting relation n predicate is a formula giving a condition that tuples must satisfy to qualify for the resulting relation. n www. assignmentpoint. com

The Predicate n Predicate is constructed from n attribute names n constants n comparison operators n logical connectives n quantified tuple variables t(R), t(R) www. assignmentpoint. com

Examples of Relational Calculus n Example 2 n Get names and grades for students enrolled in CS 51 T n e(Enrol), s(Student) {<s. name, e. grade>: e. cid = ‘CS 51 T’ s. sid = e. sid} n In relation algebra Пcid, name( CID =‘ CS 51 T’(Grade www. assignmentpoint. com Student))

Example 3 n Give the names of all students who got at least one A. n s(Student) {<s. name>: e(Enrol) (e. grade = ‘A’ s. sid = e. sid)} n Tuple variables not mentioned in the target list must be bound in the predicate. www. assignmentpoint. com

Example 4 n Get the names of all students who only got A’s n s(Student) {<s. name>: e(Enrol)( s. sid = e. sid e. grade = ‘A’) e 2(Enrol) (s. sid = e 2. sid)} www. assignmentpoint. com

Example 5 n Get the names of all students who got an A and a B n s(Student) {<s. name>: e(Enrol) (e. grade = ‘B’ s. sid = e. sid) e 2(Enrol) (e 2. grade = ‘A’ s. sid = e 2. sid)} www. assignmentpoint. com

Example 6 n Get the course titles and names for the courses for which the student did not get an A n c(Course), s(Student) {<s. name, c. title>: g(Enrol) s. sid = g. sid g. cid = c. cid g. grade ‘A’} www. assignmentpoint. com