Structure and Synthesis of Robot Motion Topics in

Structure and Synthesis of Robot Motion Topics in Control Subramanian Ramamoorthy School of Informatics 19 February, 2009

In this Lecture • We will survey some issues that occur in many realistic robotic systems and discuss control methods for dealing with them • We will look at three ideas: predictive, adaptive and nonlinear control • We will only try to get an understanding of what the essential issue is – detailed techniques beyond the scope of this lecture 19/02/2009 Structure and Synthesis of Robot Motion 2

Start from the Basics: A Simple System • Consider the mechanical system shown • From rest, if you apply force u(t), the position y(t) changes in response • In fact, the response is given by an ODE: • Define the state as: • You get equations of motion: 19/02/2009 Structure and Synthesis of Robot Motion k u(t) m b y(t) 3

How to Control the Simple System? • For any system of the general form (very often D = 0), • One could use many standard linear control techniques • For instance, linear quadratic regulator, u = - Kx • So, in general, properties of such a system are essentially that of the canonical system, 19/02/2009 Structure and Synthesis of Robot Motion 4

Properties of a Linear System 19/02/2009 Structure and Synthesis of Robot Motion 5

Properties of a Linear System, contd. Makes design convenient!t! 19/02/2009 Structure and Synthesis of Robot Motion 6

Is that It? Where are the Complications? In real robotics problems, we face many difficulties that are not captured in the simple model. Workspace may change (e. g. , Obstacles and constraints) at “run-time” - No longer possible to find and use global solutions System dynamics or operating conditions might change over time k u(t) m b 19/02/2009 y(t) Structure and Synthesis of Robot Motion Finally, most robot systems’ dynamics are more complex and non-linear 7

Ways to Deal with these Complications • Model Predictive Control Given a basic system dynamics model, pose long-term control problem as a sequence of finite-horizon optimal control problems – constraints can then be easily accommodated • Adaptive Control If system dynamics is going to change over time, estimate the changes continually and change controller accordingly • Nonlinear Control Finally, if the system dynamics is clearly nonlinear then one needs to do things differently – we will discuss linearization methods (many other possibilities exist!) 19/02/2009 Structure and Synthesis of Robot Motion 8

Model Predictive Control – Basic Idea Use a combination of system (sometimes called plant) model and state/control history to anticipate significant changes in control actions Example: Cruise control system in a car • Fuel sent to engine depends on desired cruise velocity and actual velocity of the car • Actual velocity depends on slope of the road (varies…) • An MPC would try to predict significant changes in slope and correct for it 19/02/2009 Structure and Synthesis of Robot Motion 9

Factors Influencing the MPC Problem 19/02/2009 Structure and Synthesis of Robot Motion 10

How does MPC differ from Simple Feedback? • What happens as the slope of the road increases? – Car velocity decreases – Fuel input to engine must be increased by the controller • In a traditional feedback controller (u = -Kx), car must first slow down for corresponding fuel increase – Controller catches up, but you have oscillations • A predictive controller uses knowledge of a finite-horizon forward in time to make corrections much earlier 19/02/2009 Structure and Synthesis of Robot Motion 11

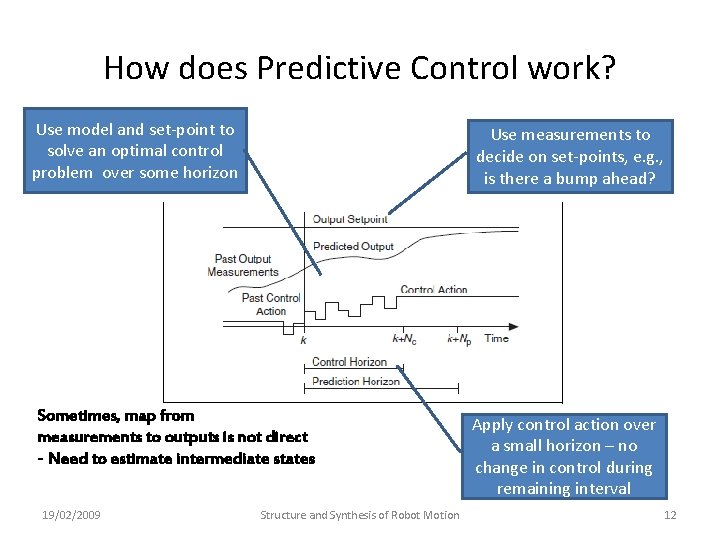
How does Predictive Control work? Use model and set-point to solve an optimal control problem over some horizon Use measurements to decide on set-points, e. g. , is there a bump ahead? Sometimes, map from measurements to outputs is not direct - Need to estimate intermediate states 19/02/2009 Structure and Synthesis of Robot Motion Apply control action over a small horizon – no change in control during remaining interval 12

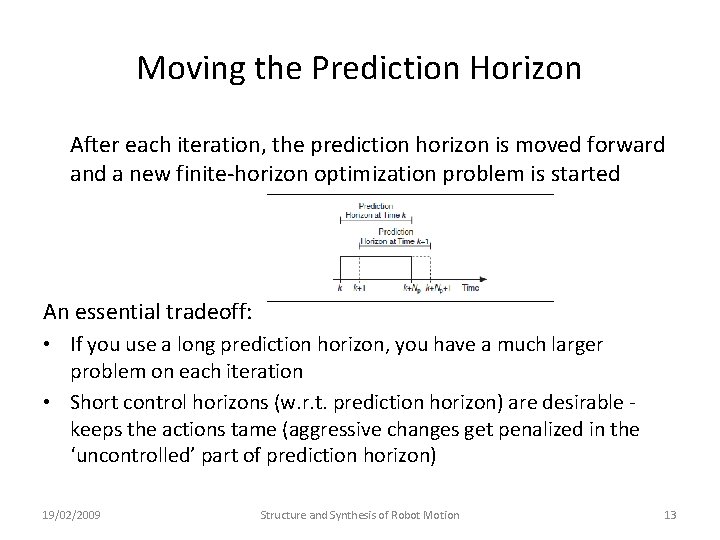
Moving the Prediction Horizon After each iteration, the prediction horizon is moved forward and a new finite-horizon optimization problem is started An essential tradeoff: • If you use a long prediction horizon, you have a much larger problem on each iteration • Short control horizons (w. r. t. prediction horizon) are desirable keeps the actions tame (aggressive changes get penalized in the ‘uncontrolled’ part of prediction horizon) 19/02/2009 Structure and Synthesis of Robot Motion 13

MPC – Problem Formulation [Source: ZK Nagy, ECMI 2004] 19/02/2009 Structure and Synthesis of Robot Motion 14

Important Feature of MPC - Constraints • Once the basic problem is setup as one of (numerical) optimal control, it becomes possible to incorporate constraints on the state and control equations – Inequality constraints, e. g. , actuator bounds – Equality constraints, e. g. , end-effector stays on a surface • The fact that the problem is repeatedly solved over a finite horizon means that these constraints can come and go 19/02/2009 Structure and Synthesis of Robot Motion 15

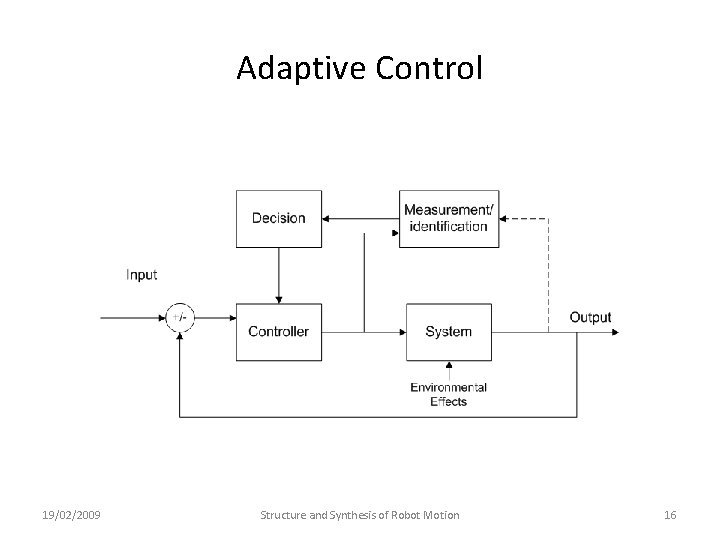
Adaptive Control 19/02/2009 Structure and Synthesis of Robot Motion 16

A Core Idea in Adaptive Control • Adaptive control is a well-established area with numerous possible architectures – we will not survey them all • Instead we will only look at one core idea: on-line determination of process parameters • If you can use a batch of data from a moving window to ‘identify’ the currently valid system model then we could adapt controller parameters accordingly • Ideally, all this happens on-line – one data point at a time! 19/02/2009 Structure and Synthesis of Robot Motion 17

Least Squares Estimation Known since Gauss (late 18 th century): 19/02/2009 Structure and Synthesis of Robot Motion 18

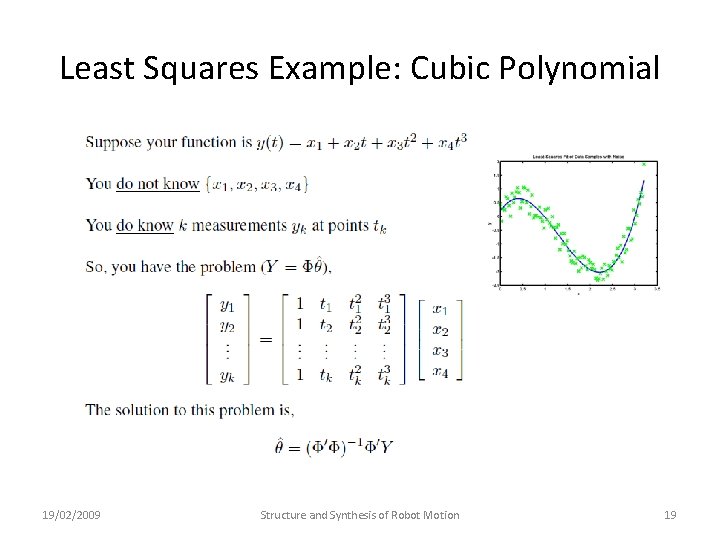
Least Squares Example: Cubic Polynomial 19/02/2009 Structure and Synthesis of Robot Motion 19

Least Squares can be Solved Recursively I am not going to show these equations and quantities like K(t) are derived. If you are curious, please refer to: - K. Astrom, B. Wittenmark, Adaptive Control, Addison-Wesley 1995 (Ch 2) - S. Satry, M. Bodson, Adaptive Control (on-line version), Ch 2 19/02/2009 Structure and Synthesis of Robot Motion 20

Nonlinear Control • Very few robotic systems actually exhibit linear dynamics across the entire state space – Variety of nonlinearity: limit stops, hysteresis, static friction, complex dynamics (e. g. , trigonometric terms in equations of motion) • There a number of different ways to cope with this: – One could deal with a specific nonlinearity in a “one-off” sense, e. g. , friction compensation – Many techniques (including MPC and Adaptive control) can cope with nonlinearities in a ‘slowly varying’ sense • Another alternative is to use systematic linearization tools from nonlinear control theory 19/02/2009 Structure and Synthesis of Robot Motion 21

Simple Idea: Jacobian Linearization 0 at equilibrium point Similar to a linear system, But, this is only true in that small neighbourhood! 19/02/2009 Structure and Synthesis of Robot Motion 22

Better Approach: Feedback Linearization • Algebraically transform nonlinear system dynamics into linear ones, so that linear control techniques can be applied • Different from using the Jacobian – feedback linearization is achieved by exact state transformation and feedback. • Used in many demanding applications ranging from mobile robotics and aircrafts to complex chemical processes • Biggest disadvantage is reliance on a good model – need significant sophistication to ensure robustness in practice 19/02/2009 Structure and Synthesis of Robot Motion 23

Feedback Linearization: Basic Procedure 19/02/2009 Structure and Synthesis of Robot Motion 24

Summary • This lecture surveyed three major techniques for controlling systems when they deviate from the assumptions of simple linear systems • We looked at – Model Predictive Control – Adaptive control – Nonlinear control • They all attack closely related issues but the focus of attention of each method is different 19/02/2009 Structure and Synthesis of Robot Motion 25