Structure and properties of colloidal glasses Peter Schall

Structure and properties of colloidal glasses Peter Schall Frans Spaepen Al Fernandez Nieves Johan Mattsson Dave Reichmann Dave Weitz Harvard Amsterdam Harvard Gothenburg Columbia Jaci Conrad Eric Weeks Hans Wyss Christoph Eisenman Param Dhillon NSF, NASA UIUC Emory Harvard Munich Columbia Relaxation in supercooled colloidal glasses: Correlated motion ‘Force’ chains Shear zones Flow of colloidal glasses Microgel glasses analogy to molecular glasses http: //www. seas. harvard. edu/projects/weitzlab UBC 7/21/07

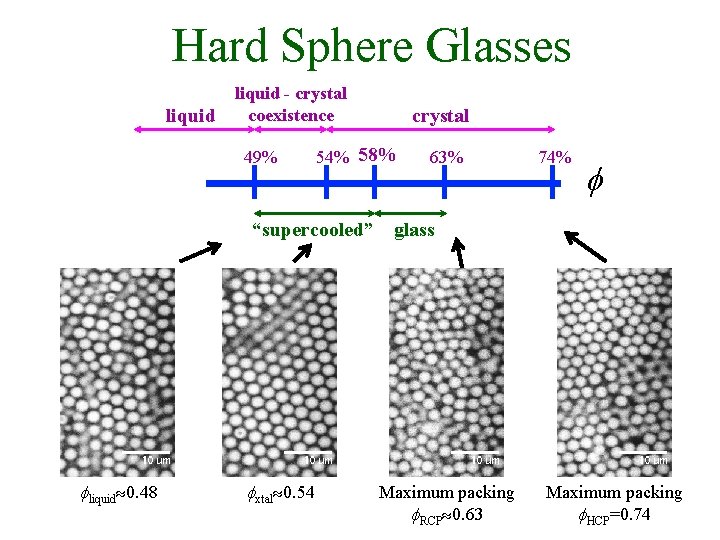
Hard Sphere Glasses liquid - crystal coexistence 49% crystal 54% 58% 63% 74% f “supercooled” glass fliquid 0. 48 fxtal 0. 54 Maximum packing f. RCP 0. 63 Maximum packing f. HCP=0. 74

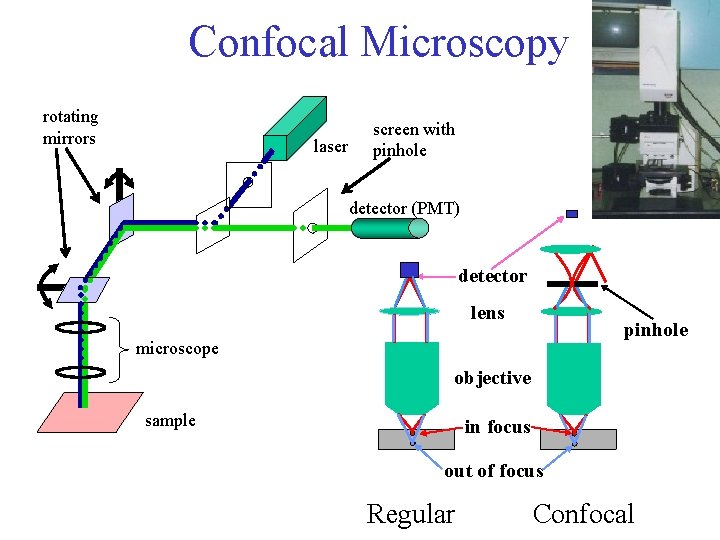
Confocal Microscopy rotating mirrors laser screen with pinhole detector (PMT) detector lens pinhole microscope objective sample in focus out of focus Regular Confocal

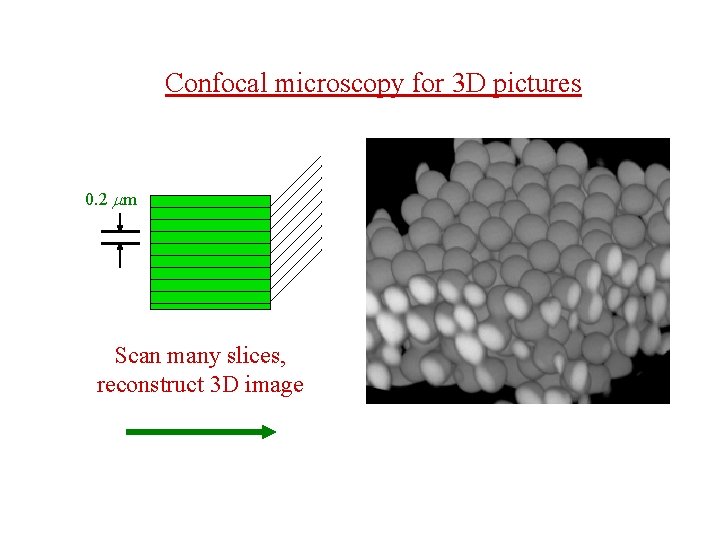
Confocal microscopy for 3 D pictures 0. 2 mm Scan many slices, reconstruct 3 D image

Brownian Motion (2 mm particles, dilute sample) y(t) 0. 5 mm time (s)

Diffusion: dilute samples Mean square displacement: x 2 (mm 2) Displacement distribution function: P( x) t=0. 5 s 10 -1 1 pe= Slo 10 -2 10 -3 10 -4 10 -5 t (s) Leads to 2 = 2 Dt x normal diffusion: Gaussian -2 0 x (mm) 2 Particle size a viscosity

Brownian Motion in Real Time

Voronoi polyhedra -Delaunay triangulation (“Wigner-Seitz cell”) defines nearest neighbor particles

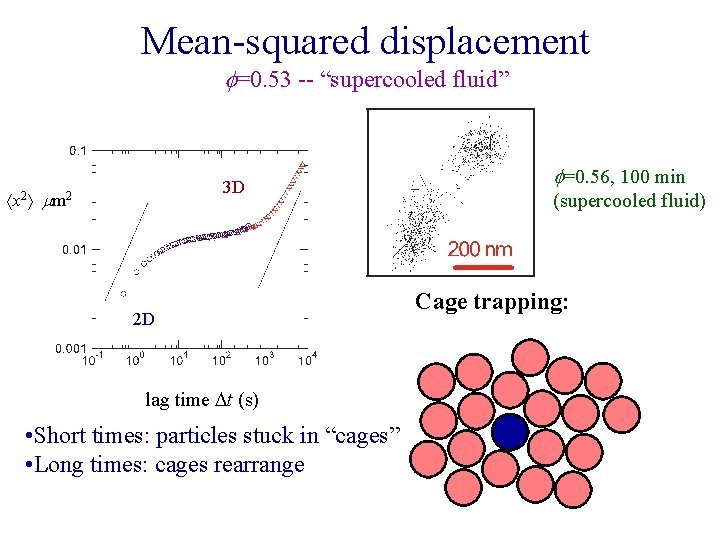
Mean-squared displacement f=0. 53 -- “supercooled fluid” 3 D x 2 mm 2 2 D lag time t (s) • Short times: particles stuck in “cages” • Long times: cages rearrange f=0. 56, 100 min (supercooled fluid) Cage trapping:

Trajectories of “fast” particles, f=0. 56 shading indicates depth 1 micron

Displacement distribution function 3 D x 2 mm 2 2 D lag time t (s) f = 0. 53: “supercooled fluid” Nongaussian Parameter t = 1000 s

Choose Time with Maximum Non-Gaussian Parameter

Structural Relaxations in a Supercooled Fluid time Number of relaxing particles Relaxing particles are highly correlated spatially

Structural Relaxations in a Glass time Number of relaxing particles Relaxing particles are NOT correlated spatially

Cluster size grows as glass transition is approached average cluster size volume fraction

What is a Glass? • Glass must have a low frequency shear modulus • Must have force chains to transmit stress

Identify Static Particles Topological Change: nn ( t) t 0+ t nn = 1 t 0+ t nn = 2 B. Doliwa and A. Heuer, J. Non-Cryst. Solids 307, 32 (2002).

Static Particles ( nn = 0) – f = 0. 56

Static Clusters Form Stress-Bearing Chains t f = 0. 52 f = 0. 56 f = 0. 60 Supercooled fluid Glass

Properties of Static Clusters Number of particles in cluster Mean square displacement Non-Gaussian parameter

Experiment and simulation agree Experiment Simulation

Elasticity is due to static clusters

Shear cell (micrometer screws) (piezo) bellow cover slip < 100 microns silicon wafer PMMA coating 5 mm

Shear profile z z y

Glasses : Collective relaxations

Glasses : Shear strain network Diffusion coefficient Shear energy

Effective diffusion coefficient depends on shear rate V ~ 4 particles

Glasses : Shear experiment metal grid

Glasses : Shear experiment metal grid 60 x 25 mm 3

Glasses : Particle tracking metal grid Particle Displacements, t = 30 min 60 x 25 mm 3 y average Dy strain rate 10 -5 s-1

Glasses : Particle tracking Average Shear Increase time resolution. . . 0 to 0. 2% + 0. 2 to 0. 4% + 0. 4 to 0. 6% + ? 0. 6 to 0. 8%

Glasses : Strain distribution Determine local shear strain • Find best Affine Deformation a, so that Ri ´ = Ri + a Ri Minimize mean-square difference D 2 = i (di – a Ri)2 Falk and Langer (1998) Strain tensor e : symmetric part of a Time t t+ t Ri R i´

Glasses : Strain distribution Cumulative strain Time t 0 Ri t 1 R i´ 1. 6 % shear z z x -y eyz -0. 1 - 0. 05 0. 1

Glasses : Strain distribution Cumulative strain Time t 0 Ri Ri´´ t 2 3. 0 % shear z z x -y eyz -0. 1 - 0. 05 0. 1

Glasses : Strain distribution Incremental strain eyz - z z y slope -3 eyz r / mm Continuum elasticity 1 eyz~ 3 r eyz - z x (Hutchinson, Spaepen, Schall) x / mm Identify volume of shear zone ~ 4 particles x

Glasses : Irreversible rearrangements Particle displacements 1. 6% z -x individual particle shear strain displacements shear strain > 0. 03 eyz 2 + y 2 + z 2)½ / a ( x - 0. 5 -0. 1 -1 - 0. 05 00 0. 5 0. 05 1 0. 1 -y

Glasses : Irreversible rearrangements Nearest neighbor change r 0 1. 3 r 0 4 3 2 1 Radial distribution t = 5 function min at 1. 6 % shear 0 t = 30 min t = 60 min # lost nearest neighbors

Glasses : Strain distribution 1. 6% Nucleation of shear event z -x 1. 2 ->1. 4 % 1. 4 ->1. 6 % -y yz xy Strain is initially in opposite direction -0. 6 -0. 4 -0. 2 0. 4 0. 6

Glasses : “Nucleation“ of shear events Modes of thermal fluctuations NO shear applied! eyz 0. 06 0. 04 0. 02 0 -0. 02 -0. 04 -0. 06 Strain distribution in subsequent 2. 5 min intervals.

Glasses : “Nucleation“ of shear events Modes of thermal fluctuations NO shear applied! Local strain eyz 0 z = 12. . 15 mm 0. 15 0. 1 x 0. 05 25 0 -0. 05 -0. 1 DV 50 Energy -0. 15 0 25 y 50 W = ½ m ( 2 eyz 2 ) V Shear Modulus m = 0. 056 Pa Boltzmann distribution f ~ exp{-m. V/k. BT}

Glasses : “Nucleation“ of shear events Nucleation energy: E = Ef – t Energy cost of Shear Event Formation ½ (2 meij 2 + lekk 2) d. V “Activation volume“ Energy gain due to applied stress t t 2 eyz d. V l: Lamé constant m: shear modulus n: Poisson ratio

Glasses : “Nucleation“ of shear events “Activation volume“ E = Ef – t Nucleation energy: Energy cost of Shear Event Formation Energy gain due to applied stress t 0. 2 Activation volume: = 4. 5 V 0 0. 1 Ef = 32. 9 14. 5 k. T t = 3. 0 2. 0 k. T 0 -0. 1 -0. 2 Ef – t = 29. 5 12. 5 k. T

Glasses : “Nucleation“ of shear events Nucleation energy: E = Ef – t “Activation volume“ Integration with e 0=0. 08 Ef = 18 k. T t = 1. 5 k. T E = 16. 5 k. T Nucleation rate: J = n f 0 exp(-E/k. T) (1/300) s-1 #particles 3500 attempt frequency 100 s-1 E = 18. 5 k. T

Glasses : Shear strain network z=16 mm z = 0. . . 20 mm Coupling through elastic field induces new shear zones

Colloids don’t behave like molecular glasses Strong Hard sphere colloids are always fragile Fragile

Increase stiffness of microgels Microgel D particles D~70 nm Interpenetrating network of PNIPAM & polyacrylic acid PNIPAM H - CH 2 - C - PAAc T H - C - n N COOH C Microgel O particles are deformable “Volume” fractions can be greater than 1 NH CH elasticity to determine deformability Control CH 3

Dynamic relaxation Stiffer Softer

Scaled dynamic structure factors Stiffer b ~ 0. 6 Softer b ~ 0. 8

Fragile and strong glasses

Comparison to molecular glasses Strong Fragile

Conclusions • Dynamic heterogeneities in supercooled fluids • ‘Force chains’ in supercooled fluids • Thermal nucleation of localized shear zones • Flow reflects elastically coupled shear zones • Microgel particles allow for more varied behavior