Structure and Motion JeanClaude Latombe Computer Science Department

Structure and Motion Jean-Claude Latombe Computer Science Department Stanford University NSF-ITR Meeting on November 14, 2002

Stanford’s Participants PI’s: L. Guibas, J. C. Latombe, M. Levitt Research Associate: P. Koehl Postdocs: F. Schwarzer, A. Zomorodian Graduate students: S. Apaydin (EE), S. Ieong (CS), R. Kolodny (CS), I. Lotan (CS), A. Nguyen (Sc. Comp. ), D. Russel (CS), R. Singh (CS), C. Varma (CS) § Undergraduate students: J. Greenberg (CS), E. Berger (CS) § Collaborating faculty: § § § § § A. Brunger (Molecular & Cellular Physiology) D. Brutlag (Biochemistry) D. Donoho (Statistics) J. Milgram (Math) V. Pande (Chemistry)

Problem Domains Biological functions derive from the structures (shapes) achieved by molecules through motions Determination, classification, and prediction of 3 D protein structures Modeling of molecular energy and simulation of folding and binding motion

What’s New/Interesting for Computer Science? Massive amount of experimental data Importance of similarities Multiple representations of structure Continuous energy functions Many objects forming deformable chains Many degrees of freedom Ensemble properties of pathways

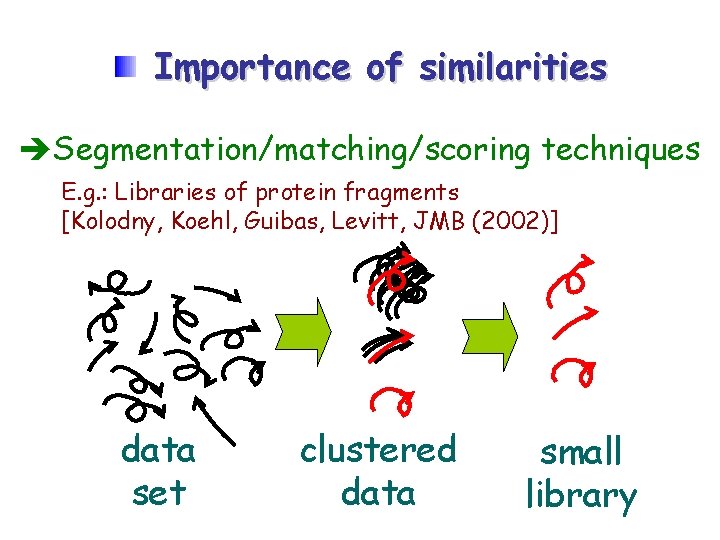
Importance of similarities Segmentation/matching/scoring techniques E. g. : Libraries of protein fragments [Kolodny, Koehl, Guibas, Levitt, JMB (2002)] data set clustered data small library

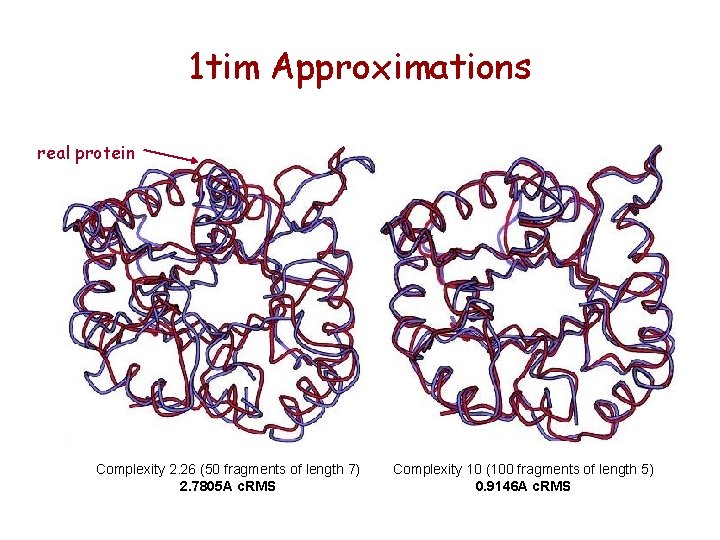
1 tim Approximations real protein Complexity 2. 26 (50 fragments of length 7) 2. 7805 A c. RMS Complexity 10 (100 fragments of length 5) 0. 9146 A c. RMS

Alignment of Structural Motifs [Singh and Saha; Kolodny and Linial] Problem: Determine if two structures share common motifs: • 2 (labelled) structures in R 3 • A={a 1, a 2, …, an}, B={b 1, b 2, …, bm} Find subsequences sa and sb s. t the substructures {as (1), as (2), …, as (l)} {bs (1), bs (2), …, bs (l)} are similar a b a a b b § Twofold problem: alignment and correspondence § Score Approximation Complexity

[R. Singh and M. Saha. Identifying Structural Motifs in Proteins. Pacific Symp. on Biocomputing, Jan. 2003. ] Iterative Closest Point (Besl-Mc. Kay) for alignment: Score: RMSD distance

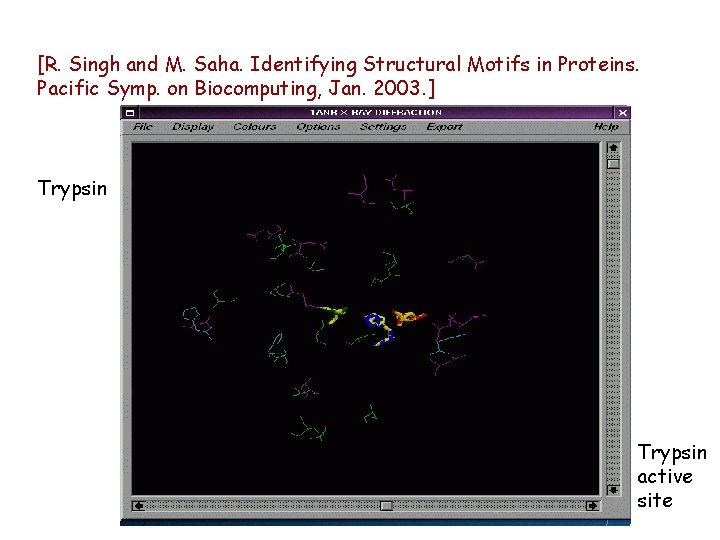
[R. Singh and M. Saha. Identifying Structural Motifs in Proteins. Pacific Symp. on Biocomputing, Jan. 2003. ] Trypsin active site

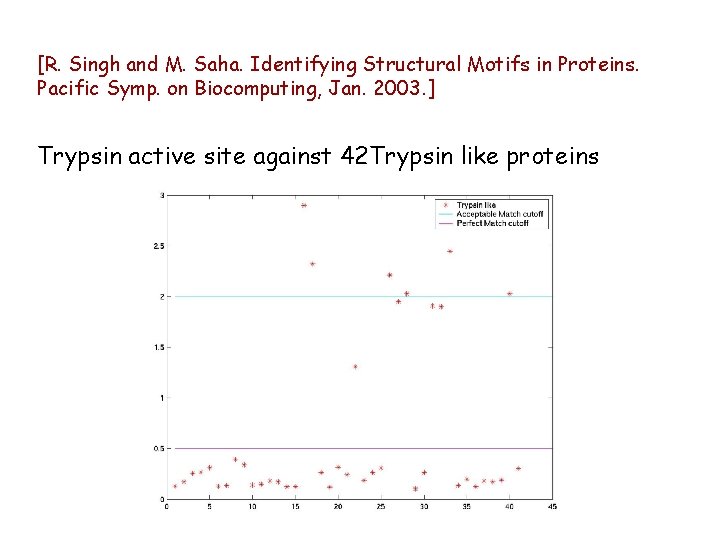
[R. Singh and M. Saha. Identifying Structural Motifs in Proteins. Pacific Symp. on Biocomputing, Jan. 2003. ] Trypsin active site against 42 Trypsin like proteins

Multiple representations of structure Pro. Shape software [Koehl, Levitt (Stanford), Edelsbrunner (Duke)]

Statistical potentials for proteins based on alpha complex [Guibas, Koehl, Zomorodian] § Decoys generated using “physical” potentials §Select best decoys using distance information

Continuous energy function Many objects in deformable chains Many pairs of objects, but relatively few are close enough to interact During motion simulation - detect steric clashes (self-collisions) - find pairs of atoms closer than cutoff - find which energy terms can be reused Data structures that capture proximity, but undergo small or rare changes

Other application domains: § Modular reconfigurable robots § Reconstructive surgery

§ Fixed Bounding-Volume hierarchies don’t work § Instead, exploit what doesn’t change: chain topology Adaptive BV hierarchies [Guibas, Nguyen, Russel, Zhang] [Lotan, Schwarzer, Halperin, Latombe] (SOCG’ 02) sec 17

Wrapped bounding sphere hierarchies [Guibas, Nguyen, Russel, Zhang] (So. CG 2002) • WBSH undergoes small number of changes • Self-collision: O(n logn ) in R 2 O(n 2 -2/d) in Rd, d 3

Chain. Trees [Lotan, Schwarzer, Halperin, Latombe] (So. CG’ 02)

Chain. Trees [Lotan, Schwarzer, Halperin, Latombe] (So. CG’ 02) Assumption: Few degrees of freedom change at each motion step (e. g. , Monte Carlo simulation) Updating: Finding interacting pairs: (in practice, sublinear)

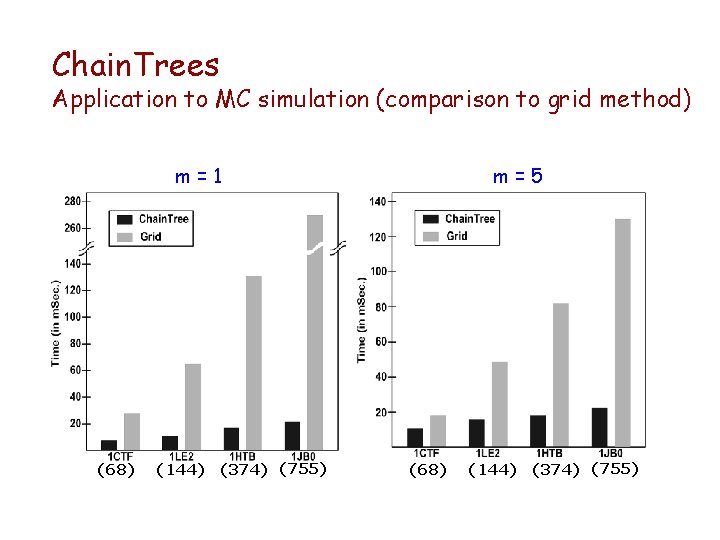
Chain. Trees Application to MC simulation (comparison to grid method) m=1 (68) (144) (374) (755) m=5 (68) (144) (374) (755)

Many degrees of freedom Tools to explore large dimensional conformational (structure) spaces: - Structure sampling [Kolodny, Levitt] - Finding nearest neighbors [Lotan, Schwarzer]

Sampling structures by combining fragments [Kolodny, Levitt] Library of protein fragments a b c d Discrete set of candidate structures bbc cab

Nearest neighbors in high-dimensional space [Lotan, Schwarzer] Find k nearest neighbors of a given protein conformation in a set of n conformations (c. RMS, d. RMS) Idea: Cut backbone into m equal subsequences a 0 a 3 a 1 a 2 a 4 a 5 a 6 am

Nearest neighbors in high-dimensional space [Lotan and Schwarzer] 100, 000 decoys of 1 CTF (Park-Levitt set) Computation of 100 NN of each conformation Full rep. , d. RMS (brute force) Ave. rep. , d. RMS (brute force) : SVD red. rep. , d. RMS (brute force) SVD red. rep. , d. RMS (kd-tree) ~84 h ~4. 8 h 41 min 19 min ~80% of computed NNs are true NNs kd-tree software from ANN library (U. Maryland)

Ensemble properties of pathways Stochastic nature of molecular motion requires characterizing average properties of many pathways Probabilistic conformational roadmaps Applications to protein folding and ligand-protein binding [Apaydin, Brutlag, Guestrin, Hsu, Latombe]

Example: Probability of Folding pfold HIV integrase [Du et al. ‘ 98] 1 - pfold “We stress that we do not suggest using pfold as a transition coordinate for practical purposes as it is Folded set Unfolded set very computationally intensive. ” Du, Pande, Grosberg, Tanaka, and Shakhnovich “On the Transition Coordinate for Protein Folding” Journal of Chemical Physics (1998).

Probabilistic Roadmap [Apaydin, Brutlag, Hsu, Guestrin, Latombe] (RECOMB’ 02, ECCB’ 02) Idea: Capture the stochastic nature of molecular motion by a network of randomly selected conformations and by assigning probabilities to edges vi Pij vj

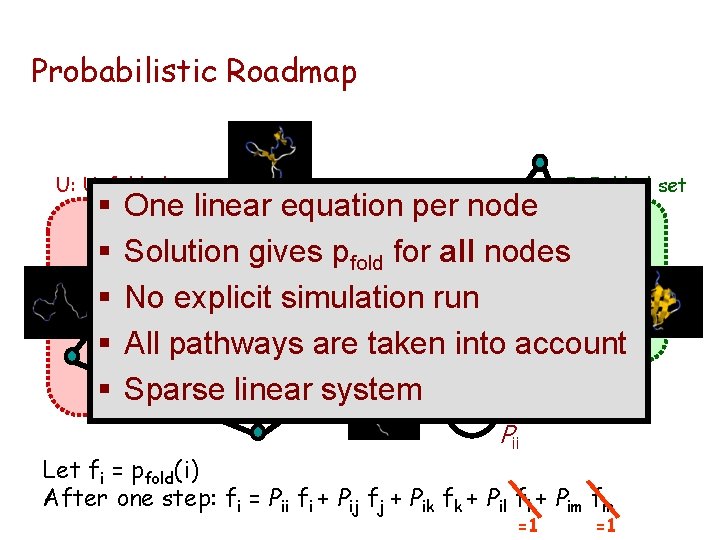
Probabilistic Roadmap U: Unfolded set § § § F: Folded set One linear equation per node Solution gives pfold for all nodes l k No explicit simulation run j Pik Pil All pathways are taken Pij into account m Pim Sparse linear system i Pii Let fi = pfold(i) After one step: fi = Pii fi + Pij fj + Pik fk + Pil fl + Pim fm =1 =1

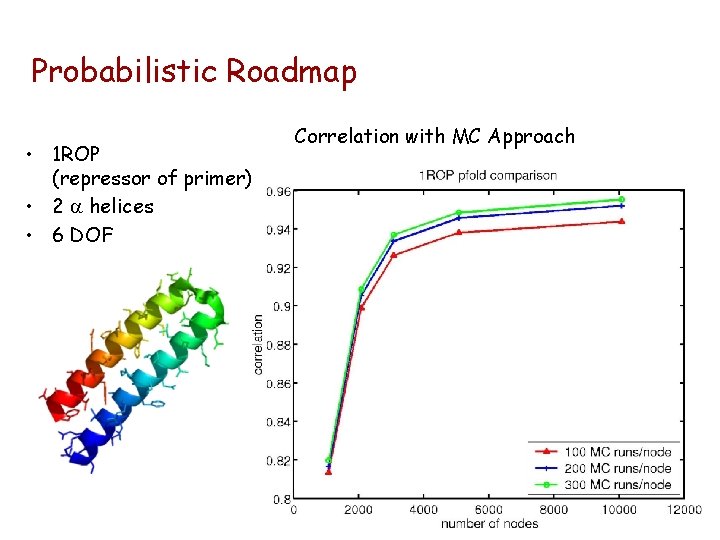
Probabilistic Roadmap • 1 ROP (repressor of primer) • 2 a helices • 6 DOF Correlation with MC Approach

Probabilistic Roadmap Computation Times (1 ROP) Monte Carlo: 49 conformations Over 11 days of computer time Over 106 energy computations 1 - 1. 5 hours of computer time ~15, 000 energy computations Roadmap: 5000 conformations ~4 orders of magnitude speedup!

Summary • Interpretation of electron density maps • Biology • Statistical potential • Modeling • Library of protein fragments • Self-collision and energy maintenance • Structure alignment • Pro. Shape software • Tools for high-dimensional spaces • Probabilistic roadmaps – Structure determination – Shape representation – Hierarchies • Algorithms – Deformation – Motion planning – Shape organization • Software – Alpha shapes

Future Work Perform more substantial experiments E. g. , more realistic potentials in Chain. Tree and probabilistic roadmaps Extend tools to solve more relevant problems E. g. , encode Molecular Dynamics into probabilistic roadmaps Combine results E. g. , use library of fragments to sample probabilistic roadmaps Develop new algorithms/data structures E. g. , sparse spanners to capture proximity information

Our Future: The Bio. X – Clark Center June 2003