STRUCTURE A structure is a rigid body made

STRUCTURE • A structure is a rigid body made up of several connected parts or members designed to withstand some externally applied forces. • The analysis of structures is based on the principle that if a structure is in equilibrium, then each of its members is also in equilibrium. • By applying the equations of equilibrium to the various parts of simple truss, frame or machine, the forces acting on the connections can be determined.

STRUCTURE An engineering structure is any connected system of members built to support or transfer forces and to safely withstand the load applied to it. Structure are said to be statically determinate when the forces & reaction produced by a given loading can be calculated by using only equation of equilibrium.
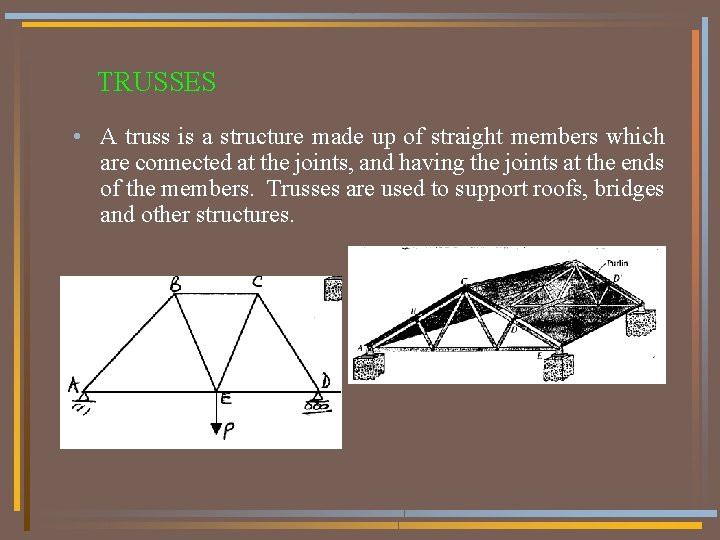
TRUSSES • A truss is a structure made up of straight members which are connected at the joints, and having the joints at the ends of the members. Trusses are used to support roofs, bridges and other structures.

APPLICATIONS Trusses are commonly used to support a roof. For a given truss geometry and load, how can we determine the forces in the truss members and select their sizes? A more challenging question is that for a given load, how can we design the trusses’ geometry to minimize cost?

APPLICATIONS (continued) Trusses are also used in a variety of structures like cranes and the frames of aircraft or space stations. How can we design a light weight structure that will meet load, safety, and cost specifications?



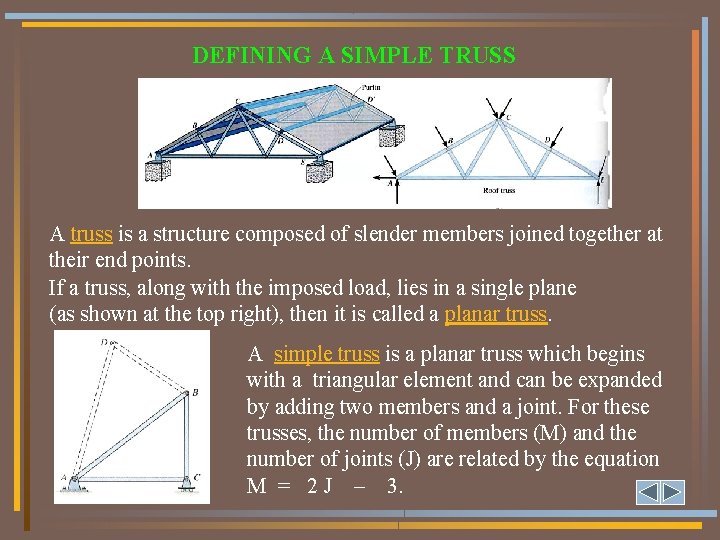
DEFINING A SIMPLE TRUSS A truss is a structure composed of slender members joined together at their end points. If a truss, along with the imposed load, lies in a single plane (as shown at the top right), then it is called a planar truss. A simple truss is a planar truss which begins with a triangular element and can be expanded by adding two members and a joint. For these trusses, the number of members (M) and the number of joints (J) are related by the equation M = 2 J – 3.

ANALYSIS and DESIGN ASSUMPTIONS When designing both the member and the joints of a truss, first it is necessary to determine the forces in each truss member. This is called the force analysis of a truss. When doing this, two assumptions are made: 1. All loads are applied at the joints. The weight of the truss members is often neglected as the weight is usually small as compared to the forces supported by the members. 2. The members are joined together by smooth pins. This assumption is satisfied in most practical cases where the joints are formed by bolting or welding. With these two assumptions, the members act as two-force members. They are loaded in either tension or compression. Often compressive members are made thicker to prevent buckling.
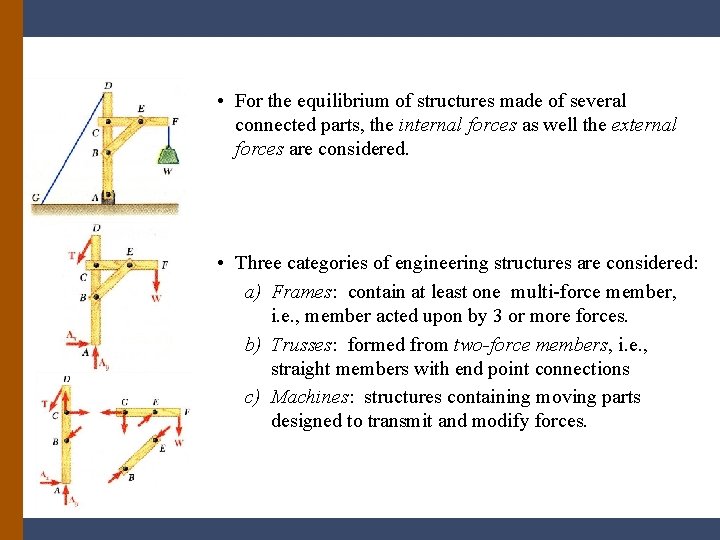
• For the equilibrium of structures made of several connected parts, the internal forces as well the external forces are considered. • Three categories of engineering structures are considered: a) Frames: contain at least one multi-force member, i. e. , member acted upon by 3 or more forces. b) Trusses: formed from two-force members, i. e. , straight members with end point connections c) Machines: structures containing moving parts designed to transmit and modify forces.
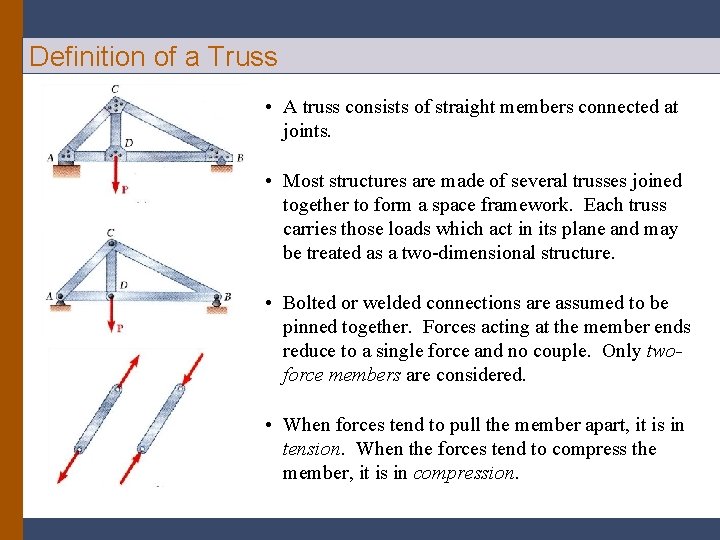
Definition of a Truss • A truss consists of straight members connected at joints. • Most structures are made of several trusses joined together to form a space framework. Each truss carries those loads which act in its plane and may be treated as a two-dimensional structure. • Bolted or welded connections are assumed to be pinned together. Forces acting at the member ends reduce to a single force and no couple. Only twoforce members are considered. • When forces tend to pull the member apart, it is in tension. When the forces tend to compress the member, it is in compression.
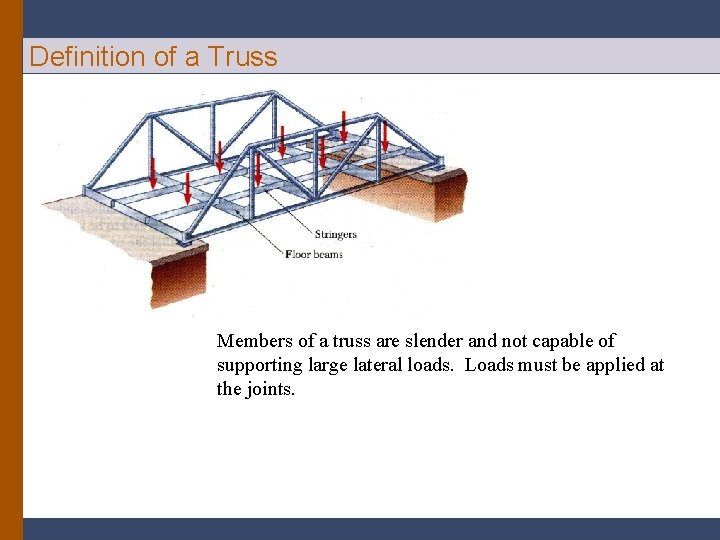
Definition of a Truss Members of a truss are slender and not capable of supporting large lateral loads. Loads must be applied at the joints.

Definition of a Truss

Examples of Trusses
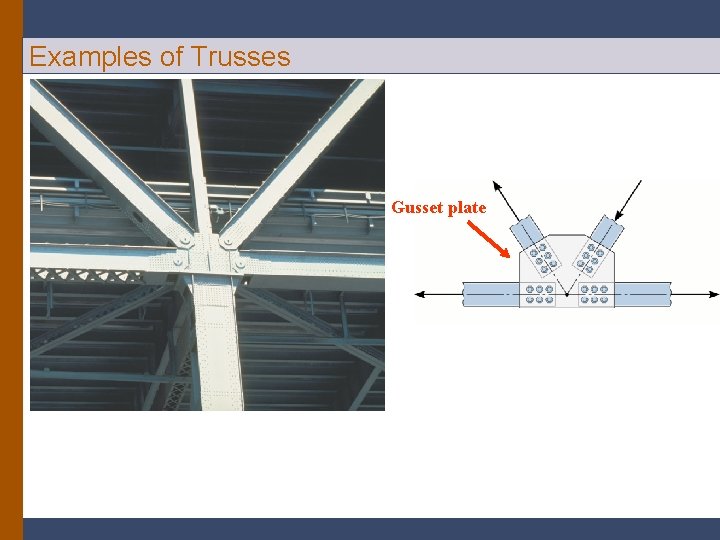
Examples of Trusses Gusset plate

Examples of Trusses The roof truss shown is formed by two planar trusses connected by a series of purlins.

Examples of Trusses - Because roof trusses, such as those shown, require support only at their ends, it is possible to construct buildings with large unobstructed floor areas.
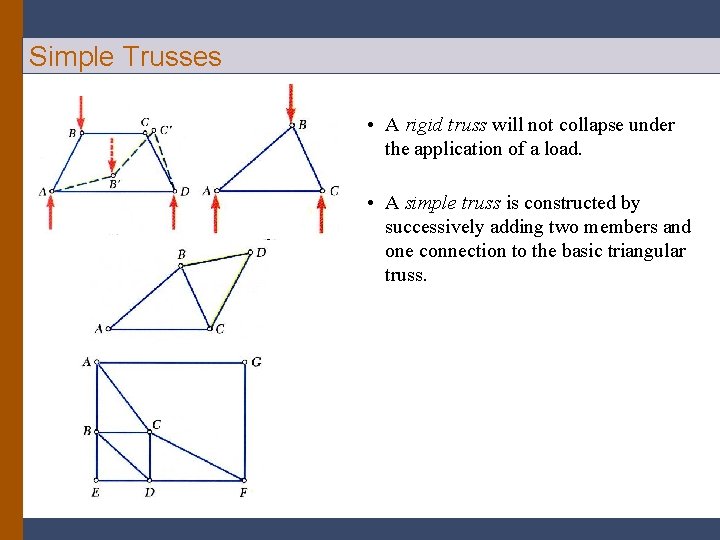
Simple Trusses • A rigid truss will not collapse under the application of a load. • A simple truss is constructed by successively adding two members and one connection to the basic triangular truss.

Space Trusses Three-dimensional or space trusses are used for broadcast and power transmission line towers, roof framing, and spacecraft applications, such as components of the International Space Station.

THE METHOD OF JOINTS In this method of solving for the forces in truss members, the equilibrium of a joint (pin) is considered. All forces acting at the joint are shown in a FBD. This includes all external forces (including support reactions) as well as the forces acting in the members. Equations of equilibrium ( FX= 0 and FY = 0) are used to solve for the unknown forces acting at the joints.

STEPS FOR ANALYSIS 1. If the support reactions are not given, draw a FBD of the entire truss and determine all the support reactions using the equations of equilibrium. 2. Draw the free-body diagram of a joint with one or two unknowns. Assume that all unknown member forces act in tension (pulling the pin) unless you can determine by inspection that the forces are compression loads. 3. Apply the scalar equations of equilibrium, FX = 0 and FY = 0, to determine the unknown(s). If the answer is positive, then the assumed direction (tension) is correct, otherwise it is in the opposite direction (compression). 4. Repeat steps 2 and 3 at each joint in succession until all the required forces are determined.

ZERO-FORCE MEMBERS If a joint has only two non-colinear members and there is no external load or support reaction at that joint, then those two members are zero-force members. In this example members DE, CD, AF, and AB are zero force members. You can easily prove these results by applying the equations of equilibrium to joints D and A. Zero-force members can be removed (as shown in the figure) when analyzing the truss.

ZERO – FORCE MEMBERS (continued) If three members form a truss joint for which two of the members are collinear and there is no external load or reaction at that joint, then the third non-collinear member is a zero force member. Again, this can easily be proven. One can also remove the zero-force member, as shown, on the left, for analyzing the truss further. These members are used to increase the stability of the truss during construction and to provide support if the applied loading is changed.
- Slides: 24