STRUCTURAL MECHANICS Point loads The figure below illustrates

STRUCTURAL MECHANICS

Point loads § The figure below illustrates a simply supported beam with reactions at each end and two point loadings of 50 k. N and 100 k. N. § We shall calculate the value of the end reactions. Before undertaking this calculation, we need to recap some of the basic laws associated with this type of structure;

Point Loads § The sum of the forces in one direction must equal the sum of the forces in the opposite direction ie the sum of downward forces equals the sum of the upward forces. § Anti-clockwise moments equal clockwise moments

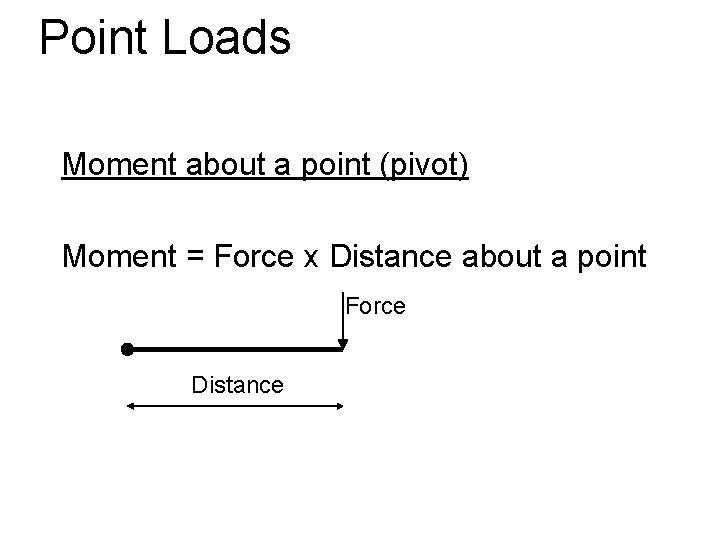
Point Loads Moment about a point (pivot) Moment = Force x Distance about a point Force Distance

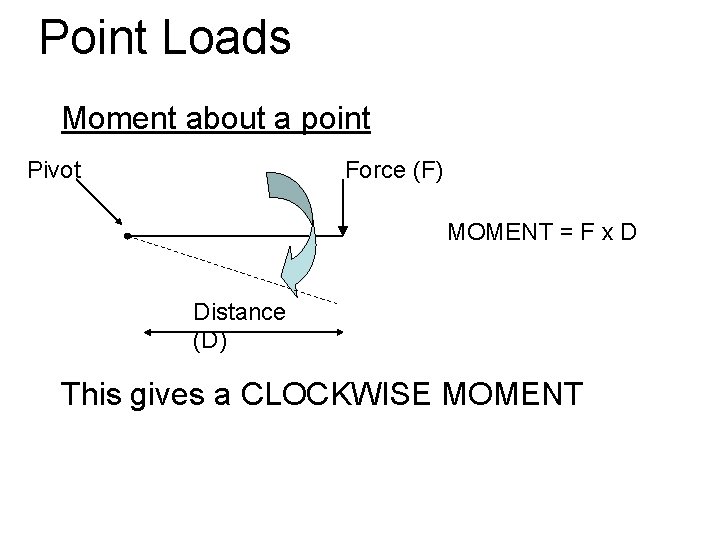
Point Loads Moment about a point Pivot Force (F) MOMENT = F x D Distance (D) This gives a CLOCKWISE MOMENT

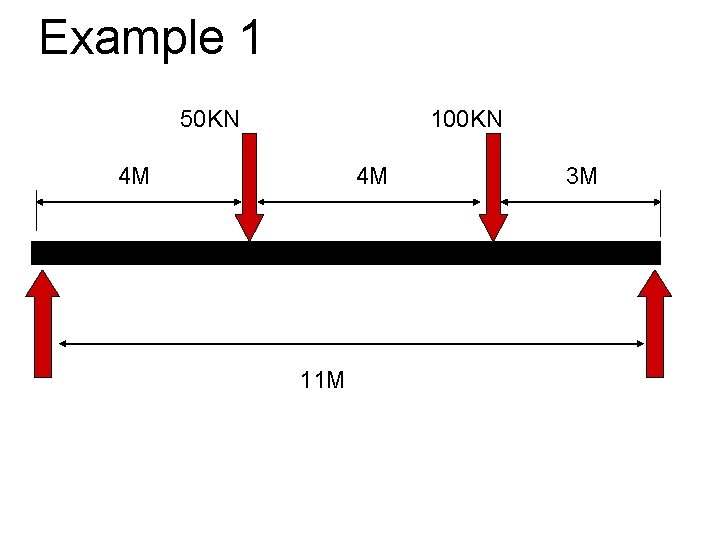
Example 1 50 KN 100 KN 4 M 4 M 11 M 3 M

Example 1 § Calculate the left and right reactions § Take the left-hand reaction as the PIVOT: § Anti-clockwise moments = Clockwise moments

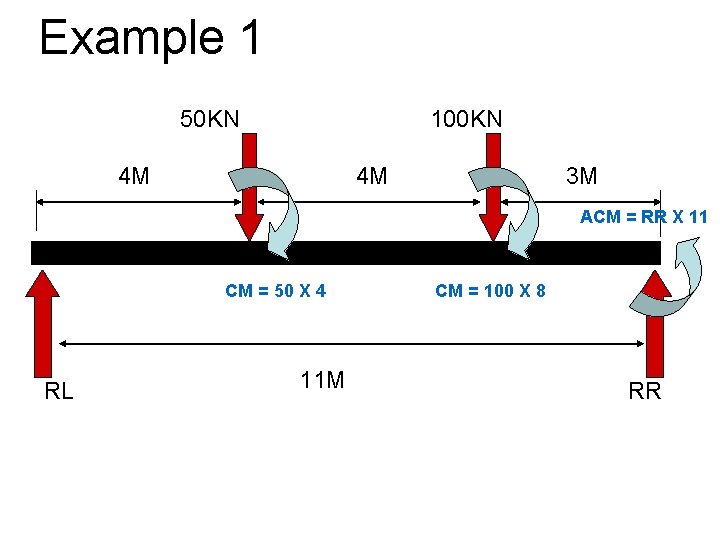
Example 1 50 KN 100 KN 4 M 4 M 3 M ACM = RR X 11 CM = 50 X 4 RL 11 M CM = 100 X 8 RR

Example 1 § Anti-clockwise moments = Clockwise moments § RR x 11 = (100 x 8) + (50 x 4) § RR x 11 = 1000 § RR = 1000/11 = 90. 91 Kn

Example 1 § Similarly, if we start at the right hand reaction: § Anti-clockwise moments= clockwise moments § (100 x 3) + (50 x 7) = RL x 11 § 650/11 = RL = 59. 09 Kn

Example 1 § RR = 90. 91 Kn § RL = 59. 09 k. N § Check ΣUPWARD FORCES = ΣDOWNWARD FORCES § 59. 09 + 90. 91 = 150 (50+100) correct

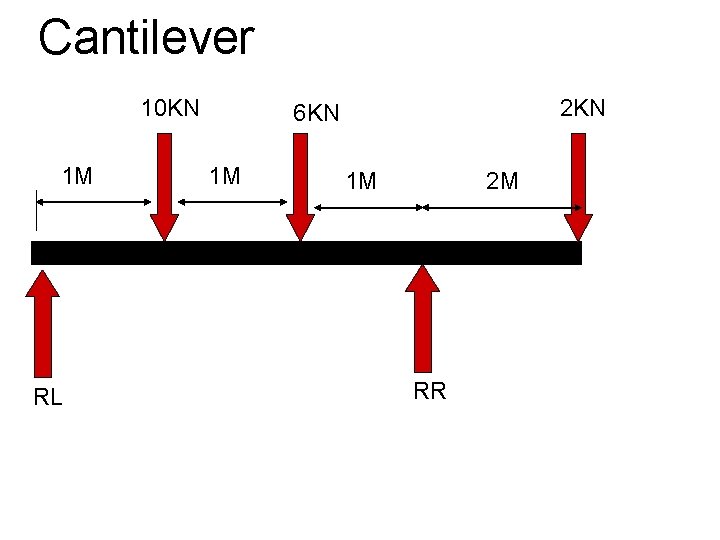
Cantilever 10 KN 1 M RL 2 KN 6 KN 1 M 1 M 2 M RR

Cantilever RR x 3 = (10 x 1) + (6 X 2) + (2 x 5) RR x 3 = 10 + 12 + 10 RR x 3 = 32 RR = 32/3 RR = 10. 67 k. N

Cantilever RR = 10. 67 k. N Total Downward Force = 18 k. N Therefore, RR + RL = 18 – RR RL = 18 – 10. 67 RL = 7. 33 k. N

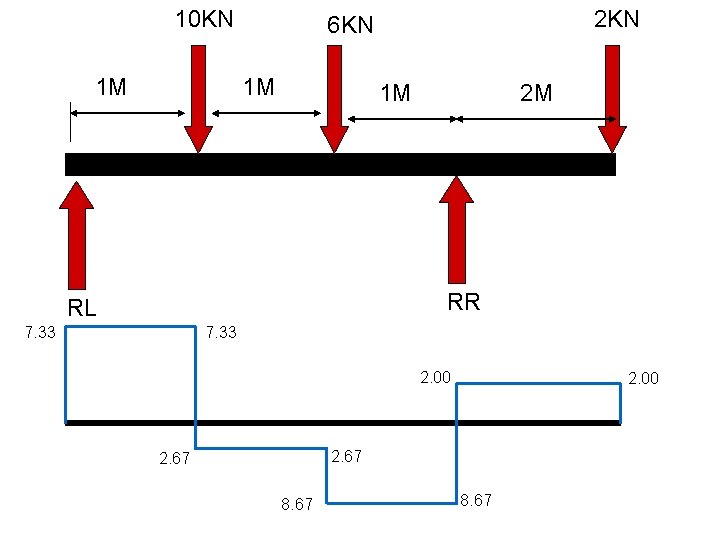
10 KN 1 M 2 KN 6 KN 1 M 1 M 2 M RR RL 7. 33 2. 00 2. 67 8. 67

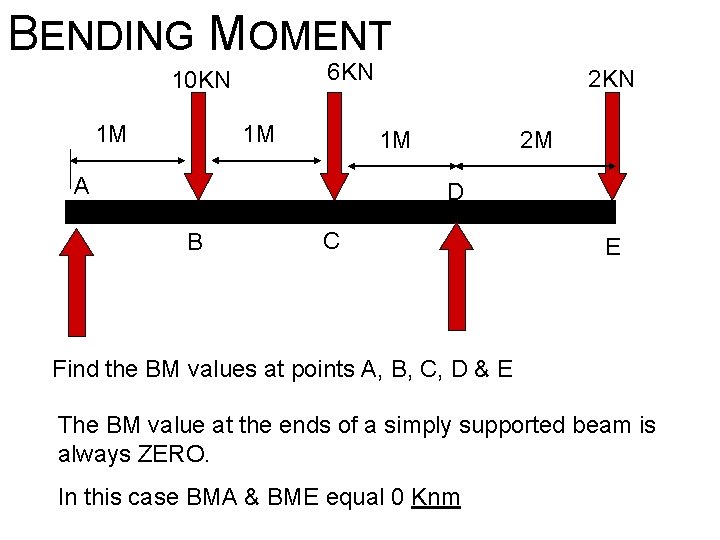
BENDING MOMENT 6 KN 10 KN 1 M 1 M 2 KN 1 M A 2 M D B C E Find the BM values at points A, B, C, D & E The BM value at the ends of a simply supported beam is always ZERO. In this case BMA & BME equal 0 Knm

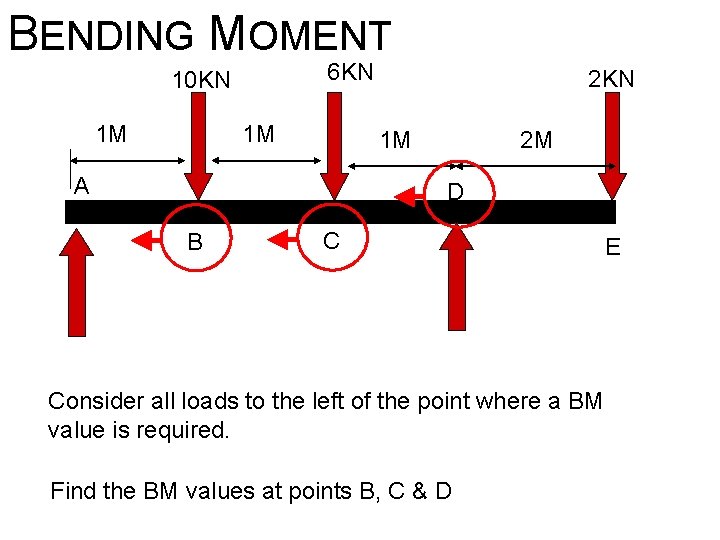
BENDING MOMENT 6 KN 10 KN 1 M 1 M 2 KN 1 M A 2 M D B C Consider all loads to the left of the point where a BM value is required. Find the BM values at points B, C & D E

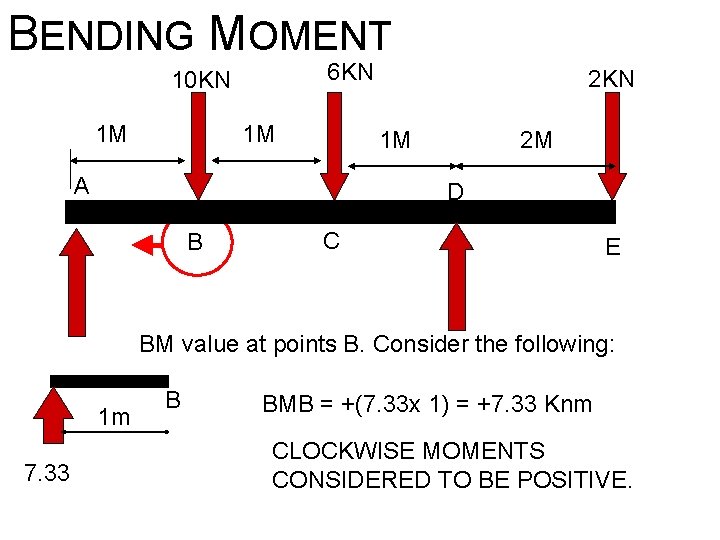
BENDING MOMENT 6 KN 10 KN 1 M 1 M 2 KN 1 M A 2 M D B C E BM value at points B. Consider the following: 1 m 7. 33 B BMB = +(7. 33 x 1) = +7. 33 Knm CLOCKWISE MOMENTS CONSIDERED TO BE POSITIVE.

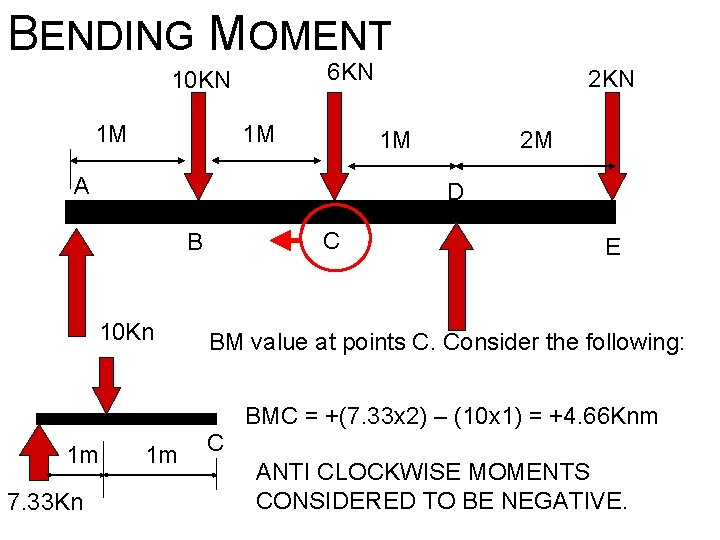
BENDING MOMENT 6 KN 10 KN 1 M 1 M 2 KN 1 M A 2 M D C B 10 Kn E BM value at points C. Consider the following: BMC = +(7. 33 x 2) – (10 x 1) = +4. 66 Knm 1 m 7. 33 Kn 1 m C ANTI CLOCKWISE MOMENTS CONSIDERED TO BE NEGATIVE.

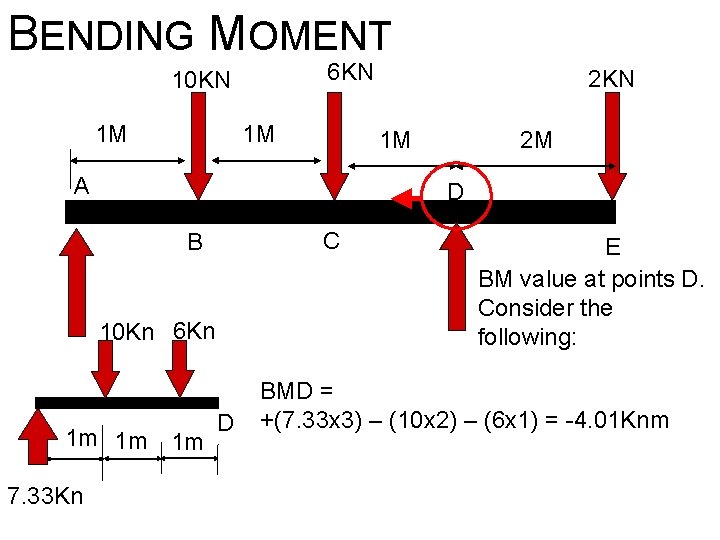
BENDING MOMENT 6 KN 10 KN 1 M 1 M 1 M A 2 M D C B 10 Kn 6 Kn 1 m 1 m 1 m 7. 33 Kn 2 KN D E BM value at points D. Consider the following: BMD = +(7. 33 x 3) – (10 x 2) – (6 x 1) = -4. 01 Knm

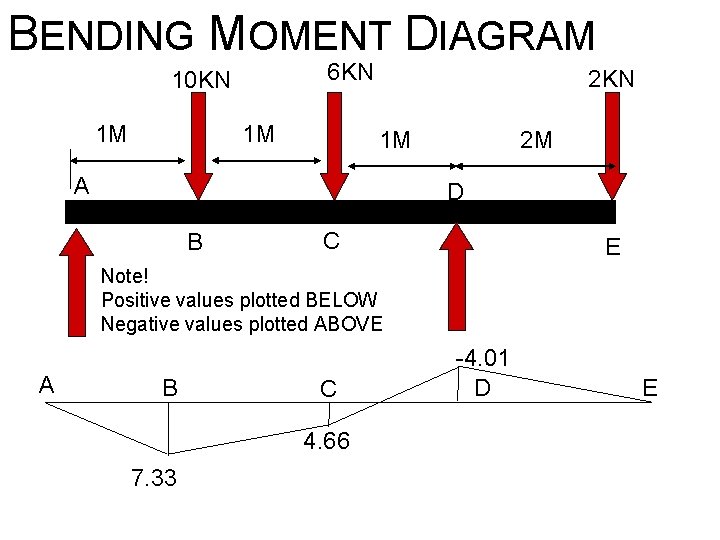
BENDING MOMENT DIAGRAM 6 KN 10 KN 1 M 1 M 2 KN 1 M A 2 M D B C E Note! Positive values plotted BELOW Negative values plotted ABOVE A B C 4. 66 7. 33 -4. 01 D E

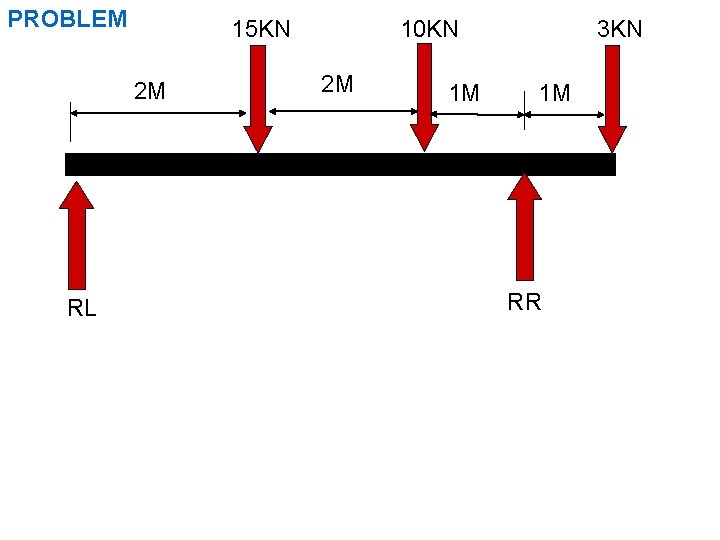
PROBLEM 15 KN 2 M RL 10 KN 2 M 1 M 3 KN 1 M RR

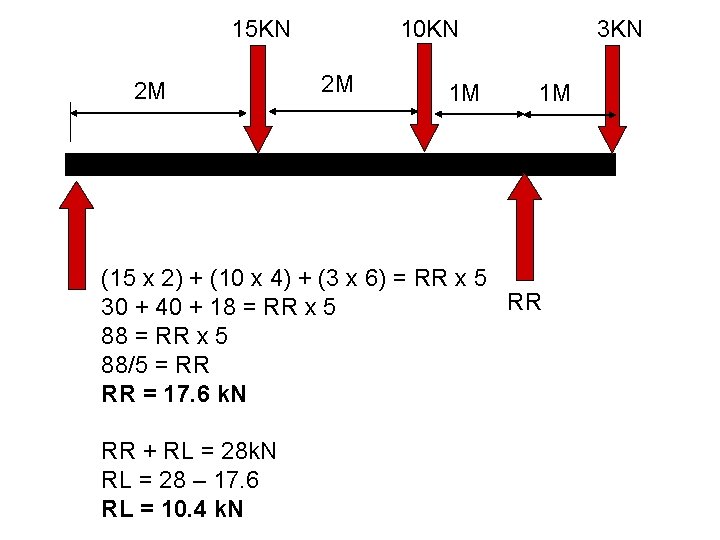
15 KN 2 M 10 KN 2 M 1 M 3 KN 1 M (15 x 2) + (10 x 4) + (3 x 6) = RR x 5 RR 30 + 40 + 18 = RR x 5 88/5 = RR RR = 17. 6 k. N RR + RL = 28 k. N RL = 28 – 17. 6 RL = 10. 4 k. N

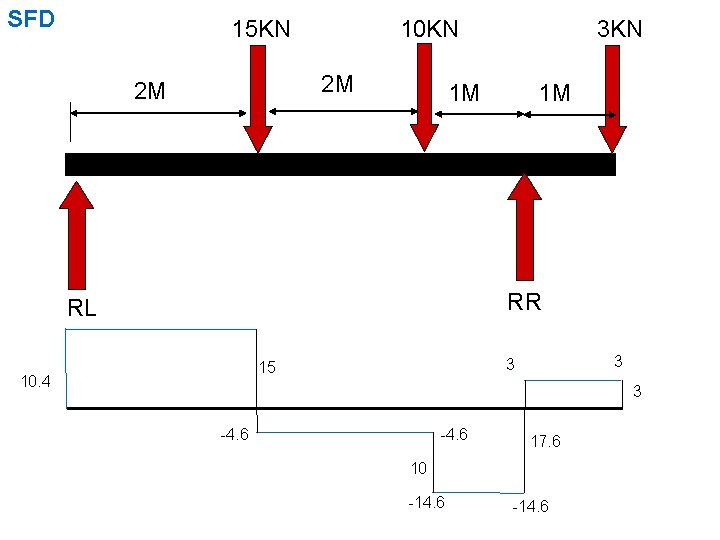
SFD 15 KN 10 KN 2 M 2 M 3 KN 1 M 1 M RR RL 10. 4 3 3 15 3 -4. 6 17. 6 10 -14. 6

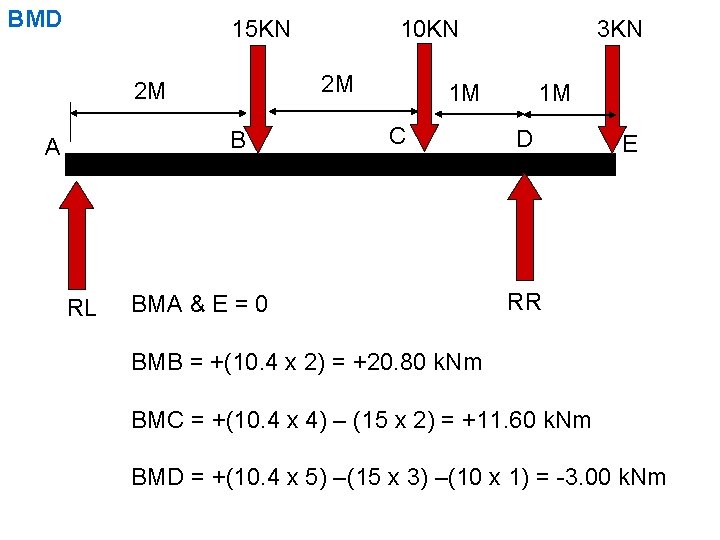
BMD 15 KN 2 M 2 M B A RL 10 KN 3 KN 1 M C BMA & E = 0 1 M D E RR BMB = +(10. 4 x 2) = +20. 80 k. Nm BMC = +(10. 4 x 4) – (15 x 2) = +11. 60 k. Nm BMD = +(10. 4 x 5) –(15 x 3) –(10 x 1) = -3. 00 k. Nm

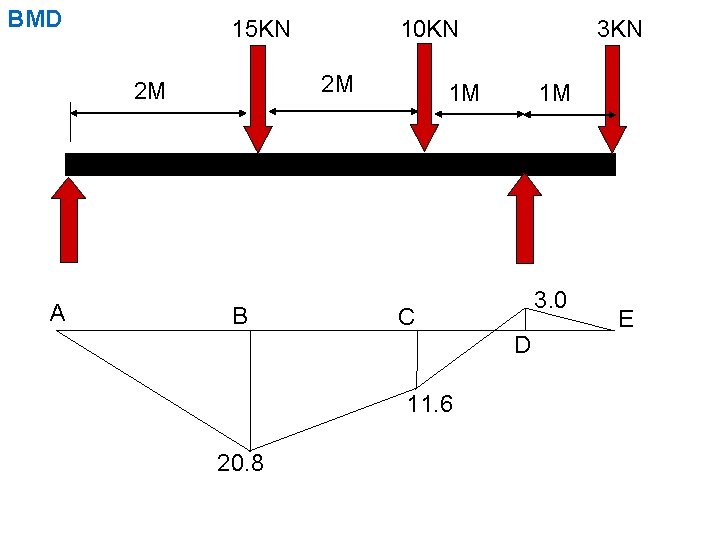
BMD 15 KN 2 M 2 M A 10 KN B 3 KN 1 M 1 M 3. 0 C D 11. 6 20. 8 E