Structural Join Algorithms Examples n n n Key

Structural Join Algorithms – Examples n n n Key property: x is a descendant (resp. , child) of y iff x. doc. Id = y. doc. Id & x. Start. Pos < y. Start. Pos <= y. End. Pos < x. End. Pos (and y. Level = x. Level+1). A node n for us is (D, S: E, L). Call this node id for convenience. What is structural join? given lists Alist and Dlist of nodes u output pairs (x, y) of nodes [x in Alist, y in Dlist], s. t. x is a <relative> of y. u frequently, assume i/p lists are ordered by node id. u might want to order o/p by first operand(‘s node id) or second. (what diff. does it make? ) u n TPQ = compute several SJs and stitch ‘em together. 1

SJ variants n There is also a so-called holistic join algorithm (Bruno, Koudas, and Srivastava SIGMOD 2002). u n Extend binary join ideas to finding matches for paths/twigs. In XML query processing, also need following variants of SJ: Given Alist and Dlist, whenever x in Alist has a relative y in Dlist, output (x, y); else just output x. (structural outerjoin). u Given …, output x in Alist whenever there exists y in Dlist such that y is a relative of x. (structural semijoin. ) u Given …, output x in Alist whenever it has no relative y in Dlist. (structural semi-antijoin. ) u 2

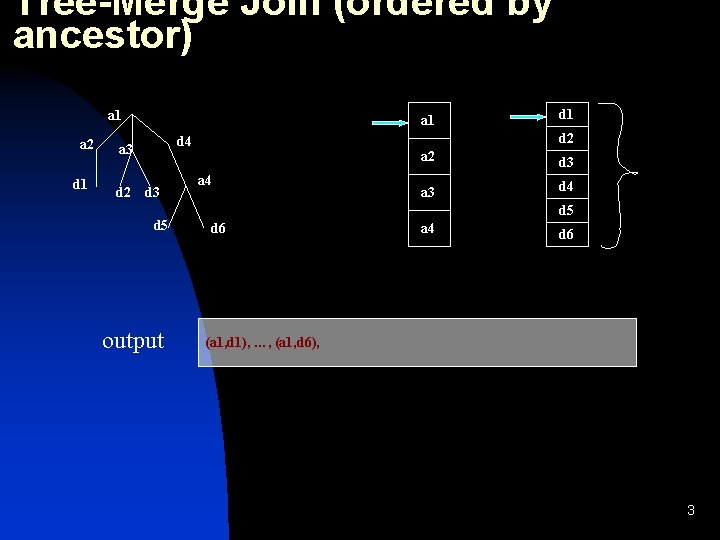
Tree-Merge Join (ordered by ancestor) a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), …, (a 1, d 6), 3

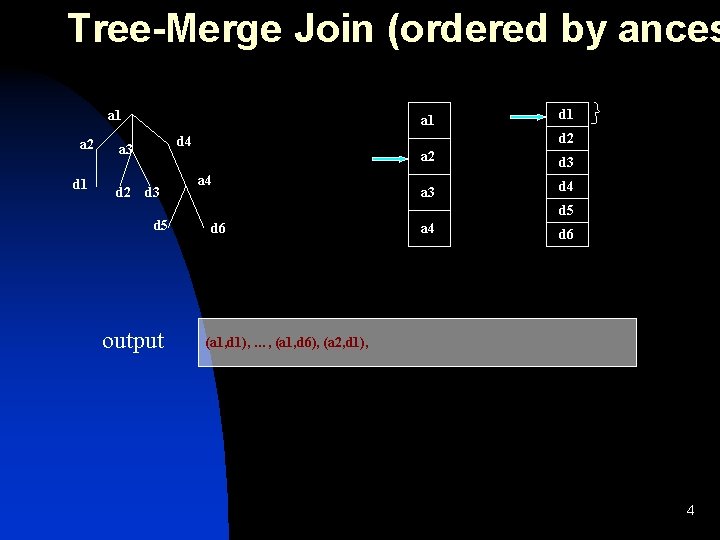
Tree-Merge Join (ordered by ances a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), …, (a 1, d 6), (a 2, d 1), 4

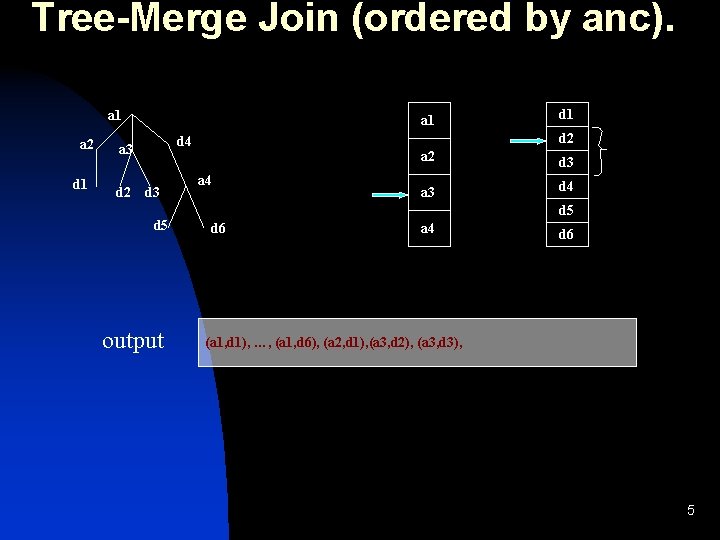
Tree-Merge Join (ordered by anc). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), …, (a 1, d 6), (a 2, d 1), (a 3, d 2), (a 3, d 3), 5

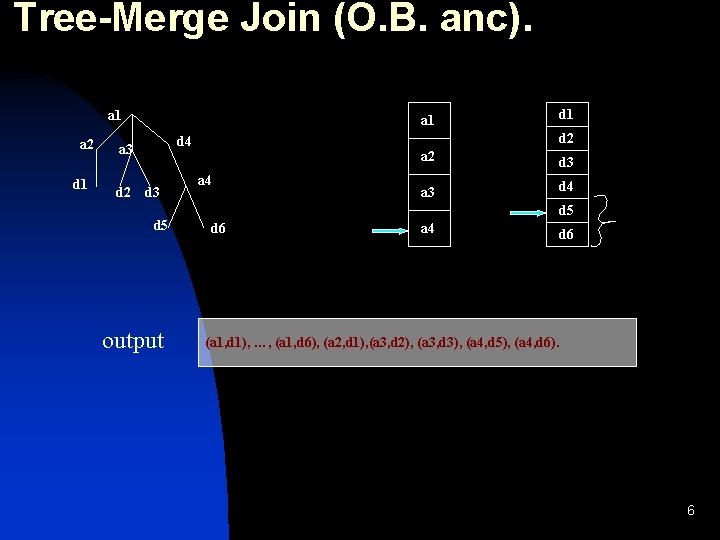
Tree-Merge Join (O. B. anc). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), …, (a 1, d 6), (a 2, d 1), (a 3, d 2), (a 3, d 3), (a 4, d 5), (a 4, d 6). 6

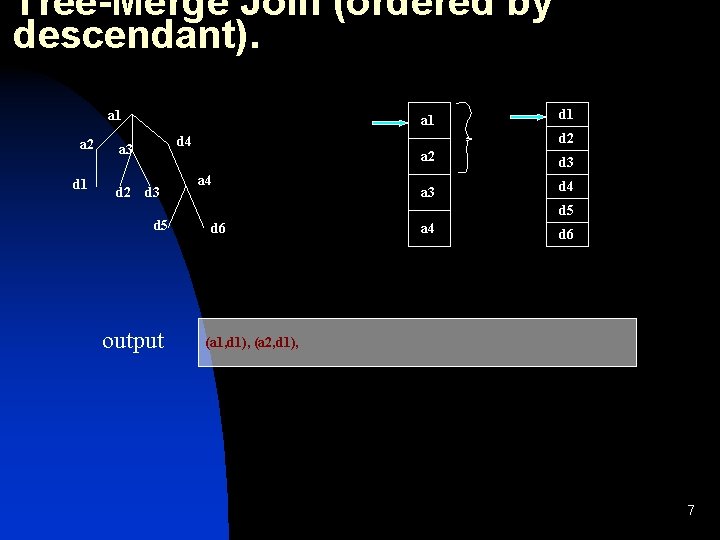
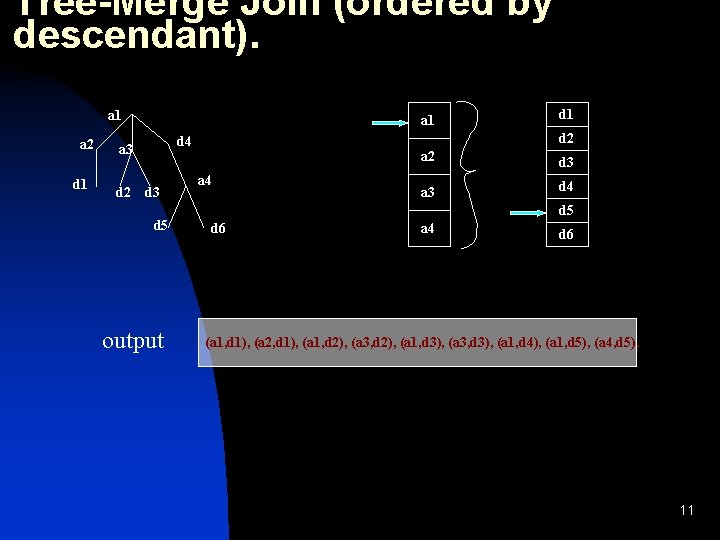
Tree-Merge Join (ordered by descendant). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), (a 2, d 1), 7

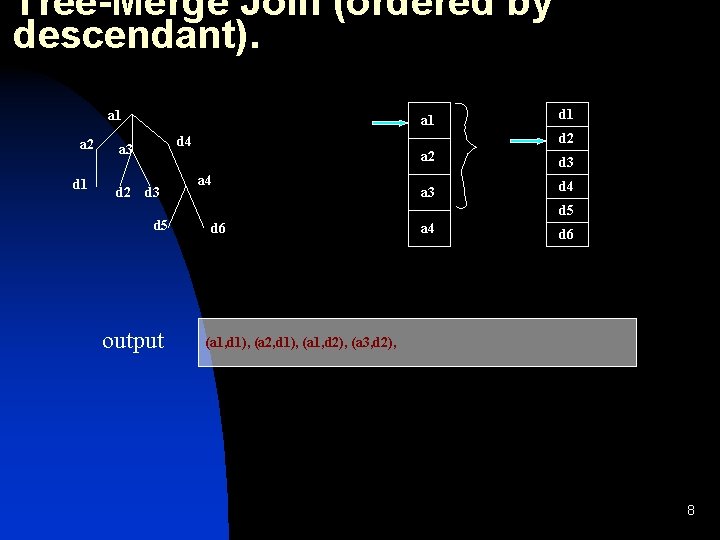
Tree-Merge Join (ordered by descendant). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), 8

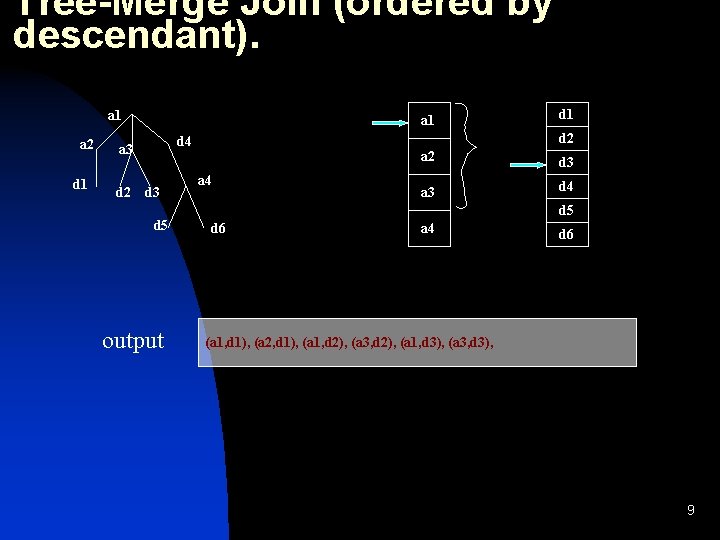
Tree-Merge Join (ordered by descendant). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), 9

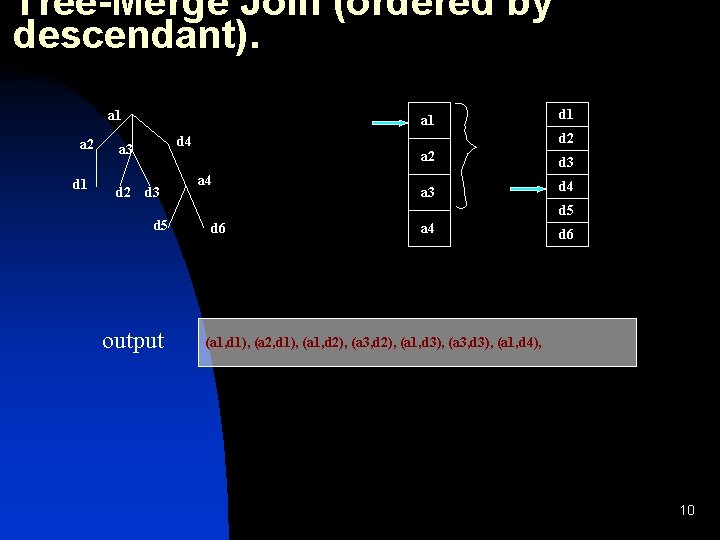
Tree-Merge Join (ordered by descendant). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), (a 1, d 4), 10

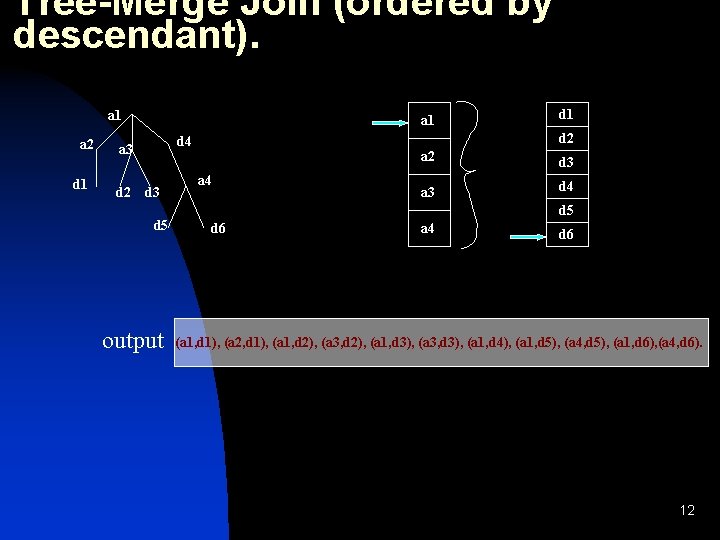
Tree-Merge Join (ordered by descendant). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), (a 1, d 4), (a 1, d 5), (a 4, d 5), 11

Tree-Merge Join (ordered by descendant). a 1 a 2 d 1 a 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), (a 1, d 4), (a 1, d 5), (a 4, d 5), (a 1, d 6), (a 4, d 6). 12

Which is more efficient? n n n Tree-Merge-anc: time and space complexity – O(|Alist| + |Dlist| + |Output. List|). Note: it is not quadratic in input size. However, Tree-Merge-desc has quadratic worst-case time complexity. u u Saw some evidence in previous example. Here is another “bad” input: a 0 a 1 What is amount of the work done by Tree-Merge-desc on this input? d 1 a 2 d 2 an dn 13

More analysis • What about finding (par, child) pairs? • Does the same upper bound apply for T-M-par? • Consider the input below. • The size of the o/p list is O(|Alist| + |Dlist|). • What’s the amount of work done by T-M-par on this input? a 1 d 1 a 2 d 2 n-1 an A breed of stack-tree SJ algorithms have been developed to overcome the deficiencies of T-M algorithms. dn dn+1 14

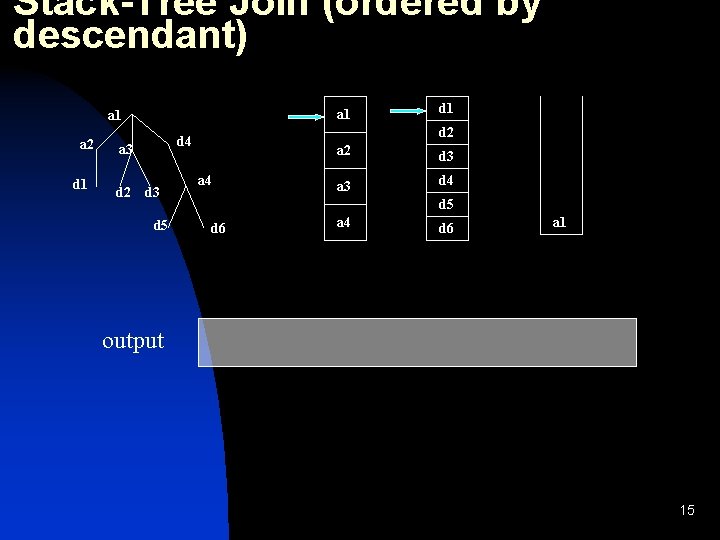
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 a 1 output 15

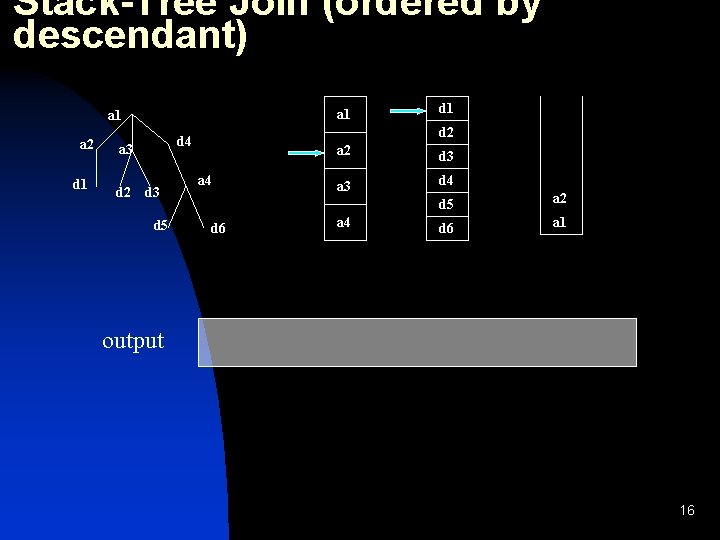
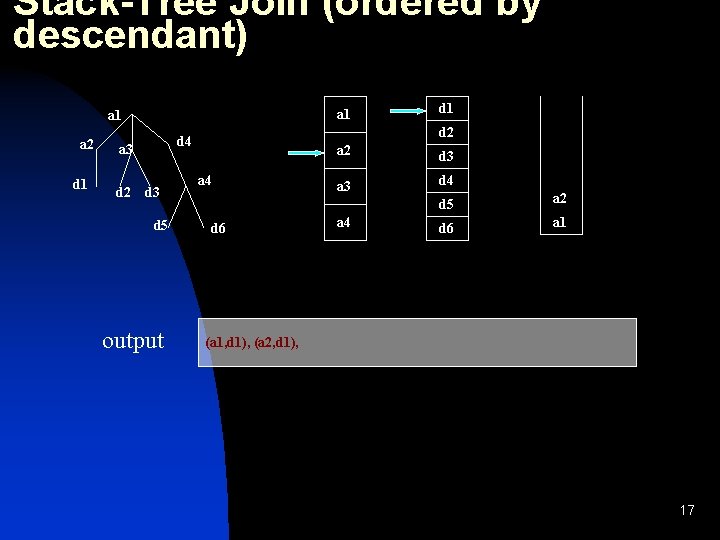
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 2 d 6 a 1 output 16

Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 2 d 6 a 1 (a 1, d 1), (a 2, d 1), 17

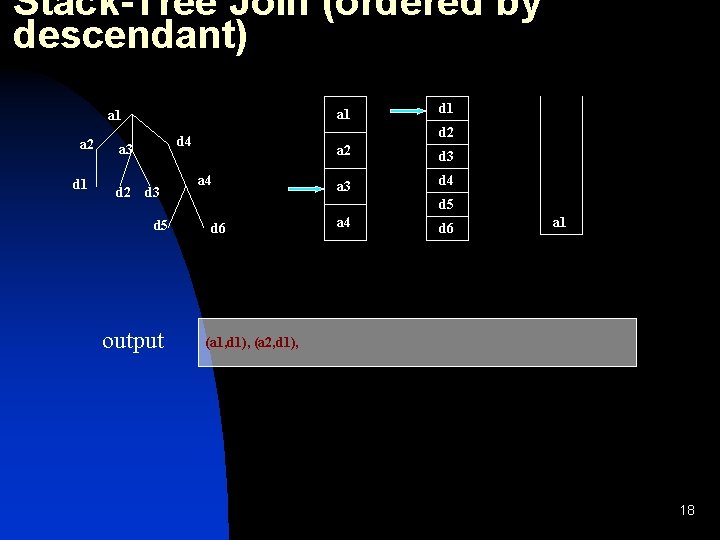
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 a 1 (a 1, d 1), (a 2, d 1), 18

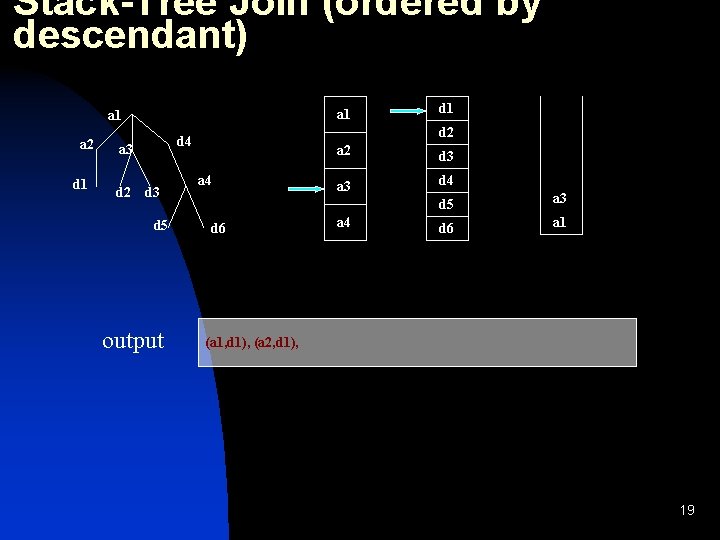
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 3 d 6 a 1 (a 1, d 1), (a 2, d 1), 19

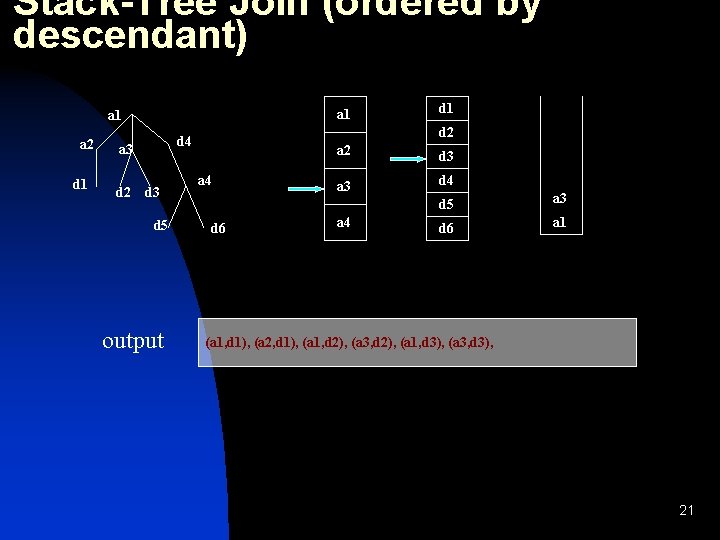
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 3 d 6 a 1 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), 20

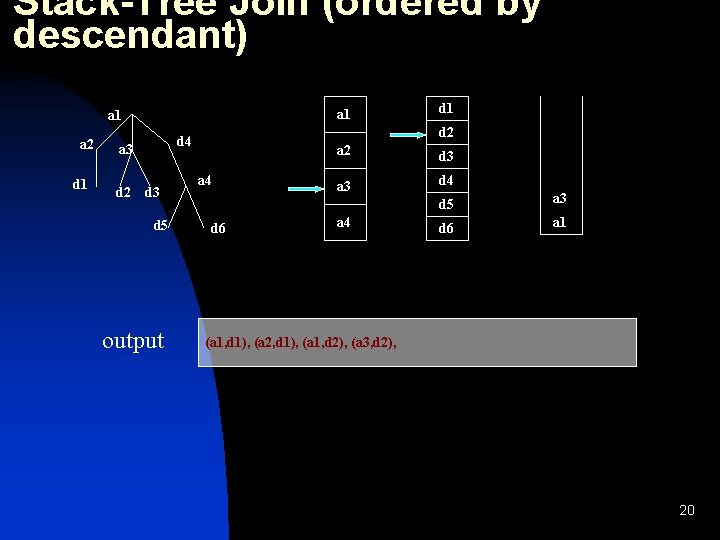
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 3 d 6 a 1 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), 21

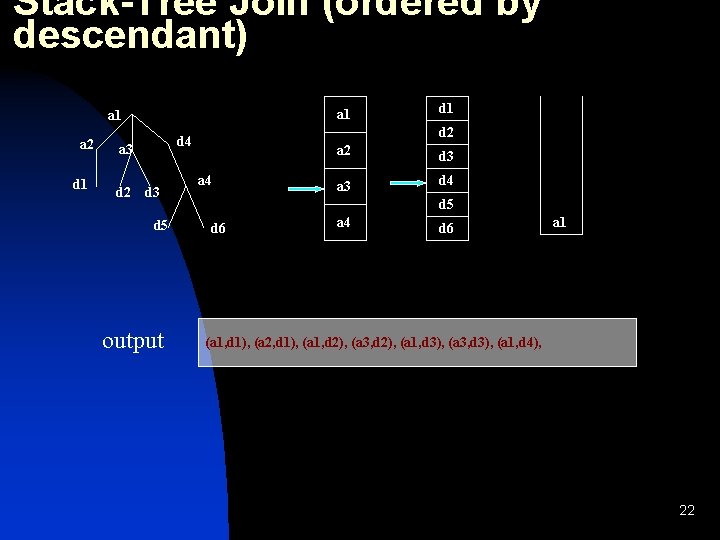
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 a 2 d 3 a 3 d 4 d 5 d 6 a 4 d 6 a 1 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), (a 1, d 4), 22

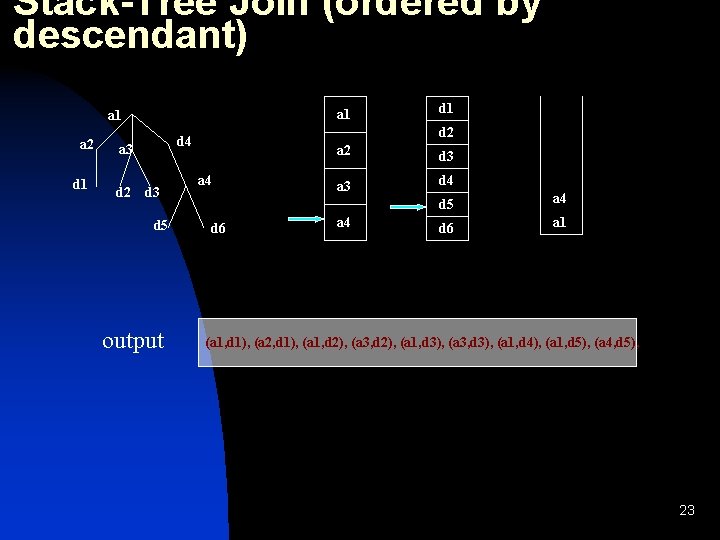
Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 4 d 6 a 1 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), (a 1, d 4), (a 1, d 5), (a 4, d 5), 23

Stack-Tree Join (ordered by descendant) a 1 a 2 d 1 d 2 d 4 a 3 d 5 output d 1 a 4 d 6 a 2 d 3 a 3 d 4 a 4 d 5 a 4 d 6 a 1 (a 1, d 1), (a 2, d 1), (a 1, d 2), (a 3, d 2), (a 1, d 3), (a 3, d 3), (a 1, d 4), (a 1, d 5), (a 4, d 5), (a 1, d 6), (a 4, d 6). • Time & space complexity: O(|Alist| + |Dlist| + |Outputlist|). (for both ad and pc relationships!) • Unlike T-M-anc, I/O complexity is similarly bounded (modulo blocking factor). • Can handle streaming i/p lists: non-blocking algorithm. 24 • Stack-Tree-anc is similar with similar bounds.

Extensions n n n Can you adapt the SJ algorithms to handle SJ variants mentioned before? Can you make the Tree-Merge algorithms more efficient, e. g. , by bookkeeping? We have seen, a TPQ = a sequence of joins on the results of SJs; what’s the best way to order these joins? Can we reuse join order optimization from relational DB optimization? (what’s a right cost model? ) What if (universal) quantifiers are present? How can we handle aggregation? 25