Structural Equation Modeling SEM By Ahlam Lee Contents

Structural Equation Modeling (SEM) By Ahlam Lee

Contents • Concepts of SEM • Criteria for determining model fit 1) Absolute fit indices 2) Incremental fit indices • Software R install and codebook. • Research Example • Software R demonstration

Concepts of SEM • Structural Equation Modeling (SEM) is a multivariate statistical technique that can show structural relationships between variables. • SEM is used to test how well an existing theory fits into the sample data (your data). 1) Confirmatory factor analysis (it include only latent variables) 2) Path analysis (it includes only observed variables) 3) A general structural equation model that combines both confirmatory factor analysis and path analysis. Namely it includes both latent and observed variables.

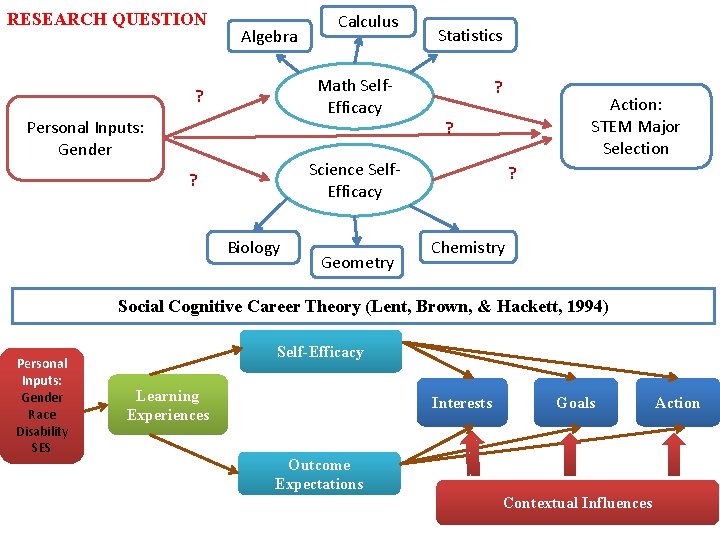
RESEARCH QUESTION Algebra Calculus Math Self. Efficacy ? Personal Inputs: Gender Statistics ? Action: STEM Major Selection ? Science Self. Efficacy ? Biology Geometry ? Chemistry Social Cognitive Career Theory (Lent, Brown, & Hackett, 1994) Personal Inputs: Gender Race Disability SES Self-Efficacy Learning Experiences Interests Goals Outcome Expectations Contextual Influences Action

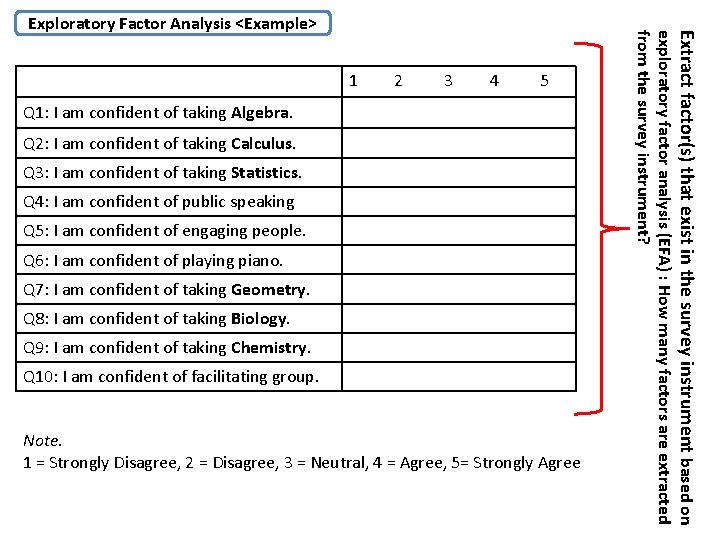
1 2 3 4 5 Q 1: I am confident of taking Algebra. Q 2: I am confident of taking Calculus. Q 3: I am confident of taking Statistics. Q 4: I am confident of public speaking Q 5: I am confident of engaging people. Q 6: I am confident of playing piano. Q 7: I am confident of taking Geometry. Q 8: I am confident of taking Biology. Q 9: I am confident of taking Chemistry. Q 10: I am confident of facilitating group. Note. 1 = Strongly Disagree, 2 = Disagree, 3 = Neutral, 4 = Agree, 5= Strongly Agree Extract factor(s) that exist in the survey instrument based on exploratory factor analysis (EFA) : How many factors are extracted from the survey instrument? Exploratory Factor Analysis <Example>

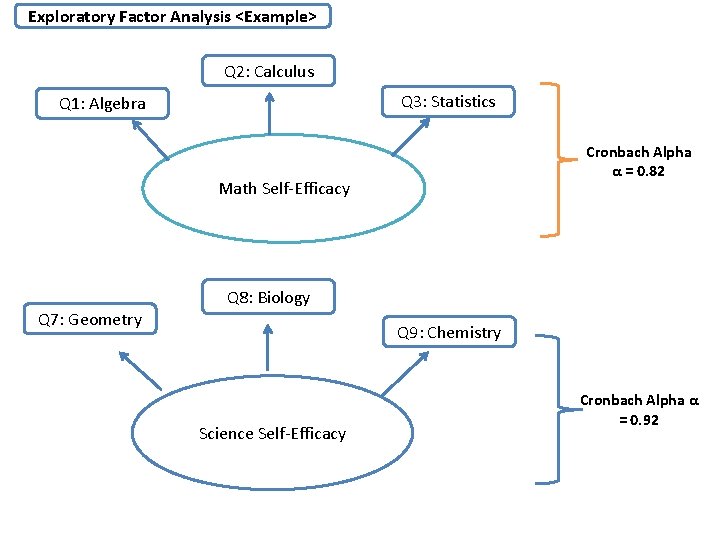
Exploratory Factor Analysis <Example> Q 2: Calculus Q 3: Statistics Q 1: Algebra Cronbach Alpha α = 0. 82 Math Self-Efficacy Q 8: Biology Q 7: Geometry Q 9: Chemistry Science Self-Efficacy Cronbach Alpha α = 0. 92

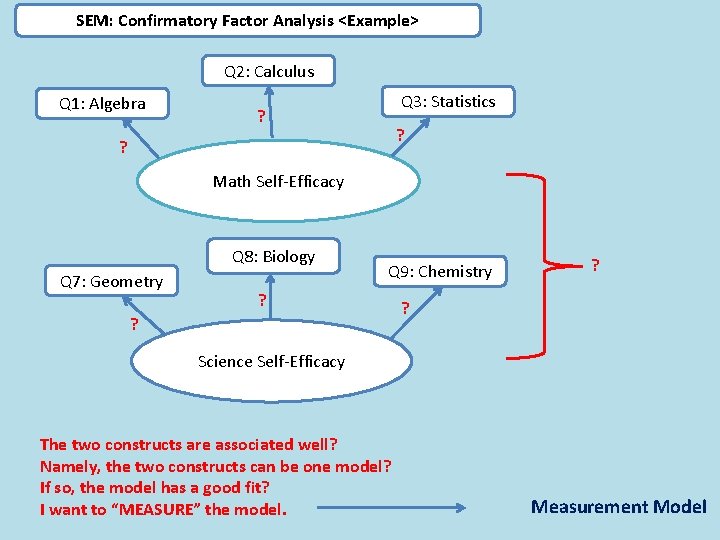
SEM: Confirmatory Factor Analysis <Example> Q 2: Calculus Q 1: Algebra Q 3: Statistics ? ? ? Math Self-Efficacy Q 8: Biology Q 7: Geometry Q 9: Chemistry ? ? Science Self-Efficacy The two constructs are associated well? Namely, the two constructs can be one model? If so, the model has a good fit? I want to “MEASURE” the model. Measurement Model

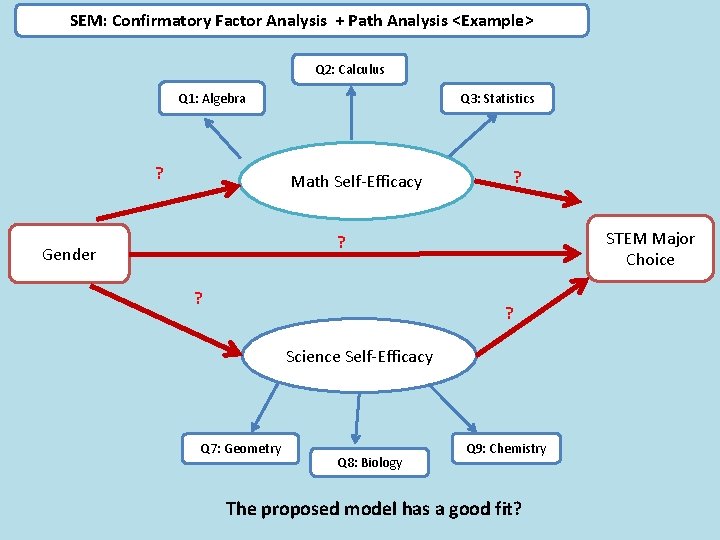
SEM: Confirmatory Factor Analysis + Path Analysis <Example> Q 2: Calculus Q 1: Algebra ? Q 3: Statistics Math Self-Efficacy ? STEM Major Choice ? Gender ? ? Science Self-Efficacy Q 7: Geometry Q 8: Biology Q 9: Chemistry The proposed model has a good fit?

Absolute fit indices for determining model fit • Absolute fit indices determine how well an existing theory or model fits the sample data and demonstrate whether a proposed model has a good model fit. Absolute Fit Indices 1) Model Chi-Square (X 2) 2) Root mean square error of approximation (RMSEA) RMSEA <= 0. 5: Close approximate fit 0. 5 < RMSEA < 0. 8: reasonable error of approximation 3) Goodness-of-fit statistic (GFI) and the adjusted goodness-offit statistic (AGFI) 4) Root mean square residual (RMR) and standardised root mean square residual (SRMR) SRMR < 0. 05: Well-fitting model SRMR < 0. 08: Acceptable criteria

Absolute fit indices for determining model fit 1) Model Chi-Square (X 2) Absolute Fit Indices 1) Model Chi-Square (X 2) Description It is the traditional measure for evaluating overall model fit and, ‘assess the magnitude of discrepancy between the sample and fitted covariances matrices’ (Hu & Bentler, 1992, page 2). Good model fit provides an insignificant result at the significance level of 0. 05 (Barrett, 2007). HOWEVER, there a number of limitations in its use. 1) It is sensitive to sample size, which means that the Chi-Square statistic nearly always rejects the model when large samples are used (Bentler & Bonnet, 1980; Jöreskog & Sörbom, 1983). On the other hand, where small samples are used, the Chi-Square statistic lacks power and may not discriminate between good fitting models and poor fitting models (Kenny & Mc. Coach, 2003). 2) This test assumes multivariate normality and thus, severe deviations from normality may result in model rejections even when the model is properly specified (Mclntosh, 2006). Due to the limitation of using the Model Chi-Square, researchers have sought alternative indices to assess model fit. One example of a statistic that minimizes the impact of sample size is relative/normed chi-square (X 2/df) (Wheaton et al. , 1977). • X 2/df > 5. 0 (Wheaton et al. , 1977) • X 2/df > 2. 0 (Tabachnick & Fidell, 2007) But, there is no consensus regarding an acceptable ratio for this statistic.

Absolute fit indices for determining model fit 2) Root mean square error of approximation (RMSEA) and 3) GFI & AGFI Absolute fit indices 2) RMSEA Description • • 3) Goodness-of-fit statistic (GFI) and the adjusted goodness-of-fit statistic (AGFI) First developed by Steiger and Lind (1980, cited in Steiger, 1990) It tells us how well the proposed model would fit the population covariance matrix (Byrne, 1998). Simply put, it measures the difference between the proposed and hypothetical (population) model. One of the most informative indices in SEM Criteria (cut-off points) RMSEA = 0: Exact/Perfect Fit RMSEA < 0. 05: Close Fit 0. 5 < RMSEA < 0. 08: Reasonable error of approximation/Mediocre Fit RMSEA >= 0. 10: Poor fit GFI and AGFI are ranged from 0 to 1. The closer the value to 1, the better the model fit. • Criteria (cut-off point) of GFI: a value of 0. 90 has been recommended, but when factor loading and sample sizes are low, a higher cut-off of 0. 95 is more appropriate (Miles & Shevlin, 1998). Given the sensitivity of this index, it has become less popular in recent years and it has even been recommended not to be used (Sharma et al. , 2005). • Criteria (cut-off point) of AGFI: a value of 0. 90 or above indicates well fitting model. Note that AGFI adjusts the GFI based on degrees of freedom. HOWEVER, these two indices are not often used due to the detrimental effect of sample size.

Absolute fit indices for determining model fit 4) Root mean square residual (RMR) and standardised root mean square residual (SRMR) Absolute Fit Indices RMR and SRMR Description • RMR and SRMR refer to the square root of the difference between the residuals of the sample covariance matrix and the hypothesized covariance matrix. • The RMR value is computed based on the scales of variables (e. g. , survey questionnaires) and it varies depending on the scale range (e. g. , some survey questionnaires are ranged from 1 -5 while others range from 1 -7). Thus, it becomes difficult to interpret (Kline, 2005). • However, the standardized RMR (SRMR) resolves this problem and it is much more recommended to be used. • A SRMR of 0: Perfect fit • SRMR range from 0 to 1, with well fitting models obtaining values less than 0. 05 (Byrne, 1998; Diamantopoulos & Siguaw, 2000). However, a cut-off of 0. 08 are deemed acceptable (Hu & Bentler, 1999).

Incremental fit indices for determining model fit • • Incremental fit indices are also known as comparative or relative fit indices. Incremental fit indices are a group of indices that compare the chi-square value to a baseline model. Incremental Fit Indices Description Comparative Fit Indexes (CFI) • • Normed-fit index (NFI) • It is the most widely used in SEM. It assesses the relative improvement in it of the researcher’s model compared with a baseline model. • Cut-off criteria: a value of CFI >=0. 90 is considered a good fit (Hu & Bentler, 1999). However, a cut-off criterion of CFI >=0. 95 is more preferred. Note: It ranges from 0 to 1. Cut-off criteria: a value greater than 0. 90 is considered a good fit (Bentler & Bonnet, 1980. However, just like CFI criteria, a cut-off criterion of NFI >=0. 95 is more preferred. Note: it ranges from 0 to 1. • This index is sensitive to sample size, which underestimates fit for samples less than 200 (Mulaik et al. , 1989; Bentler, 1990). Thus, it does not recommended to be solely relined on (Kline, 2005).

Software R Please watch the following youtube video The installation process of Window and Mac is similar, but I put the You. Tube video for both types of computers. • For Window https: //www. youtube. com/watch? v=e. D 07 Nzngu. A 4 “Install R and RStudio on Windows 7 (Open. Intro)” • For Mac https: //www. youtube. com/watch? v=PHi-6 GWf. MBQ&nohtml 5=False “Download and Installing R and Rstudio on Mac and Windows”

Using R software, we will develop 1) SEM model based on confirmatory factor analysis; and 2) SEM model based on confirmatory factor analysis and path analysis. SEE the next slides and OPEN the R Studio and R syntax file (R syntax file_SEM_Session 12. txt).

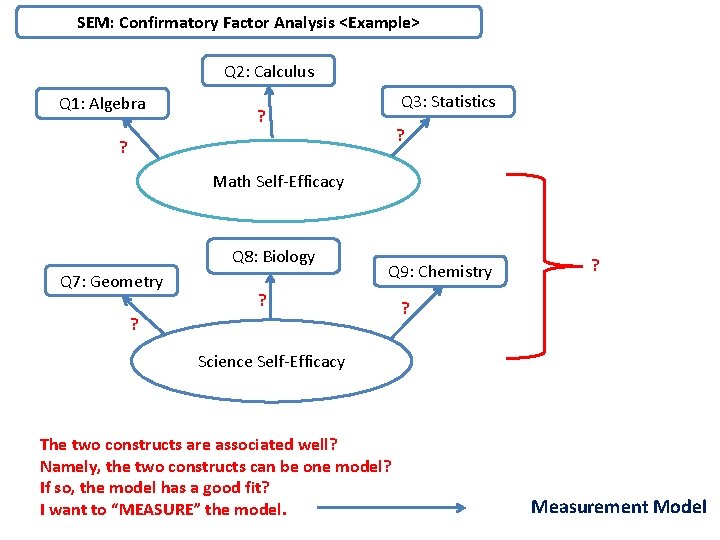
SEM: Confirmatory Factor Analysis <Example> Q 2: Calculus Q 1: Algebra Q 3: Statistics ? ? ? Math Self-Efficacy Q 8: Biology Q 7: Geometry Q 9: Chemistry ? ? Science Self-Efficacy The two constructs are associated well? Namely, the two constructs can be one model? If so, the model has a good fit? I want to “MEASURE” the model. Measurement Model

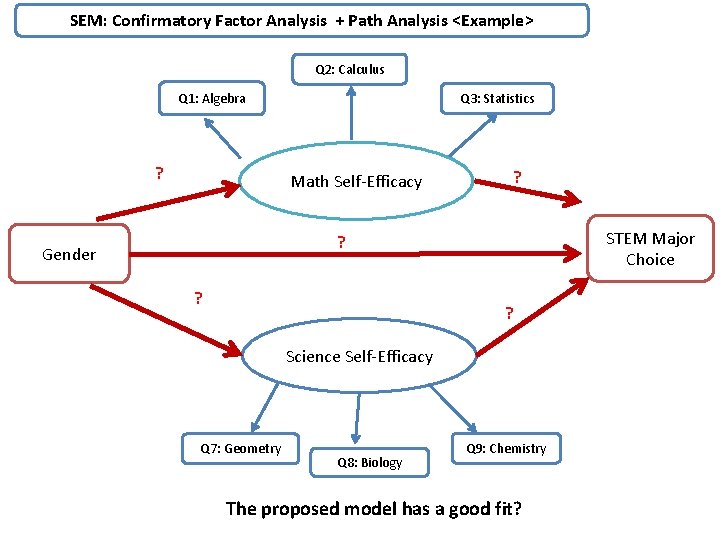
SEM: Confirmatory Factor Analysis + Path Analysis <Example> Q 2: Calculus Q 1: Algebra ? Q 3: Statistics Math Self-Efficacy ? STEM Major Choice ? Gender ? ? Science Self-Efficacy Q 7: Geometry Q 8: Biology Q 9: Chemistry The proposed model has a good fit?

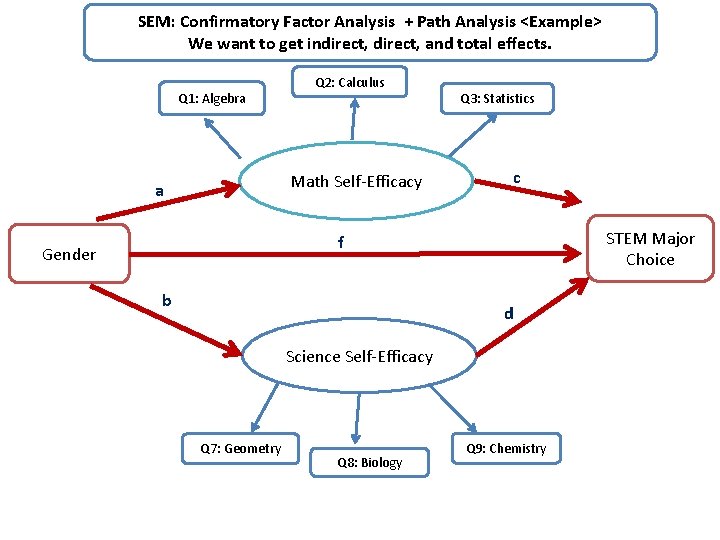
SEM: Confirmatory Factor Analysis + Path Analysis <Example> We want to get indirect, and total effects. Q 1: Algebra Q 2: Calculus Math Self-Efficacy a Q 3: Statistics c STEM Major Choice f Gender b d Science Self-Efficacy Q 7: Geometry Q 8: Biology Q 9: Chemistry

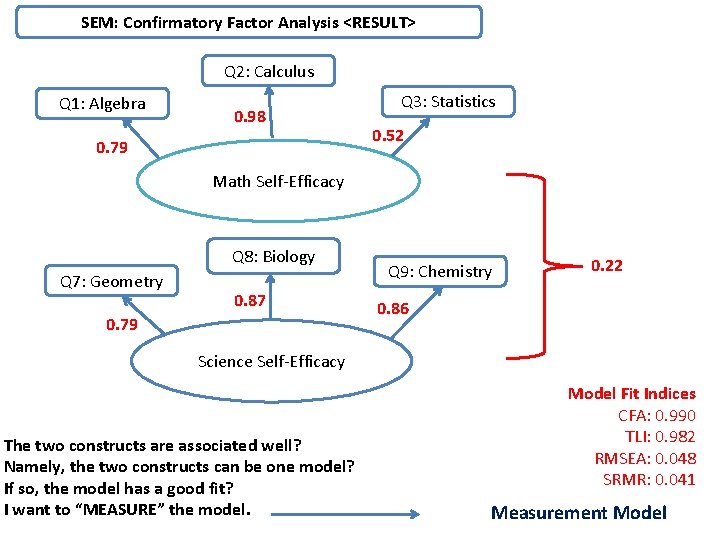
SEM: Confirmatory Factor Analysis <RESULT> Q 2: Calculus Q 1: Algebra 0. 98 0. 79 Q 3: Statistics 0. 52 Math Self-Efficacy Q 8: Biology Q 7: Geometry 0. 87 0. 79 Q 9: Chemistry 0. 22 0. 86 Science Self-Efficacy The two constructs are associated well? Namely, the two constructs can be one model? If so, the model has a good fit? I want to “MEASURE” the model. Model Fit Indices CFA: 0. 990 TLI: 0. 982 RMSEA: 0. 048 SRMR: 0. 041 Measurement Model

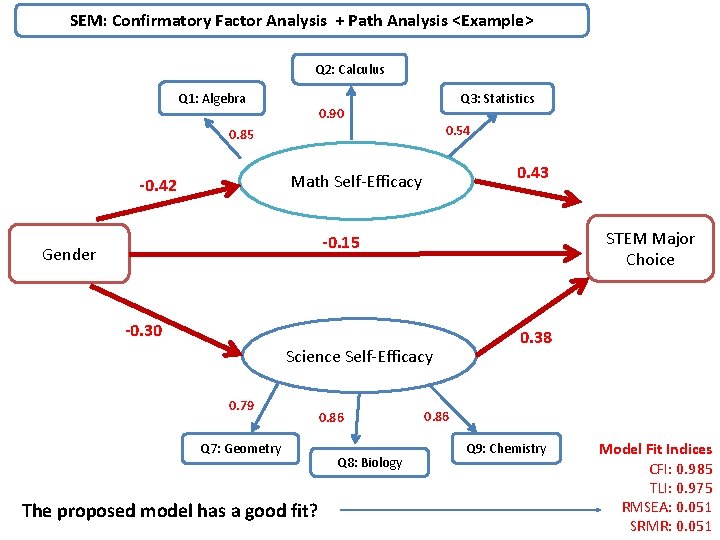
SEM: Confirmatory Factor Analysis + Path Analysis <Example> Q 2: Calculus Q 1: Algebra Q 3: Statistics 0. 90 0. 54 0. 85 0. 43 Math Self-Efficacy -0. 42 STEM Major Choice -0. 15 Gender -0. 30 Science Self-Efficacy 0. 79 Q 7: Geometry The proposed model has a good fit? 0. 86 Q 8: Biology 0. 38 0. 86 Q 9: Chemistry Model Fit Indices CFI: 0. 985 TLI: 0. 975 RMSEA: 0. 051 SRMR: 0. 051

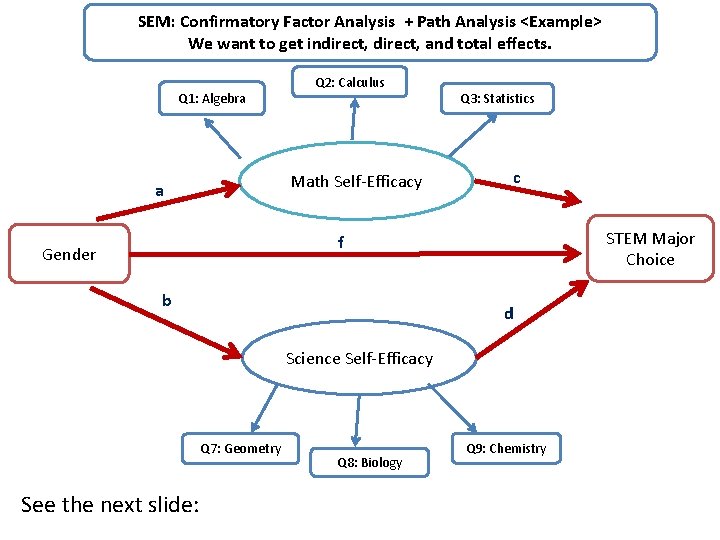
SEM: Confirmatory Factor Analysis + Path Analysis <Example> We want to get indirect, and total effects. Q 1: Algebra Q 2: Calculus Math Self-Efficacy a Q 3: Statistics c STEM Major Choice f Gender b d Science Self-Efficacy Q 7: Geometry See the next slide: Q 8: Biology Q 9: Chemistry

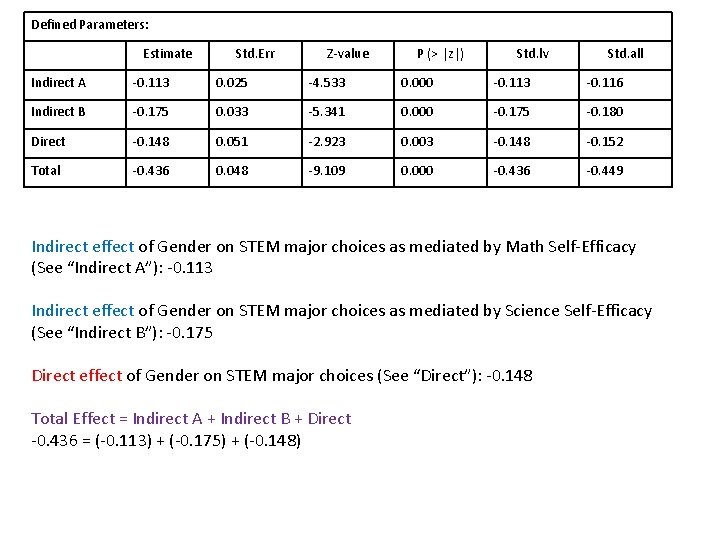
Defined Parameters: Estimate Std. Err Z-value P (> |z|) Std. lv Std. all Indirect A -0. 113 0. 025 -4. 533 0. 000 -0. 113 -0. 116 Indirect B -0. 175 0. 033 -5. 341 0. 000 -0. 175 -0. 180 Direct -0. 148 0. 051 -2. 923 0. 003 -0. 148 -0. 152 Total -0. 436 0. 048 -9. 109 0. 000 -0. 436 -0. 449 Indirect effect of Gender on STEM major choices as mediated by Math Self-Efficacy (See “Indirect A”): -0. 113 Indirect effect of Gender on STEM major choices as mediated by Science Self-Efficacy (See “Indirect B”): -0. 175 Direct effect of Gender on STEM major choices (See “Direct”): -0. 148 Total Effect = Indirect A + Indirect B + Direct -0. 436 = (-0. 113) + (-0. 175) + (-0. 148)