Structural Equation Modeling of Longitudinal Data Lee Sechrest

Structural Equation Modeling of Longitudinal Data Lee Sechrest (Mei-kuang Chen, & Patricia Herman) Special thanks to “The Partnership” in Tucson, AZ, for providing data for this presentation 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

Focus More of a demonstration of tools for longitudinal data than a communication of findings Structural equation modeling (latent growth curve) vs. multi-level modeling (or hierarchical modeling) Participants in substance treatment program A little bit about “How” Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, 11/12/2009 AEA

Data & Research Questions Data: Global Appraisal of Individual Needs (GAIN) data of justice-involved youth in the U. S. Southwest (Southern California, Arizona, New Mexico, & Southern Texas) from 1999 -2007, N=3047, 4 time points How did the youth in the substance treatment programs change over time? - in terms of self-reported substance use problem in the past month (SPSM) What characteristics can predict therapeutic change over time? 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

Data Analysis Structural equation modeling- large dataset Multi-level modeling Statistical package: SAS 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

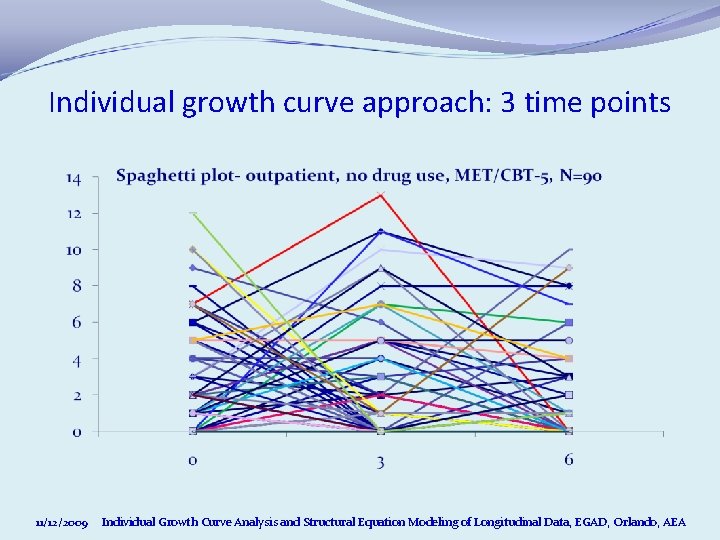
Individual growth curve approach: 3 time points 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

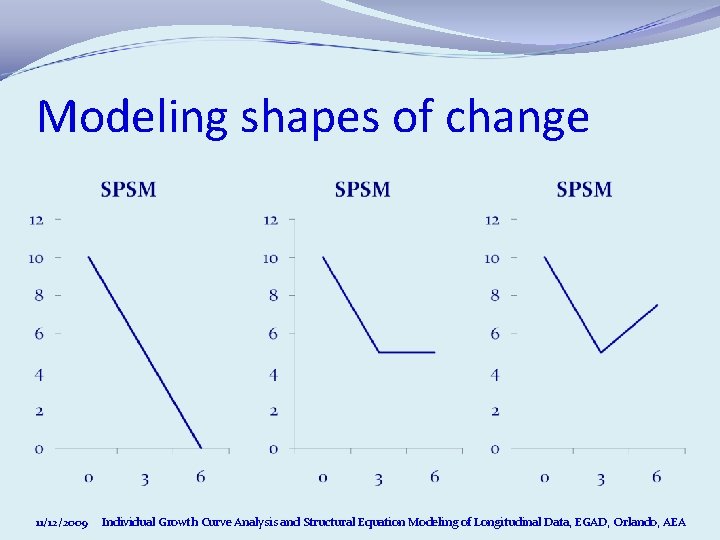
Modeling shapes of change 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

Structural Equation Modeling Latent growth curve- a sort of average of all the individual growth curves Practical decisions: Missing data issue Time variable- 0, 3, 6, and 12 months: sensitivity analysis Three models of different shapes for two complete datasets 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

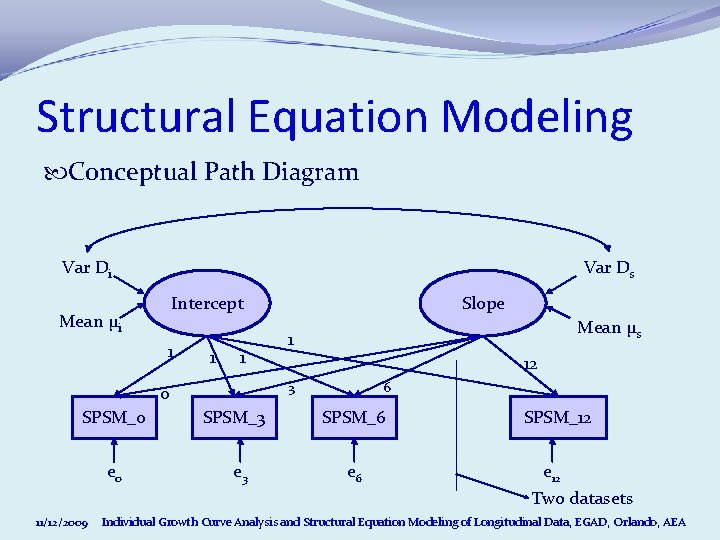
Structural Equation Modeling Conceptual Path Diagram Var Di Var Ds Intercept Mean μi 1 1 1 e 0 11/12/2009 Mean μs 1 12 3 0 SPSM_0 Slope SPSM_3 e 3 6 SPSM_6 e 6 SPSM_12 e 12 Two datasets Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

SAS code for latent growth curve proc calis ucov aug data=semppp 6 kurtosis; Lineqs spsm_0 = F 1 + 0 F 2 + E 1, spsm_3 = F 1 + 3 F 2 + E 2, spsm_6 = F 1 + 6 F 2 + E 3, F 1 = intcpt intercept + D 1, F 2 = slope intercept + D 2; Std E 1 -E 3 = E 0 E 3 E 6, D 1 -D 2 = Int Slp; Cov D 1 -D 2=Cor; Run; 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

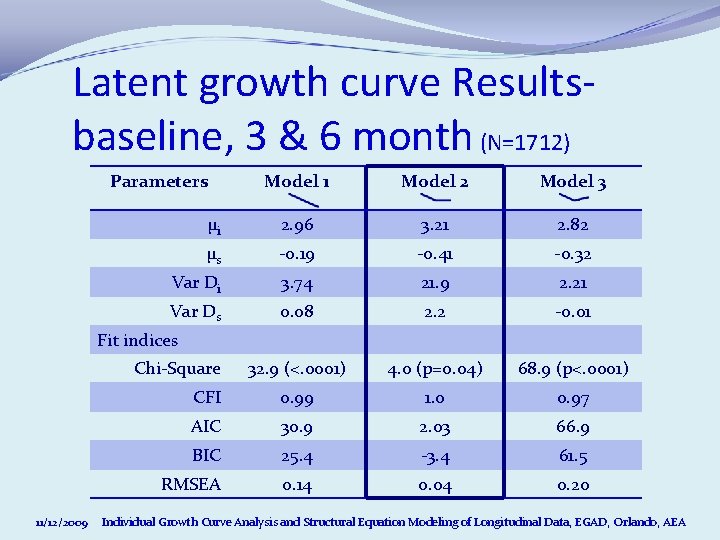
Latent growth curve Resultsbaseline, 3 & 6 month (N=1712) Parameters Model 1 Model 2 Model 3 μi 2. 96 3. 21 2. 82 μs -0. 19 -0. 41 -0. 32 Var Di 3. 74 21. 9 2. 21 Var Ds 0. 08 2. 2 -0. 01 32. 9 (<. 0001) 4. 0 (p=0. 04) 68. 9 (p<. 0001) CFI 0. 99 1. 0 0. 97 AIC 30. 9 2. 03 66. 9 BIC 25. 4 -3. 4 61. 5 RMSEA 0. 14 0. 04 0. 20 Fit indices Chi-Square 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

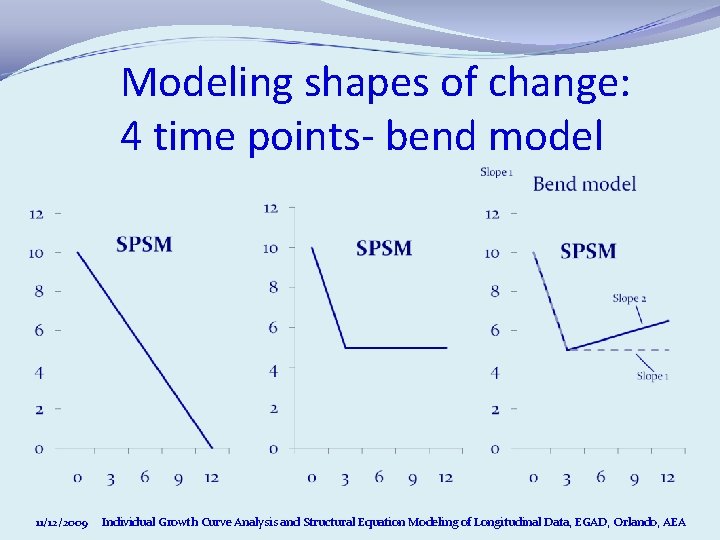
Modeling shapes of change: 4 time points- bend model 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

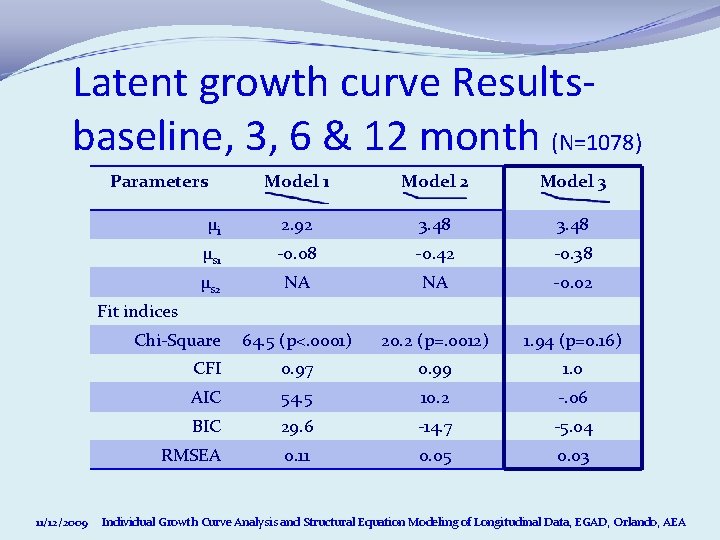
Latent growth curve Resultsbaseline, 3, 6 & 12 month (N=1078) Parameters Model 1 Model 2 Model 3 μi 2. 92 3. 48 μs 1 -0. 08 -0. 42 -0. 38 μs 2 NA NA -0. 02 64. 5 (p<. 0001) 20. 2 (p=. 0012) 1. 94 (p=0. 16) CFI 0. 97 0. 99 1. 0 AIC 54. 5 10. 2 -. 06 BIC 29. 6 -14. 7 -5. 04 RMSEA 0. 11 0. 05 0. 03 Fit indices Chi-Square 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

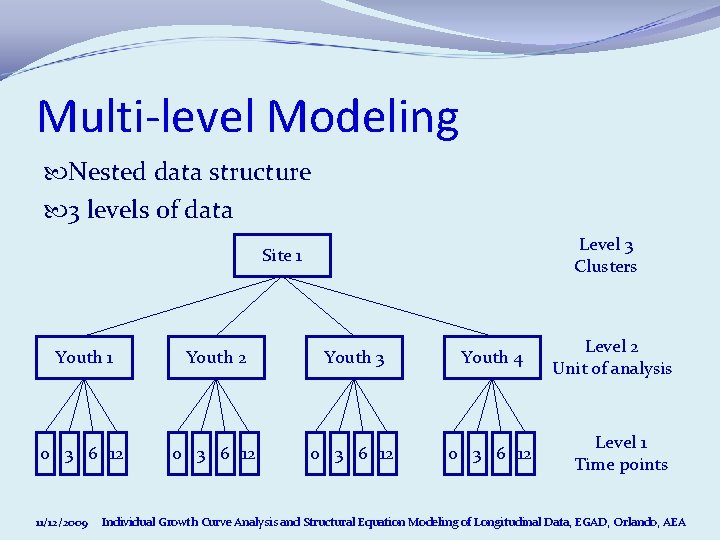
Multi-level Modeling Nested data structure 3 levels of data Level 3 Clusters Site 1 Youth 2 Youth 3 Youth 4 0 3 6 12 11/12/2009 Level 2 Unit of analysis Level 1 Time points Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

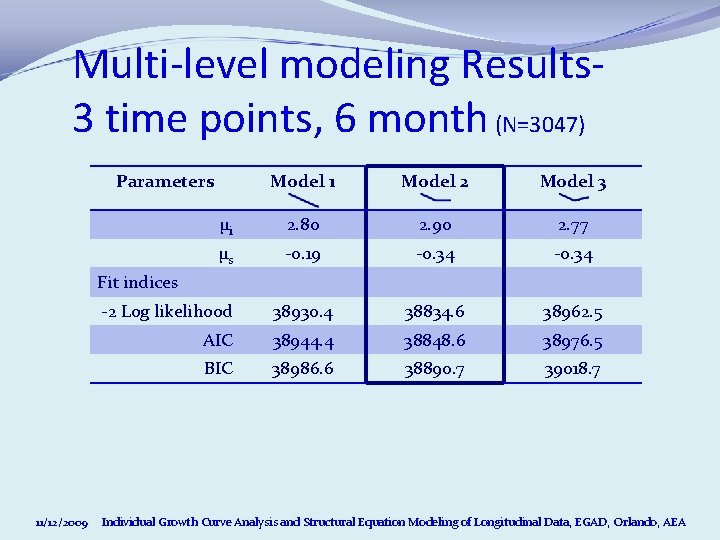
Multi-level modeling Results 3 time points, 6 month (N=3047) Parameters Model 1 Model 2 Model 3 μi 2. 80 2. 90 2. 77 μs -0. 19 -0. 34 -2 Log likelihood 38930. 4 38834. 6 38962. 5 AIC 38944. 4 38848. 6 38976. 5 BIC 38986. 6 38890. 7 39018. 7 Fit indices 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

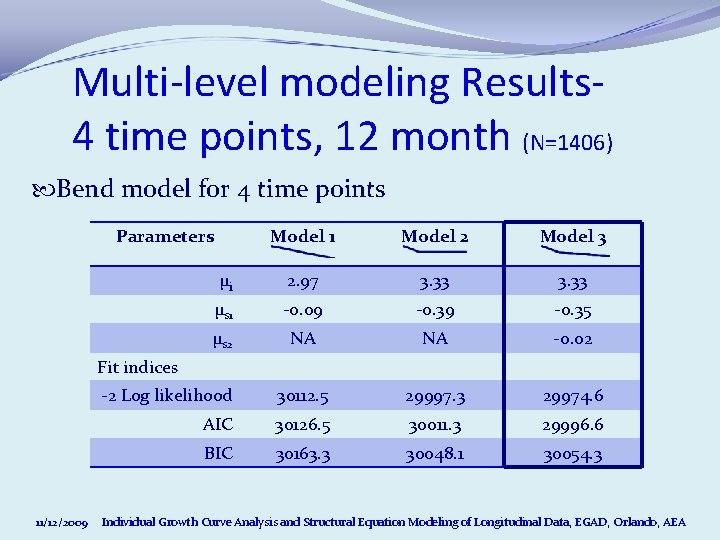
Multi-level modeling Results 4 time points, 12 month (N=1406) Bend model for 4 time points Parameters Model 1 Model 2 Model 3 μi 2. 97 3. 33 μs 1 -0. 09 -0. 35 μs 2 NA NA -0. 02 -2 Log likelihood 30112. 5 29997. 3 29974. 6 AIC 30126. 5 30011. 3 29996. 6 BIC 30163. 3 30048. 1 30054. 3 Fit indices 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

Comparison: latent growth curve and multi-level modeling Best model: Estimated parameters: best model Models SEM (3) SEM (4) HLM (3) HLM (4) μi 3. 21 3. 48 2. 90 3. 33 μs 1 -0. 41 -0. 38 -0. 34 -0. 35 μs 2 NA -0. 02 Missing data issues- different numbers of cases Unexpected pattern: who responded at 12 month? 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

Conclusion Choices of tools for longitudinal data analysis: preference and convenience Different strengths SEM- large dataset, strong theoretical understanding HLM: missing data, individual growth curve parameters Next step: predictors 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA

Reference Mc. Ardle, J. J. (2004). Latent growth curve analysis using structural equation modeling techniques. In D. M. Teti (ed. ), Handbook of Research Methods in Developmental Science. Blackwell Publishing, 2004. Blackwell Reference Online. 04 November 2009 <http: //www. blackwellreference. com/subscriber/tocn ode? id=g 9780631222618_chunk_g 978063122261819> West, B. , Welch, K. , & Galecki, A. (2006). Linear Mixed Models: A Practical Guide Using Statistical Software. First Edition. Baca Raton: Chapman Hall / CRC Press. 11/12/2009 Individual Growth Curve Analysis and Structural Equation Modeling of Longitudinal Data, EGAD, Orlando, AEA