Structural Design I Course Code CIVL 312 Dr

Structural Design I Course Code: CIVL 312 Dr. Aeid A. Abdulrazeg

Design of Reinforced Concrete Foundations �Foundations transfer loads from the building or individual columns to the earth. �Types of foundations are: 1. isolated bases for individual columns 2. combined bases for several columns 3. rafts for whole buildings which may incorporate basements

Isolated Bases Combined Bases Strip footing

Pile System Raft footing The type of foundation to be used depends on a number of factors such as 1. the soil properties and conditions 2. the type of structure and loading 3. the permissible amount of differential settlement

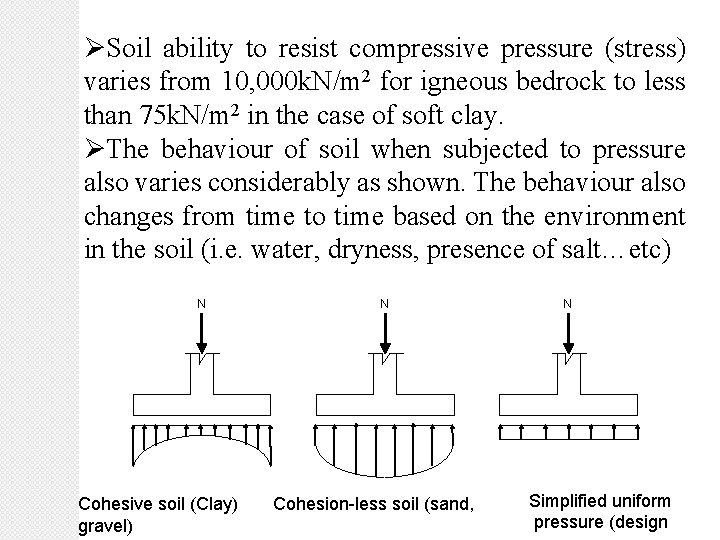
ØSoil ability to resist compressive pressure (stress) varies from 10, 000 k. N/m 2 for igneous bedrock to less than 75 k. N/m 2 in the case of soft clay. ØThe behaviour of soil when subjected to pressure also varies considerably as shown. The behaviour also changes from time to time based on the environment in the soil (i. e. water, dryness, presence of salt…etc) N Cohesive soil (Clay) gravel) N Cohesion-less soil (sand, N Simplified uniform pressure (design

Isolated Bases �Axially loaded footings In this case, uniform pressure is assumed to develop under the base of an axially loaded footing because the soil is uniformly compressed: Bearing pressure under the base of a footing is determined by treating the footing as a rigid element and the soil directly under the footing as a homogeneous elastic material that is isolated from the surrounding soil.

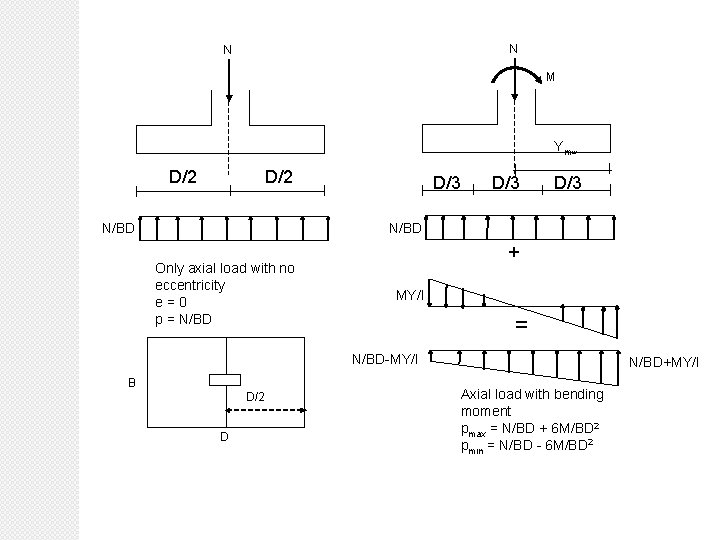
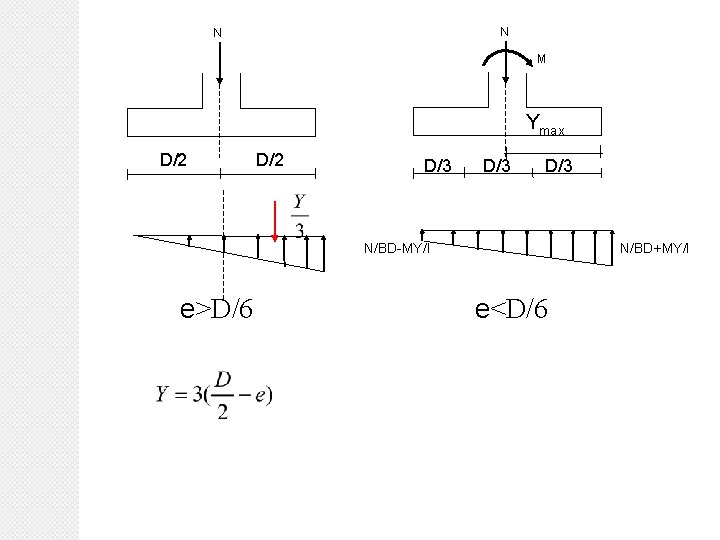
• Footing loaded with axial load and bending moment Moment may be caused by lateral forces due to wind or earthquake, by lateral soil pressure, or by eccentricity of column. Due to bending moment the pressure under the footing will not be uniform. In this case soil pressure can be determined by super imposing the direct stress due to axial load and bending stress due to moment. For c = D/2 (distance between the edge of the footing and the centreline of the column in the long direction) and I = BD 3/12: c/I = (D/2)/(BD 3/12) = 6/BD 2 and therefore Mc/I = 6 M/BD 2.

N N M Ym D/2 N/BD D/3 ax D/3 N/BD Only axial load with no eccentricity e=0 p = N/BD + MY/I = N/BD-MY/I B D/2 D N/BD+MY/I Axial load with bending moment pmax = N/BD + 6 M/BD 2 pmin = N/BD - 6 M/BD 2

N N M Ymax D/2 D/3 D/3 N/BD-MY/I e>D/6 N/BD+MY/I e<D/6

�Design � Axially of Isolated Bases loaded rectangular footing that supports a single column must be designed for punching shear, beam shear and bending moment. � This type of footings requires reinforcement in both directions because it bends in both directions (two-way action). To simplify design calculation an average effective depth d can be used for both directions. If the footing is square the analysis can be simplified by assuming its strength to be identical in both principal directions even though the actual effective depth is slightly different in each direction because a two-layer grid of steel is required

Punching shear A heavy load applied to the footing within a small area may cause a shear failure by pushing or punching out a pyramid around the column. This failure surface is caused by complex stress due to biaxial bending and biaxial compression. The code assumes that the failure occurs on a vertical surface located a distance 3 d/2 out from the face of the column. The perimeter of the failure surface is similar in shape to that of the column or of the loaded area. 3 d/2 Punching shear failure of pad footing Actual failure 3 d/2 Assumed failure Perimeter of failure surface d = effective depth of footing

Critical section for shear This section goes along a vertical section extending across the full width of the base. The code assumes this line lies at a distance equal to 1 d from the face of the column. Where d is the effective depth of the footing. Critical shear line in the long direction 1 d 1 d 1. 5 d Punching shear perimeter Maximum shear 1. 5 d Critical shear line in the short direction

Critical section for Bending The critical section for bending lies at the face of the column along the width and length of the base. Critical line for bending in the long direction Critical line for bending in the short direction

Shear at 1 d from the column faces X 1 d B D Where p= average pressure (stress) in this area.

B 1 d x D

Maximum shear lies at the face of the column. Shear stress at the face of column = < the lesser of 0. 8 or 5 N/mm 2. If not, change the section.

Example 1 The footing shown in Fig. is required to resist characteristic axial loads of 1000 k. N dead and 350 k. N imposed from a 400 mm square column. The safe bearing pressure on the soil is 200 k. N/ m 2 and the characteristic material strengths are fcu= 35 N/ mm 2 and fy= 460 N/ mm 2