Structural Coverage Verilog code is available to help

Structural Coverage • Verilog code is available to help generate tests o. Code can be analyzed statically and/or simulated • Easier to detect “additive” design errors o. Tests what the code actually does, not what it is supposed to do • Possible to automate test generation

Structural Coverage Metrics • • • Coverage metric is a numerical measurement of the adequacy of an arbitrary test set for verification. High coverage is a goal for test generation The measure is based on code execution 1. Toggle Coverage - Fraction of signals which have toggled 2. Statement coverage - Fraction of statements executed 3. Branch coverage - Fraction of branch directions executed 4. Path coverage - Fraction of control-flow paths executed

Toggle Coverage • Counts the fraction of signals/variables whose bits have toggled ex. x = 4 b 0000 and x=4 b 0111, 75% toggle coverage • Easy to compute • Little functional meaning (came from manufacturing/memory test)

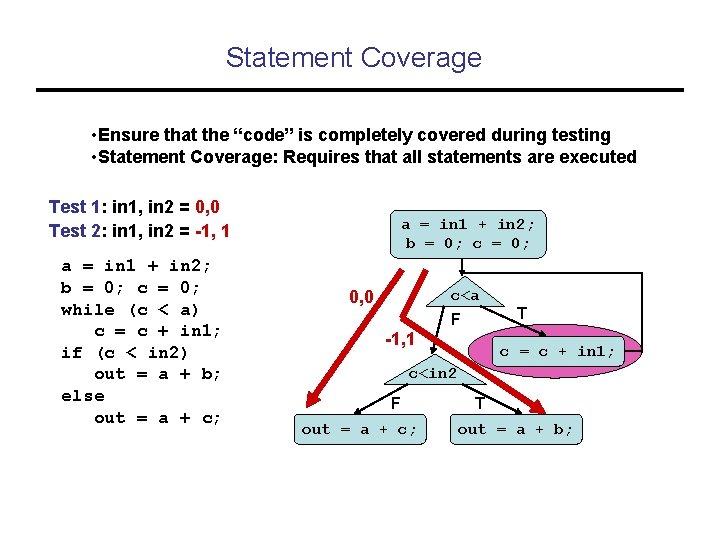
Statement Coverage • Ensure that the “code” is completely covered during testing • Statement Coverage: Requires that all statements are executed Test 1: in 1, in 2 = 0, 0 Test 2: in 1, in 2 = -1, 1 a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c<a 0, 0 T F -1, 1 c = c + in 1; c<in 2 F out = a + c; T out = a + b;

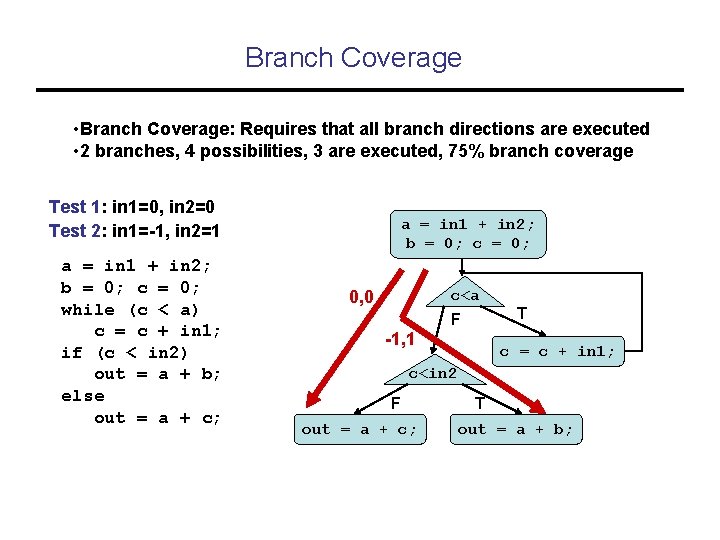
Branch Coverage • Branch Coverage: Requires that all branch directions are executed • 2 branches, 4 possibilities, 3 are executed, 75% branch coverage Test 1: in 1=0, in 2=0 Test 2: in 1=-1, in 2=1 a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c<a 0, 0 T F -1, 1 c = c + in 1; c<in 2 F out = a + c; T out = a + b;

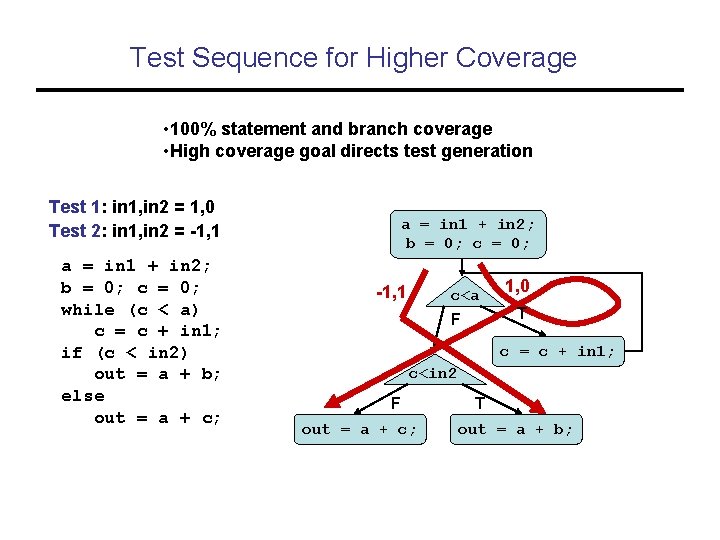
Test Sequence for Higher Coverage • 100% statement and branch coverage • High coverage goal directs test generation Test 1: in 1, in 2 = 1, 0 Test 2: in 1, in 2 = -1, 1 a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c = 0; -1, 1 c<a 1, 0 T F c = c + in 1; c<in 2 F out = a + c; T out = a + b;

Path Coverage • Each pattern covers a different control path • Infinite number of paths with a loop a = in 1 + in 2; b = 0; c = 0; -1, 1 c<a 0, 0 1, 0 T F c = c + in 1; c<in 2 F out = a + c; T out = a + b;

Domain (Boundary) Coverage • Each conditional predicate defines partitions the input space • A small error may move the partition foo (in 1, in 2) if (in 1 < in 2) out = 1; else out = 0; out=1 in 2 out=0 in 1 • What if in 1 < in 2 should be in 1 <= in 2? • What if in 1 or in 2 has a slightly incorrect value?

Domain Test Goal • Test with input data on the boundary and just on either side of the boundary foo (in 1, in 2) if (in 1 < in 2) out = 1; else out = 0; in 2 out=1 out=0 2 1 1 in 1 • Test 1: in 1, in 2 = 1, 1 - False, on the boundary • Test 2: in 1, in 2 = 1, 2 - True, just off the boundary

Domain Test Example • Need to satisfy 2 conditions for each predicate: q. True and on/near-boundary q. False and on/near-boundary a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; Test 1: in 1, in 2 = 0, 0 • Sets c = 0, and a = 0 • False and on-boundary for c < a • False and on-boundary for c < in 2 Test 2: in 1, in 2 = 1, 0 • Sets c = 0, and a = 0 • True and near-boundary for c < a • c set to 1 in loop • False and on-boundary for c < in 2 • 3 of 4 conditions satisfied, 75% coverage

Domain Test Complications • Non-standard Domain Boundaries Piecewise Linear Boundaries: Test each linear piece separately (in 2 > in 1) and (in 1 > 2) in 2 2 in 1 Higher Degree Boundaries: No standard solution (in 2 > in 12) in 2 in 1

Finite State Machine Metrics • These metrics assume that the HDL is written in an FSM style o. A ‘case’ statement which switches on a single ‘state’ var o. Each control path assigns the state variable case state is when 0 => x = 0; state = 3; when 1 => x = 1; state = 2; . . • State Coverage - All states are entered • Transition Coverage = All transitions are traversed

Optimism in a Coverage Metric • 100% statement coverage does not guarantee error detection • Test constraints may not be the same as detection constraints a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; Erroneous statement out = a - c; • Test 0, 0 executes erroneous statement but does not detect the error • Detection constraint includes a - c != a + c

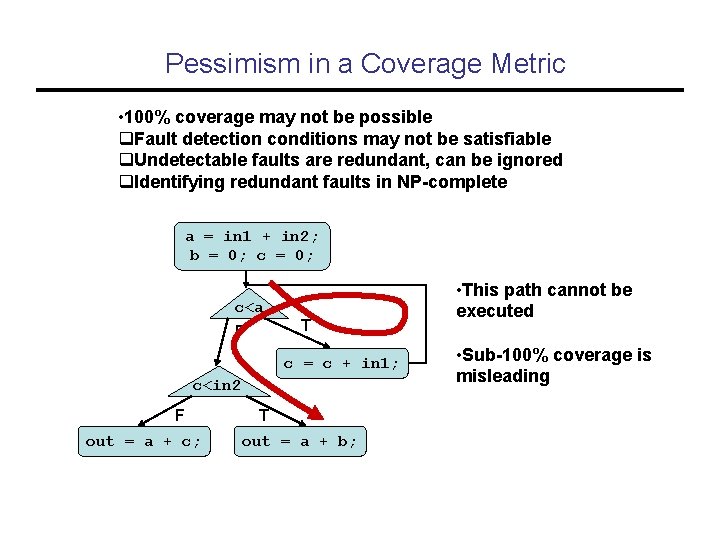
Pessimism in a Coverage Metric • 100% coverage may not be possible q. Fault detection conditions may not be satisfiable q. Undetectable faults are redundant, can be ignored q. Identifying redundant faults in NP-complete a = in 1 + in 2; b = 0; c<a T F c = c + in 1; c<in 2 F out = a + c; T out = a + b; • This path cannot be executed • Sub-100% coverage is misleading

Functional Coverage • Test goals are defined based on the features in the specification • The implementation (HDL) is not used to create tests • Coverage events are “interesting” events which might reveal errors • Coverage events must be defined manually because they are extracted from the specification Ex. Did overflow occur? Was x=17? Did an add follow a subtract?

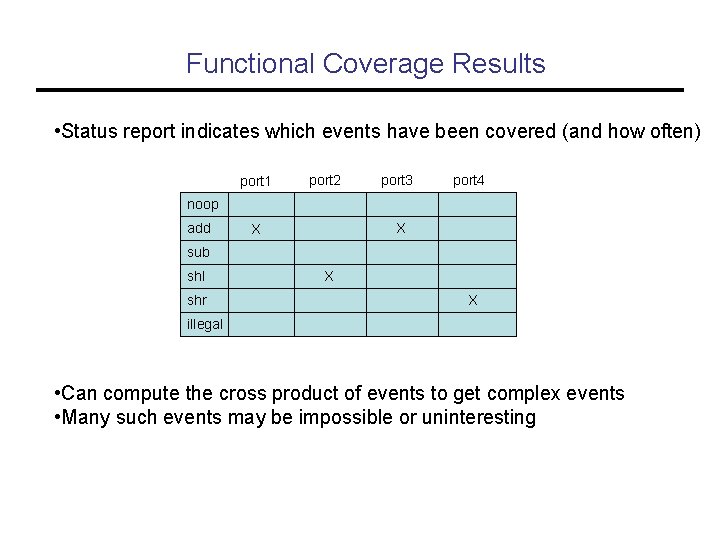
Functional Coverage Results • Status report indicates which events have been covered (and how often) port 1 port 2 port 3 port 4 noop add X X sub shl shr X X illegal • Can compute the cross product of events to get complex events • Many such events may be impossible or uninteresting