Structural Analysis and Design of Tubas Secondary School

Structural Analysis and Design of Tubas Secondary School By: Mosab Badran Nassar Sayed Abdullah Qawareeq Sohaib Mohammad Abu-Qubaita Supervisor : Eng. Ibrahim Arman 1

Graduation project content : � The preliminary dimension for elements such as slabs, beams and columns were analyzed using both hand calculations and verifications from sap. � The seismic base shear and wind loads were calculated and distributed all over the structural levels using UBC-97 and IBC-2012. � The snow load was determined using Jordanian code. 2

� The structural elements such as slabs, beams and columns were designed. � Footings were analyzed and designed using hand calculations and sap 2000. � The � Slab column interaction diagram was drawn. diaphragms and collectors were designed. 3

1. Introduction Description of the project � Tubas secondary school is located in Tubas city. � The school is composed of two parts, A and B. � Part A consists of three floors, part B consists of two floors. � The total area of structure is 2568 m 2. � floor height is 3. 38 m 4

1. Introduction Methodology - Preliminary design was calculated for every elements - A 3 D model was used for analysis and design considering gravity and lateral loads. Moreover, hand calculations were used for some elements for verification of the model. 5

1. Introduction Design codes and design method � The design was accomplished according to ACI 318 -2011 code, and IBC 2012 code. � UBC 97 and IBC 2012 was used for earthquake and wind loads � The ultimate strength method is used for structural design. � For seismic design both static and response spectrum methods were used. 6

1. Introduction Material Properties � Structural materials: Concrete of various strengths according to functions: � Beams, slabs and footings, f’c = 28 MPa. E = 2. 478 x 107 KN/m 2 � Columns f’c = 35 MPa, E = 2. 78 x 107 KN/m 2. � Unit weight of concrete, ϫ = 25 KN/ m 3. � Reinforcing Steel yielding strength, fy = 420 MPa, modulus of elasticity, E = 200 GPa. 7

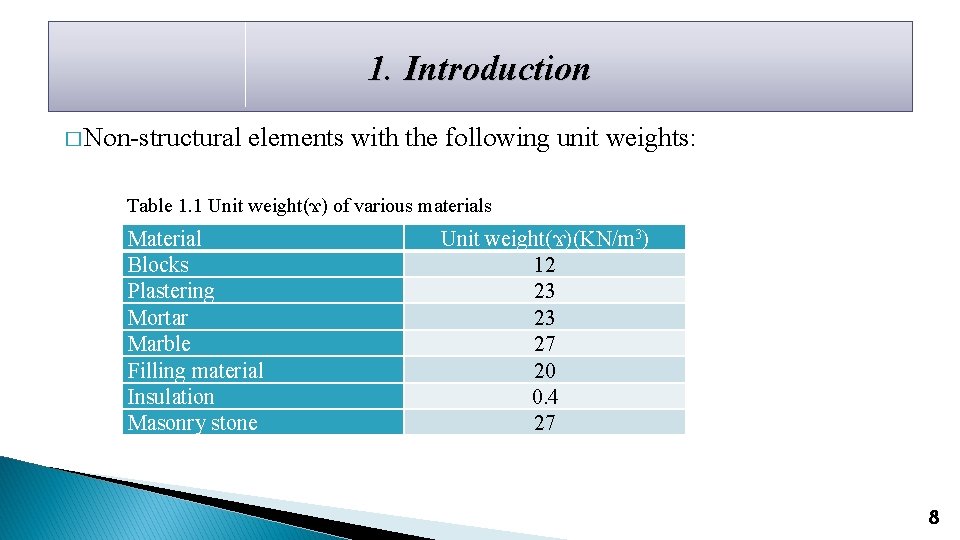
1. Introduction � Non-structural elements with the following unit weights: Table 1. 1 Unit weight(ϫ) of various materials Material Blocks Plastering Mortar Marble Filling material Insulation Masonry stone Unit weight(ϫ)(KN/m 3) 12 23 23 27 20 0. 4 27 8

1. Introduction Loads 1. Gravity loads 1) Dead loads: A. Own weight of structural elements. B. Super imposed dead load WSD = 5 KN/m 2 9

1. Introduction 2. Live loads: From IBC 2012 ( Table 1607. 1) as follows: � Classrooms = 1. 9 KN/m. � Corridors above first floor = 3. 83 KN/m 2. � First floor corridor = 4. 78 KN/m 2 According to UBC 97 code live load in classroom = 1. 9 KN/m 2 (table 16 -A). � As the schools in Palestine are used as emergency places, use live load. � WL = 5 KN/m 2. 10

1. Introduction 3. Horizontal loads � Seismic load and wind load that expected for the whole structure were computed according to IBC 2012 and UBC 97 as will be illustrated in Chapters 3 and 4. 11

1. Introduction Soil Properties � The site soil has an allowable bearing capacity of 330 KN/m 2. The soil is classified as rock soil. 12

2. Preliminary Design Introduction � Preliminary analysis and design of slabs, beams and columns based on gravity loads to determine the preliminary sizes of the different elements. � The building is composed of two parts, and each part was analyzed and designed individually. 13

2. Preliminary Design Building and slabs structural systems The building structural system is composed of 1 - Special shear walls 2 - Intermediate frames 14

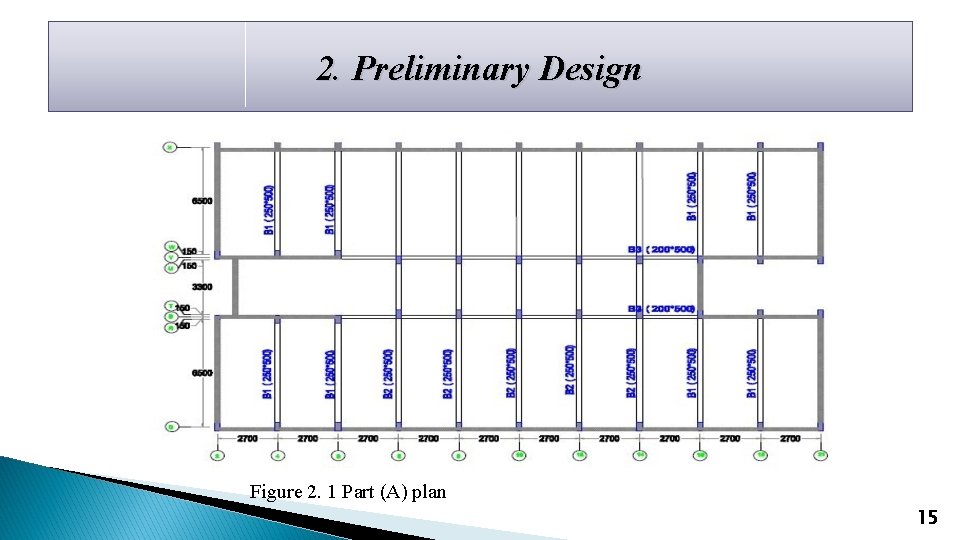
2. Preliminary Design Figure 2. 1 Part (A) plan 15

2. Preliminary Design � Table 9. 5(a) in ACI-318 code was used to compute thickness of beams and slabs. � Table 9. 5(b) in ACI-318 code was used to check deflection. � The deflection for every load was computed using sap and then compared with a value from table 9. 5(b) , the check was ok � Thickness of slab =150 mm � Depth of beam=500 mm 16

2. Preliminary Design � Dimensions for columns were found depending on the ultimate axial gravity load that subjected to, and according to this equation: � ФPn = 0. 8 Ф [0. 85 f'c (Ag-As) + Fy*As] � Ф= 0. 65 for tied columns � The dimensions of every column were 250 mm x 500 mm � The slab is one way solid in y-direction. 17

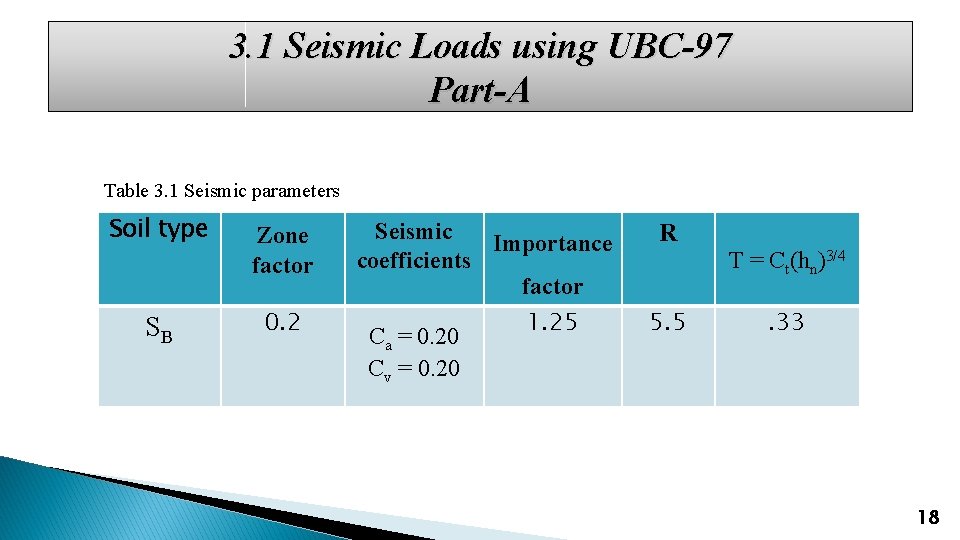
3. 1 Seismic Loads using UBC-97 Part-A Table 3. 1 Seismic parameters Soil type Zone factor SB 0. 2 Seismic Importance coefficients factor Ca = 0. 20 Cv = 0. 20 1. 25 R 5. 5 T = Ct(hn)3/4. 33 18

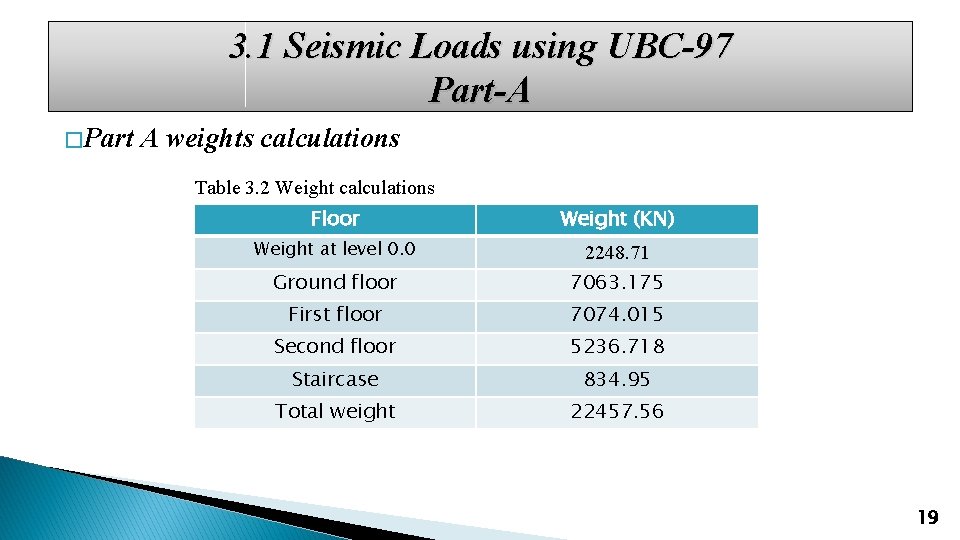
3. 1 Seismic Loads using UBC-97 Part-A � Part A weights calculations Table 3. 2 Weight calculations Floor Weight (KN) Weight at level 0. 0 Ground floor 2248. 71 7063. 175 First floor 7074. 015 Second floor 5236. 718 Staircase 834. 95 Total weight 22457. 56 19

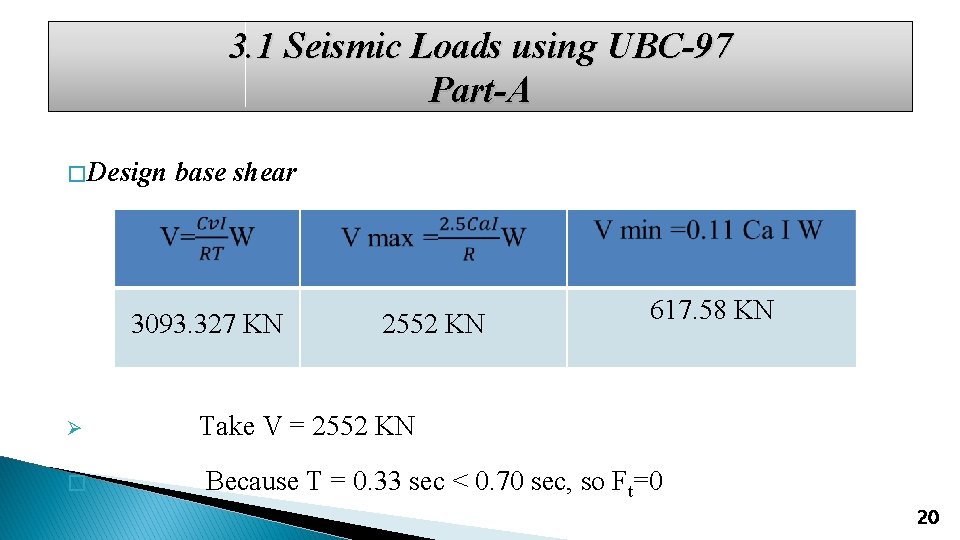
3. 1 Seismic Loads using UBC-97 Part-A � Design base shear 3093. 327 KN Ø � 2552 KN 617. 58 KN Take V = 2552 KN Because T = 0. 33 sec < 0. 70 sec, so Ft=0 20

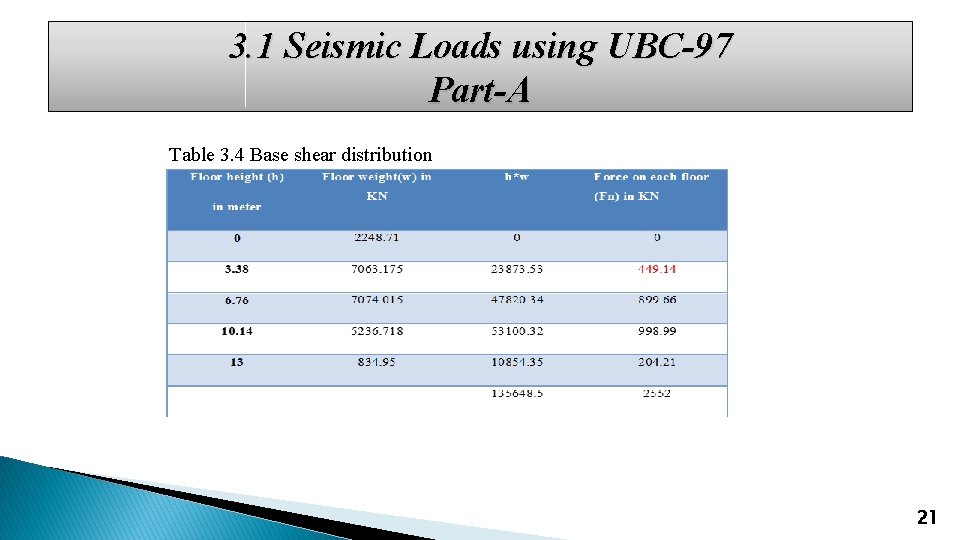
3. 1 Seismic Loads using UBC-97 Part-A Table 3. 4 Base shear distribution 21

3. 1 Seismic Loads using UBC-97 Part-B Table 3. 5 Base shear distribution Floor weight(w) height (h) in KN h*w Force on each floor (Fn) in KN in meter 0 1027. 55 0 0 3. 38 5837. 45 19730. 58 463. 99 6. 76 4325. 71 29241. 80 687. 66 8. 52 1383. 85 11790. 40 277. 27 60762. 78 Base shear =1428. 92 KN 1428. 92 22

3. 3 Seismic Loads using IBC-2012 Part-A Table 3. 6 Siesmic parameters Zone factor 0. 3 S 1=1. 25* Z 0. 375 Ss=1. 25*Z 0. 75 SDS=2/3 SMS SD 1 =2/3 SM 1 0. 5 0. 25 SMS = Fa Ss 0. 75 SM 1= FV S 1 0. 375 23

3. 3 Seismic Loads using IBC-2012 Part-A 24

3. 3 Seismic Loads using IBC-2012 Part-A �R = response modification factor � The value of R is 6 � Ie = importance factor = 1. 25 � Ta = 0. 0488 * 13. 75 = 0. 334 sec � The seismic base shear V � V =CSW = 0. 104 * 22457. 56 = 2335. 6 KN 25

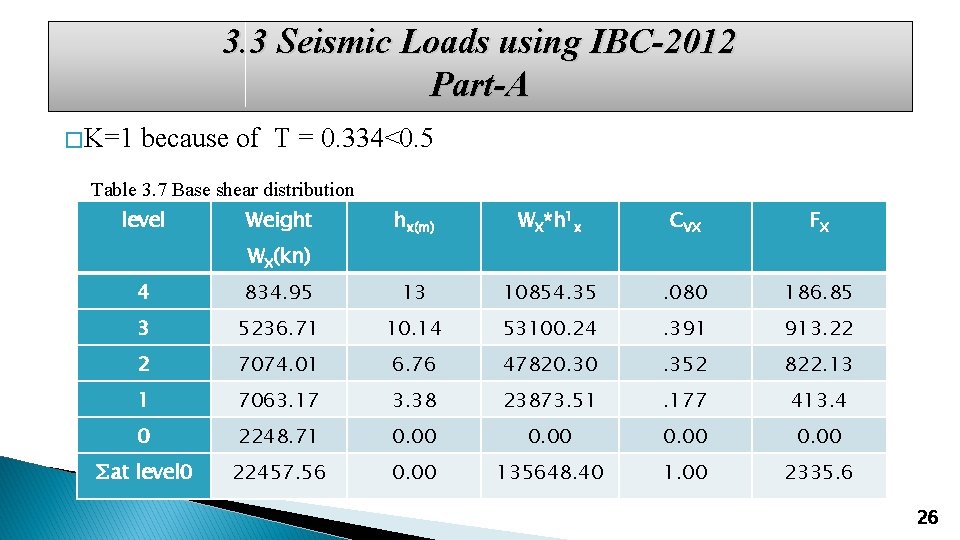
3. 3 Seismic Loads using IBC-2012 Part-A � K=1 because of T = 0. 334<0. 5 Table 3. 7 Base shear distribution level Weight hx(m) WX*h 1 x CVX FX WX(kn) 4 834. 95 13 10854. 35 . 080 186. 85 3 5236. 71 10. 14 53100. 24 . 391 913. 22 2 7074. 01 6. 76 47820. 30 . 352 822. 13 1 7063. 17 3. 38 23873. 51 . 177 413. 4 0 2248. 71 0. 00 ∑at level 0 22457. 56 0. 00 135648. 40 1. 00 2335. 6 26

3. 4 Seismic Loads using IBC-2012 Part-B � The �V seismic base shear V: = C s. W �W = effective seismic weight= 12574. 55 KN � Ta = 0. 0488*8. 60. 75 = 0. 245 sec � The �V seismic base shear V = CSW = 0. 104*12574. 56 = 1307. 75 27

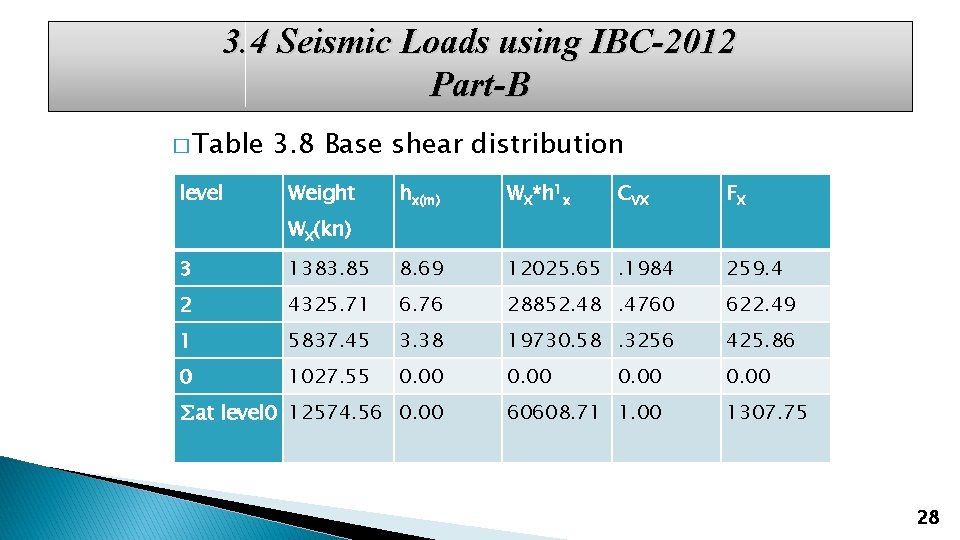
3. 4 Seismic Loads using IBC-2012 Part-B � Table level 3. 8 Base shear distribution Weight hx(m) WX*h 1 x CVX FX WX(kn) 3 1383. 85 8. 69 12025. 65. 1984 259. 4 2 4325. 71 6. 76 28852. 48. 4760 622. 49 1 5837. 45 3. 38 19730. 58. 3256 425. 86 0 1027. 55 0. 00 ∑at level 0 12574. 56 0. 00 60608. 71 1. 00 1307. 75 28

4. Structural Analysis Of Part A Using SAP 2000 UBC-97 � Equivalent � Ritz static and response spectrum analyses were used vectors mode is used to get modal mass participation ratio more than 90% Table 4. 1 Base shear comparison Equivalent static using hand calculations Equivalent static using sap 2000 Response spectrum X-direction Response spectrum Y-direction 2552 2546. 7 1933 1796 29

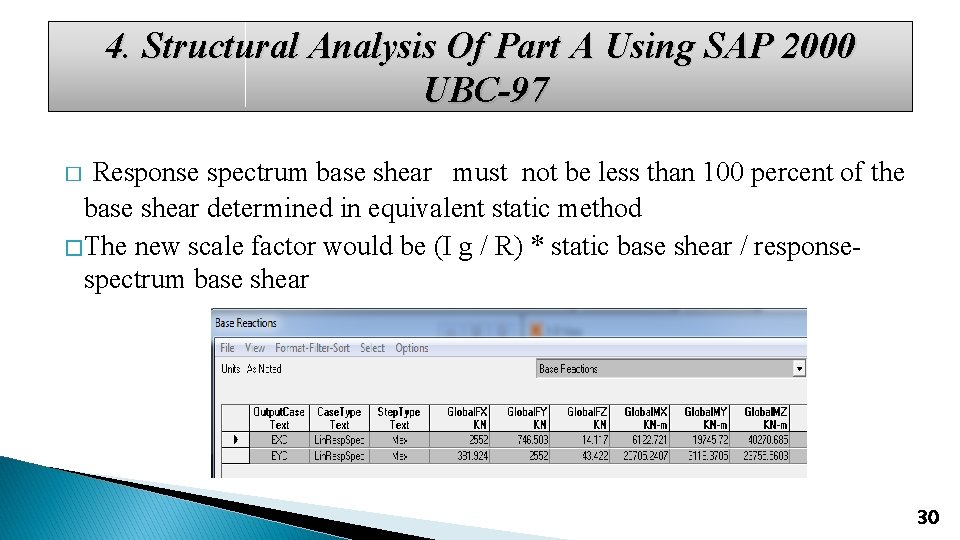
4. Structural Analysis Of Part A Using SAP 2000 UBC-97 Response spectrum base shear must not be less than 100 percent of the base shear determined in equivalent static method � The new scale factor would be (I g / R) * static base shear / responsespectrum base shear � 30

4. Structural Analysis Of Part A Using SAP 2000 IBC-2012 Table 4. 2 Base shear comparison Equivalent static using hand calculations Response spectrum X-direction Response spectrum Y-direction 2334. 6 2334. 47 1763. 7 1618. 9 • Response spectrum base shear has to be more than 85 percent of the base shear determined in equivalent static method 31

4. Structural Analysis Of Part A Using SAP 2000 IBC-2012 • The new scale factor would be 0. 85* (I g / R) * static base shear / response-spectrum base shear Table 4. 3 Dynamic base shear after modification EXD EYD 1984. 7 1980 32

4. Verification of Structural Analysis for Part A model � Compatibility � The structure and its joints are moving in one unit 33

4. Verification of Structural Analysis for Part A model Period (T) checked From sap � Modal x analysis (T) = (0. 123) � Modal y analysis (T) = (0. 096) � Reylof method (Tx =0. 13) � Reylof method (Ty = 0. 0988) 34

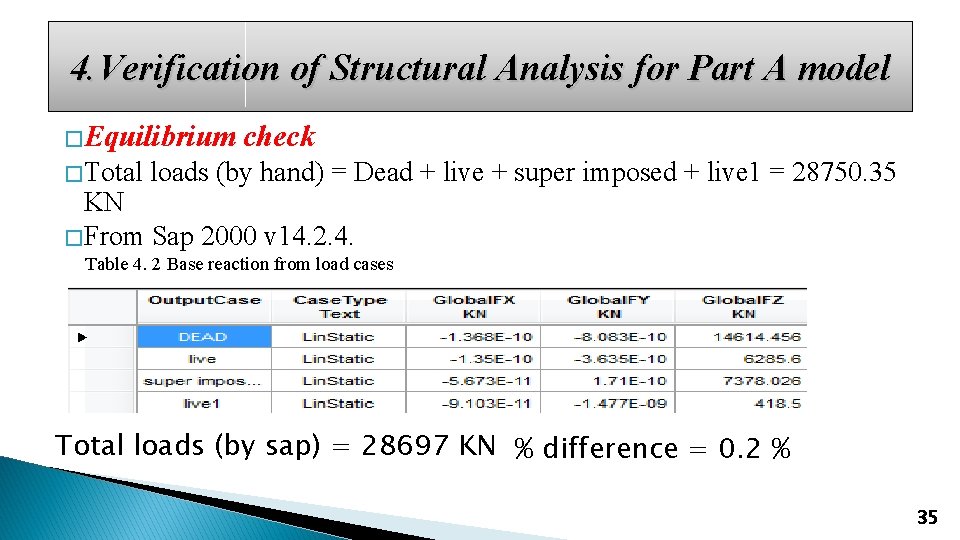
4. Verification of Structural Analysis for Part A model �Equilibrium � Total check loads (by hand) = Dead + live + super imposed + live 1 = 28750. 35 KN � From Sap 2000 v 14. 2. 4. Table 4. 2 Base reaction from load cases Total loads (by sap) = 28697 KN % difference = 0. 2 % 35

� 5. Wind And Snow Loads (General UBC 97) 36

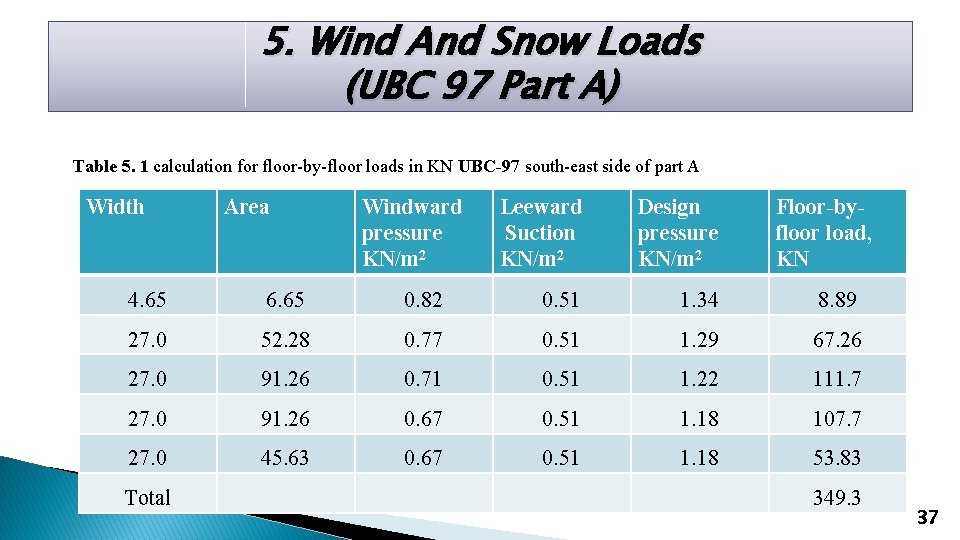
5. Wind And Snow Loads (UBC 97 Part A) Table 5. 1 calculation for floor-by-floor loads in KN UBC-97 south-east side of part A Width Area Windward pressure KN/m 2 Leeward Suction KN/m 2 Design pressure KN/m 2 Floor-byfloor load, KN 4. 65 6. 65 0. 82 0. 51 1. 34 8. 89 27. 0 52. 28 0. 77 0. 51 1. 29 67. 26 27. 0 91. 26 0. 71 0. 51 1. 22 111. 7 27. 0 91. 26 0. 67 0. 51 1. 18 107. 7 27. 0 45. 63 0. 67 0. 51 1. 18 53. 83 Total 349. 3 37

5. Wind And Snow Loads (General ASCE 7 -10 ) ASCE 7 -10 Analysis Design Wind Pressure � Category of building is C � Basic wind speed = 185 Km/hr � The velocity pressure, qz = 0. 613 Kz Kd Kzt V 2 (N/m 2) Where: � Kz = velocity pressure exposure coefficient at any height � Kh = velocity pressure exposure coefficient at mean roof hieght 38

� Kd = 5. Wind And Snow Loads (General ASCE 7 -10 ) Wind Directionality factor = 0. 85 � Kzt = Topographic factor = 1. 0 � Cp = external pressure coefficient � G = gust factor = 0. 85 � V in m/sec = 185 Km/hr = 51. 39 m/sec 39

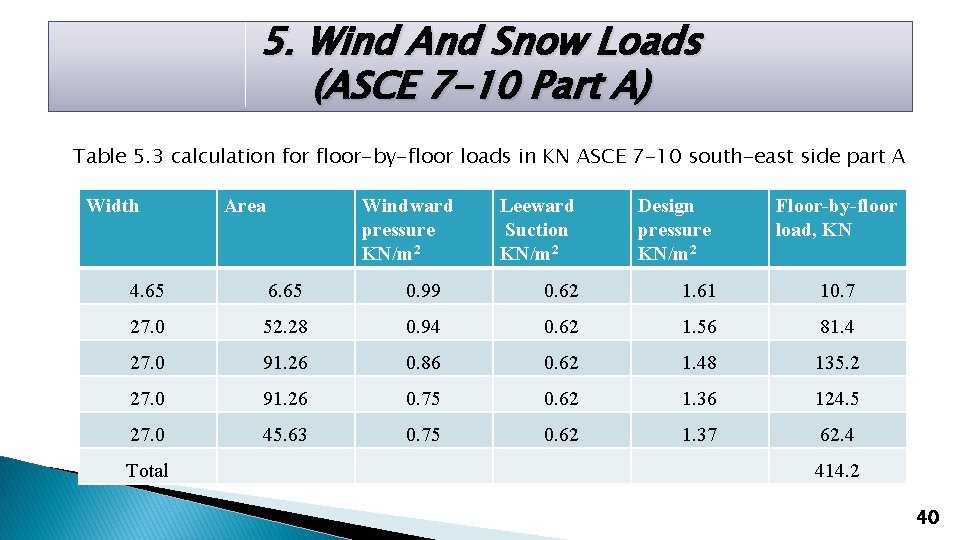
5. Wind And Snow Loads (ASCE 7 -10 Part A) Table 5. 3 calculation for floor-by-floor loads in KN ASCE 7 -10 south-east side part A Width Area Windward pressure KN/m 2 Leeward Suction KN/m 2 Design pressure KN/m 2 Floor-by-floor load, KN 4. 65 6. 65 0. 99 0. 62 1. 61 10. 7 27. 0 52. 28 0. 94 0. 62 1. 56 81. 4 27. 0 91. 26 0. 86 0. 62 1. 48 135. 2 27. 0 91. 26 0. 75 0. 62 1. 36 124. 5 27. 0 45. 63 0. 75 0. 62 1. 37 62. 4 Total 414. 2 40

5. Wind And Snow Loads � Jordanian code 2006 � Site snow load (S 0): Snow load at site land level in KN/m 2 � H = 230 m Table 5. 5 Snow load at site level � S 0= 0 KN/m 2 S 0(KN/m 2) Height of construction site above sea level in meters. 0 250 > h (h-250)/800 500 > h > 250 (h-400)/320 1500 > h > 500 41

6. Final design (slabs) Figure 6. 1 Area Of Steel From SAP Figure 6. 2 Positive Envelope Ultimate Moment 42

6. Final design (slabs) �From hand calculations As = 165 mm 2, %difference = 7. 8% �As min = 0. 0018 * b * h = 270 mm 2 �Use 4φ10 mm/m �Check for shear, Vu is less than φVc Vu=22. 7 KN from sap φVc=72. 8 KN No need for stirrups 43

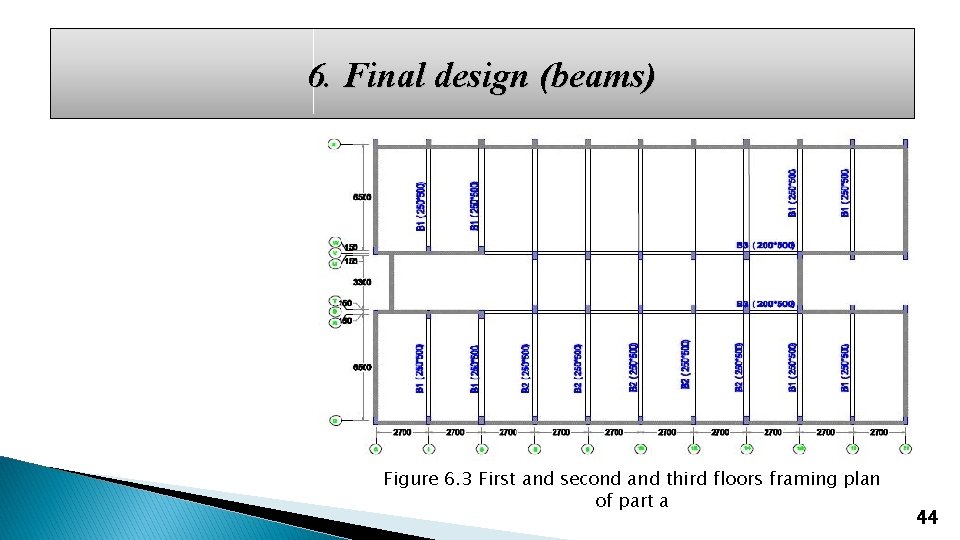
6. Final design (beams) Figure 6. 3 First and second and third floors framing plan of part a 44

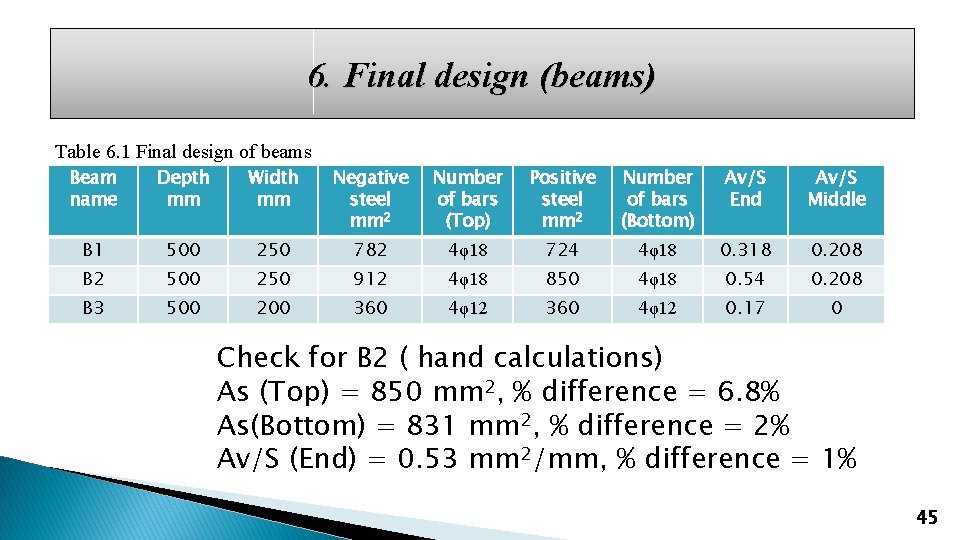
6. Final design (beams) Table 6. 1 Final design of beams Beam name Depth mm Width mm Negative steel mm 2 Number of bars (Top) Positive steel mm 2 Number of bars (Bottom) Av/S End Av/S Middle B 1 500 250 782 4φ18 724 4φ18 0. 318 0. 208 B 2 500 250 912 4φ18 850 4φ18 0. 54 0. 208 B 3 500 200 360 4φ12 0. 17 0 Check for B 2 ( hand calculations) As (Top) = 850 mm 2, % difference = 6. 8% As(Bottom) = 831 mm 2, % difference = 2% Av/S (End) = 0. 53 mm 2/mm, % difference = 1% 45

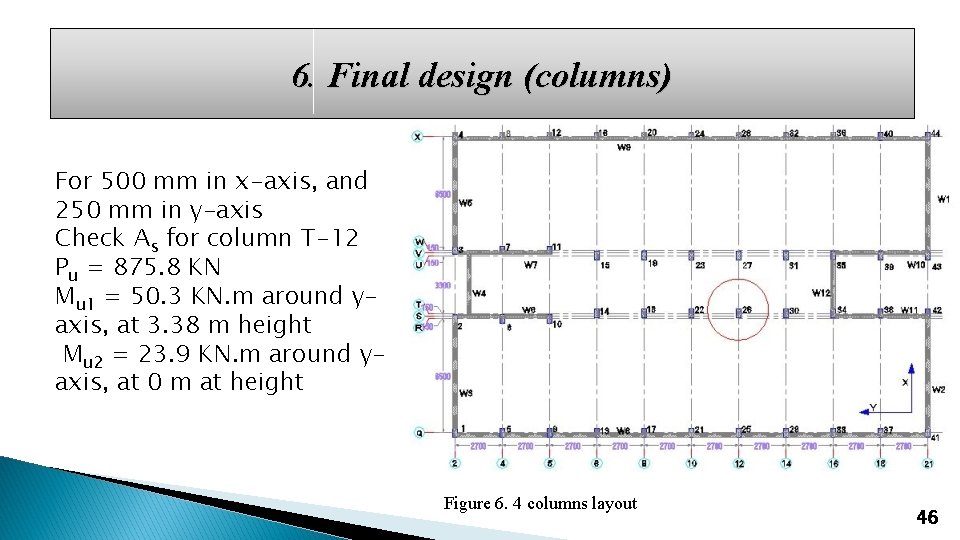
6. Final design (columns) For 500 mm in x-axis, and 250 mm in y-axis Check As for column T-12 Pu = 875. 8 KN Mu 1 = 50. 3 KN. m around yaxis, at 3. 38 m height Mu 2 = 23. 9 KN. m around yaxis, at 0 m at height Figure 6. 4 columns layout 46

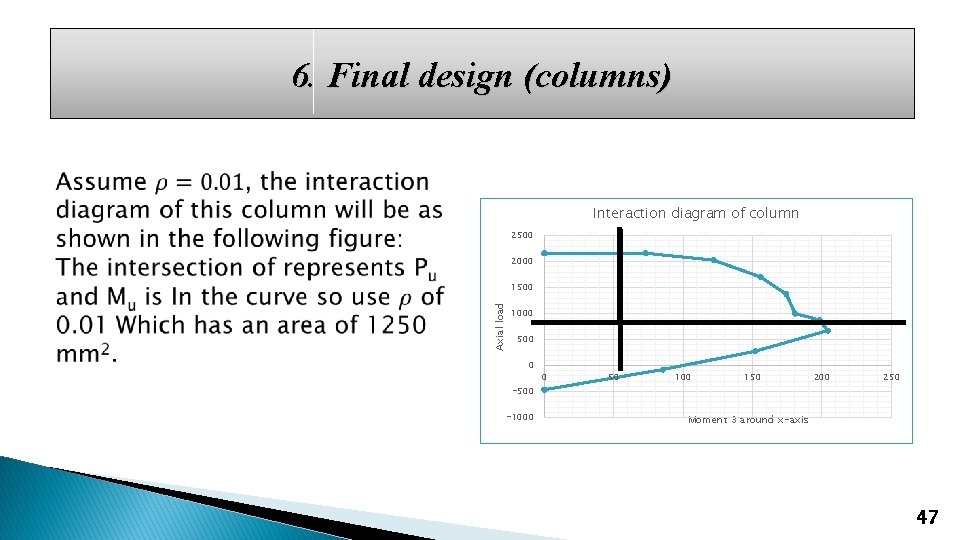
6. Final design (columns) Interaction diagram of column 2500 2000 Axial load 1500 1000 500 0 -500 -1000 0 50 100 150 200 250 Moment 3 around x-axis 47

6. Final design (columns) Spacing so shall not exceed the smallest of the following: - 8*db = 8*16 = 128 mm - 24 dt = 24*10 = 240 mm - ½ of smallest dimension = 125 mm - 300 mm - Use so = 100 mm The first hoop shall be located at not more than 50 mm from the joint face. 48

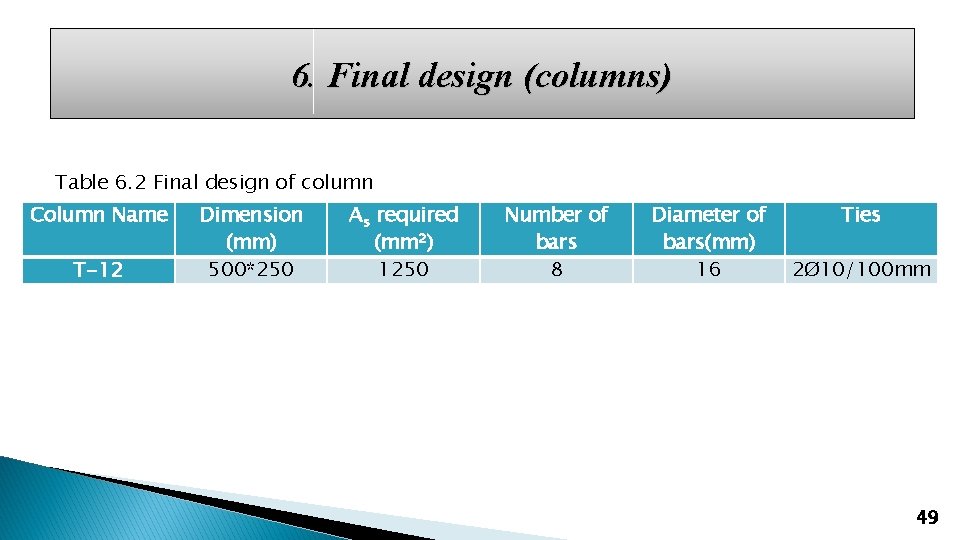
6. Final design (columns) Table 6. 2 Final design of column Column Name T-12 Dimension (mm) 500*250 As required (mm 2) 1250 Number of bars 8 Diameter of bars(mm) 16 Ties 2Ø 10/100 mm 49

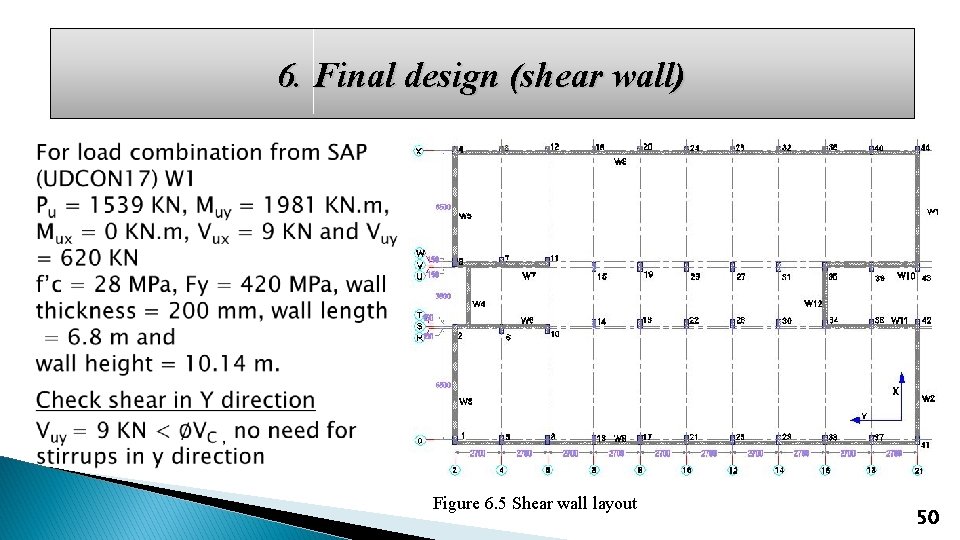
6. Final design (shear wall) Figure 6. 5 Shear wall layout 50

6. Final design (shear wall) 51

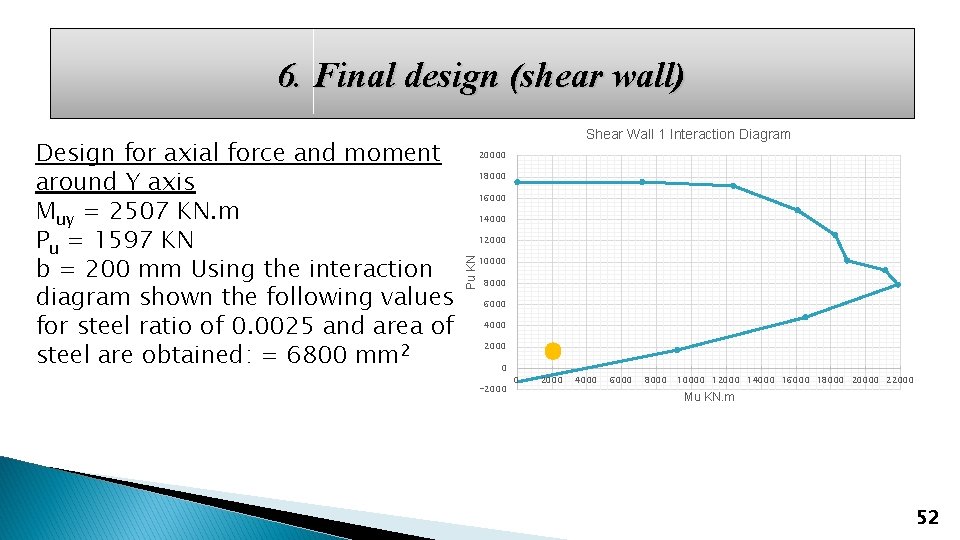
6. Final design (shear wall) 20000 18000 16000 14000 12000 Pu KN Design for axial force and moment around Y axis Muy = 2507 KN. m Pu = 1597 KN b = 200 mm Using the interaction diagram shown the following values for steel ratio of 0. 0025 and area of steel are obtained: = 6800 mm 2 Shear Wall 1 Interaction Diagram 10000 8000 6000 4000 2000 0 -2000 0 2000 4000 6000 8000 10000 12000 14000 16000 18000 20000 22000 Mu KN. m 52

6. Final design (shear wall) ρmin = 0. 0025 As = 0. 0025 × 200 × 6800 = 3400 mm 2 Use 2 Ø 10 mm @ 250 mm For opening in the walls the same area of steel distribution are used 53

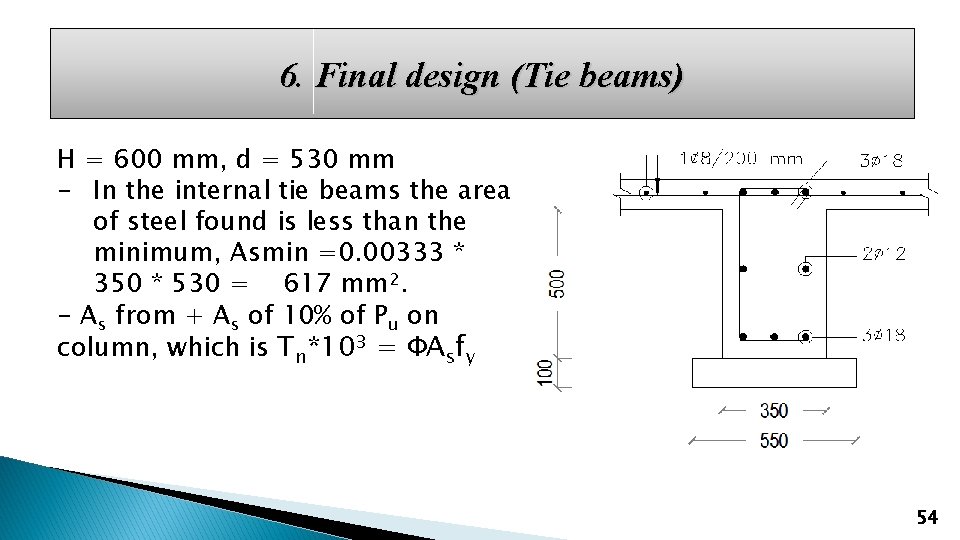
6. Final design (Tie beams) H = 600 mm, d = 530 mm - In the internal tie beams the area of steel found is less than the minimum, Asmin =0. 00333 * 350 * 530 = 617 mm 2. - As from + As of 10% of Pu on column, which is Tn*103 = ФAsfy 54

6. Final design (diaphragm) � Diaphragm is a horizontal system acting to transmit lateral forces to vertical-resisting elements (slab system). � Types of diaphragms: a) Rigid diaphragm b) Flexible diaphragm 55

6. 1 Final design (diaphragm) � The diaphragm design force � Fpx = the diaphragm design force � Fi = the design force applied to Level I � wi = the weight tributary to Level i � wpx = the weight tributary to the diaphragm at Level x 56

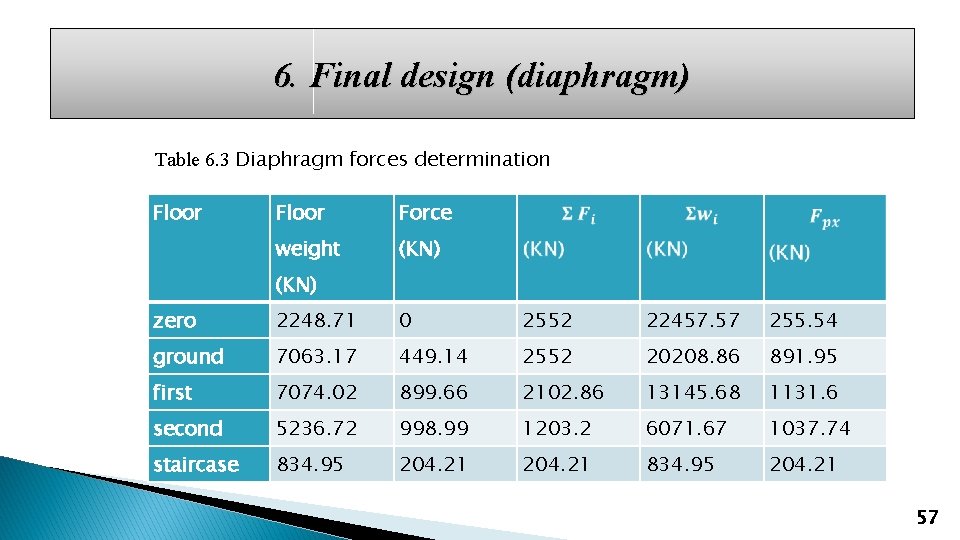
6. Final design (diaphragm) Table 6. 3 Diaphragm forces determination Floor Force weight (KN) zero 2248. 71 0 2552 22457. 57 255. 54 ground 7063. 17 449. 14 2552 20208. 86 891. 95 first 7074. 02 899. 66 2102. 86 13145. 68 1131. 6 second 5236. 72 998. 99 1203. 2 6071. 67 1037. 74 staircase 834. 95 204. 21 57

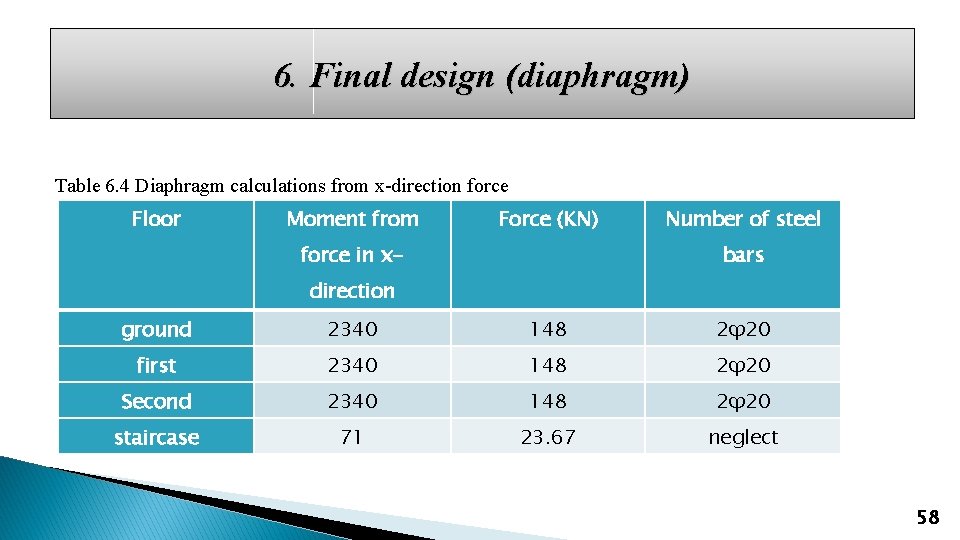
6. Final design (diaphragm) Table 6. 4 Diaphragm calculations from x-direction force Floor Moment from Force (KN) force in x- Number of steel bars direction ground 2340 148 2ϕ 20 first 2340 148 2ϕ 20 Second 2340 148 2ϕ 20 staircase 71 23. 67 neglect 58

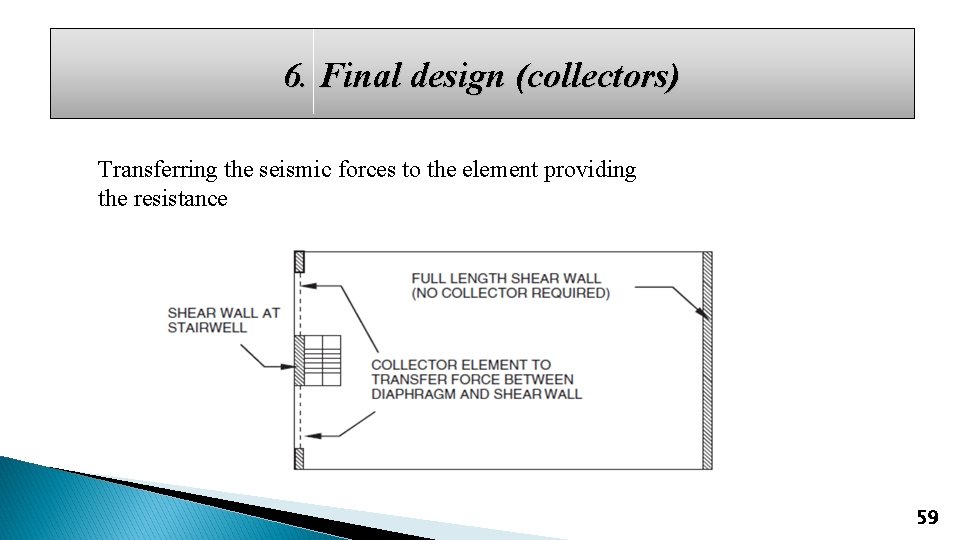
6. Final design (collectors) Transferring the seismic forces to the element providing the resistance 59

6. Final design (horizontal structural irregularity) � A. B. Torsional Irregularity Extreme Torsional Irregularity The torsional irregularity is not exited The extreme torsional irregularity is not exited 60

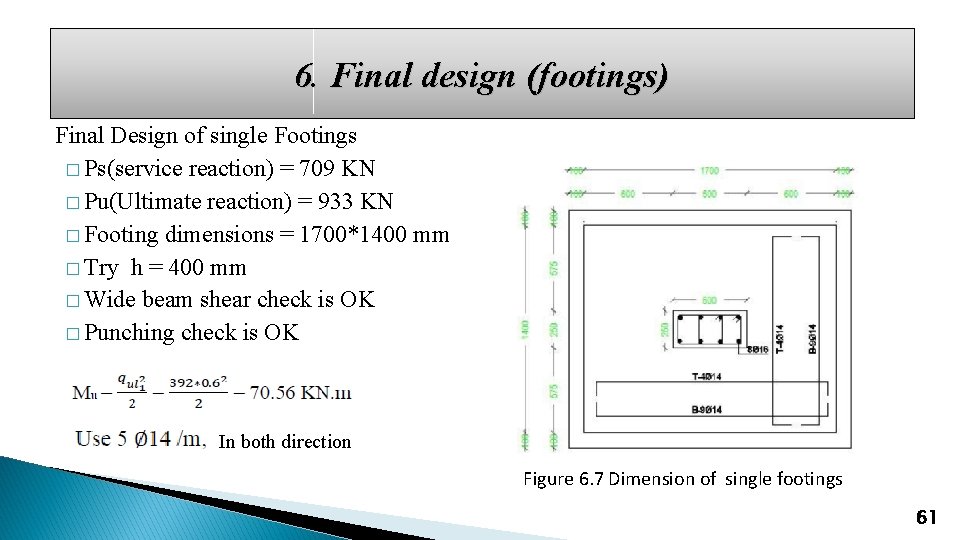
6. Final design (footings) Final Design of single Footings � Ps(service reaction) = 709 KN � Pu(Ultimate reaction) = 933 KN � Footing dimensions = 1700*1400 mm � Try h = 400 mm � Wide beam shear check is OK � Punching check is OK In both direction Figure 6. 7 Dimension of single footings 61

6. Final design (wall footings) � Service reaction (Ps) = 1229 KN, service moment(Ms) = 1407 KN. m � Ultimate reaction (Pu) = 1571 KN, Ultimate moment (Mu) = 2555 KN. m � B = �������� /���� = 1229/7. 3330 = 0. 5 m use B= 1 m � Try h=350 mm � Wide beam shear and punching is OK 62

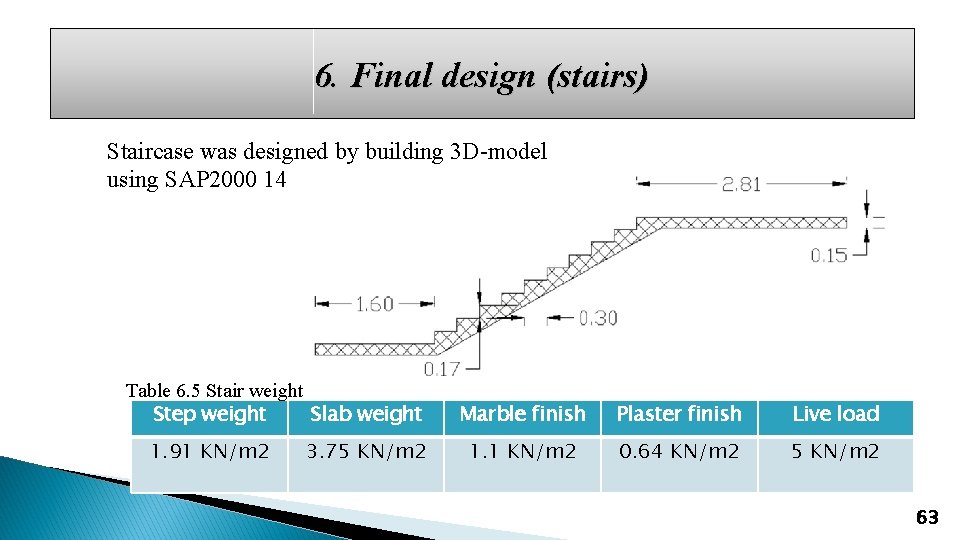
6. Final design (stairs) Staircase was designed by building 3 D-model using SAP 2000 14 Table 6. 5 Stair weight Step weight Slab weight 1. 91 KN/m 2 3. 75 KN/m 2 Marble finish Plaster finish Live load 1. 1 KN/m 2 0. 64 KN/m 2 5 KN/m 2 63

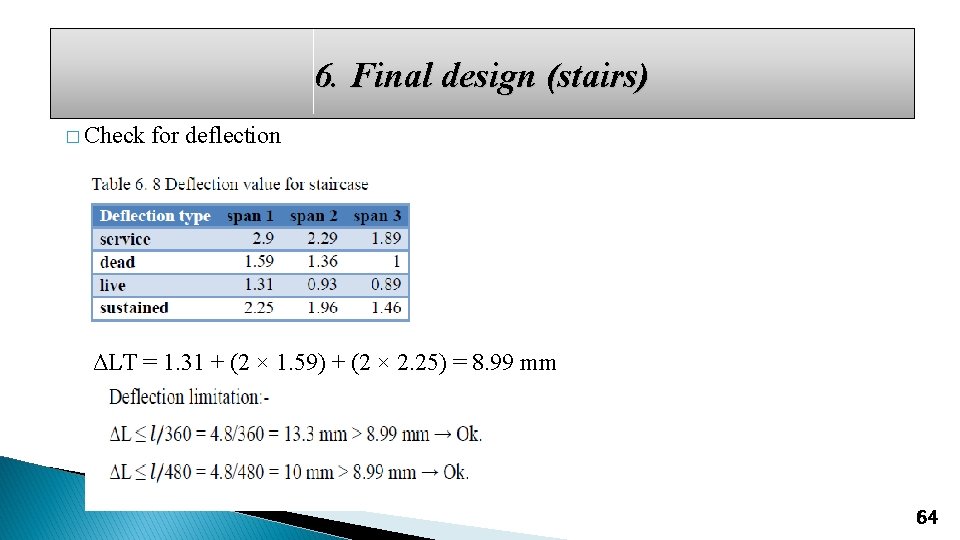
6. Final design (stairs) � Check for deflection ΔLT = 1. 31 + (2 × 1. 59) + (2 × 2. 25) = 8. 99 mm 64

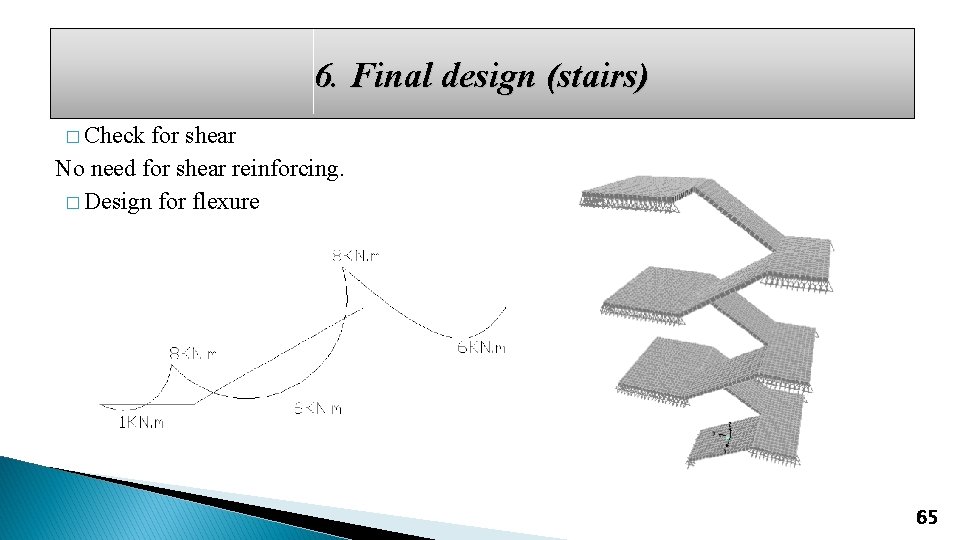
6. Final design (stairs) � Check for shear No need for shear reinforcing. � Design for flexure 65

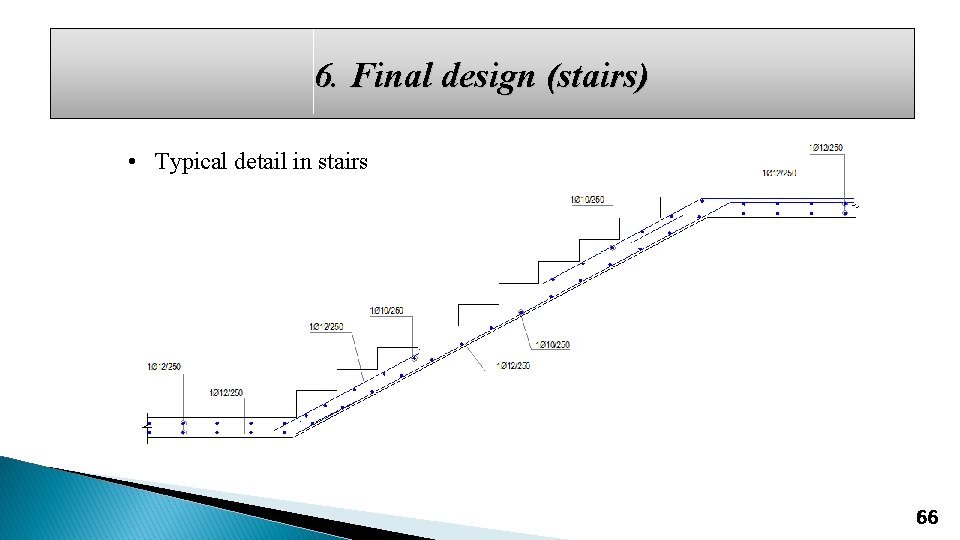
6. Final design (stairs) • Typical detail in stairs 66

6. Seismic Demands on Non-Structural Components � Internal partition analysis and design � Fp = seismic design force Fp=5. 7 KN Mu=2. 4 KN. m As = 65 mm 2 As min = 360 mm 2 Use 5 ∅ 10 at 1 m 67

68