Structura i organizarea calculatoarelor curs 2009 Ionescu AugustinIulian

Structura şi organizarea calculatoarelor - curs 2009 Ionescu Augustin-Iulian

Capitolul 1 ARITMETICA CALCULATOARELOR 2009 1. 2

Reprezentarea numerelor cu semn Prezentare generală Fie N un număr binar cu semn N=±bn-1 bn-2…b 1 b 0, b-1…b-m Deoarece într-un SN cu un număr par de cifre nu putem reprezenta direct numerele negative, se utilizează reprezentarea codificată. Codificarea semnului Codificarea valorii. • Cod direct (reprezentare prin mărime şi semn) • Cod complementar • Cod invers 2009 1. 3

Reprezentarea numerelor cu semn Reprezentarea virgulă fixă prin mărime şi semn Bitul de semn bs nu are pondere deci poate ocupa orice poziţie. Pentru evitarea confuziilor, bs este plasat întotdeauna în poziţia extremă stângă (bitul cel mai semnificativ). Valoarea numărului se reprezintă, indiferent de semn, prin modulul numărului. În concluzie, numărul va fi reprezentat sub forma: N=bsbn-1 bn-2…b 1 b 0 b-1…b-m În multe situaţii se consideră un caz particular al reprezentării şi anumerele sunt fracţionare. În acest caz bitul de semn apare ca prima cifră de la partea întreagă (b 0). N=bsb-1…b-m 2009 1. 4

Reprezentarea numerelor cu semn Exemple: Fie numarul N=+0, 74 reprezentat in format VF 1+15 prin marime si semn. Fie numarul N=-0, 74 reprezentat in format VF 1+15 prin marime si semn. 2009 1. 5

Reprezentarea numerelor cu semn Complementul faţă de 2 Fie N un număr binar reprezentat pe n ranguri întregi şi m ranguri fracţionare: N=bn-12 n-1+bn-22 n-2+…+b 121+b 0+b-12 -1+…. b-m 2 m-1 = = Se numeşte complement faţă de 2 al numărului N numărul calculat cu relaţia =2 n-N şi reprezentat în acelaşi format ca şi numărul N. 2009 1. 6

Reprezentarea numerelor cu semn Proprietate Fie numarul real N= . Atunci Complementul fata de 1 al lui N 2009 1. 7

Reprezentarea numerelor cu semn Reprezentare virgulă fixă în cod complementar 2009 1. 8

Reprezentarea numerelor cu semn Observații! 2009 1. 9

Reprezentarea numerelor cu semn Exemple Fie numarul N=+0, 74 reprezentat ȋn format VF 1+15 cod complementar. Fie numarul N=-0, 74 reprezentat ȋn format VF 1+15 cod complementar. 2009 1. 10

Deplasarea numerelor cu semn Deplasarea spre stânga este echivalentă cu înmulţirea cu 2. Cifra din extrema stângă se pierde iar prin dreapta se introduce 0, indiferent de modul de reprezentare a numerelor. Deplasarea spre dreapta este echivalentă cu împărţirea la 2 (înmulţirea cu 2 -1). Cifra din extrema dreaptă se pierde, iar prin stânga se introduce 0 în cazul numerelor reprezentate prin mărime şi semn sau bitul de semn în cazul numerelor reprezentate în cod complementar. Observație! Deplasarea numerelor cu semn afectează numai modulul numerelor, nu şi bitul de semn. 2009 1. 11

Deplasarea numerelor cu semn Exemple: 2009 1. 12

Deplasarea numerelor cu semn Exemple 2009 1. 13

Adunarea în cod complementar 2009 1. 14

Adunarea în cod complementar 2009 1. 15

Adunarea în cod complementar 2009 1. 16

Adunarea în cod complementar 2009 1. 17

Adunarea în cod complementar 2009 1. 18

Adunarea în cod complementar Concluzii! 2009 1. 19

Adunarea în cod complementar Exemple (1) 2009 1. 20

Adunarea în cod complementar Exemple (2) 2009 1. 21

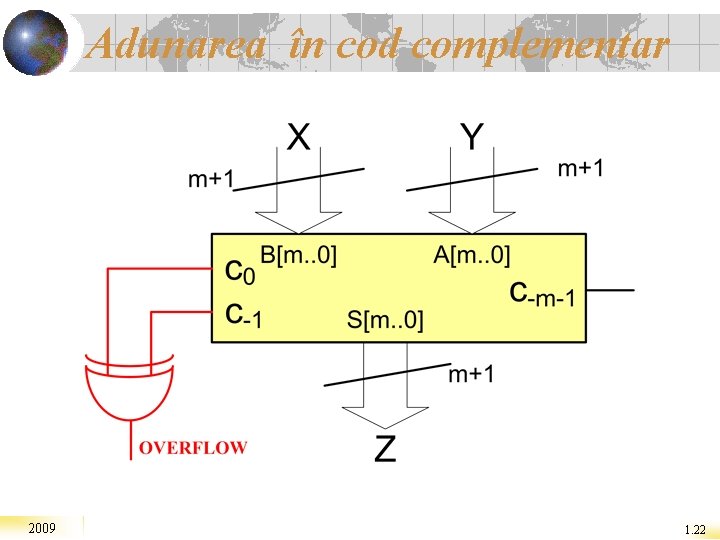
Adunarea în cod complementar 2009 1. 22

Scăderea în cod complementar 2009 1. 23

Scăderea în cod complementar 2009 1. 24

Scăderea în cod complementar 2009 1. 25

Scăderea în cod complementar 2009 1. 26

Scăderea în cod complementar 2009 1. 27

Scăderea în cod complementar Concluzii! 2009 1. 28

Scăderea în cod complementar Exemple: 2009 1. 29

Scăderea în cod complementar Exemple: 2009 1. 30

Scăderea în cod complementar Exemple: 2009 1. 31

Scăderea în cod complementar Exemple: 2009 1. 32

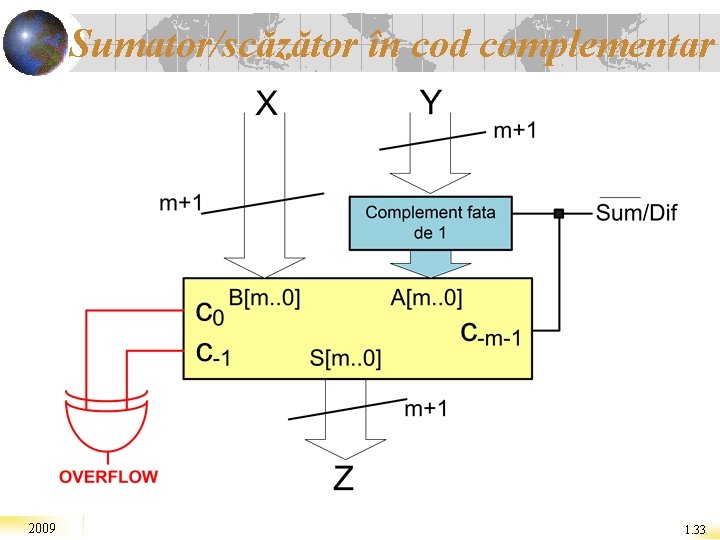
Sumator/scăzător în cod complementar 2009 1. 33

Adunarea în cod direct 2009 1. 34

Adunarea ȋn cod direct 2009 1. 35

Adunarea în cod direct 2009 1. 36

Adunarea în cod direct 2009 1. 37

Adunarea în cod direct v. Exemple: 2009 1. 38

Adunarea în cod direct v. Exemple: 2009 1. 39

Înmulţirea prin adunare-deplasare 11001 10101 -------11001 00000 11001 -------1000001101 2009 1. 40

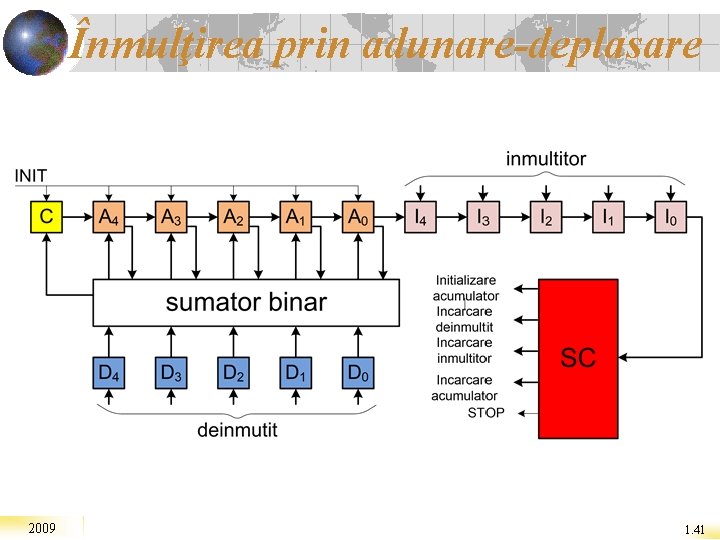
Înmulţirea prin adunare-deplasare 2009 1. 41

Înmulţirea prin adunare-deplasare 2009 1. 42

Metoda lui Booth Este utilizabilă pentru numere reprezentate în cod complementar. Algoritmul de calcul: Observatii! Bitul de referinţă pentru bitul cel mai puţin semnificativ este 0; După ultima comparare nu se mai realizează deplasarea. 2009 1. 43

Metoda lui Booth - exemplu Deȋnmulțitul X = 1, 0011 (-13/16) Înmulțitorul Y = 0, 1010 (+10/16) 00 deplasare dreapta 10 se scade X deplasare dreapta 01 se aduna X 2009 0, 0000 inițializare registru combinat 0, 0000 P 1 1, 0011 0, 11010000 P 2 0, 01101000 1, 0011 1, 10011000 P 3 1, 1100 1, 0011 0, 10011100 P 4 0, 01101000 1, 0011 1, 01111110 rezultat (-130/256) 1. 44

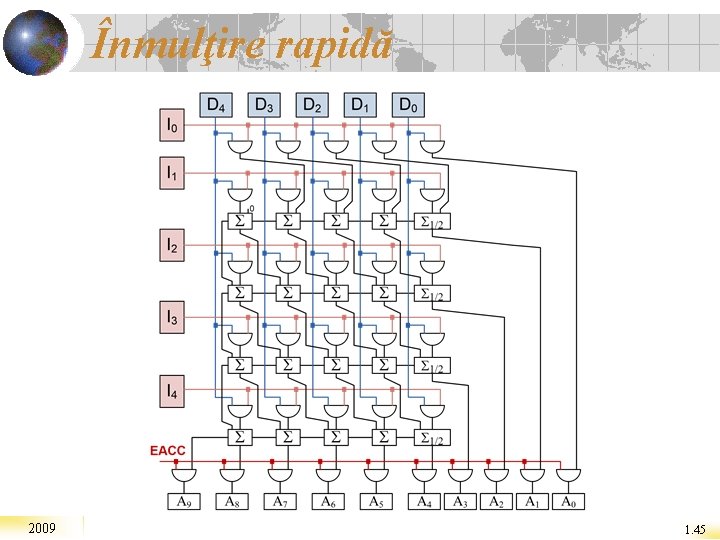
Înmulţire rapidă 2009 1. 45

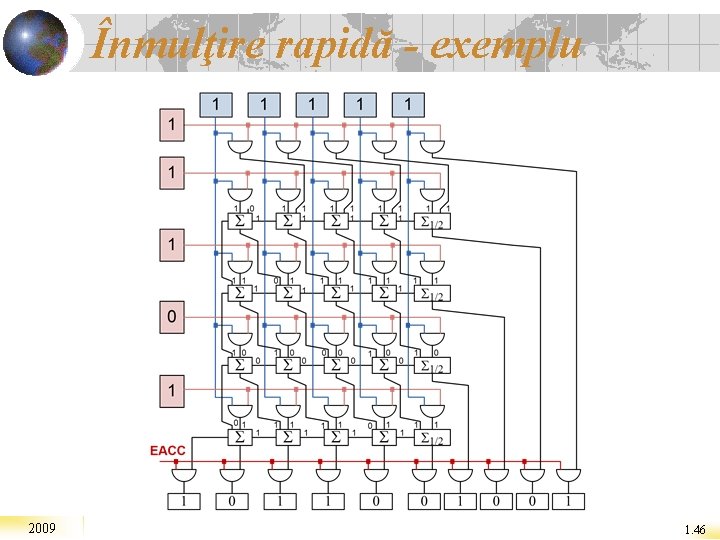
Înmulţire rapidă - exemplu 2009 1. 46

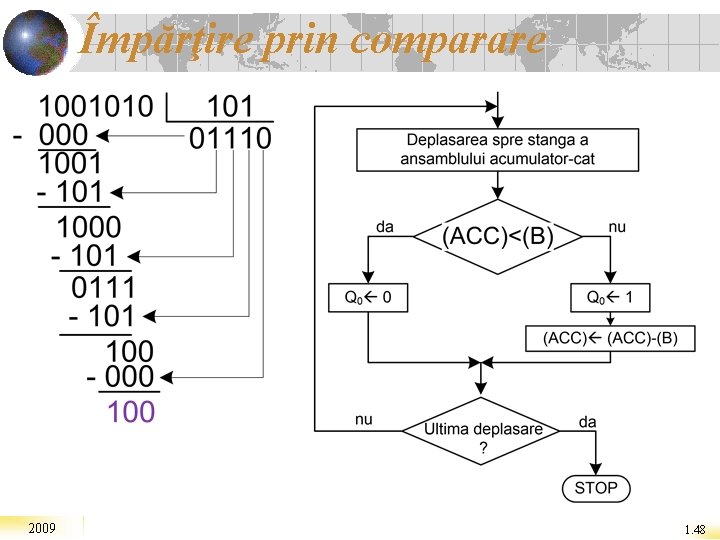
Împărţire prin comparare Există trei metode de împărţire în binar: Metoda comparării Metoda cu refacerea restului parţial Metoda fără refacerea restului parţial 2009 1. 47

Împărţire prin comparare 2009 1. 48

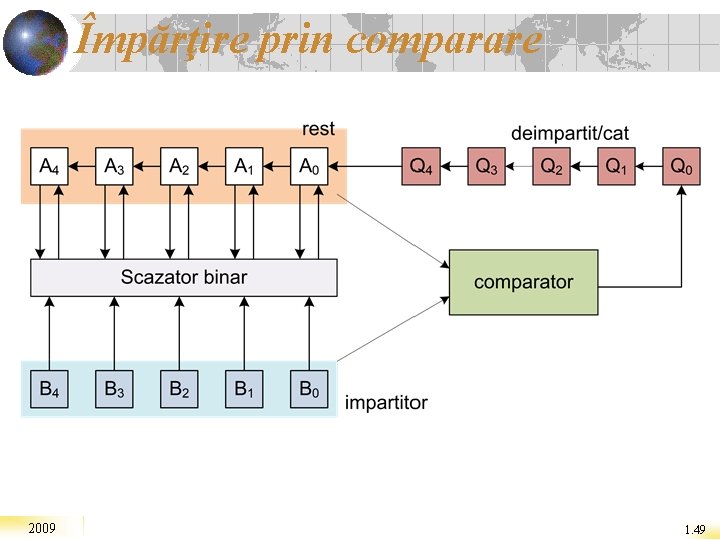
Împărţire prin comparare 2009 1. 49

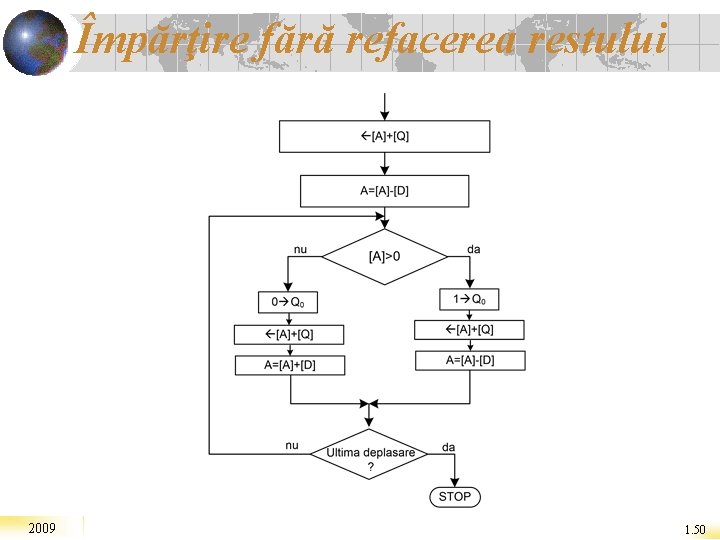
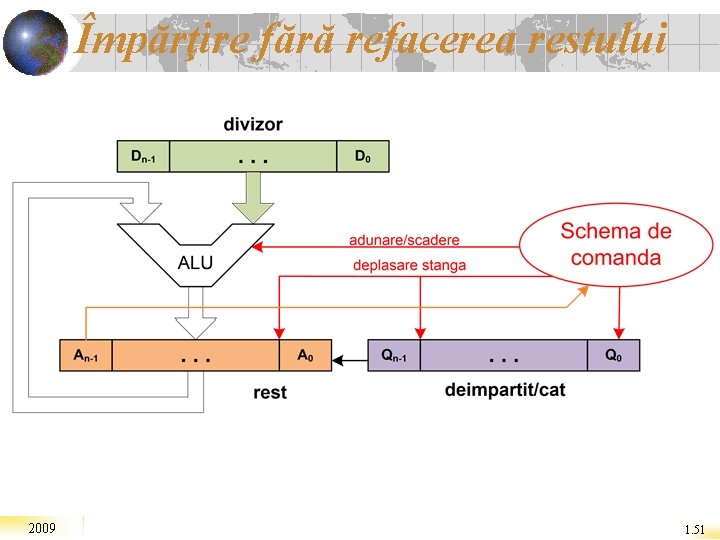
Împărţire fără refacerea restului 2009 1. 50

Împărţire fără refacerea restului 2009 1. 51

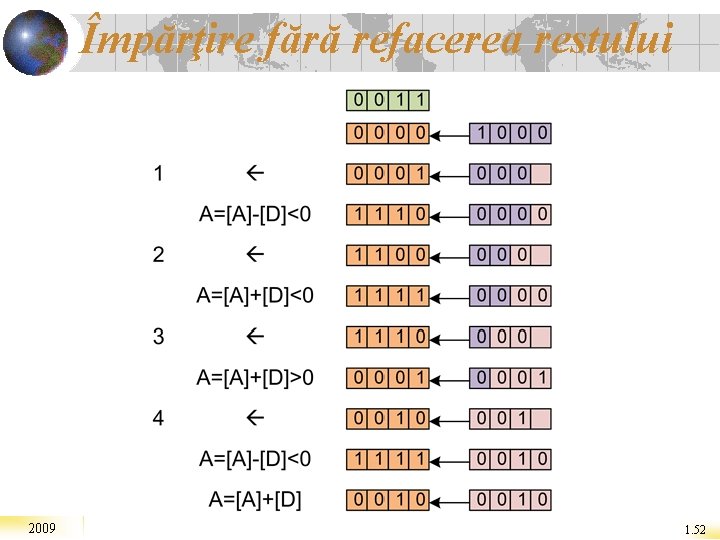
Împărţire fără refacerea restului 2009 1. 52