Strongly Correlated Electron Materials a Challenge for the

Strongly Correlated Electron Materials: a Challenge for the 21 st Century Gabriel Kotliar and Center for Materials Theory Colloquium Harvard University April 19 2010 $upport : NSF -DMR , DOE-Basic Energy Sciences, MURI, materials world network. 1

Outline • Introduction to the problem of strongly correlated electron systems • Introduction to some ideas and techniques from dynamical mean field theory (DMFT) • Application to the most correlated element Pu • Application to copper oxides. • Outlook Collaborators. Rutgers, K. Haule, C. Weber, J. Shim T. Stanescu, M. Civelli Paris, M. Ferrero, A. Georges, L. De. Leo, P. Cornaglia, O Parcollet Sherbrooke, A. M. Tremblay B. Kyung D. Senechal $upport : NSF -DMR , DOE-Basic Energy Sciences, MURI, NSF materials world network. 1

Standard Model of Solid State Physics • In many materials ( Cu, Au, …)electrons in solids behave as waves, quasiparticles [Sommerfeld Bloch] Metals conduct! • The Coulomb interactions renormalize to zero at low energies [ Landau] • Density functional theory in the LDA gives good estimates for the density and a good starting point for computing spectra [Kohn Sham ] • First order perturbation theory in the screened Coulomb interactions [GW ] is in good agreement with experiments. [Hedin] 2

Different approach is needed for magnetic insulators • In other materials Ni. O, Sm. Co 5 …Electron behave as particles • Solid as a collection of (open shell )atoms with localized electrons. • Interaction among the atom (exchange) order the atomic degrees of freedom (magnetic moments…. ) • Excitation spectra: multiplet theory, Hubbard bands, low wavelength collective fluctuations (spin waves) 3

Strongly Correlated Materials • Not well described by either the fully localized picture (well separated atoms) or the band picture (weakly interacting bloch waves). Materials for which the standard model of the solid state fails. Challenging non perturbative problem. • Continuous discovery of interesting material and phenomena that did not fit the standard model of solid state physics. Heavy fermions (early 80’s) , high temperature superconductors (late 80’s), other transition metal oxides (cobaltates, manganites, vanadates…. ) 90’s. . high Tc in Fe. As based compounds (2009). Interesting Correlated Materials discovered by serendipity and the Edisonian approach 4

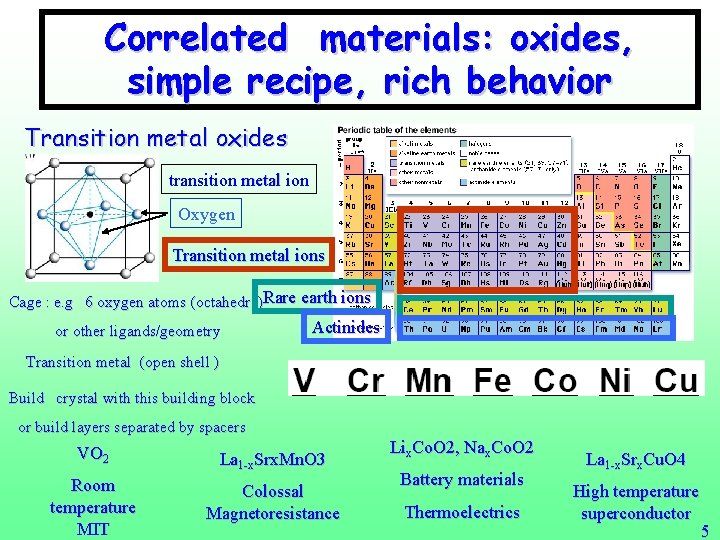
Correlated materials: oxides, simple recipe, rich behavior Transition metal oxides transition metal ion Oxygen Transition metal ions Cage : e. g 6 oxygen atoms (octahedra)Rare earth ions or other ligands/geometry Actinides Transition metal (open shell ) Build crystal with this building block or build layers separated by spacers VO 2 La 1 -x. Srx. Mn. O 3 Room temperature MIT Colossal Magnetoresistance Lix. Co. O 2, Nax. Co. O 2 Battery materials Thermoelectrics La 1 -x. Srx. Cu. O 4 High temperature superconductor 5

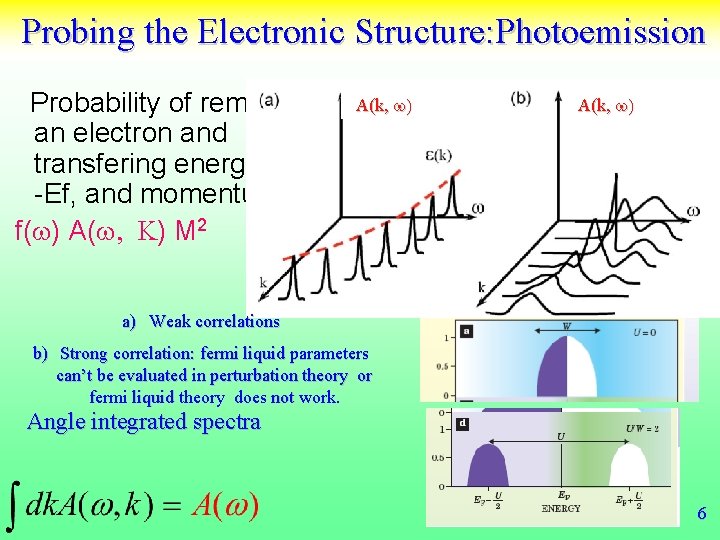
Probing the Electronic Structure: Photoemission Probability of removing an electron and transfering energy w=Ei -Ef, and momentum k f(w) A(w, K) M 2 e A(k, w) w a) Weak correlations b) Strong correlation: fermi liquid parameters can’t be evaluated in perturbation theory or fermi liquid theory does not work. Angle integrated spectra 6

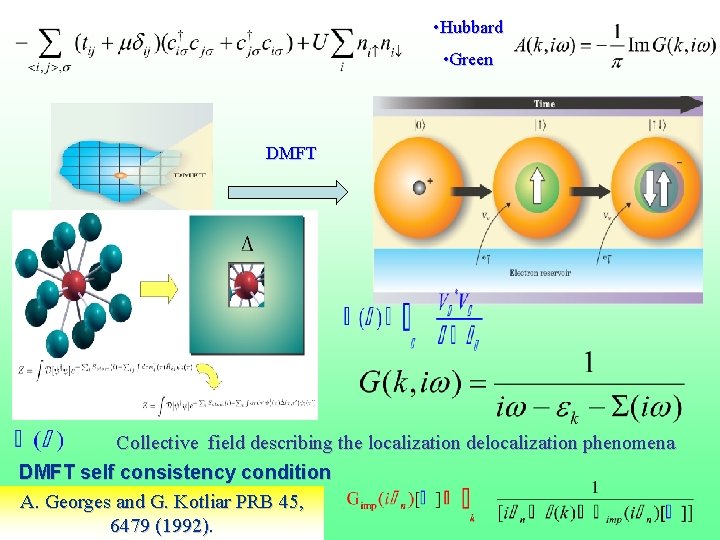
• Hubbard • Green DMFT Collective field describing the localization delocalization phenomena DMFT self consistency condition A. Georges and G. Kotliar PRB 45, 6479 (1992).

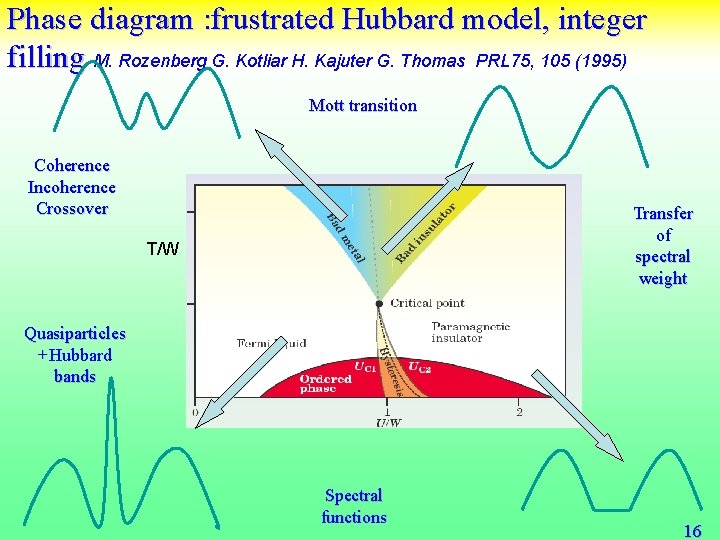
Phase diagram : frustrated Hubbard model, integer filling M. Rozenberg G. Kotliar H. Kajuter G. Thomas PRL 75, 105 (1995) Mott transition Coherence Incoherence Crossover Transfer of spectral weight T/W Quasiparticles +Hubbard bands Spectral functions 16

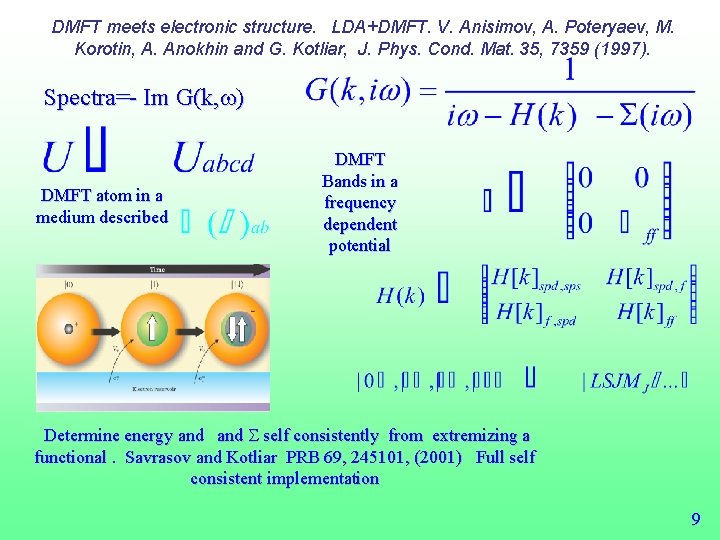
DMFT meets electronic structure. LDA+DMFT. V. Anisimov, A. Poteryaev, M. Korotin, A. Anokhin and G. Kotliar, J. Phys. Cond. Mat. 35, 7359 (1997). Spectra=- Im G(k, w) DMFT atom in a medium described DMFT Bands in a frequency dependent potential Determine energy and S self consistently from extremizing a functional. Savrasov and Kotliar PRB 69, 245101, (2001) Full self consistent implementation 9

Dynamical Mean Field Theory DMFT • Describes the electron both in the itinerant (wave-like) and localized (particle-like) regimes and everything in between!. • Simpler reference systems to understand correlated solids [e. g. harmonic oscillator] • Impurity model non gaussian reference frame (dressed atom). Tools to think about correlated materials. Weiss field quantifies the notion of itineracy. Configuration histograms generalizes CI. • CDMFT Reference state cluser of sites ( links, triangles, plaquettes, etc. ) • Locality assumption v accurate at high T (recent comparisons with cold atoms expts. and exact numerical techniques) Kozik et. al. ar. Xiv: 0907. 0863 Schneider et. al. Science, 322, 1520(2008). • Exact in the Metzner Vollhardt limit of infinite dimensions. 10

• Impurity solvers[ Recent advances, CTQMC Gull et. al. EPL 82, 57003 (2008), P. Werner et. al. Phys. Rev. Lett. 97, 076405 (2006) Bold CTQMC , OCA K. Haule ar. Xiv: 0907. 0195 Phys. Rev. B 75, 155113 (2007) …. . ] • Breaks problems in two parts a) study of mean field states from b ) evaluation of their energies. • Compare different “ mean field states” of the system for the same value of parameters. Understand “mechanism” for ordering. • Qualitative lessons can be drawn from (a) applied to simple models. High temperature universality. • Low temperature, multiple ordered states. Detailed comparison experiments requires realistic implementions of electronic structure, e. g. LDA+DMFT. • Bridge between atomic information and physical properties. (Structure-Property relation ). • Theoretical spectroscopy. 11

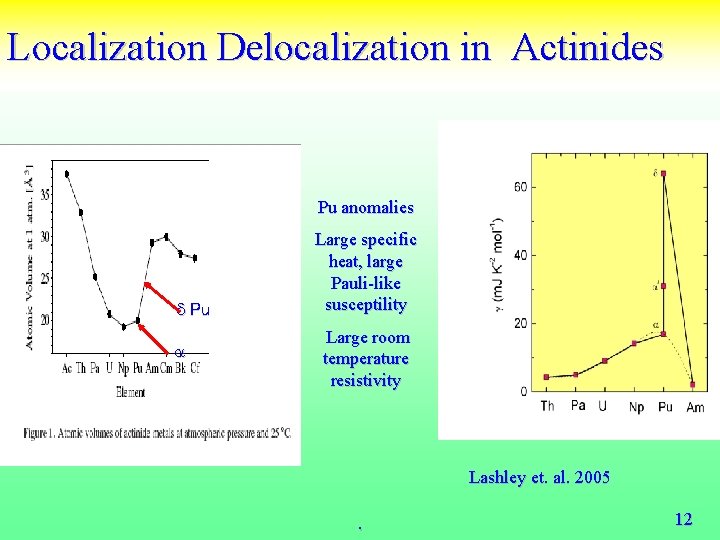
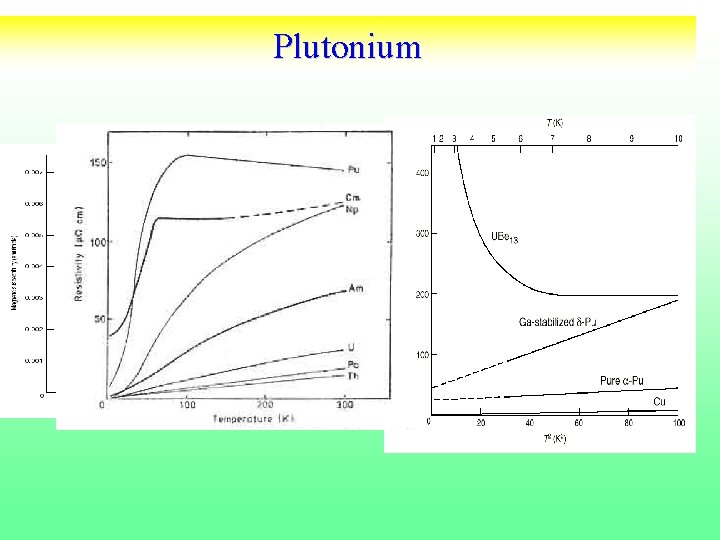
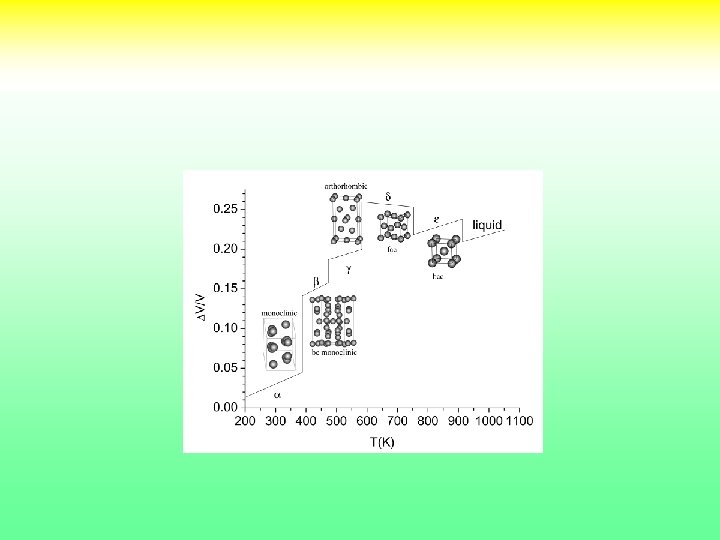
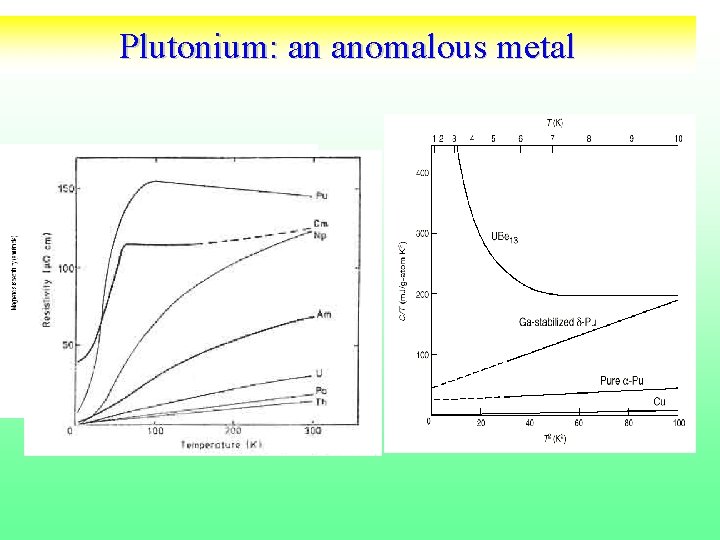
Localization Delocalization in Actinides Mott Transition d Pu a a Pu anomalies Large specific heat, large Pauli-like susceptility Large room temperature resistivity Lashley et. al. 2005 . 12

The standard model of solids fails near Pu • Spin Density functional theory predicts that Pu , Am are magnetic, large orbital and spin moments. • Experiments (Lashley et. al. 2005, Heffner et al. (2006)): d Pu is non magnetic. No static or fluctuating moments. Susceptibility, specific heat in a field, neutron quasielastic and inelastic scattering, muon spin resonance. • Paramagnetic LDA underestimates Volume of d Pu by 30% • Within LDA d Pu has unstable phonon modes. • Thermodynamic and transport properties similar to other strongly correlated materials. Pu strongly correlated paramagnetic metal 13

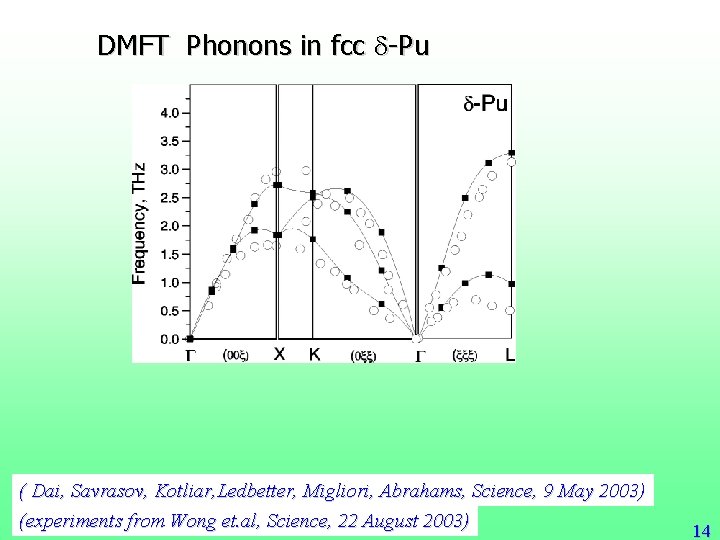
DMFT Phonons in fcc d-Pu ( Dai, Savrasov, Kotliar, Ledbetter, Migliori, Abrahams, Science, 9 May 2003) (experiments from Wong et. al, Science, 22 August 2003) 14

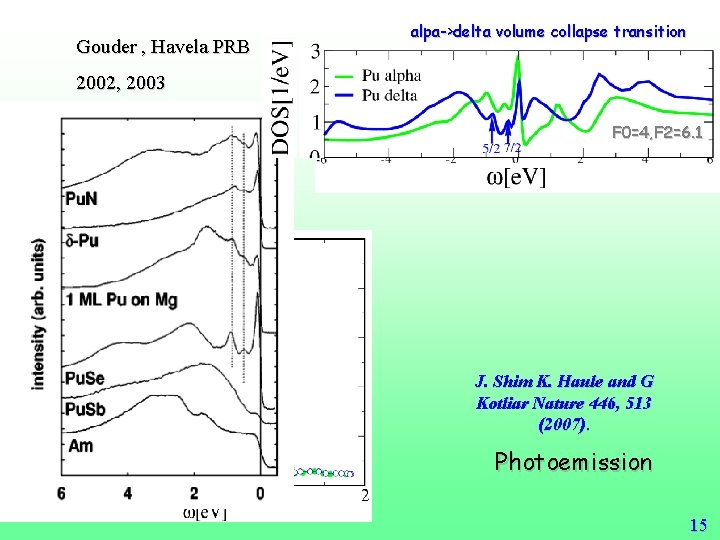
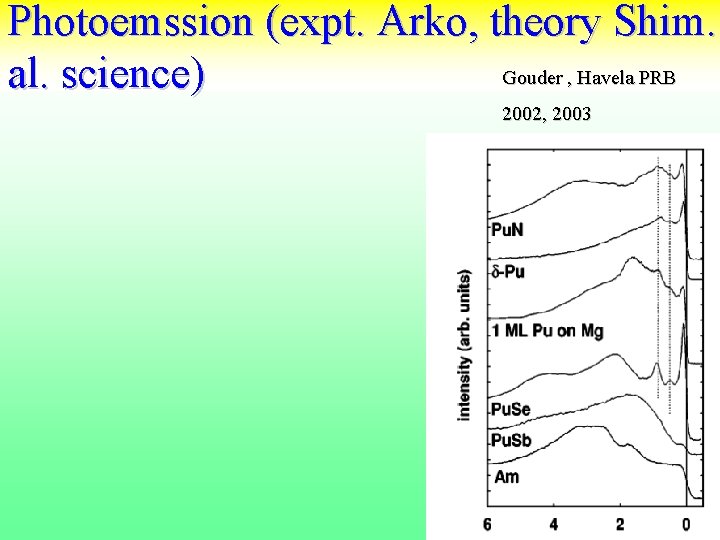
Gouder , Havela PRB alpa->delta volume collapse transition 2002, 2003 F 0=4, F 2=6. 1 J. Shim K. Haule and G Kotliar Nature 446, 513 (2007). Photoemission 15

Conclusions: elemental actinides. • Physical realization of the Mott localization-delocalization phenomena. • Successful testbed for the LDA+DMFT method, volume, phonon spectra. Plutonium is non magnetic Curium is magnetic with large moment. • Delta Pu, T* ~ 800 K, mixed valent 20 % f 6 80 % f 5 strong coupling to the lattice. • Moment screening by valence fluctuations. s • Reconciles susceptibility, XAS, and specific heat expts. • Quasiparticle multiplets, material specific fingerprints in the photoemisson spectra of Pu compounds. Prediction : temperature dependence. 16

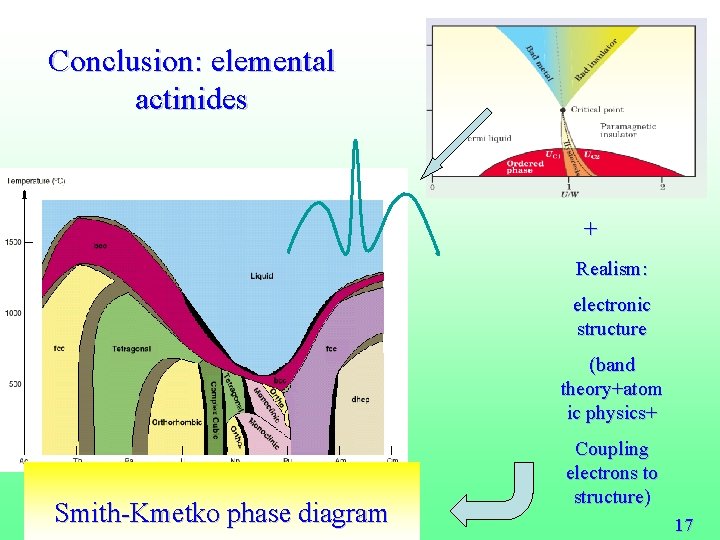
Conclusion: elemental actinides + Realism: electronic structure (band theory+atom ic physics+ Smith-Kmetko phase diagram Coupling electrons to structure) 17

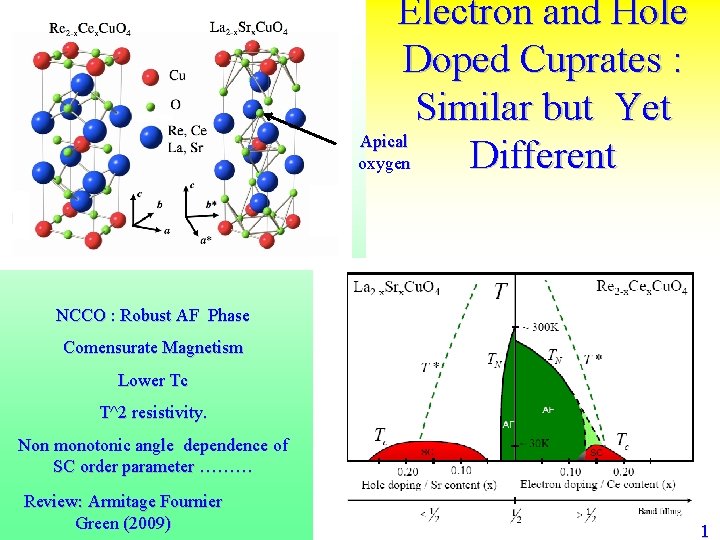
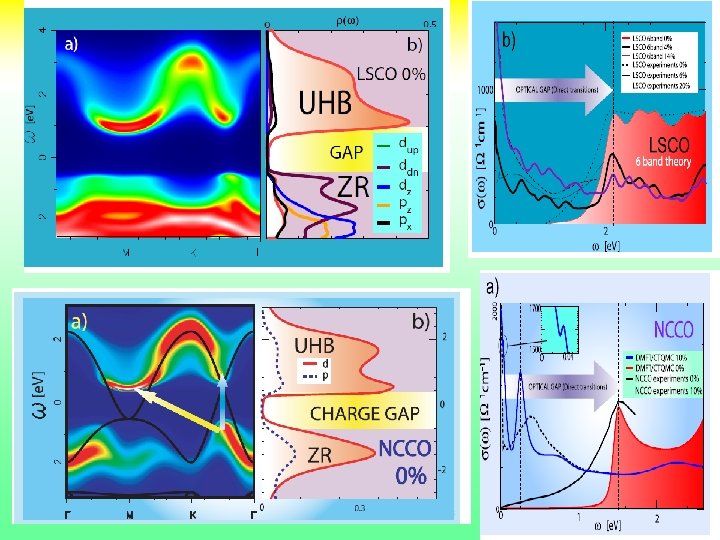
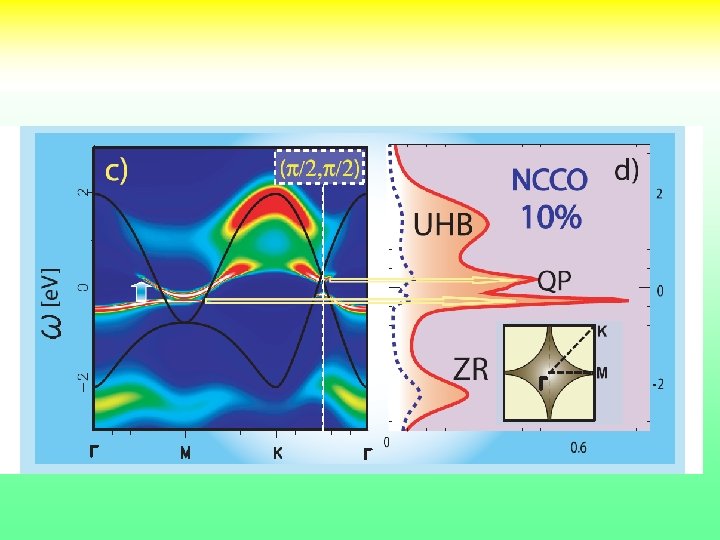
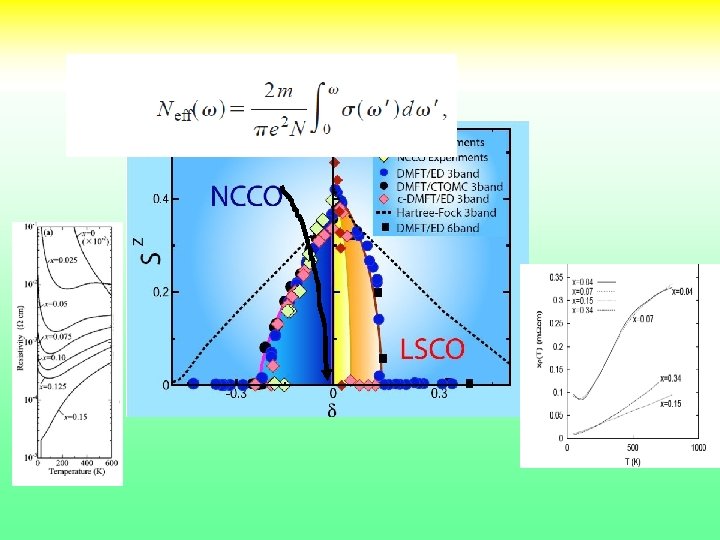
Electron and Hole Doped Cuprates : Similar but Yet Apical Different oxygen NCCO : Robust AF Phase Comensurate Magnetism Lower Tc T^2 resistivity. Non monotonic angle dependence of SC order parameter ……… Review: Armitage Fournier Green (2009) 1

Fundamental questions still unresolved • Important degrees of freedom at different energy scales [ dx 2 -y 2, px py, pz, dz 2 ] • Relevant effective hamiltonians, one band multiband, etc. • Mechanism of the superconductivity [ phonons, spin fluctuations, charge fluctuations, critical fluctuations, …. ] • How to describe the underlying normal state which does not fit in the fermi liquid paradigm (reference system) experiments. • Difference among different families, electron 19 vs hole doped. [ t, t’ fermi surfaces, …. ]

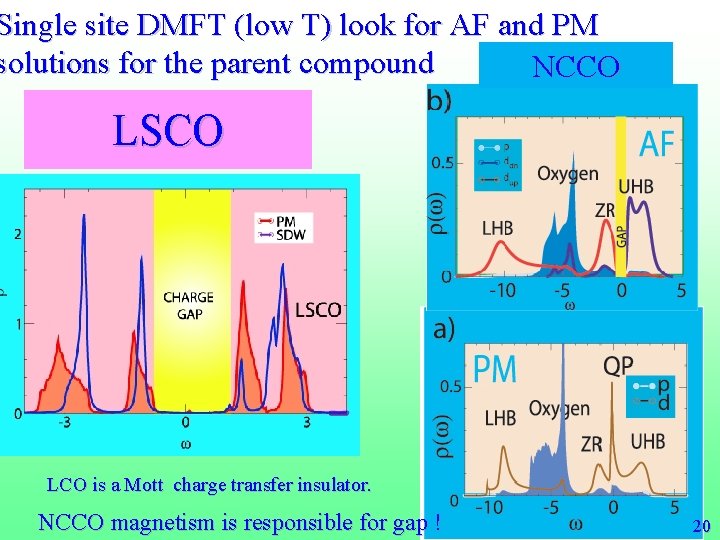
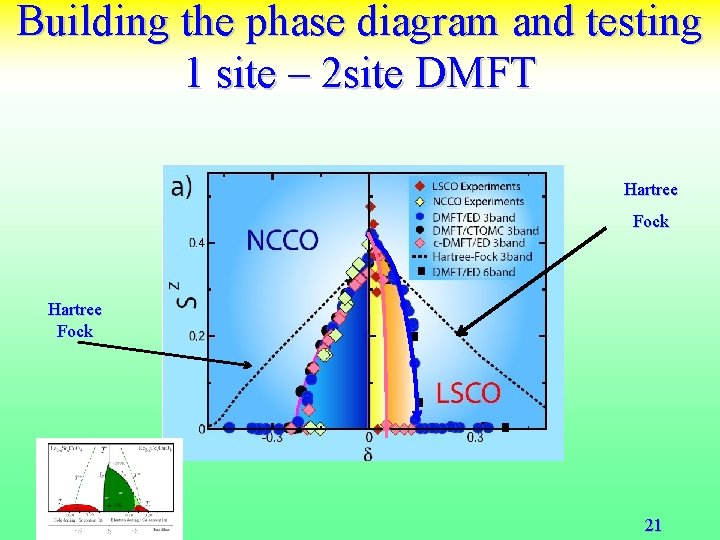
Single site DMFT (low T) look for AF and PM solutions for the parent compound NCCO LSCO LCO is a Mott charge transfer insulator. NCCO magnetism is responsible for gap ! 20

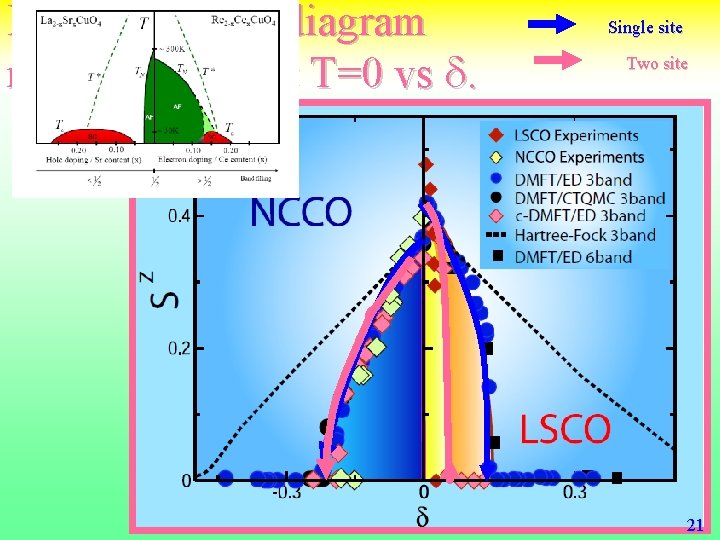
Building phase diagram magnetization at T=0 vs d. Single site Two site 21

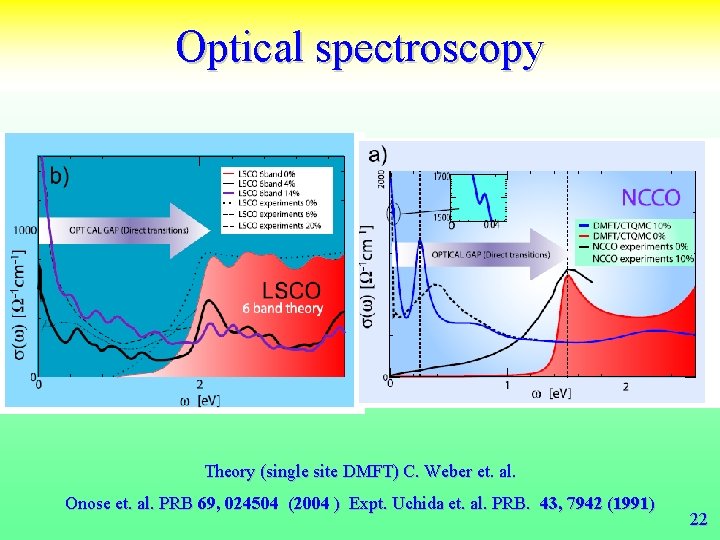
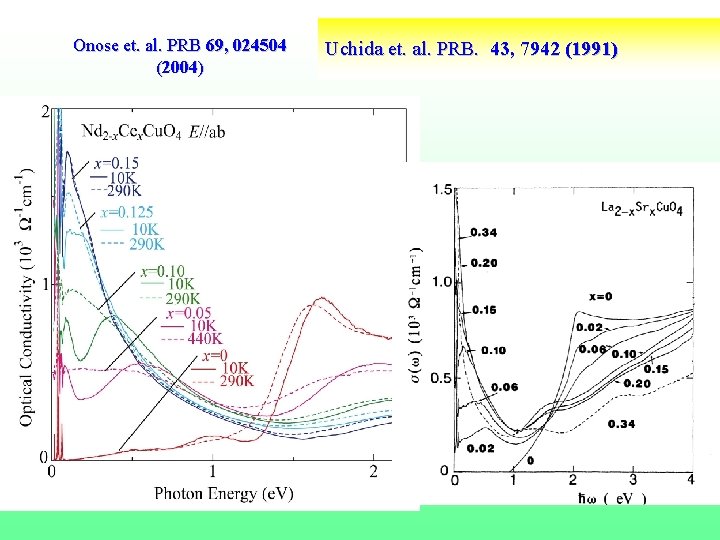
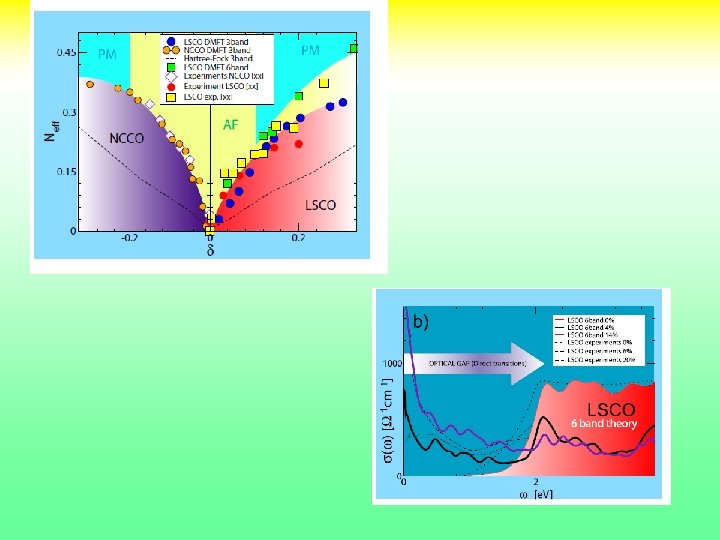
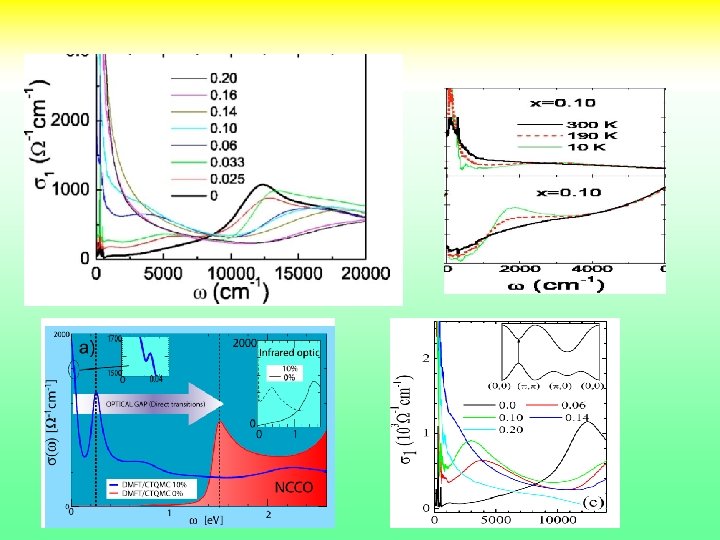
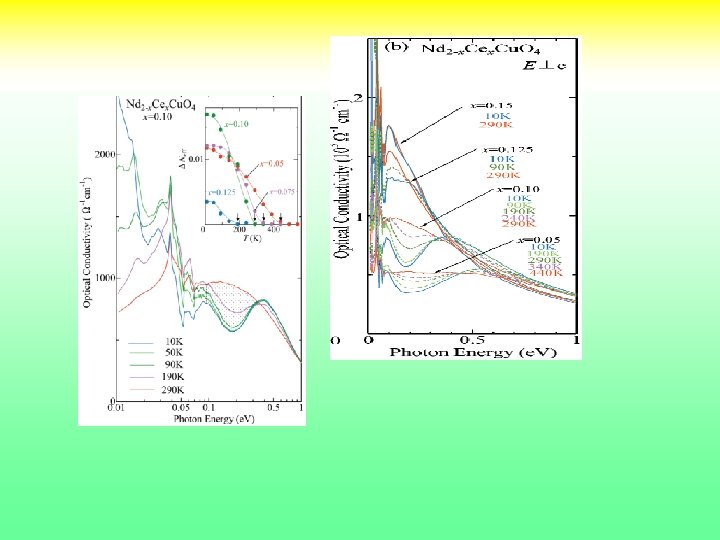
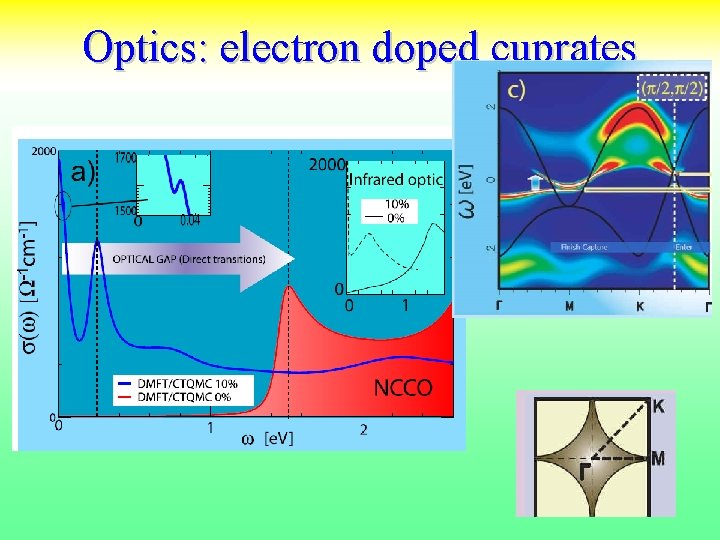
Optical spectroscopy Theory (single site DMFT) C. Weber et. al. Onose et. al. PRB 69, 024504 (2004 ) Expt. Uchida et. al. PRB. 43, 7942 (1991) 22

Optical Spectral Weights in LSCO and NCCO (up to 1. 5 ev) [xx]Y. Onose et al. , Phys. Rev. B, 69, 024504 (2004). [xx] S. Uchida et al. , Phys. Rev. B 43, 7942 (1991). [xx]S. Lupi et al. , Jour of superconductivity 17, 131 (2004). 23

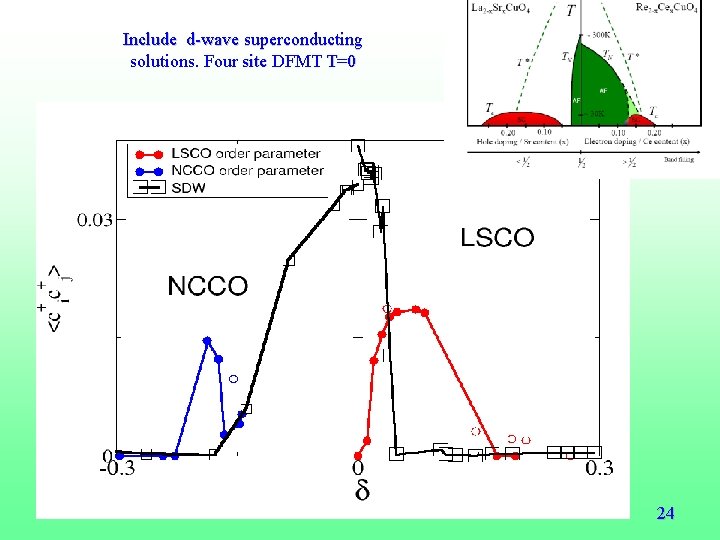
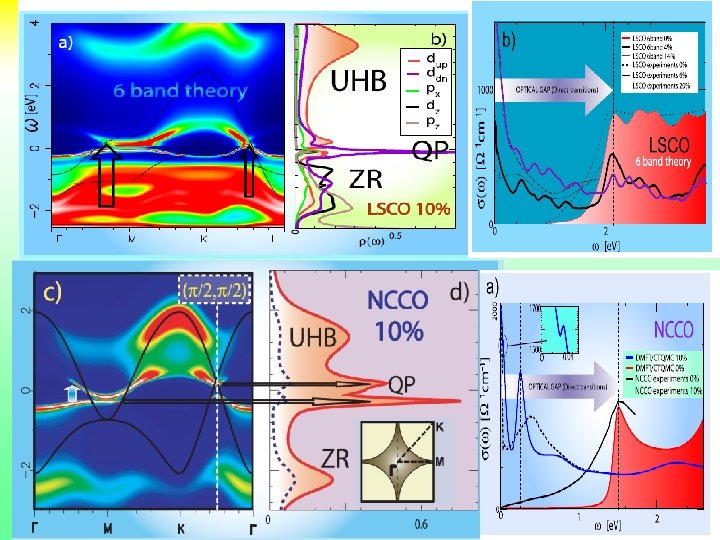
Include d-wave superconducting solutions. Four site DFMT T=0 Zero Temperature Moment 24

Conclusions LDA+DMFT NCCO vs LSCO • Good agreement with many subtle experimental features in NCCO even within single site DMFT. • No need to use x dependent values of the interaction U • In general, better modeling with DMFT (more sites, more orbitals etc ) better results. • Strength of correlations (as quantified by single site DMFT) the most fundamental difference between NCCO and LSCO compounds. • NCCO ( D < Dc 2 )and LSCO (D > Dc 2)straddle the Zaanen Sawatsky Allen localization delocalization boundary. • Can be traced to the absence of apical oxygen in NCCO (structure property relation). • Introduces subtle differences in the metallization process and interplay of magnetism and superconductivity. 25

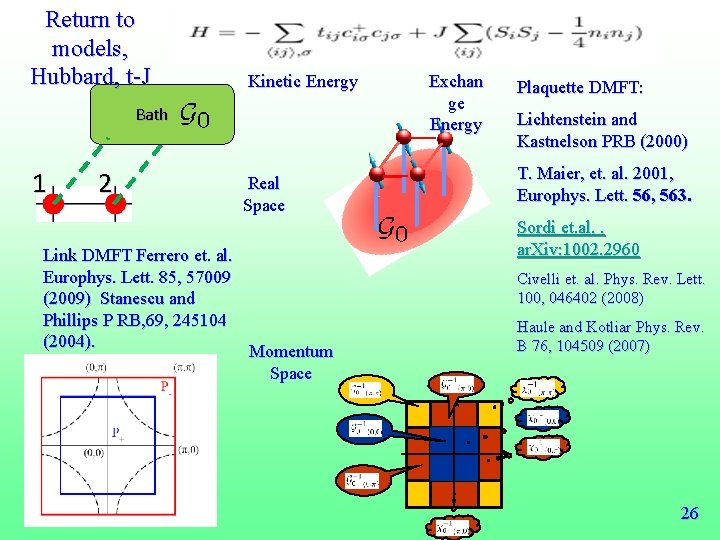
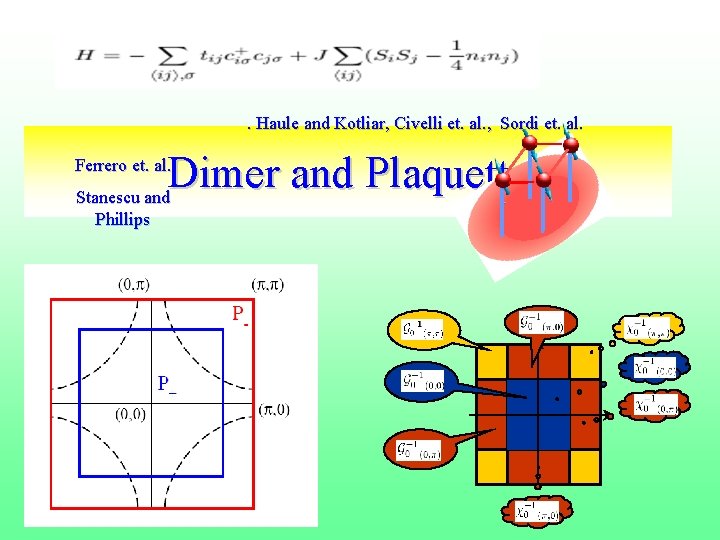
Return to models, Hubbard, t-J Kinetic Energy Bath 1 2 Real Space Link DMFT Ferrero et. al. Europhys. Lett. 85, 57009 (2009) Stanescu and Phillips P RB, 69, 245104 (2004). Momentum Space Exchan ge Energy Plaquette DMFT: Lichtenstein and Kastnelson PRB (2000) T. Maier, et. al. 2001, Europhys. Lett. 56, 563. Sordi et. al. . ar. Xiv: 1002. 2960 Civelli et. al. Phys. Rev. Lett. 100, 046402 (2008) Haule and Kotliar Phys. Rev. B 76, 104509 (2007) 26

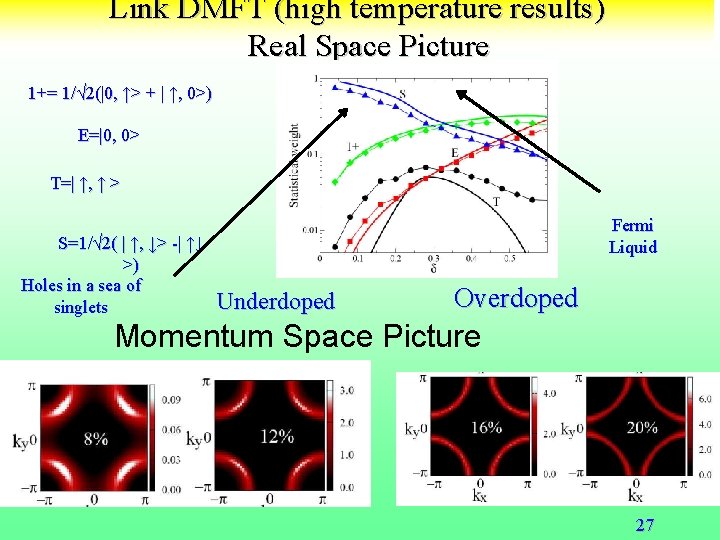
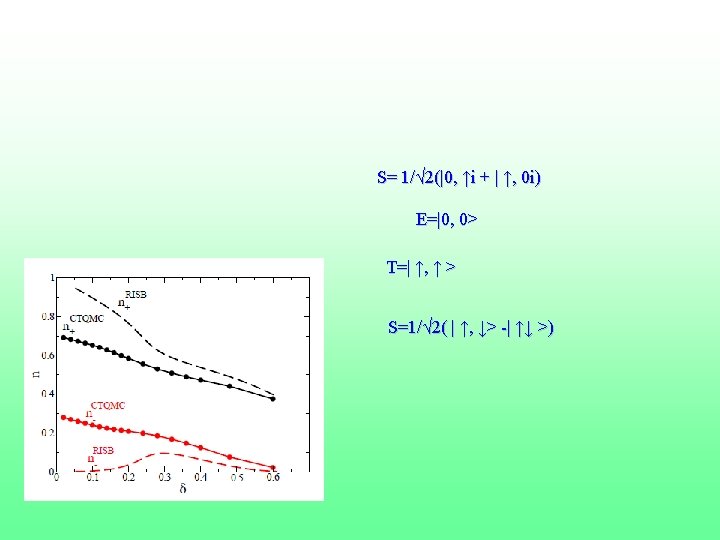
Link DMFT (high temperature results) Real Space Picture 1+= 1/√ 2(|0, ↑> + | ↑, 0>) E=|0, 0> T=| ↑, ↑ > S=1/√ 2( | ↑, ↓> -| ↑↓ >) Holes in a sea of singlets Fermi Liquid Underdoped Overdoped Momentum Space Picture 27

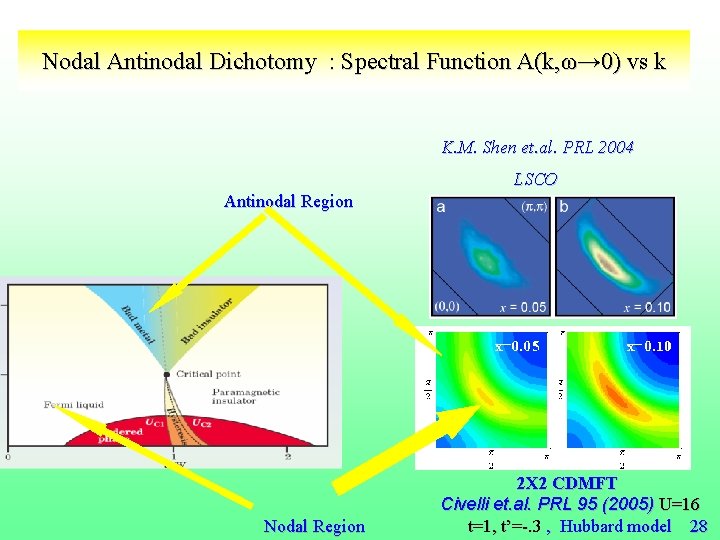
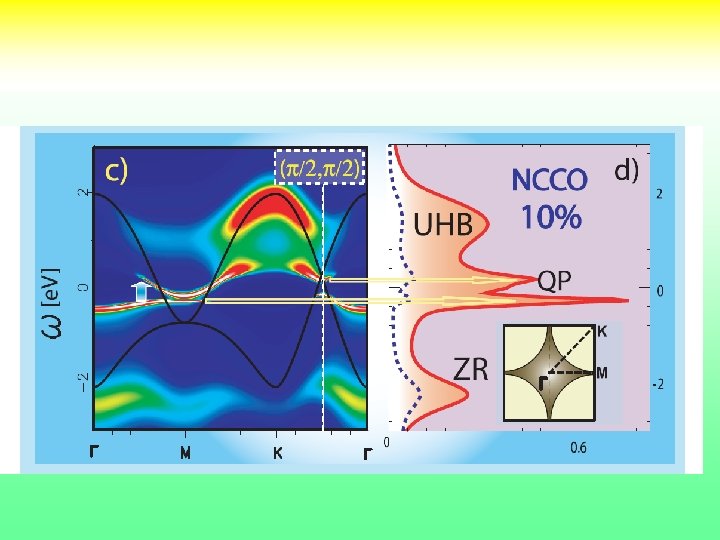
Nodal Antinodal Dichotomy : Spectral Function A(k, ω→ 0) vs k K. M. Shen et. al. PRL 2004 LSCO Antinodal Region Nodal Region 2 X 2 CDMFT Civelli et. al. PRL 95 (2005) U=16 t=1, t’=-. 3 , Hubbard model 28

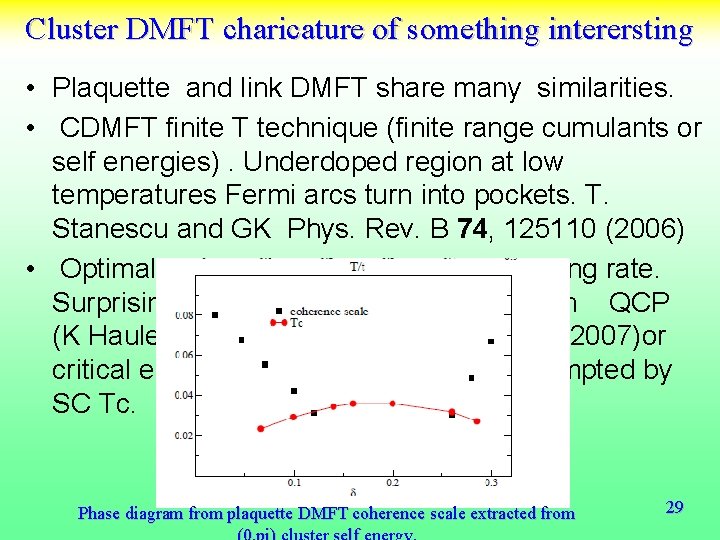
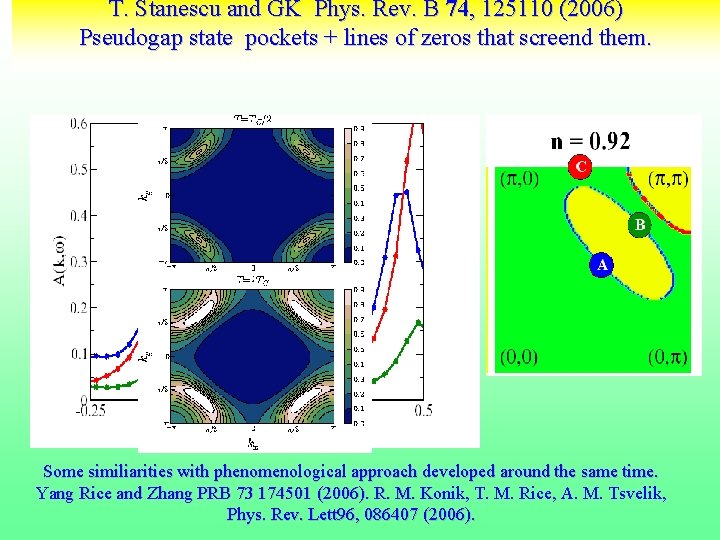
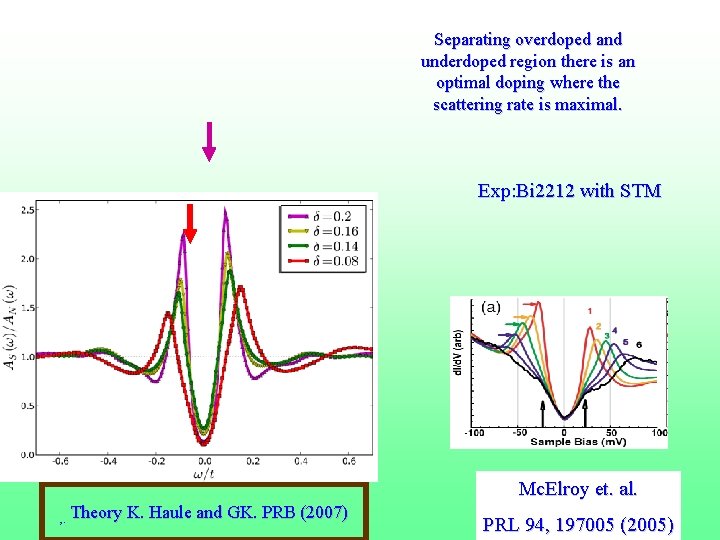
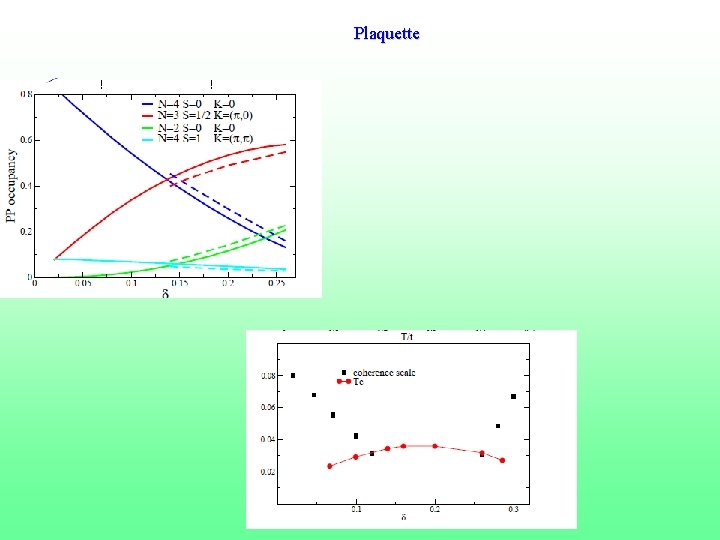
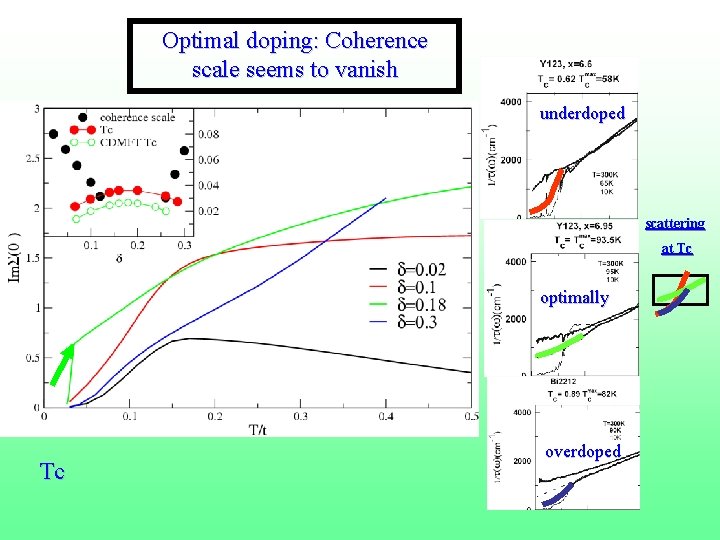
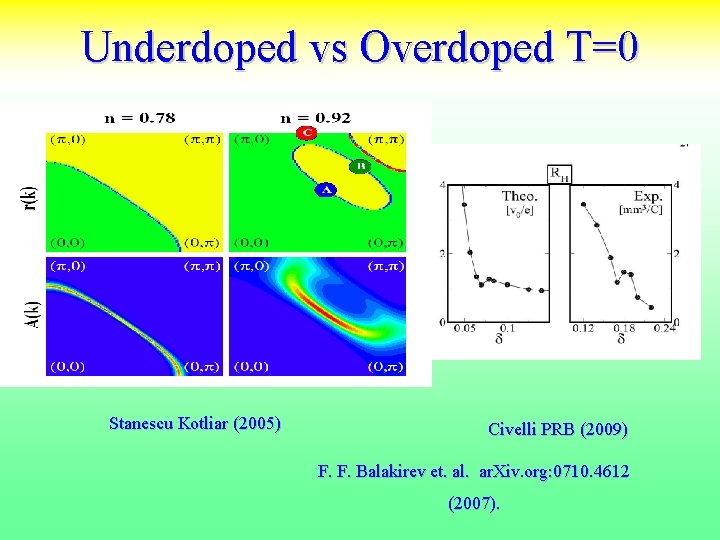
Cluster DMFT charicature of something interersting • Plaquette and link DMFT share many similarities. • CDMFT finite T technique (finite range cumulants or self energies). Underdoped region at low temperatures Fermi arcs turn into pockets. T. Stanescu and GK Phys. Rev. B 74, 125110 (2006) • Optimal doping. Maximum in the scattering rate. Surprising particle hole symmetry. Hidden QCP (K Haule and G. Kotliar PRB 76, 104509 (2007)or critical endpoint (Sordi et. al. 2010)) preempted by SC Tc. Phase diagram from plaquette DMFT coherence scale extracted from 29

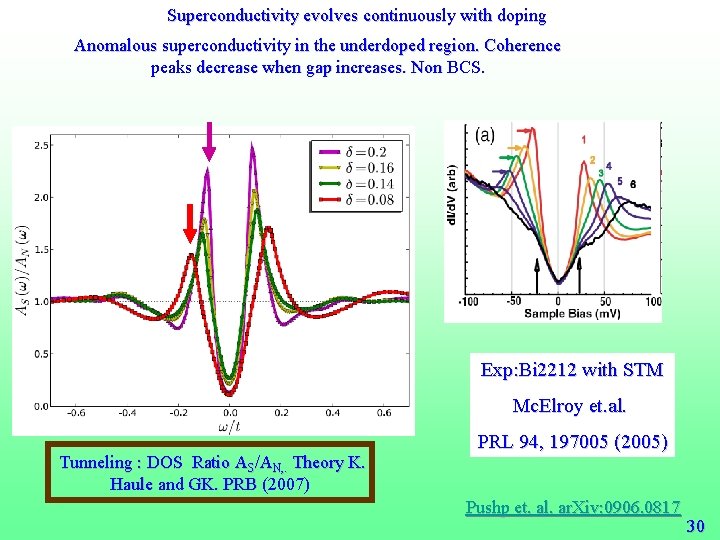
Superconductivity evolves continuously with doping Anomalous superconductivity in the underdoped region. Coherence peaks decrease when gap increases. Non BCS. Exp: Bi 2212 with STM Mc. Elroy et. al. Tunneling : DOS Ratio AS/AN, . Theory K. Haule and GK. PRB (2007) PRL 94, 197005 (2005) Pushp et. al. ar. Xiv: 0906. 0817 30

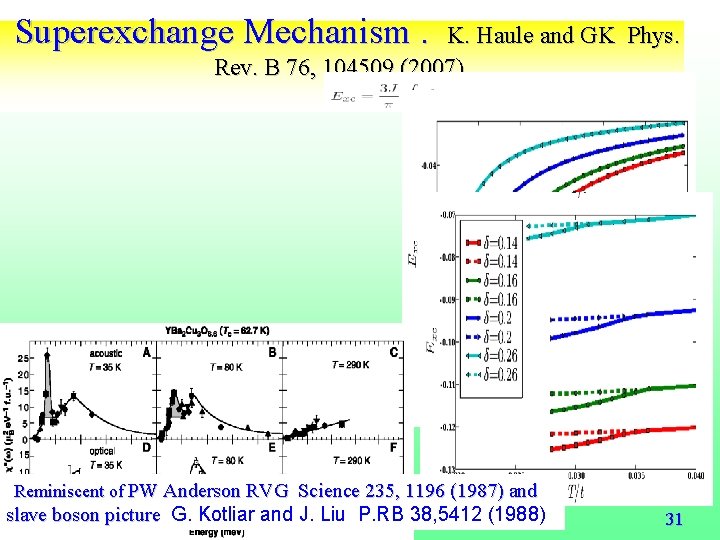
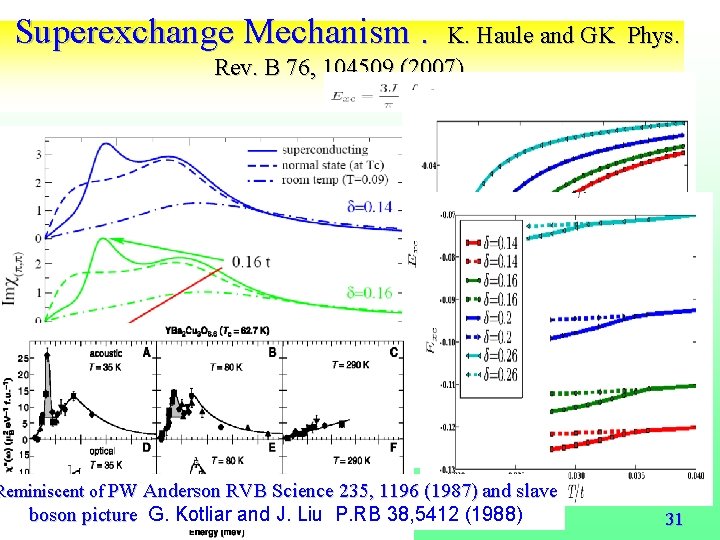
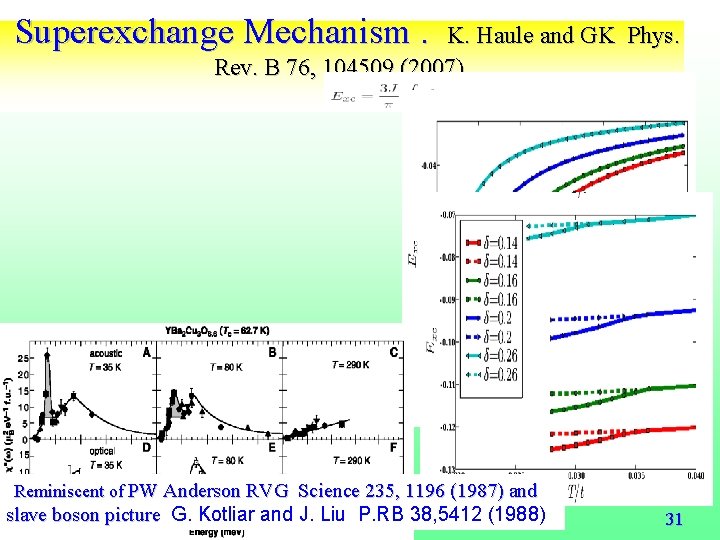
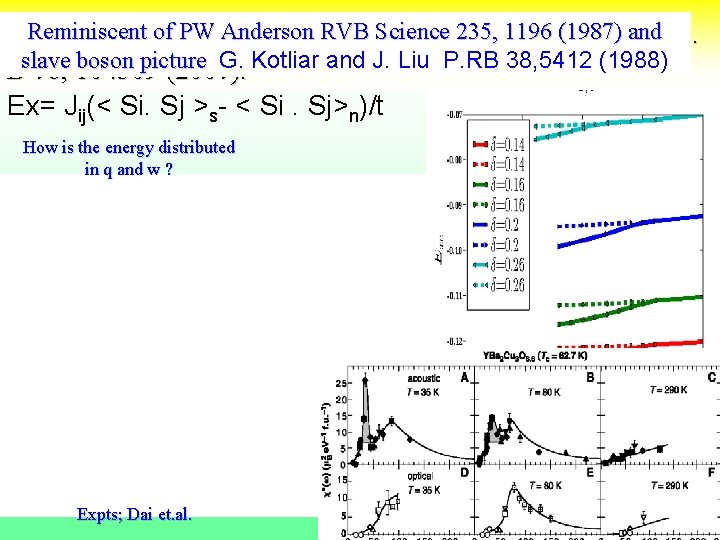
Superexchange Mechanism. K. Haule and GK Phys. Rev. B 76, 104509 (2007). D. J. Scalapino and S. R. White, Phys. Rev. B 58, 8222 (1998). Reminiscent of PW Anderson RVG Science 235, 1196 (1987) and slave boson picture G. Kotliar and J. Liu P. RB 38, 5412 (1988) 31

Conclusion / Outlook • Correlated Electron Systems: fundamental questions, promising applications. Huge phase space • DMFT (simple ? ) framework to think about electrons in solids and compute their properties. • Many succesful applications to many materials for which cannot be treated with other techniques. • In use for many materials by many groups. Qualitative and quantitative system specific results gives us confidence in the method. Example of actinide series, cuprates. • Needed: progress in implementation! • DMFT treats local correlation well but ignores non linear interactions among long wavelength modes and topological defects and other fluctuation effects. Limited k dependence [Connection with other approaches to strong correlation] • Starting point for more sophisticated treatments [ including long wavelength modes and their interactions as in. Stat mech] 32

Realistic DMFT as a tool for material exploration Separates essential ingredients [e. g. phonons, orbitals, structure etc. ] responsible for an effect. Compare different “states” of the system for the same value of parameters. Understand Mechanism for ordering. Bridge between atomic information and physical and spectroscopical properties. [Structure-Property relation Design] • New arenas Interfaces, junctions heterostructures, artificial materials containing correlated electrons • Grand challenge: using theory and computation to accelerate discoveries in strongly correlated electron systems. 32

Thank you for your attention!

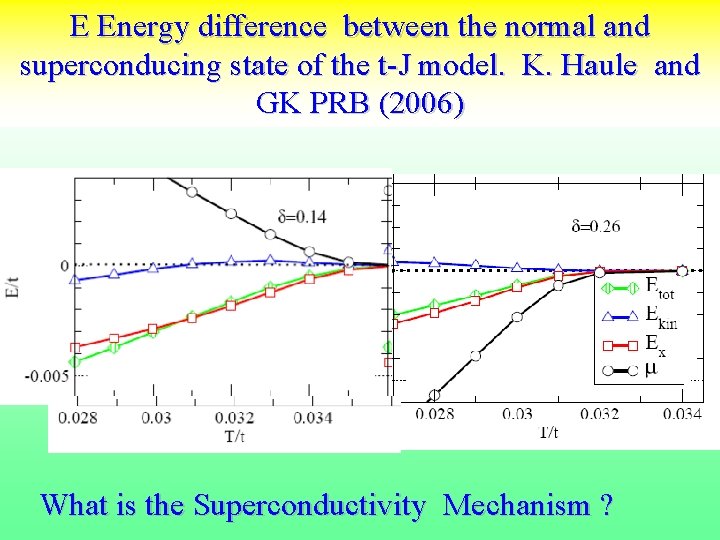
E Energy difference between the normal and superconducing state of the t-J model. K. Haule and GK PRB (2006) What is the Superconductivity Mechanism ?

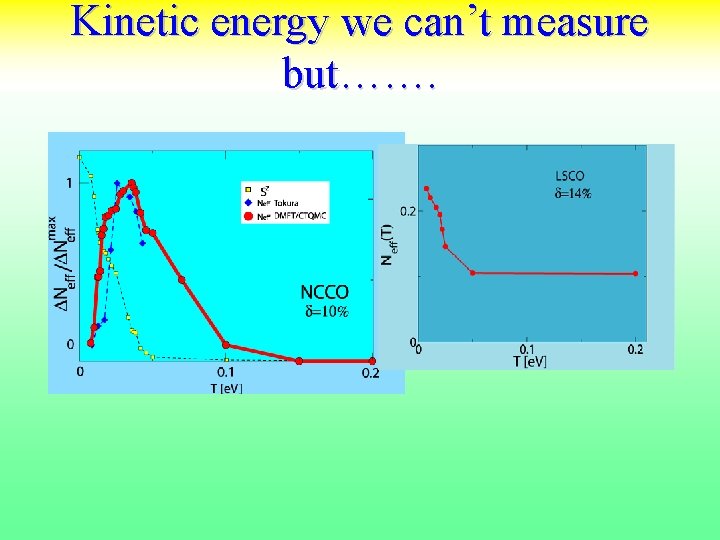
Optics and RESTRICTED SUM RULES [Ekin]n is only defined for T> Tc, while [Ekin]s exists only for T<Tc Experiment: use of this equation implies extrapolation. Theory : use of this equation implies of mean field picture to continue the normal state below Tc.

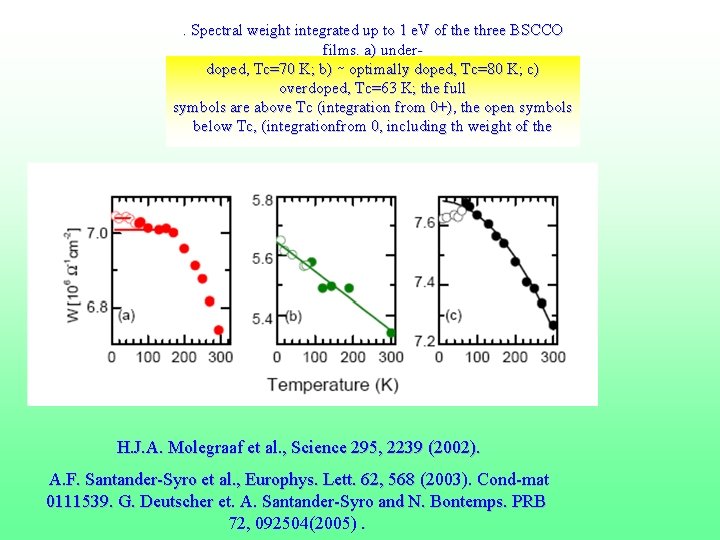
. Spectral weight integrated up to 1 e. V of the three BSCCO films. a) underdoped, Tc=70 K; b) ∼ optimally doped, Tc=80 K; c) overdoped, Tc=63 K; the full symbols are above Tc (integration from 0+), the open symbols below Tc, (integrationfrom 0, including th weight of the superfuid). H. J. A. Molegraaf et al. , Science 295, 2239 (2002). A. F. Santander-Syro et al. , Europhys. Lett. 62, 568 (2003). Cond-mat 0111539. G. Deutscher et. A. Santander-Syro and N. Bontemps. PRB 72, 092504(2005).

Difficulties Technical Issues • 2 x 2 cluster DMFT equations are considerably harder to solve and to interpret than single site DMFT. • Uniqueness: no unique formulation of cluster DMFT • Realistic implementations ARE demanding. Landscape of DMFT Solutions Problem Even within the same scheme at low T. In some region of parameters of the Hamiltonian, there at low temperature many solutions to the DMFT equations with different broken symmetries and ever increasing unite cells. No unique approach to expand around DMFT.

Correlated Superconductivity • New concepts and techniques to treat highly incoherent normal state and the superconductivity that emerges from it. • Coherence incoherence crossover, lines of zeros, momentum space differentiation, …… • Proximity to the Mott transition, accounts for many observations in correlated superconductors. • Still further developments are needed to improve cluster dynamical mean field theories (k space resolution) • Separates local mean field effects from fluctuation effects, superconducting fluctuations[ Nernst region etc. ] Fluctuations around mean field.

T. Stanescu and GK Phys. Rev. B 74, 125110 (2006) Pseudogap state pockets + lines of zeros that screend them. Some similiarities with phenomenological approach developed around the same time. Yang Rice and Zhang PRB 73 174501 (2006). R. M. Konik, T. M. Rice, A. M. Tsvelik, Phys. Rev. Lett 96, 086407 (2006).

Superexchange Mechanism. K. Haule and GK Phys. Rev. B 76, 104509 (2007). D. J. Scalapino and S. R. White, Phys. Rev. B 58, 8222 (1998). Reminiscent of PW Anderson RVB Science 235, 1196 (1987) and slave boson picture G. Kotliar and J. Liu P. RB 38, 5412 (1988) 31

Superexchange Mechanism. K. Haule and GK Phys. Rev. B 76, 104509 (2007). D. J. Scalapino and S. R. White, Phys. Rev. B 58, 8222 (1998). Reminiscent of PW Anderson RVG Science 235, 1196 (1987) and slave boson picture G. Kotliar and J. Liu P. RB 38, 5412 (1988) 31

Reminiscent of PW Anderson RVB Science Superexchange Mechanism? . K. Haule 235, and 1196 GK(1987) Phys. and Rev. boson picture G. Kotliar and J. Liu P. RB 38, 5412 (1988) Bslave 76, 104509 (2007). Ex= Jij(< Si. Sj >s- < Si. Sj>n)/t How is the energy distributed in q and w ? D. J. Scalapino and S. R. White, Phys. Rev. B 58, 8222 (1998). Expts; Dai et. al.

Onose et. al. PRB 69, 024504 (2004) Uchida et. al. PRB. 43, 7942 (1991)

“Matthias’s Rules” for High Tc • Metals. Must have d electrons (not just s s-p, nor f). Stay away from oxides. • High symmetry is good, cubic is best. Nb 3 Sn • Certain electron concentrations are favored (look for peak in density of states at Fermi level) • Stay away from theorists • “ Do not follow my rules “ 29

Thanks !!!

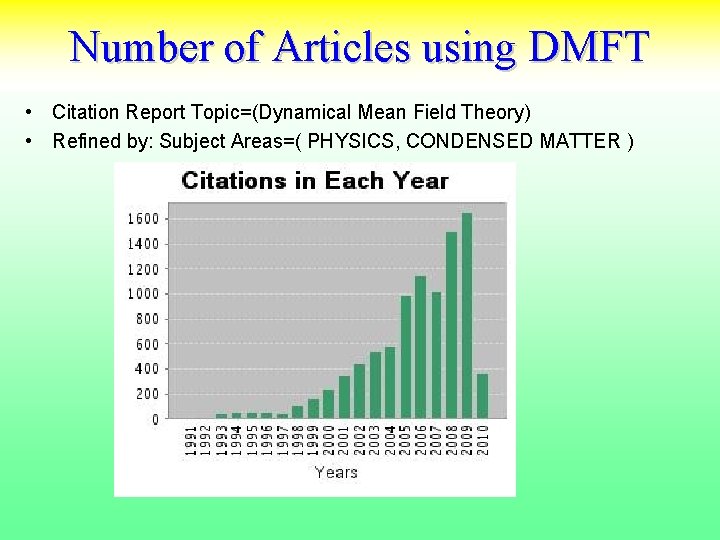
Number of Articles using DMFT • Citation Report Topic=(Dynamical Mean Field Theory) • Refined by: Subject Areas=( PHYSICS, CONDENSED MATTER )

Separating overdoped and underdoped region there is an optimal doping where the scattering rate is maximal. Exp: Bi 2212 with STM Mc. Elroy et. al. , . Theory K. Haule and GK. PRB (2007) PRL 94, 197005 (2005)

Plaquette

Optimal doping: Coherence scale seems to vanish underdoped scattering at Tc optimally Tc overdoped

Comments What about broken symmetries and their quantum critical points ? Charge stripes, spin stripes, staggered currents, uniform currents, bond density waves, waves spin nematic order , spin glass, bond glass, have all been observed. Connections with S. Sachdev ar. Xiv: 0910. 0846 Can all be studied with CDMFT, given a well defined hamiltonian. But first things first, local physics, high temperature regimes less sensitive to details. Isolate the qualitative aspects that follow from the proximity to the Mott transition, from those that require specific broken symmetries. For example: formation of arcs. Competing short range order. What about the electron phonon interaction, disordered introduced by dopants, oxygen orbitals, realistic band structure which are out there ? Can be studied with LDA+DMFT, GW+DMFT to understand chemical trends within different families.

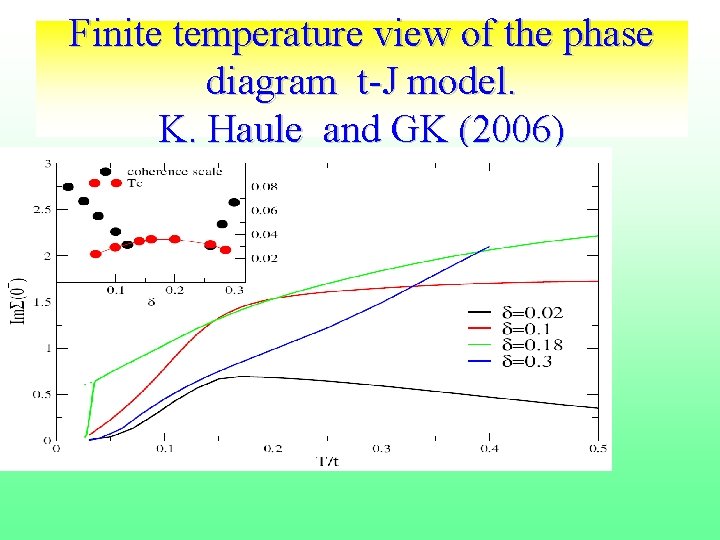
Finite temperature view of the phase diagram t-J model. K. Haule and GK (2006)

La. OFe. As 1111 9

VO 2 Nax Co. O 2 YBa 2 Cu 3 O 7 5

Underdoped vs Overdoped T=0 Stanescu Kotliar (2005) Civelli PRB (2009) F. F. Balakirev et. al. ar. Xiv. org: 0710. 4612 (2007).

Finding interesting correlated materials Serendipity + Edisonian approach An aptitude for making desirable discoveries by accident The Edisonian approach to innovation is characterized by trial and error discovery rather than a systematic theoretical approach. In developing the carbon microphone that became the basis of telephones of the next hundred years Edison and his co-workers tried hundreds of substances. 6

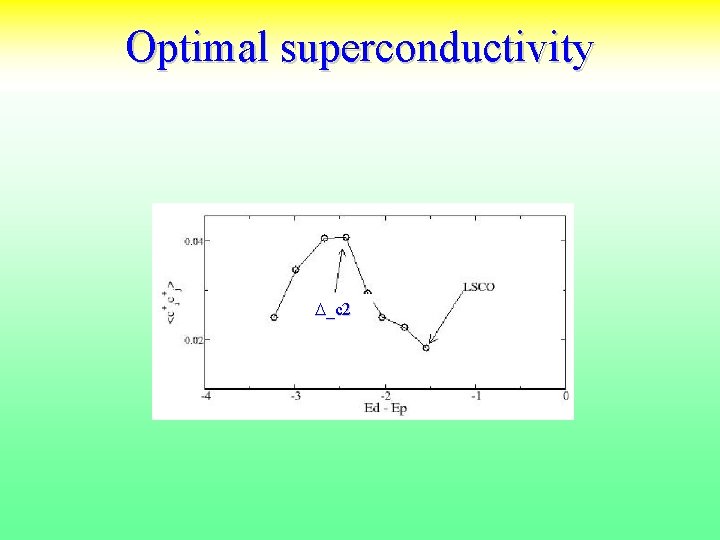
Optimal superconductivity D_c 2

Kinetic energy we can’t measure but…….

Return to models (Hubbard and t-J) • Unclear if they are superconducting in thermodynamical limit. • Have Mott transition that can be studied in plaquette DMFT. Important lessons that will impact further realistic studies. • Concentrate on robust states. AF, SC, PM, PI. • There are of course ordered states [current order, nematic order, stripe order, staggered flux order, etc. ]

Key Question Within the Stated Assumptions (i. e. Model Hamiltonians and Plaquette DMFT)what is the mechanims for superconductivity. How it is connected to the underlying “normal” state

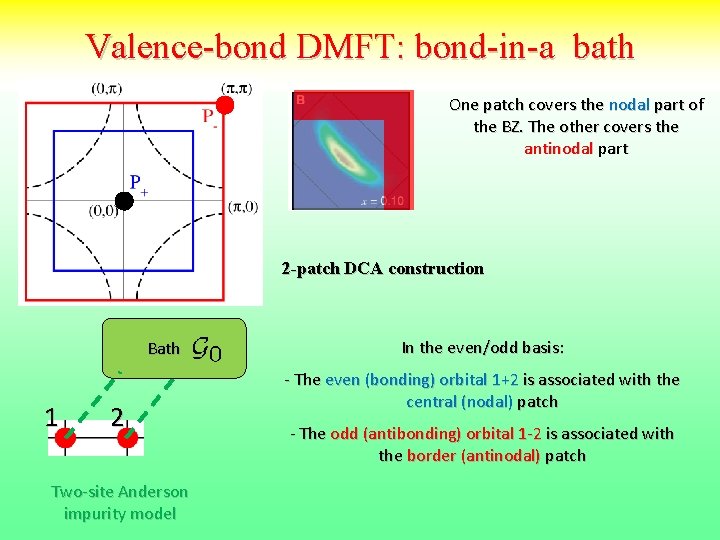
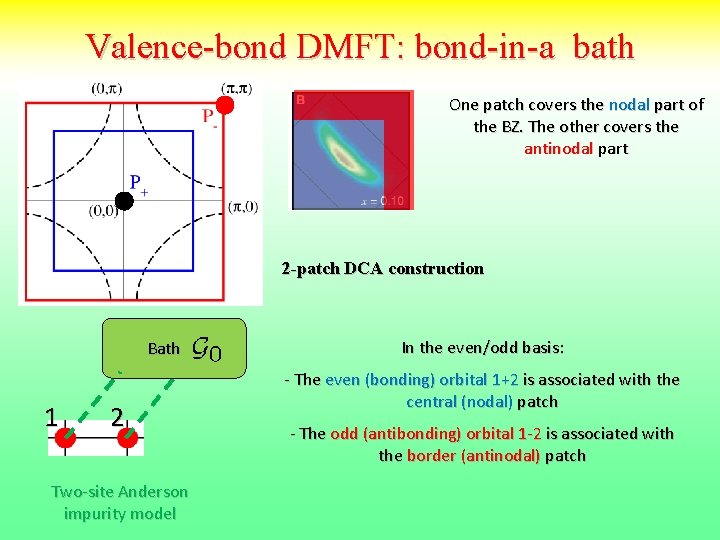
Valence-bond DMFT: bond-in-a bath One patch covers the nodal part of the BZ. The other covers the antinodal part 2 -patch DCA construction Bath 1 2 Two-site Anderson impurity model In the even/odd basis: - The even (bonding) orbital 1+2 is associated with the central (nodal) patch - The odd (antibonding) orbital 1 -2 is associated with the border (antinodal) patch

Valence-bond DMFT: bond-in-a bath One patch covers the nodal part of the BZ. The other covers the antinodal part 2 -patch DCA construction Bath 1 2 Two-site Anderson impurity model In the even/odd basis: - The even (bonding) orbital 1+2 is associated with the central (nodal) patch - The odd (antibonding) orbital 1 -2 is associated with the border (antinodal) patch

. Haule and Kotliar, Civelli et. al. , Sordi et. al. Dimer and Plaquette Stanescu and Ferrero et. al. Phillips

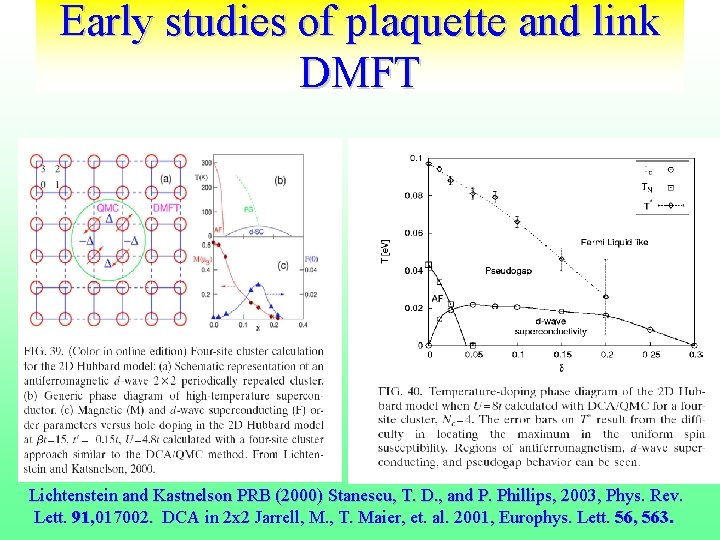
Early studies of plaquette and link DMFT Lichtenstein and Kastnelson PRB (2000) Stanescu, T. D. , and P. Phillips, 2003, Phys. Rev. Lett. 91, 017002. DCA in 2 x 2 Jarrell, M. , T. Maier, et. al. 2001, Europhys. Lett. 56, 563.

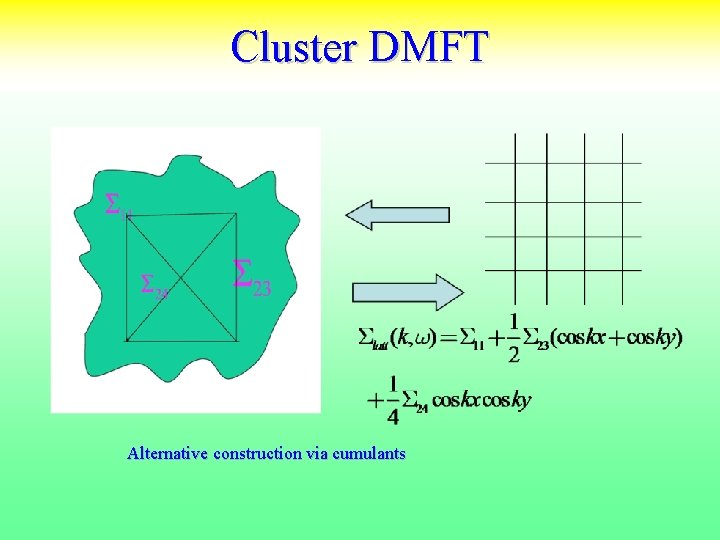
Cluster DMFT Alternative construction via cumulants

Previous methods fail near Pu • Spin Density functional theory: Pu , Am, magnetic, large orbital and spin moments. • Experiments (Lashley et. al. 2005, Heffner et al. (2006)): d Pu is non magnetic. No static or fluctuating moments. Susceptibility, specific heat in a field, neutron quasielastic and inelastic scattering, muon spin resonance… • Paramagnetic LDA underestimates Volume of d Pu. • Thermodynamic and transport properties similar to strongly correlated materials. • Plutonium: correlated paramagnetic metal.

Optics and RESTRICTED SUM RULES Below energy Low energy sum rule can have T and doping dependence. For nearest neighbor it gives the kinetic energy. Use it to extract changes in KE in superconducing state

Plutonium

Plutonium: an anomalous metal

Photoemssion (expt. Arko, theory Shim. Gouder , Havela PRB al. science) 2002, 2003

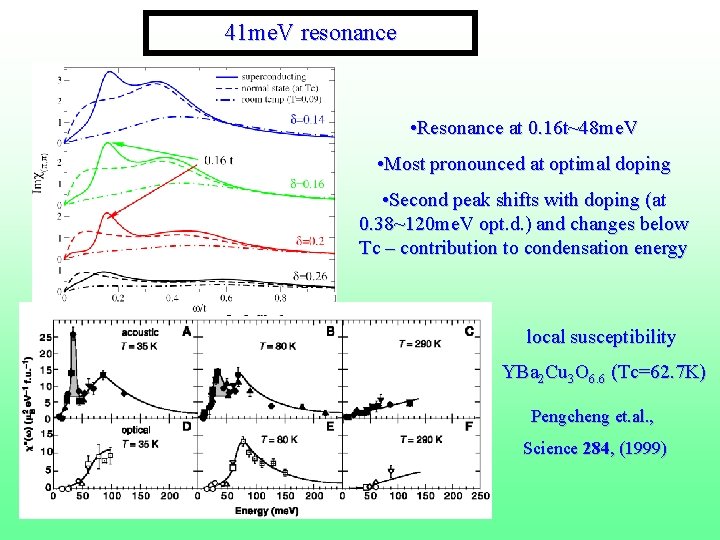
41 me. V resonance • Resonance at 0. 16 t~48 me. V • Most pronounced at optimal doping • Second peak shifts with doping (at 0. 38~120 me. V opt. d. ) and changes below Tc – contribution to condensation energy local susceptibility YBa 2 Cu 3 O 6. 6 (Tc=62. 7 K) Pengcheng et. al. , Science 284, (1999)

Dynamical Mean Field Theory • Describes the electron both in the itinerant (wave-like) and localized (particle-like) regimes and everything in between!. • Simpler reference systems to understand a problem. [e. g. harmonic oscillator] • Follow different mean field states (phases) Compare free energies properties. • Non Gaussian reference frame for correlated materials. • Reference frame can be cluster of sites CDMFT REVIEWS. Lichtenstein and Kastnelson PRB (2000) Stanescu, T. D. , and P. Phillips, 2003, Phys. Rev. Lett. 91, 017002. DCA in 2 x 2 Jarrell, M. , T. Maier, et. al. 2001, Europhys. Lett. 56, 563 CUMULANTS. REFERENCE. 11

Strongly Correlated Materials Not well described by either the fully localized picture (well separated atoms) or the band picture (weakly interacting bloch waves). . Materials for which the standard model of the solid state fails. Challenging non perturbative problem. Correlated variables Continuous discovery of interesting material and phenomena that did not fit the standard model of solid state physics. Heavy fermions (early 80’s) , high temperature superconductors (late 80’s), other transition metal oxides (cobaltates, manganites, vanadates…. ) 90’s …… high Tc in Fe. As based compounds (2009). Materials discovered by serendipity and the 4

Optics: electron doped cuprates

Building the phase diagram and testing 1 site – 2 site DMFT Hartree Fock 21