Strong tensor correlation in light nuclei with tensoroptimized

Strong tensor correlation in light nuclei with tensor-optimized antisymmetrized molecular dynamics (TOAMD) Takayuki MYO International symposium on “High-resolution Spectroscopy and Tensor interactions” (HST 15), Osaka, 2015. 11

Outline • Tensor Optimized Shell Model (TOSM) • Importance of 2 p 2 h excitation involving highmomentum component for tensor correlation • Applications to He, Li, Be isotopes • Tensor Optimized AMD (TOAMD) • Toward clustering with tensor correlation • Formulation given in PTEP 2015, 073 D 02 2

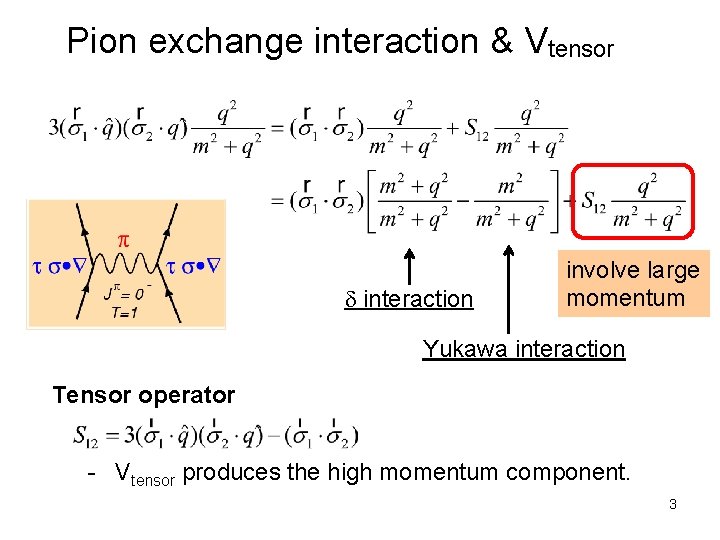
Pion exchange interaction & Vtensor d interaction involve large momentum Yukawa interaction Tensor operator - Vtensor produces the high momentum component. 3

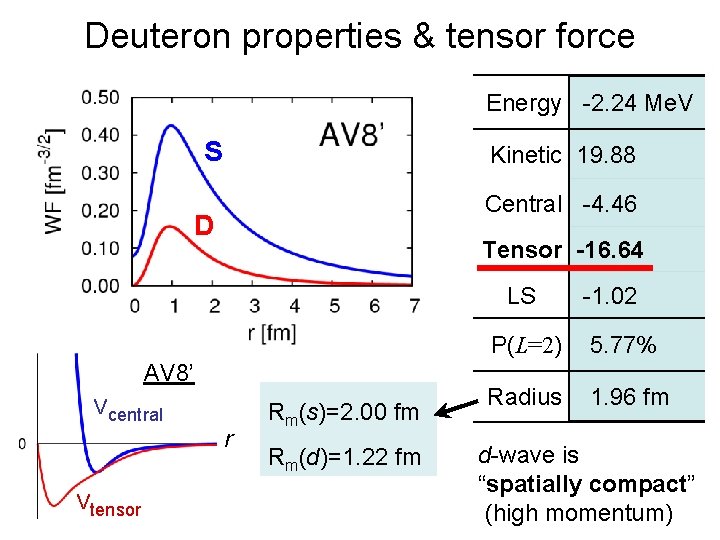
Deuteron properties & tensor force Energy -2. 24 Me. V S Kinetic 19. 88 Central -4. 46 D Tensor -16. 64 LS -1. 02 P(L=2) 5. 77% AV 8’ Vcentral Vtensor r Rm(s)=2. 00 fm Rm(d)=1. 22 fm Radius 1. 96 fm d-wave is “spatially compact” (high momentum)

Tensor-optimized shell model (TOSM) TM, Sugimoto, Kato, Toki, Ikeda PTP 117(2007)257 Shell model type configuration with mass number A (0 p 0 h+1 p 1 h+2 p 2 h) particle state Gaussian expansion for each orbit Gaussian basis function Hiyama, Kino, Kamimura PPNP 51(2003)223 c. m. excitation is excluded by Lawson’s method

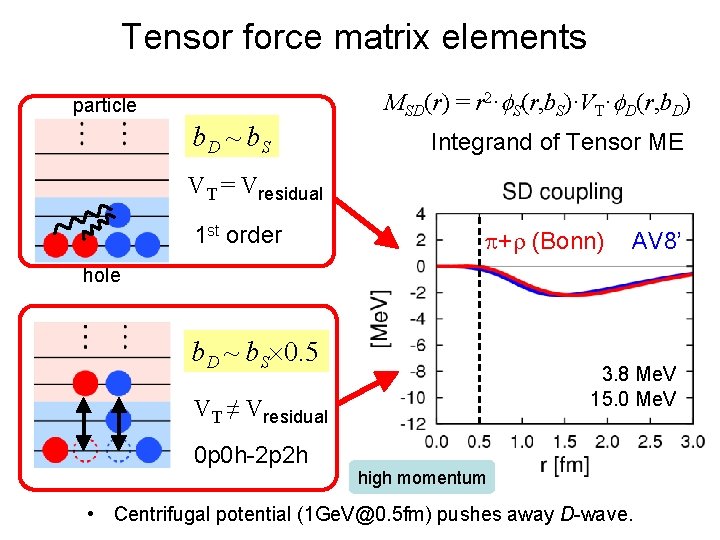
Tensor force matrix elements MSD(r) = r 2·f. S(r, b. S)·VT·f. D(r, b. D) particle b. D ~ b. S Integrand of Tensor ME VT = Vresidual 1 st order p+r (Bonn) AV 8’ hole b. D ~ b. S 0. 5 3. 8 Me. V 15. 0 Me. V VT ≠ Vresidual 0 p 0 h-2 p 2 h high momentum • Centrifugal potential (1 Ge. V@0. 5 fm) pushes away D-wave. 6

He, Li, Be isotopes in TOSM TM, A. Umeya, H. Toki, K. Ikeda PRC 84 (2011) 034315 TM, A. Umeya, H. Toki, K. Ikeda PRC 86 (2012) 024318 TM, A. Umeya, K. Horii, H. Toki, K. Ikeda PTEP (2014) 033 D 01 TM, A. Umeya, H. Toki, K. Ikeda PTEP (2015) 073 D 02 7

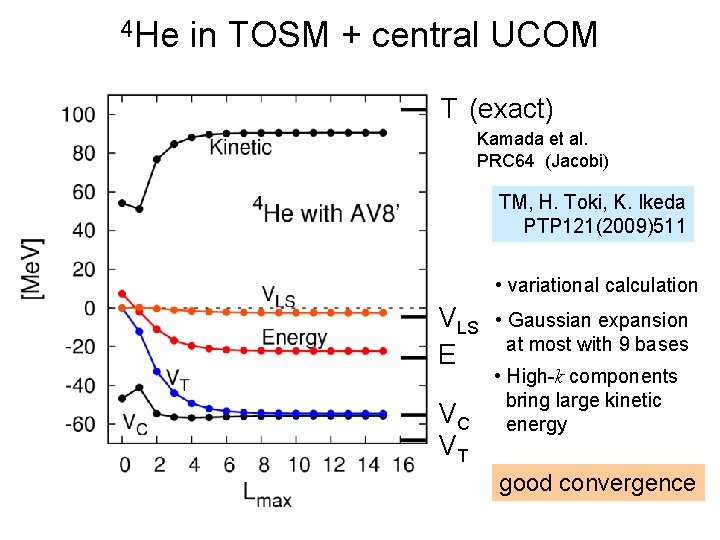
4 He in TOSM + central UCOM T (exact) Kamada et al. PRC 64 (Jacobi) TM, H. Toki, K. Ikeda PTP 121(2009)511 • variational calculation VLS E VC VT • Gaussian expansion at most with 9 bases • High-k components bring large kinetic energy good convergence

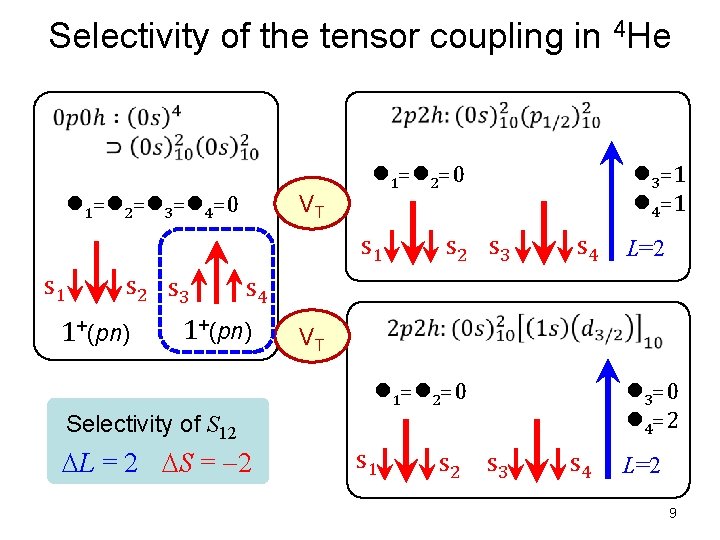
Selectivity of the tensor coupling in 4 He l 1=l 2=l 3=l 4=0 VT s 1 s 2 s 3 1+(pn) l 3=1 l 4=1 l 1=l 2=0 s 2 s 3 s 4 L=2 s 4 1+(pn) VT l 1=l 2=0 l 3=0 l 4=2 Selectivity of S 12 DL = 2 DS = 2 s 1 s 2 s 3 s 4 L=2 9

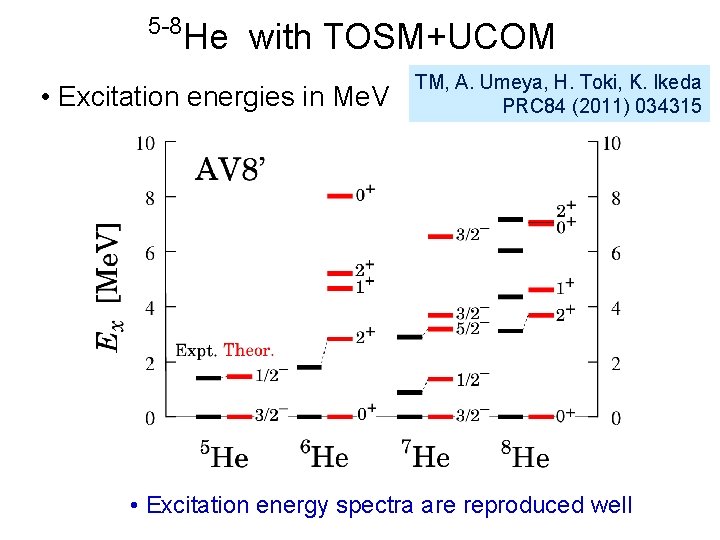
5 -8 He with TOSM+UCOM • Excitation energies in Me. V TM, A. Umeya, H. Toki, K. Ikeda PRC 84 (2011) 034315 • Excitation energy spectra are reproduced well

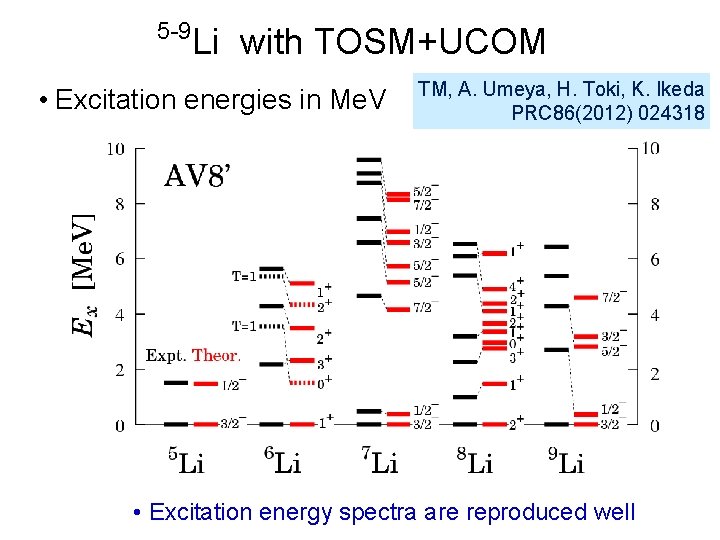
5 -9 Li with TOSM+UCOM • Excitation energies in Me. V TM, A. Umeya, H. Toki, K. Ikeda PRC 86(2012) 024318 • Excitation energy spectra are reproduced well

Radius of He & Li isotopes Expt TOSM with AV 8’ Halo Skin I. Tanihata et al. , PLB 289(‘ 92)261 O. A. Kiselev et al. , EPJA 25, Suppl. 1(‘ 05)215. A. Dobrovolsky, NPA 766(2006)1 G. D. Alkhazov et al. , PRL 78(‘ 97)231312 P. Mueller et al. , PRL 99(2007)252501

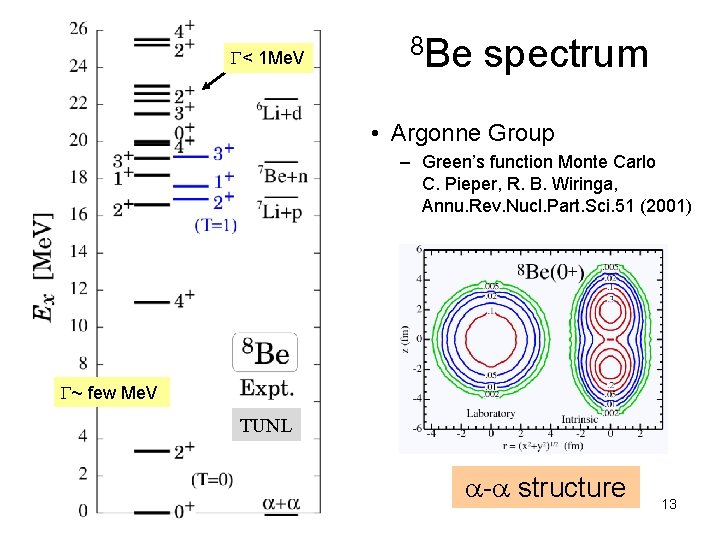
G< 1 Me. V 8 Be spectrum • Argonne Group – Green’s function Monte Carlo C. Pieper, R. B. Wiringa, Annu. Rev. Nucl. Part. Sci. 51 (2001) G~ few Me. V TUNL a-a structure 13

8 Be in TOSM AV 8’ • VT 1. 1, VLS 1. 4 – simulate 4 He benchmark (Kamada et al. , PRC 64) • correct level order (T=0, 1) • tensor contribution : T=0 > T=1 • a : 0 p 0 h+2 p 2 h with high-k – 2 a needs 4 p 4 h. – spatial asymptotic form of 2 a Expt. (TUNL) TOSM a a clustering 14 TOAMD

Tensor-Optimized Antisymmetrized Molecular Dynamics (TOAMD) TM, H. Toki, K. Ikeda, H. Horiuchi, T. Suhara, PTEP 2015, 073 D 02 Toward the clustering with tensor correlation explicitly 15

(TOAMD) 0 p 0 h 2 p 2 h Gaussian expansion tensor correlation short-range correlation

Formulation of TOAMD 0 p 0 h 2 p 2 h 4 p 4 h • 17

Matrix elements of multi-body operator Matrix elements range particle coordinate • centroid 2 -body FD VT FD 4 -body FD VT FD

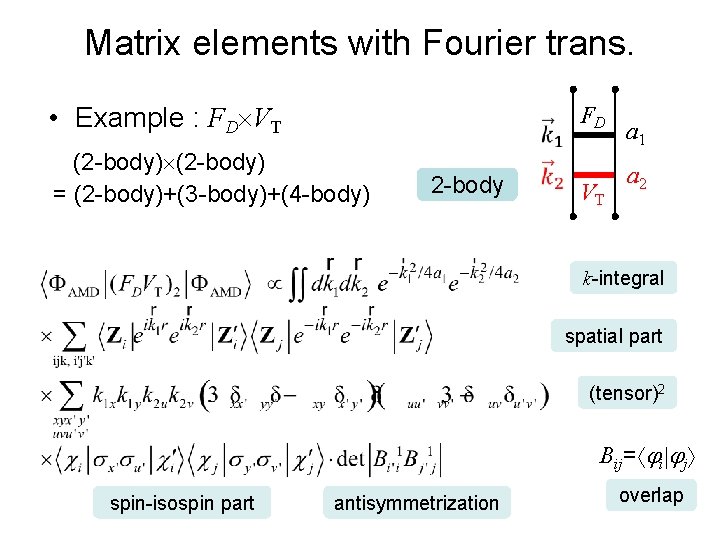
Matrix elements with Fourier trans. • Fourier transformation of the interaction V & FD, FS. – Y. Goto and H. Horiuchi, Prog. Theor. Phys. , 62 (1979) 662 – Gaussian expansion of V, FD, FS for relative motion – Multi-body operators are represented in the separable form for particle coordinates. – Three-body interaction can be treated in the same manner. single particle relative tensor-type overlap Quadratic + Linear terms of k 19

Matrix elements with Fourier trans. • Example : FD VT (2 -body) = (2 -body)+(3 -body)+(4 -body) 2 -body FD VT a 1 a 2 k-integral spatial part (tensor)2 Bij= i j spin-isospin part antisymmetrization overlap

Matrix elements with Fourier trans. • Example : FD VT (2 -body) = (2 -body)+(3 -body)+(4 -body) 3 -body FD a 1 V T a 2 k-integral spatial part (tensor)2 Bij= i j spin-isospin part antisymmetrization overlap 21

TOSM vs. TOAMD TOSM TOAMD 1 p 1 h, 2 p 2 h (single particle) Relative motion in FD, FS CM excitation Lawson method Nothing with single n Hole states harmonic oscillator basis Can optimize in each basis central-UCOM Correlation function, FS Correlation Short-range repulsion 22

Results • 2 -body FS T FS FD FD FS T VT FD others. . . 3 -body FS VT FD FD FD VT

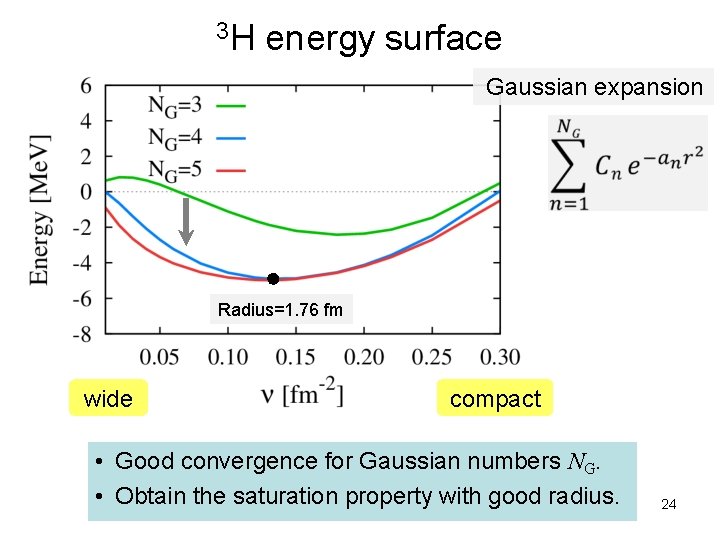
3 H energy surface Gaussian expansion Radius=1. 76 fm wide compact • Good convergence for Gaussian numbers NG. • Obtain the saturation property with good radius. 24

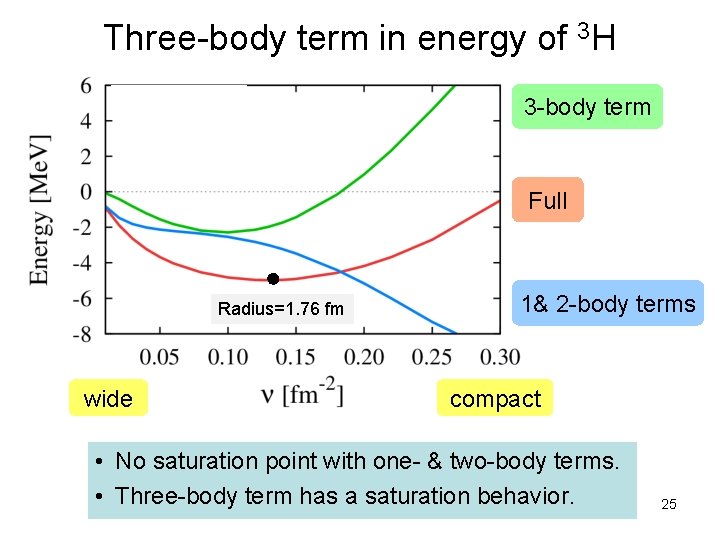
Three-body term in energy of 3 H 3 -body term Full Radius=1. 76 fm wide 1& 2 -body terms compact • No saturation point with one- & two-body terms. • Three-body term has a saturation behavior. 25

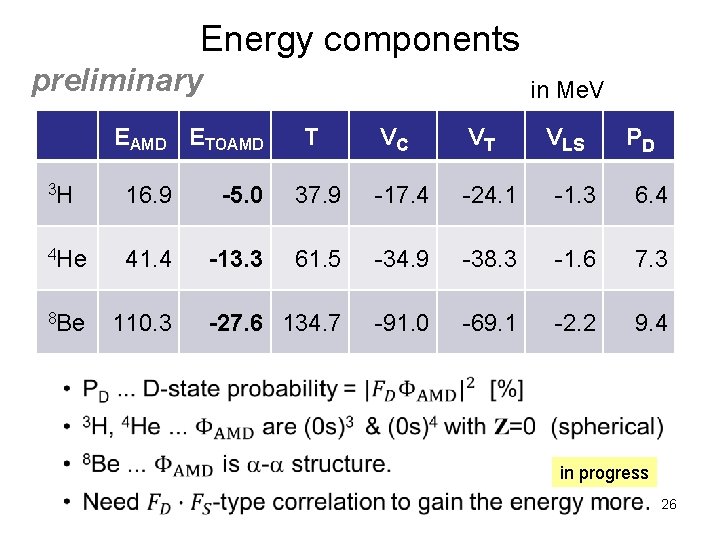
Energy components preliminary in Me. V EAMD ETOAMD T VC VT VLS PD 3 H 16. 9 -5. 0 37. 9 -17. 4 -24. 1 -1. 3 6. 4 4 He 41. 4 -13. 3 61. 5 -34. 9 -38. 3 -1. 6 7. 3 8 Be 110. 3 -27. 6 134. 7 -91. 0 -69. 1 -2. 2 9. 4 • in progress 26

Correlation functions FD, FS in 3 H FS 3 E 2 r 2 FD 3 E preliminary FS 1 E same trend in 3 H, 4 He, 8 Be • 27

Summary • Tensor-Optimized Shell Model (TOSM) using Vbare. – Strong tensor correlation from 0 p 0 h-2 p 2 h involving high-k components. – He, Li, Be isotopes : Energy spectra, Radius of n-rich nuclei. – For 8 Be, two aspects : grand state region & highly excited states, which indicates of more configurations, such as a-a states. • Tensor-Optimized AMD (TOAMD). – Two-kinds of correlation functions FD (tensor) & FS (short-range) – Three-body term contributes to the energy saturation. – Ranges of FD , FS are not short. – Spatially compact behavior of FD produces high-k component. 28