Strong Induction Normal Induction Induction If we prove

Strong Induction “Normal” Induction: Induction If we prove that 1) P(n 0) is true for some n 0 (typically 0 or 1), and 2) If P(k) is true for any k≥n 0, then P(k+1) is also true. Then P(n) is true for all n≥n 0. “Strong” Induction: Induction If we prove that 1) Q(n 0) is true for some n 0 (typically 0 or 1), and 2) If Q(j) is true for all j from n 0 to k (for any k≥n 0), then Q(k+1) is also true. Then Q(k) is true for all k≥n 0. These 2 forms are equivalent: Let P(n) = “n “ 0≤j≤n Q(j)” Ref: http: //en. wikipedia. org/wiki/Strong_induction UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 1

Proof by Strong Induction: Jigsaw Puzzle Each “step” in assembling a jigsaw puzzle consists of putting together 2 already assembled blocks of pieces where each single piece is considered a block itself. P(n) = “It takes exactly n-1 steps to assemble a jigsaw puzzle of n pieces. ” Basis Step: P(1) is (trivially) true. Inductive Step: We assume P(k) true for k≤n and we’ll argue P(n+1): The last step in assembling a puzzle with n+1 steps is to put together 2 blocks: one of size j>0 and one of size n+1 -j. By since 0<j, n+1 -j≤n, P(j) and P(n+1 -j) are both assumed true. And so, the total number of steps to assemble a puzzle with n+1 pieces is 1 + (j-1) + ((n+1 -j)-1) = n = (n+1)-1. (this implies P(n+1), and hence ends the inductive part, and thus also the whole proof) UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 2

More Examples of Theorems with easy Proofs using Strong Induction Thm 1: The second player always wins the following game: – Starting with 2 piles each containing the same number of matches, players alternately remove any non-zero number of matches from one of the piles. – The winner is the person who removes the last match. Thm 2: Every n>1 can be written as the product of primes. Thm 3: Every postage amount of at least 18 cents can be formed using just 4 -cent and 7 -cent stamps. UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 3

Basis for Induction: Integers are well ordered Induction is based on the fact that the integers are “well ordered” in the following sense: Any non-empty set of integers which is bounded below i. e. there exists b (not necessarily in S) s. t. b ≤ x for all x in S contains a least element i. e. element e in S s. t. for all x in S we have e ≤ x. Fact: The integers are well ordered. Why does well-ordering imply induction? Assume P(0) and P(k)→P(k+1) for all k≥ 0. We’ll show that P(n) is true for all n≥ 0 (thus showing that induction works): Define S = {n>0 | P(n) is not true}. Assume S non-empty. By well-ordering of N, there is a least element e of S. Let k=e-1≥ 0. If (not P(e)) then (not P(e-1)). We conclude that (not P(e-1)). e-1 cannot be equal to 0 because P(0) is true. But then e-1 must be in S, and so e is not the least element of S! => Contradiction => Therefore S must b empty. Therefore P(n) is true for all n>0. Since P(0) is also true, P(n) is true for all n≥ 0. UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 4

Well Ordering can be used directly to prove things (i. e. not necessarily via induction) Thrm: If a and b are integers, not both 0, then s, t Z (sa + tb = gcd(a, b)). Proof: For any a, b define S = {n>0 | s, t Z n= sa + tb}. By the well-ordering of Z, S has a smallest element, call it d. Choose s and t so that d = sa + tb. Claim: d is a common divisor of a and b. Proof that d|a: Writing d=qa+r where 0≤r<d. If r=0 then d|a. If r>0 then since r=d-qa=(sa+tb)-qa=(s-q)a+tb we would have r S. But since r<d it would mean that d is not the smallest element of S => contradiction => and therefore r=0 (and hence d|a). Similarly, d|b. d is the greatest common divisor since any common divisor of a and b must also divide sa+tb=d. UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 5

Recursive (Inductive) Definitions A function f: N→R is defined “recursively” by specifying (1) f(0), its value at 0, and (2) f(n), for n>0, in terms of f(1), …. , f(n-1), i. e. in terms of f(k)’s for k<n. Examples: – f(n)=n! can be specified as f(0)=1 and, for n>0, f(n)=n*f(n-1). – For any a, fa(n)=an, can be specified as fa(0)=1 and, for n>0, fa(n)=a*fa(n-1) Note: In many cases, we specify f(k) explicitly not only for f(0) but also for f(1), f(2), …, f(m) for some m>0, and then use a recursive formula to define f(n) for all n>m. UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 6

Fibonacci Numbers are Recursively Defined The Fibonacci numbers f 0, f 1, f 2, …, fn, …, are defined by (1) f 0=0, f 1=1 (2) fn=fn-1+fn-2, for n≥ 2 Subscripts can be a real pain and can interfere with understanding. It is often convenient to use F(n) instead of fn The Fibonacci numbers are f 0=0, f 1=1, f 2=1, f 3=2, f 4=3, f 5=5, f 6=8, f 7=13, f 8=21, f 9=34, f 10=55, f 10=89, f 11=144, f 12=233, f 13=377, f 14=610, f 15=987, f 11=1597, f 12=2584, f 13=4181, f 14=6765, f 15=10946, f 16=17711, f 17=28657, f 18=46368, . . . Ref: http: //en. wikipedia. org/wiki/Fibonacci_number UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 7

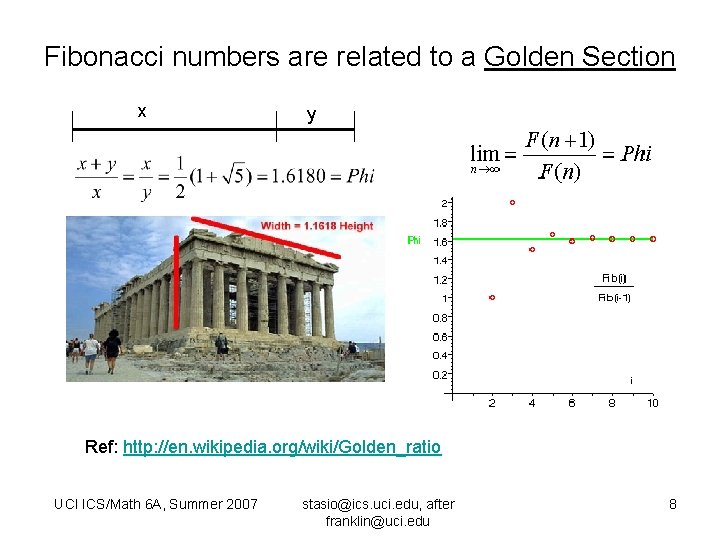
Fibonacci numbers are related to a Golden Section x y Ref: http: //en. wikipedia. org/wiki/Golden_ratio UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 8

Fibonacci Growth Theorem: Let φ=(1+ 5)/2 and n≥ 3 then fn > φ n-2 Proof by Strong Induction: Basis Step (for n=3 and 4): f 3 = 2 > φ =1. 618… f 4 = 3 > φ2 = (1+2 5+5)/4 = (3+ 5)/2 = φ+1 = 2. 168… (Note: Along the way, we showed that φ2 = φ+1) Inductive Step: Assume fk>φk-2 for all k s. t. 3≤k≤n. fn+1 = fn+fn-1 > φn-2+φn-3 = φn-3(φ+1) = φn-3φ2 = φ(n+1)-2 UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 9

Recursively Defined Sets Always (1) “Basis Step” and (2) “Recursive Step” Multiples of 3 (1) 3 S. (2) If x S and y S, then x+y S. Strings Σ* over an alphabet Σ. Let λ be the empty string. (1) λ Σ*. (2) If w Σ* and x Σ, then wx Σ*. Examples: Σ={0, 1}; Σ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; Σ={a, b, c, d, e, …, x, y, z} Now recursively define (“length”) L: Σ*→N by (1) L(λ)=0; (2)L(wx)=L(x)+1 L( String Catenation (“ • ”) (1) If w Σ*, then w • λ=w (2) If u, w Σ* and x Σ, then u • (wx)=(u • w)x UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 10

Recursively Defined Sets Always (1) “Basis Step” and (2) “Recursive Step” Well-Formed Boolean Formulae (1) T, F, and s, where s is a propositional variable are all well-formed Boolean formulae (WFBF). (2) If E and F are WFBF’s, then (¬E), (E F), and (E↔F) are all WFBF’s. Well-Formed Arithmetic Expressions (1) x is a well-formed arithmetic expression (WFAE) if x is a numeral or a variable. (2) If F and G are WFAE’s, then (F+G), (F-G), (F*G), (F/G), and (E F) are all WFAE’s. UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 11

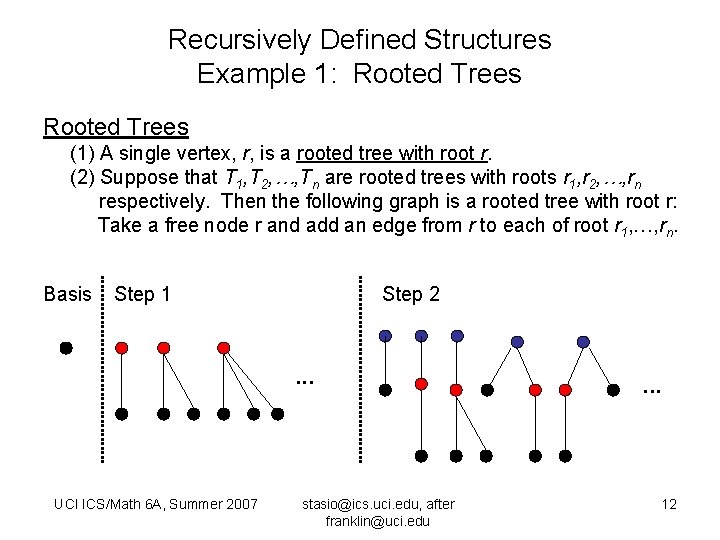
Recursively Defined Structures Example 1: Rooted Trees (1) A single vertex, r, is a rooted tree with root r. (2) Suppose that T 1, T 2, …, Tn are rooted trees with roots r 1, r 2, …, rn respectively. Then the following graph is a rooted tree with root r: Take a free node r and add an edge from r to each of root r 1, …, rn. Basis Step 1 Step 2 . . . UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu . . . 12

Recursively Defined Structures Example 2: Extended Binary Trees (1) The empty set is an Extended Binary Tree (EBT) (2) If T 1 and T 2 are EBT’s, then the following tree, denoted T 1 • T 2 , is also an EBT: Pick a new root, r, and attach T 1 as r’s left subtree and attach T 2 as r’s right subtree. - “Extended” means that even an empty set is considered a tree. - “Binary” means that every node has at most 2 children. Basis Step 1 Step 2 Step 3 One element: An Empty Set! UCI ICS/Math 6 A, Summer 2007 . . . stasio@ics. uci. edu, after franklin@uci. edu 13

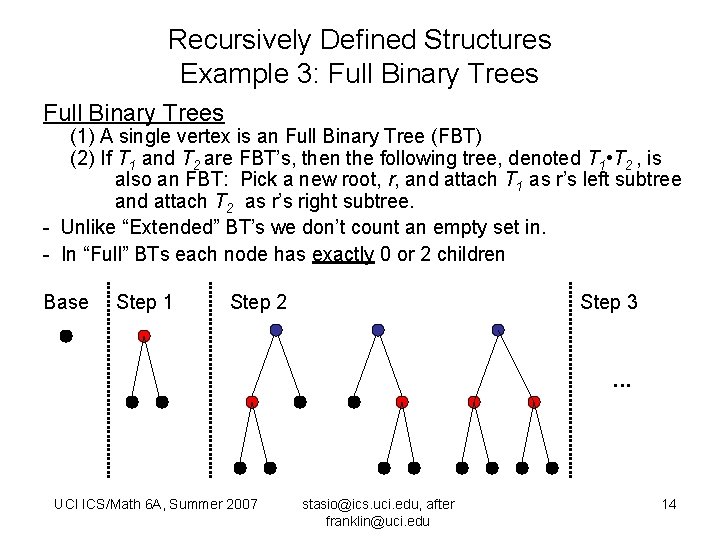
Recursively Defined Structures Example 3: Full Binary Trees (1) A single vertex is an Full Binary Tree (FBT) (2) If T 1 and T 2 are FBT’s, then the following tree, denoted T 1 • T 2 , is also an FBT: Pick a new root, r, and attach T 1 as r’s left subtree and attach T 2 as r’s right subtree. - Unlike “Extended” BT’s we don’t count an empty set in. - In “Full” BTs each node has exactly 0 or 2 children Base Step 1 Step 2 Step 3 . . . UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 14

Recursive Definitions of Functions on recursively defined objects (e. g. Full Binary Trees) Trees were defined recursively. Natural definition of a function on trees will be recursive as well! Examples: The Height function, h(T): (1) If T has a single (root) node/vertex, h(T)=0. (2) o/w, i. e. if T=T 1 • T 2, , then h(T) = h(T 1 • T 2 ) = 1+max(h(T 1), h(T 2 )) The Number of vertices (function), n(T): (1) If T has a single (root) node/vertex, n(T)=1. (2) o/w, i. e. if T=T 1 • T 2, , then n(T) = n(T 1 • T 2 ) = 1+n(T 1)+n(T 2 ) UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 15

Structural Induction If a set is recursively defined, to show a result true for all elements in the set: (1) Show the result is true for all elements the basis step includes. (2) Show that if the result is true for each of the elements used to construct a new element, it is also true for that new element. Thrm: If T is a full binary tree, then n(T)≤ 2 h(T)+1 -1 (proof on next slide) Ref: http: //en. wikipedia. org/wiki/Structural_induction UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 16

Structural Induction Example Thrm: If T is a full binary tree, then n(T)≤ 2 h(T)+1 -1 Proof: Basis Step: If T is just the root vertex, n(T)=1, h(T)=0 and n(T)=1≤ 1=20+1 -1 Inductive Step: When T= T 1 • T 2 , we compute n(T)=1+n(T 1)+n(T 2) ≤ 1+(2 h(T 1)+1 -1)+(2 h(T 2)+1 -1) ≤ 2·max(2 h(T 1)+1, 2 h(T 2)+1)-1 Definition of n(T) Induction hypothesis Arithmetic = 2· 21+max(h(T 1), h(T 2)) -1 Arithmetic = 2· 2 h(T)-1 Definition of h(T) UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 17

Recursive Algorithms An algorithm is “recursive” if it solves a problem by reducing it to an instance of the same problem with smaller input. Examples: 1. procedure factorial (n: nonnegative integer) if n=0 then factorial(n) : = 1 else factorial(n) : = n ·factorial(n-1) 2. procedure power(a: nonzero real, n: nonnegative integer) if n=0 then power(a, n) : = 1 else power(a, n) : = a·power(a, n-1) 3. procedure gcd(a, b: nonnegative integers with a<b) if a=0 then gcd(a, b) : = b else gcd(a, b) : = gcd(b mod a, a) 4. procedure fibonacci (n: nonnegative integer) if n≤ 1 then fibonacci(n) : = 1 else fibonacci(n) : = fibonacci(n-1) + fibonacci(n-2) UCI ICS/Math 6 A, Summer 2007 stasio@ics. uci. edu, after franklin@uci. edu 18