Strong AcidWeak Base and Weak Acid Strong Base
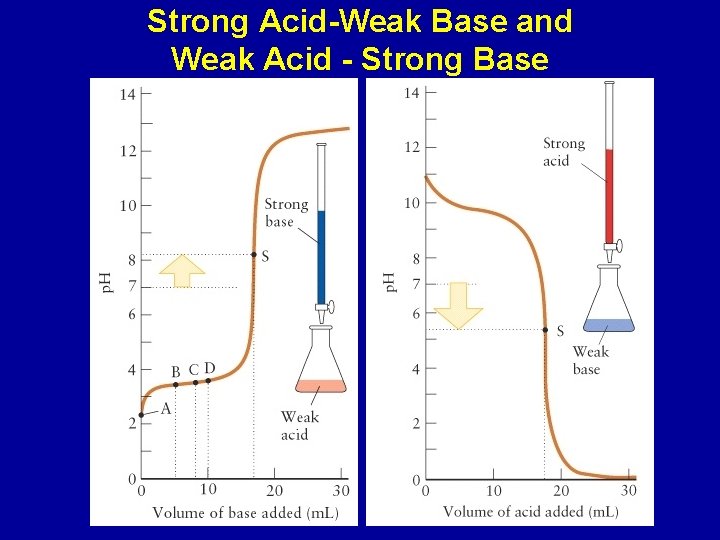
Strong Acid-Weak Base and Weak Acid - Strong Base
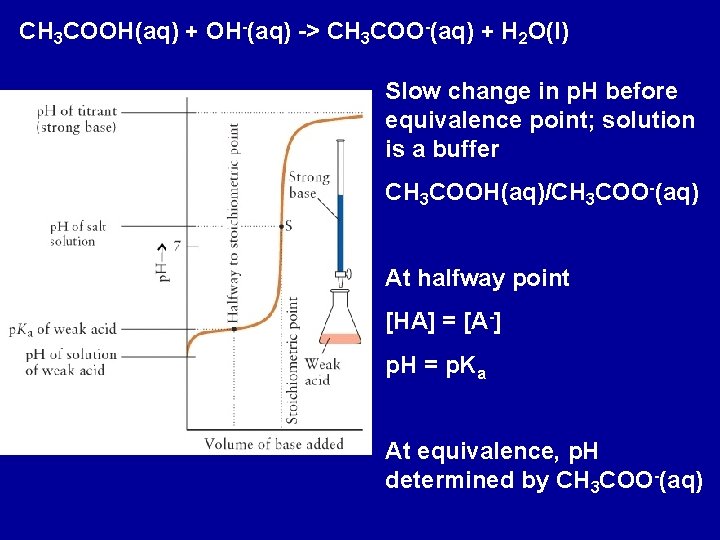
CH 3 COOH(aq) + OH-(aq) -> CH 3 COO-(aq) + H 2 O(l) Slow change in p. H before equivalence point; solution is a buffer CH 3 COOH(aq)/CH 3 COO-(aq) At halfway point [HA] = [A-] p. H = p. Ka At equivalence, p. H determined by CH 3 COO-(aq)

Changes in p. H during a titration of a weak acid/base with a strong base/acid: Halfway to the stoichiometric point, the p. H = p. Ka of the acid The p. H is greater than 7 at the equivalence point of the titration of a weak acid and strong base The p. H is less that 7 at the equivalence point of the titration of a weak base and strong acid Beyond the equivalence point, the excess strong acid or base will determine the p. H of the solution

Titration of 100. 0 m. L of 0. 1000 M CH 3 COOH(aq) with 0. 1000 M Na. OH Before addition of Na. OH: p. H determined by CH 3 COOH(aq) + H 2 O(l) H 3 O+(aq) + CH 3 COO-(aq) Answer: p. H = 2. 88 Before the equivalence point: determine p. H for a buffer Addition of 30. 00 m. L of Na. OH(aq) The OH-(aq) reacts with the CH 3 COOH(aq). Determine concentration of CH 3 COOH(aq) and CH 3 COO- (aq) in solution after addition of the base. Answer: p. H = 4. 38 At half equivalence: [CH 3 COOH(aq)] = [CH 3 COO-(aq)] p. H = p. Ka

At equivalence: enough OH-(aq) added to react with all CH 3 COOH(aq). For this problem, equivalence is reached when 100. 0 m. L of OH- is added; i. e. 0. 01000 moles of OH-(aq) added Solution contains 0. 01000 moles CH 3 COO-(aq) in 200. 0 m. L solution; [CH 3 COO-(aq)] = 0. 05000 M p. H determined by CH 3 COO-(aq) + H 2 O(l) CH 3 COOH(aq) + OH- (aq) p. H = 8. 72 (note greater than 7. 0) Beyond equivalence: p. H determined by excess OH-(aq)

Estimate the p. H at the equivalence point of the titration of 25. 00 m. L of 0. 100 M HCOOH(aq) with 0. 150 M Na. OH(aq) (Ka(HCOOH) = 1. 8 x 10 -4) At the equivalence point, enough Na. OH(aq) has been added to react with all the HCOOH(aq) forming HCOO-(aq) The reaction: HCOO-(aq) + H 2 O(l) HCOOH(aq) + OHdetermines the p. H at equivalence Answer: 8. 26
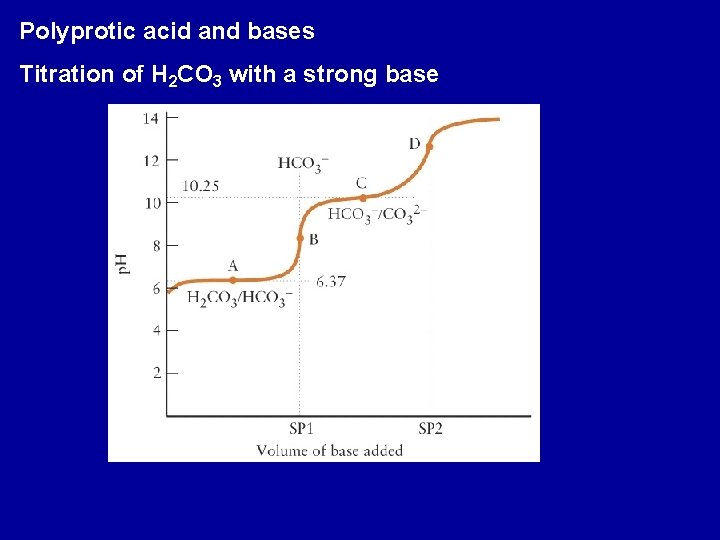
Polyprotic acid and bases Titration of H 2 CO 3 with a strong base
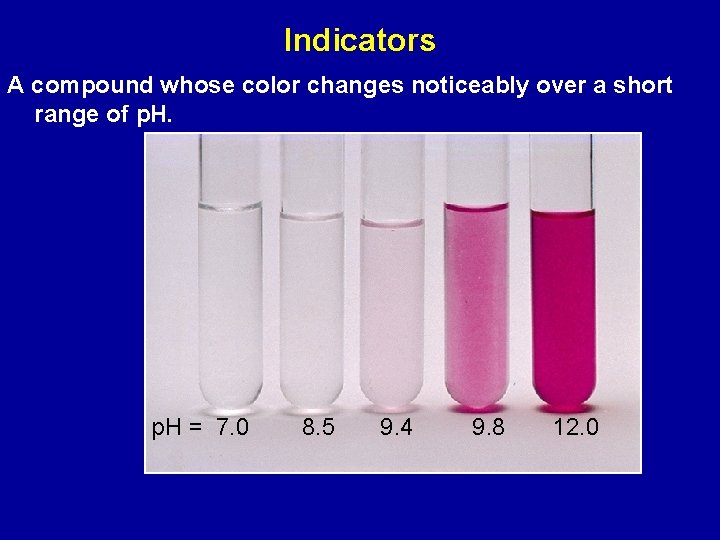
Indicators A compound whose color changes noticeably over a short range of p. H = 7. 0 8. 5 9. 4 9. 8 12. 0
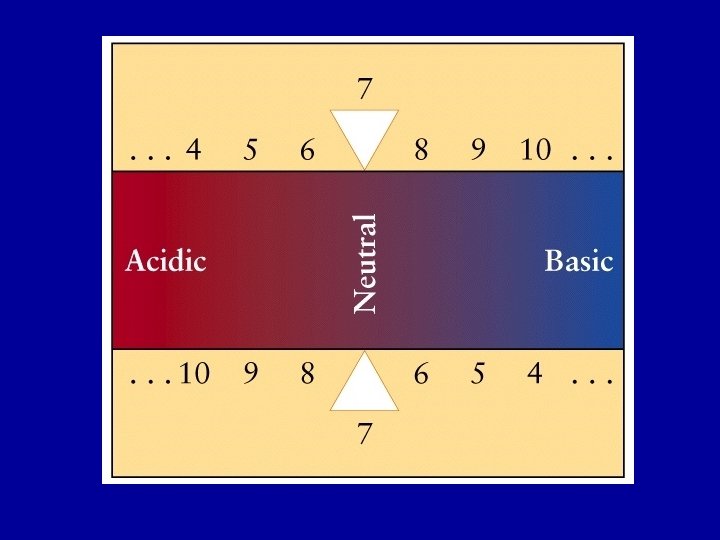

The indicator is a weak acid itself (HIn) HIn(aq) + H 2 O(l) In- (aq) + H 3 O+ (aq) KIn = [In- (aq)] [H 3 O+(aq)] [HIn (aq) ] The acid form, HIn, has a different color from the base form In - The end point of a titration is the point at which the concentrations of the acid and base forms of the indicator are equal; [HIn(aq)] = [In-(aq)] Color change occurs when p. H = p. KIn
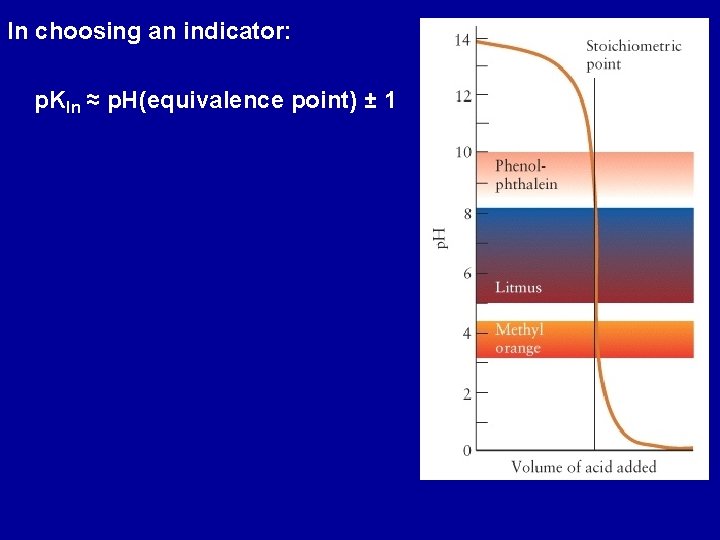
In choosing an indicator: p. KIn ≈ p. H(equivalence point) ± 1

Applications Atmospheric CO 2(g) + H 2 O(l) H 2 CO 3(aq) + H 2 O(l) HCO 3 -(aq) + H 3 O+(aq) Acid rain: When p. H < 5. 5 due to pollutants in the air like SO 2, SO 3, NO 2, which dissolve in water to form strong acids Many lakes have water too acidic to sustain life, forests have also been damaged. In the ground, acidic rain water can be neutralized by ions in the soil

The ocean is buffered to a p. H of 8. 4 by buffering that depends on the presence of hydrogen carbonates and silicates Physiological Buffers: Body fluids such as blood function over a very narrow p. H range, maintained by buffers Blood contains two buffering systems: 1) Phosphate buffer (H 2 PO 4 -/HPO 42 -) H 2 PO 4 -(aq) + H 2 O(l) H 3 O+(aq) + HPO 42 -(aq) Ka 2 = 6. 2 x 10 -8, p. Ka 2 = 7. 21 Average p. H of blood is 7. 40 indicates that [HPO 42 -(aq)] / [H 2 PO 4 -(aq) ] = 1. 55

2) HCO 3 -/H 2 CO 3 buffer CO 2(g) + H 2 O(l) H 2 CO 3(aq) + H 2 O(l) HCO 3 -(aq) + H 3 O+(aq) p. Ka 1 = 6. 36 [HCO 3 -(aq)] / [H 2 CO 3(aq) ] = 11. 0 Build up of H 2 CO 3 would destroy this balance. In the body H 2 CO 3(aq) H 2 O(l) + CO 2 (g) CO 2 is exhaled from the lungs to prevent buildup of H 2 CO 3

Solubility Equilibria Many ionic solids dissociate into their ions in water: Na. Cl(aq) -> Na+(aq) + Cl- (aq). Compounds such as Na. Cl exist completely as Na+ (aq) and Cl(aq) in aqueous solutions unless the amount of Na. Cl exceeds the solubility of Na. Cl in water Other compounds such as Ca. CO 3 dissolve to a very small extent in water - sparingly soluble

The Earth’s crust consists largely of sparingly soluble salts; e. g. gypsum (Ca. SO 4. 2 H 2 O), calcite �(Ca. CO 3), dolomite (x. Ca. CO 3. y. Mg. CO 3), oxides and sulfides of metals such as Fe, aluminosilicates (XAl. Si 3 O 8 or XAl. Si 2 O 8, X = Na+, K+, Ca 2+) Hard-water contains high levels of Ca 2+ and Mg 2+ Ca 2+ forms soap scum with detergents. Add soluble Na 2 CO 3 (washing soda) to precipitate Ca. CO 3 which washes off. Chemical weathering includes the dissolving of sparingly soluble salts. Ca. CO 3(s) + CO 2(g) + H 2 O(l) Ca 2+(aq) + 2 HCO 3 -(aq)

Highly soluble compounds: several grams of the compound dissolves per 100 g of water At 298 K: 36 g of Na. Cl, 122 g of Ag. NO 3 Sparingly soluble compounds: less than one gram dissolves per 100 g of water At 298 K: 2. 4 x 10 -4 g of Ag. Cl; 9. 3 x 10 -4 g of Ca. CO 3, 4. 4 x 10 -14 g of Pb. S

Ag. Cl(s) Ag+ (aq) + Cl- (aq) Define an equilibrium constant for this process: solubility product, Ksp = [Ag+ (aq)] [Cl- (aq)] The solubility product, Ksp, is the equilibrium constant for the equilibrium between an undissolved salt and its ions in a saturated solution.
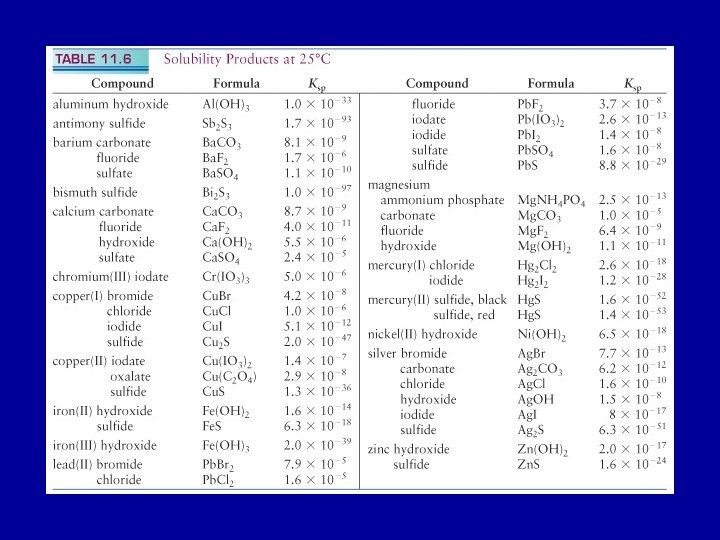

The molar solubility of Ag 2 Cr 2 O 4 is 6. 5 x 10 -5 mol/L at 25 o C. Determine the value of Ksp. Ag 2 Cr 2 O 4(s) 2 Ag+ (aq) + Cr 2 O 42 - (aq) Ksp = [Ag+ (aq) ]2 [Cr 2 O 42 - (aq)] [Ag+ (aq) ] = 2 x 6. 5 x 10 -5 mol/L [Cr 2 O 42 - (aq) ] = 6. 5 x 10 -5 mol/L Ksp = 1. 1 x 10 -12

Determine the solubility of Ba. SO 4(s) in pure water at 298 K in moles/liter and grams/liter. Ksp (Ba. SO 4) = 1. 1 x 10 -10 Ba. SO 4(s) Ba 2+ (aq) + SO 42 - (aq) If x is the solubility in moles/liter [Ba 2+(aq)] [SO 42 -(aq)] = x 2 = 1. 1 x 10 -10 [Ba 2+(aq)] = [SO 42 -(aq)] = 1. 0 x 10 -5 M Solubility of Ba. SO 4 is 1. 0 x 10 -5 M or 2. 3 x 10 -3 g/L

Precipitation from Solution If equal volumes of aqueous solutions of 0. 2 M Pb(NO 3)2 and KI are mixed will Pb. I 2(s) precipitate out? Ksp of Pb. I 2 is 1. 4 x 10 -8 Use the reaction quotient, Q, to predict whether precipitation will occur Pb(NO 3)2 (aq) + KI(aq) -> Pb. I 2 (s) + KNO 3 (aq) Net ionic equation: Pb 2+ (aq) + 2 I- (aq) -> Pb. I 2 (s) The reverse of this reaction defines Ksp Pb. I 2 (s) Pb 2+ (aq) + 2 I- (aq)
![Ksp = [Pb 2+ (aq)] [I- (aq)]2 If Q > Ksp precipitation; if Q Ksp = [Pb 2+ (aq)] [I- (aq)]2 If Q > Ksp precipitation; if Q](http://slidetodoc.com/presentation_image_h/1265af5c8f9022d63d2b8e141ab1649d/image-23.jpg)
Ksp = [Pb 2+ (aq)] [I- (aq)]2 If Q > Ksp precipitation; if Q < Ksp no precipitation Equal volumes of Pb(NO 3)2 and KI are mixed On mixing, volume of mixed solution is twice initial volume [Pb 2+ (aq)] = 0. 2 M / 2 = 0. 1 M [I- (aq)] = 0. 1 M Q = [Pb 2+(aq)] [I- (aq)]2 = (0. 1)2 = 0. 001 M Q > Ksp; Pb. I 2(s) precipitates
- Slides: 23