STRINGS AND AUTOMATA MODULO THEORIES Margus Veanes July

STRINGS AND AUTOMATA MODULO THEORIES Margus Veanes July 18, 2015 SMT'15, San Fransisco 1

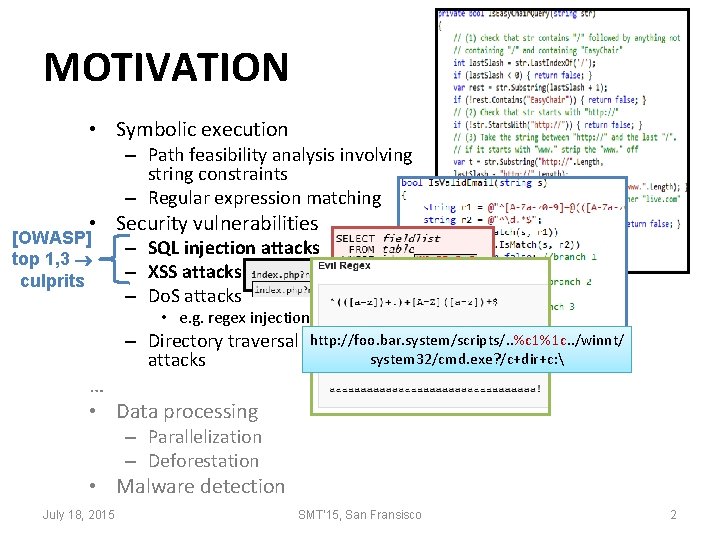
MOTIVATION • Symbolic execution – Path feasibility analysis involving string constraints – Regular expression matching • Security vulnerabilities [OWASP] top 1, 3 culprits – SQL injection attacks – XSS attacks – Do. S attacks • e. g. regex injection – Directory traversal attacks http: //foo. bar. system/scripts/. . %c 1%1 c. . /winnt/ system 32/cmd. exe? /c+dir+c: … • Data processing – Parallelization – Deforestation • Malware detection July 18, 2015 SMT'15, San Fransisco 2

“EARLY” WORK RELATED TO STRING ANALYSIS • Tools – Mona: Henriksen-Jensen-Jørgensen-Klarlund-Paige-Rauhe-Sandholm, TACAS’ 95 • Built on BRICS automata library – JSA: Christensen-Møller-Schwartzbach, SAS’ 03 (Uses BRICS) – Haderach: Shannon-Hajra-Lee-Zhan-Khurshid, MUTATION’ 07 (Uses BRICS) • Theory – – – Bjørner, Ph. D Thesis’ 98, Decision procedure for queues Blumensath-Grädel, LICS’ 00 (automatic structures) Benedikt-Libkin-Schwentick-Segoufin, LICS’ 01 (regular string relations) Khoussainov-Nies-Rubin-Stephan, LICS’ 04 (automatic Boolean Algebras) Bala, STACS’ 04, (regular term matching) Kunc, DLT’ 2007, (complexity of language equations) July 18, 2015 SMT'15, San Fransisco 3

THE RISE OF THE STRING ANALYZERS • String theory encodings in SMT: – – – • Pex-LL: Bjørner-Tillmann-Voronkov, TACAS’ 09 Reggae: Li-Xie-Tillmann-de. Halleux-Schulte, ASE’ 09 Z 3 -str: Zheng-Zhang-Ganesh, ESEC/FSE 2013 CVC 4 -str: Liang-Reynolds-Tinelli-Barrett-Deters, CAV’ 14 S 3: Trinh-Chu-Jaffar, CCS’ 14 Automata related: – – – – – CAV’ 15: – – – July 18, 2015 (strings + SMT) (symolic exploration of regex code) (plugin to Z 3) (DPLL(TSLRp)) (uses Z 3 -str-star) Stranger: Yu-Alkhalaf-Bultan-Ibarra-Cova, SPIN’ 08, TACAS’ 09, TACAS’ 10 (automata based) DPRLE: Hooimeijer-Weimer, PLDI’ 09 (subset checking) Hampi: Kiezun-Ganesh-Guo-Hooimeijer-Ernst, ISSTA’ 09 (best paper award) (reduction to BV) Kaluza(in Kudzu): Saxena-Akhawe-Hanna-Mao-Mc. Camant-Song, Okland’ 10 (Hampi + mult. var. ) Rex: Veanes-de. Halleux-Tillmann-Bjørner-de. Moura, ICST’ 10, LPAR’ 2010 (language acceptors) Bek: Hooimeijer-Livshits-Molnar-Saxena-Veanes-Bjørner, USENIX Security'11, POPL’ 12 (transducers) Bex: D’Antoni-Veanes, VMCAI’ 13, CAV’ 13 (lookahead) PASS: Li-Ghosh, HVC 2013 (best paper award). (array based) SMC: Luu-Shinde-Saxena-Demsky, PLDI’ 14 (model counting) ABC: Aydin-Bang-Bultan (automata based counting, using Stranger and BRICS) NORN: Abdulla-Atig-Chen-Holik-Rezine-Rümmer-Stenman, also CAV’ 14 (Horn clauses, BRICS) + Z 3 -str : Zheng-Ganesh-Subramanian-Tripp-Dolby-Zhang. (string + regex + length ) SMT'15, San Fransisco 4

TWO QUESTIONS Is this a string function? • What are characters? • What are strings? smileycipher(“hello world”) = “����� ” July 18, 2015 SMT'15, San Fransisco 5

WHAT ARE CHARACTERS? 1. Elements of a Finite Alphabet ? – Only primitive operation is =: Bool – What about Unicode, e. g. , �� http: //unicode. org/charts/PDF/U 1 F 600. pdf • | | = 1, 112, 064 – For succinctness allow total order ≺: Bool and ranges [a-b] (denotes {x | a ≼ x ≼ b}) • This affects the notion of automaton over ! • Why not other operations as well? 2. Bit-vectors, say char (BV 16) ? – With primitive operations like &: char – “�� ” = “u. D 83 Du. DE 00” (UTF 16 surrogate pair) • has its own theory, namely bv theory! 3. Integers (code points) ? – �� = 0 x 1 F 600 = 128512 – e. g. �� + 1 = �� = 0 x 1 F 601 … July 18, 2015 • has its own theory, namely int theory! SMT'15, San Fransisco 6

WHAT ARE STRINGS? • Finite sequences of characters (char) – CVC 4 -str Singleton string = char • Restricted arrays of int to char – Pex-LL, PASS array<int, char> ≠ char singleton string ≠ char • Finite lists of characters – Pex-Rex list<char> ≠ char singleton string ≠ char • Finite queues – transducers The answer depends on the context and the required operations. – First, Last, Rest, Append, Substring, Length, … July 18, 2015 SMT'15, San Fransisco 7

ANALYSIS TASKS • Consider character type C, string type S<C>, and regular expression type R<C>. – When is DPLL(TC, TS<C>, TR<C>) possible/feasible? • What about (finite state) transducers? – Regular transformations of type S<Tin> S<Tout> – Typically Tin = Tout = bit-vectors – Many string transformations are such: • sanitizers, encoders July 18, 2015 SMT'15, San Fransisco 8

HTML ENCODER Arithmetic operations on characters July 18, 2015 SMT'15, San Fransisco 9

FOR EACH DOMAIN SPECIFIC TASK Design a language that • only has the features required by the task • it is simple to use • enables to automatically reason about what the programs do • compiles into efficient code July 18, 2015 SMT'15, San Fransisco 10

THE REST OF THE TALK • • Symbolic Automata and Transducers BEK and string sanitizers BEX and string encoders Data parallel BEK/BEX for string processing July 18, 2015 SMT'15, San Fransisco 11

SYMBOLIC FINITE AUTOMATA July 18, 2015 SMT'15, San Fransisco 12

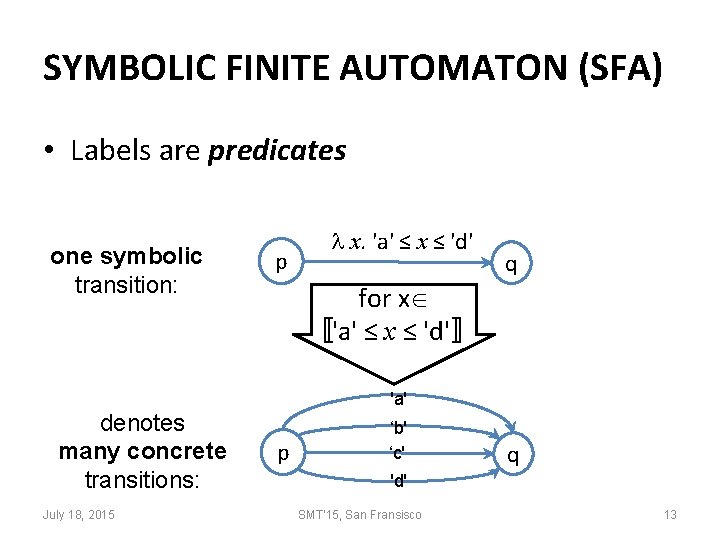
SYMBOLIC FINITE AUTOMATON (SFA) • Labels are predicates one symbolic transition: denotes many concrete transitions: July 18, 2015 p x. 'a' ≤ x ≤ 'd' q for x 〚'a' ≤ x ≤ 'd'〛 'a' p ‘b' ‘c' q 'd' SMT'15, San Fransisco 13

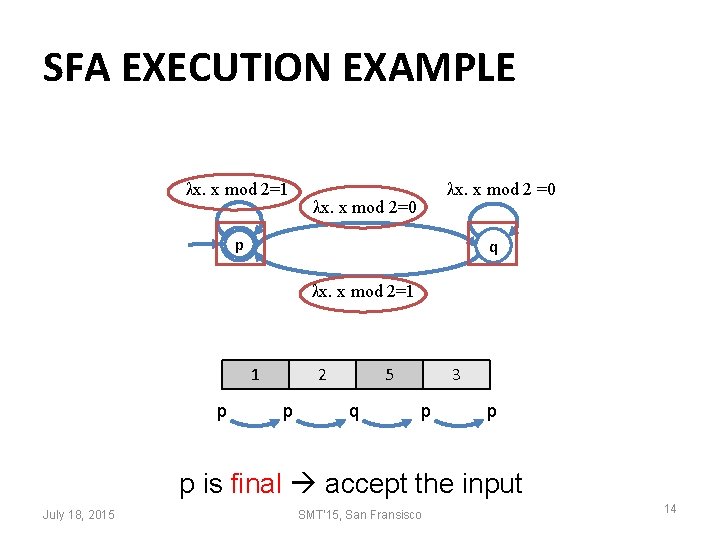
SFA EXECUTION EXAMPLE λx. x mod 2=1 λx. x mod 2 =0 λx. x mod 2=0 p q λx. x mod 2=1 1 p 2 p 5 q 3 p p p is final accept the input July 18, 2015 SMT'15, San Fransisco 14

SYMBOLIC FINITE AUTOMATA What is the alphabet? July 18, 2015 SMT'15, San Fransisco 15

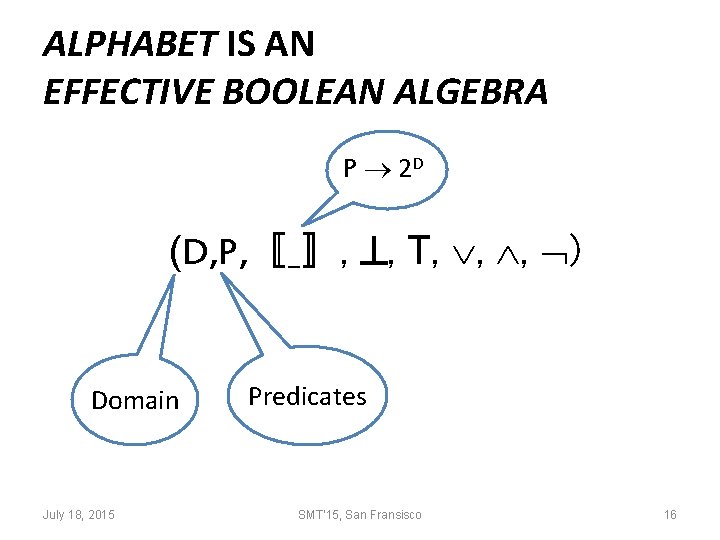
ALPHABET IS AN EFFECTIVE BOOLEAN ALGEBRA P 2 D (D, P, 〚_〛, , T, , , ) Domain July 18, 2015 Predicates SMT'15, San Fransisco 16

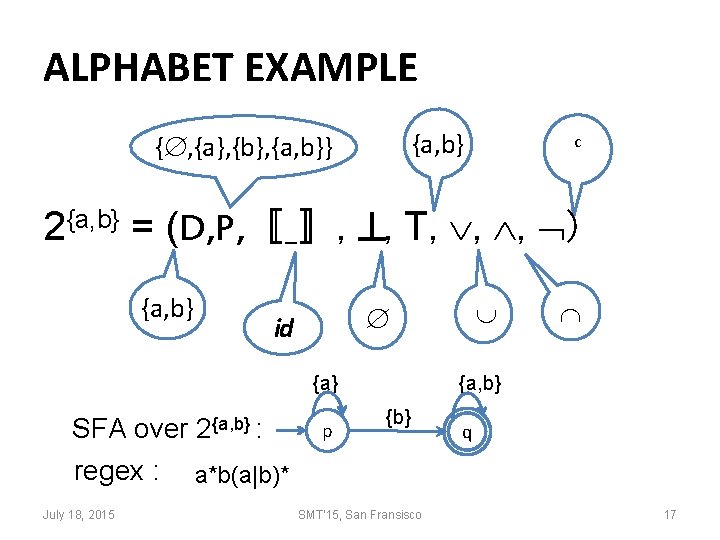
ALPHABET EXAMPLE {a, b} { , {a}, {b}, {a, b}} c 2{a, b} = (D, P, 〚_〛, , T, , , ) {a, b} id {a} SFA over 2{a, b} : regex : a*b(a|b)* July 18, 2015 p {a, b} {b} SMT'15, San Fransisco q 17

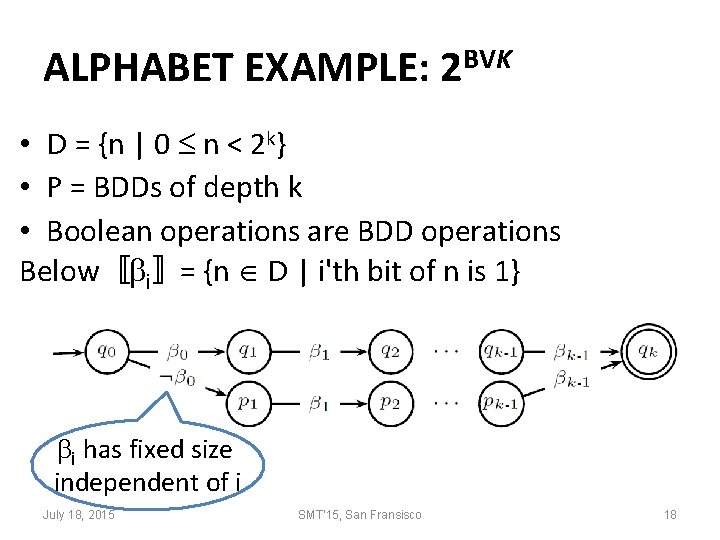
ALPHABET EXAMPLE: 2 BVK • D = {n | 0 n < 2 k} • P = BDDs of depth k • Boolean operations are BDD operations Below〚 i〛= {n D | i'th bit of n is 1} i has fixed size independent of i July 18, 2015 SMT'15, San Fransisco 18

ALPHABET EXAMPLE: SMTINT • D = Integers • P = integer linear arithmetic formulas (with one fixed free variable) • 〚 〛= 〚 〛 • 〚 〛= , 〚 〛= D 〚 〛 • Satisfiability: 〚 〛 July 18, 2015 SMT'15, San Fransisco 19

BOOLEAN ALGEBRA INTERFACE IN C# public interface IBool. Alg<P> { P Top { get; } P Bot { get; } P Not(P pred); P Or(P pred 1, P pred 2); P And(P pred 1, P pred 2); bool Is. Sat(P predicate); } public interface IBool. Alg. Ext<P, D> : IBool. Alg<P> { IEnumerable<D> Den(P); P One(D); } July 18, 2015 SMT'15, San Fransisco 20

UNIT ALPHABET EXAMPLE IN C# One-letter alphabet class A 1 : IBool. Alg<bool> { public bool Top { get { return true; } } public bool Bot { get { return false; } } public bool Not(bool pred) { return !pred; } public bool Or(bool pred 1, bool pred 2) { return pred 1 || pred 2; } public bool And(bool pred 1, bool pred 2) { return pred 1 && pred 2; } public bool Is. Sat(bool pred){ return pred; } } July 18, 2015 SMT'15, San Fransisco 21

ANOTHER ALPHABET EXAMPLE IN C# 16 -letter alphabet class A 16 : IBool. Alg<UInt 16> { public UInt 16 Top { get { return 0 x. FFFF; } } public UInt 16 Bot { get { return 0; } } public UInt 16 Not(UInt 16 pred) { return ~pred; } public UInt 16 Or(UInt 16 pred 1, UInt 16 pred 2) { return pred 1 | pred 2; } public UInt 16 And(UInt 16 pred 1, UInt 16 pred 2) { return pred 1 & pred 2; } public bool Is. Sat(UInt 16 pred){ return pred != 0; } } July 18, 2015 SMT'15, San Fransisco 22

ALPHABET TRANSFORMATIONS • Effective Boolean algebras can be extended – e. g. disjoint union • Effective Boolean algebras can be restricted – e. g. restriction wrt. a given predicate July 18, 2015 SMT'15, San Fransisco 23

DISJOINT UNION OF ALPHABETS IN C# public class Pair. Alg<S, T> : IBool. Alg<Pair<S, T>> { IBool. Alg<S> A; IBool. Alg<T> B; Pair<S, T> Bot {get return new Pair<S, T>(A. Bot, B. Bot); } … public Pair<S, T> Or(Pair<S, T> a, Pair<S, T> b) { return new Pair<S, T>(A. Or(a[0], b[0]), B. Or(a[1], b[1])); } public bool Is. Sat(Pair<S, T> p) { return A. Is. Sat(p[0]) || B. Is. Sat(p[1]); } } July 18, 2015 SMT'15, San Fransisco 24

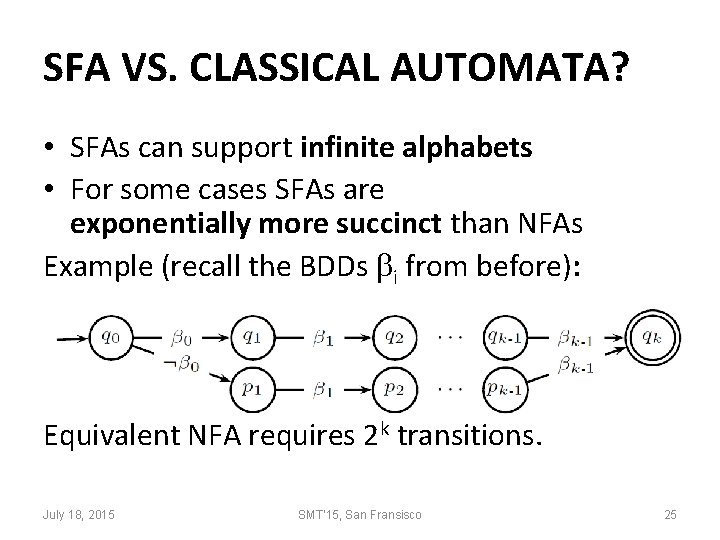
SFA VS. CLASSICAL AUTOMATA? • SFAs can support infinite alphabets • For some cases SFAs are exponentially more succinct than NFAs Example (recall the BDDs i from before): Equivalent NFA requires 2 k transitions. July 18, 2015 SMT'15, San Fransisco 25

SYMBOLIC FINITE AUTOMATA Algorithms over SFAs. July 18, 2015 SMT'15, San Fransisco 26

ALGORITHMS OVER SFAS • Language intersection – Uses product of automata • Language complementation – Requires determinization • Minimization – Extensions of Moore/Hopcroft [POPL’ 14] • Regex SFA construction – Uses BDDs to represent Unicode character sets – Requires BDD interval-set conversions • May cause exponential blowup: recall the BDDs i July 18, 2015 SMT'15, San Fransisco 27

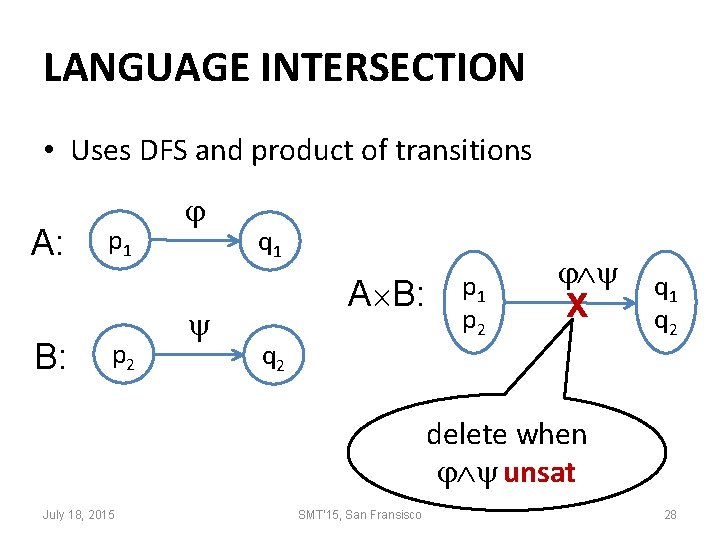
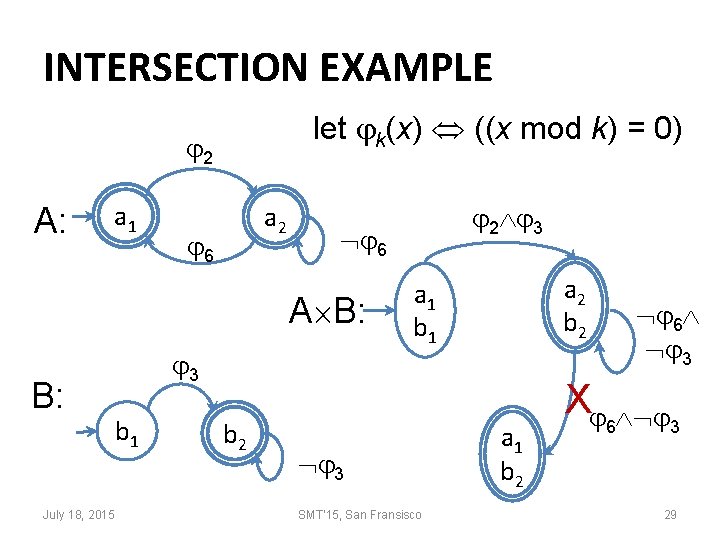
LANGUAGE INTERSECTION • Uses DFS and product of transitions A: B: p 1 p 2 q 1 A B: q 2 p 1 p 2 X q 1 q 2 delete when unsat July 18, 2015 SMT'15, San Fransisco 28

INTERSECTION EXAMPLE let k(x) ((x mod k) = 0) 2 A: a 1 a 2 6 6 A B: B: July 18, 2015 3 b 1 b 2 2 3 a 2 b 2 a 1 b 1 3 SMT'15, San Fransisco a 1 b 2 6 3 X 6 3 29

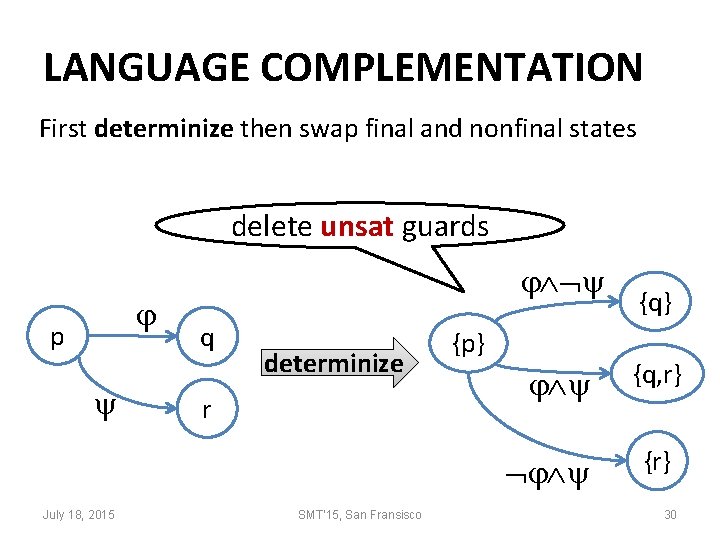
LANGUAGE COMPLEMENTATION First determinize then swap final and nonfinal states delete unsat guards p q determinize r {p} July 18, 2015 SMT'15, San Fransisco {q} {q, r} {r} 30

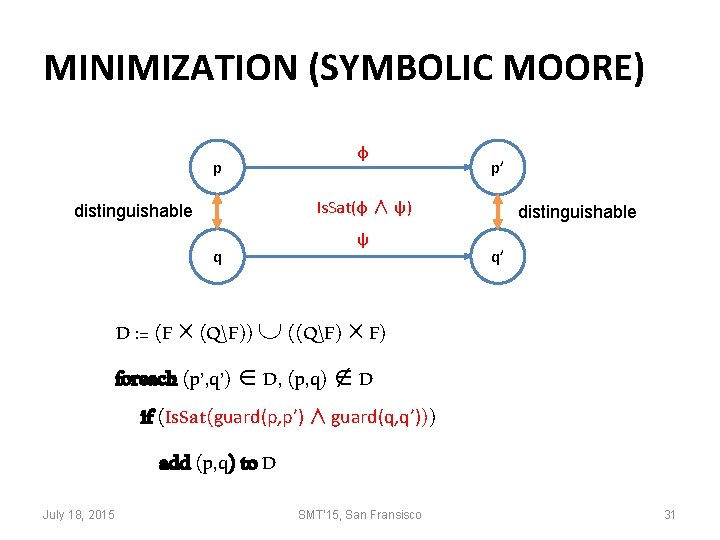
MINIMIZATION (SYMBOLIC MOORE) p φ p’ Is. Sat(φ ∧ ψ) distinguishable q ψ distinguishable q’ D : = (F (QF)) ((QF) F) foreach (p’, q’) D, (p, q) D if (Is. Sat(guard(p, p’) ∧ guard(q, q’))) add (p, q) to D July 18, 2015 SMT'15, San Fransisco 31

REGEX SFA • Classical algorithm extended to work with predicates – First produces SFA (SFA with -moves ) – Then -moves are eliminated using the standard -elimination algorithm – Requires interval-set BDD algorithm for converting character classes Example: [ x 0 - x. FF] = BDD whose bits in pos. > 7 are 0 July 18, 2015 SMT'15, San Fransisco 32

ONLINE SFA ALGORITHM EXAMPLES • http: //www. rise 4 fun. com/Bex/z. E July 18, 2015 SMT'15, San Fransisco 33

SYMBOLIC FINITE TRANSDUCERS July 18, 2015 SMT'15, San Fransisco 34

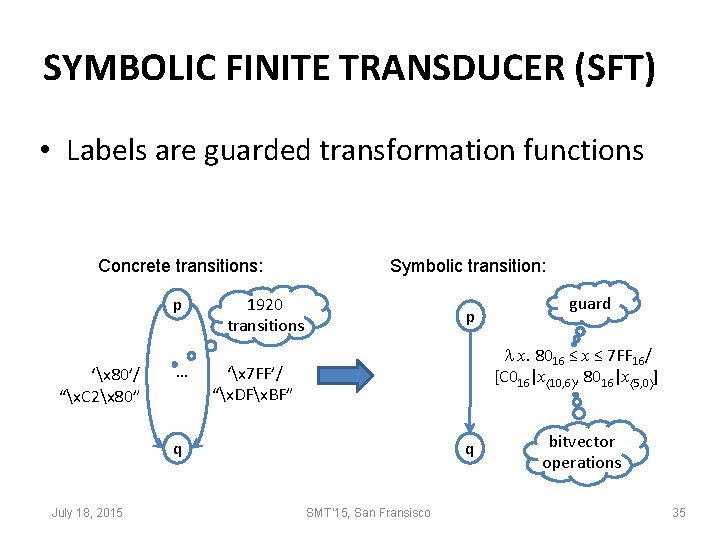
SYMBOLIC FINITE TRANSDUCER (SFT) • Labels are guarded transformation functions Concrete transitions: p ‘x 80’/ “x. C 2x 80” … Symbolic transition: 1920 transitions p x. 8016 ≤ x ≤ 7 FF 16/ [C 016|x 10, 6 , 8016|x 5, 0 ] ‘x 7 FF’/ “x. DFx. BF” q July 18, 2015 guard q SMT'15, San Fransisco bitvector operations 35

SFT EXECUTION EXAMPLE x mod 2 =1/[x-1] x mod 2 =0/[x, x] x mod 2 =0/[] p q x mod 2 =1/[x-1] Input tape 1 p Output tape July 18, 2015 2 p 0 5 q 2 3 p 2 SMT'15, San Fransisco p 4 2 36

SYMBOLIC FINITE TRANSDUCERS Properties and algorithms July 18, 2015 SMT'15, San Fransisco 37

WHY SFTS? • They have good algebraic properties (POPL'12) – SFTs are closed under composition – Equivalence is decidable in the single-valued case – domain of an SFT is an SFA • SFAs are closed under Boolean operations • Useful for various analysis tasks July 18, 2015 SMT'15, San Fransisco 38

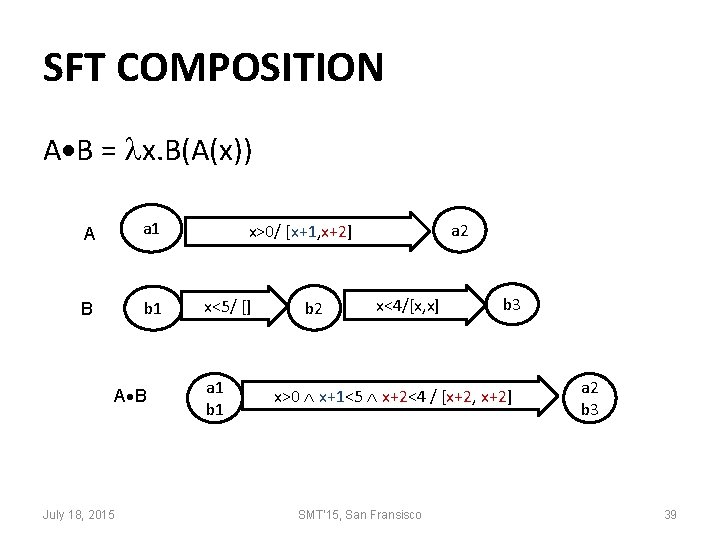
SFT COMPOSITION A B = x. B(A(x)) A a 1 B b 1 A B July 18, 2015 a 2 x>0/ [x+1, x+2] x<5/ [] a 1 b 2 x<4/[x, x] b 3 x>0 x+1<5 x+2<4 / [x+2, x+2] SMT'15, San Fransisco a 2 b 3 39

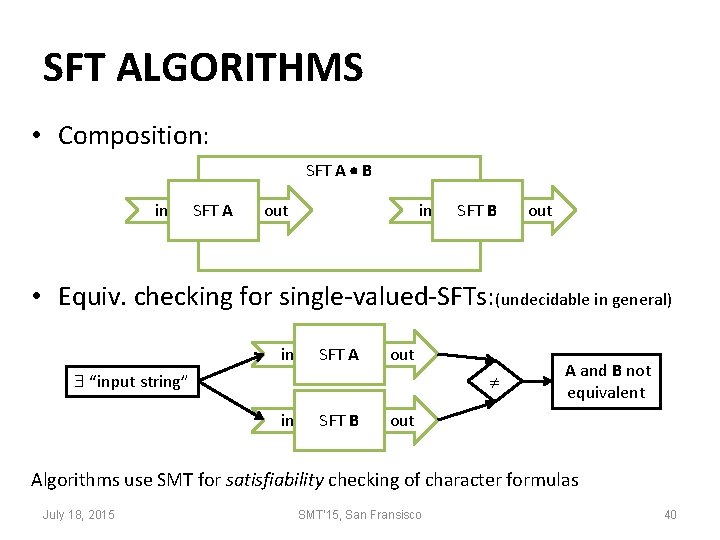
SFT ALGORITHMS • Composition: SFT A B in SFT A out in SFT B out • Equiv. checking for single-valued-SFTs: (undecidable in general) in SFT A out “input string” in SFT B A and B not equivalent out Algorithms use SMT for satisfiability checking of character formulas July 18, 2015 SMT'15, San Fransisco 40

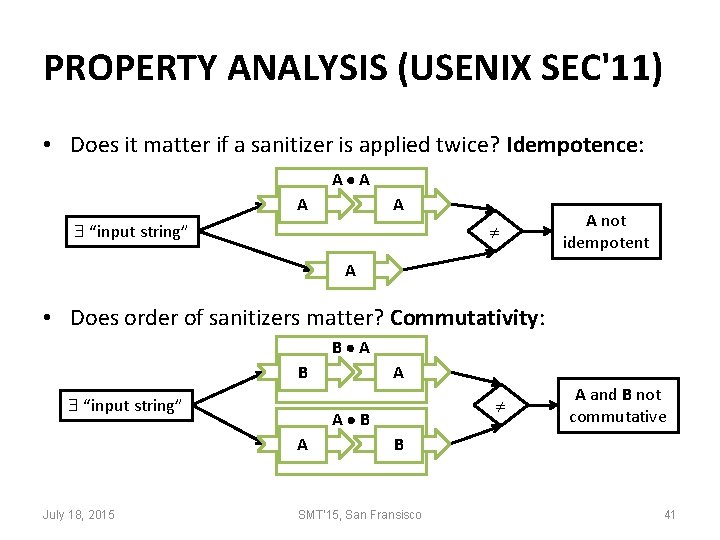
PROPERTY ANALYSIS (USENIX SEC'11) • Does it matter if a sanitizer is applied twice? Idempotence: A A “input string” A not idempotent A • Does order of sanitizers matter? Commutativity: B A B “input string” A B A July 18, 2015 A A and B not commutative B SMT'15, San Fransisco 41

APPLICATIONS July 18, 2015 SMT'15, San Fransisco 42

APPLICATIONS OF SFAS/SFTS • SFAs: – Regex support in parameterized unit testing – Fuzz testing of regexes – Password generation • SFTs: – Analysis of string encoders/decoders – Security analysis of sanitizers July 18, 2015 SMT'15, San Fransisco 43

APPLICATION 1 REGEXES IN PARAMETERIZED UNIT TESTING • Rex component in Pex • Generate values for s that reach the return branches – s is a string of Unicode characters (16 -bit bit-vectors) bool Is. Valid. Email(string s) { string r 1 = @"^[A-Za-z 0 -9]+@(([A-Za-z 0 -9-])+. )+([A-Za-z-])+$"; string r 2 = @"^d. *$"; if (System. Text. Regular. Expressions. Regex. Is. Match(s, r 1)) if (System. Text. Regular. Expressions. Regex. Is. Match(s, r 2)) return false; //branch 1 else Solve: s L(r 1) L(r 2) [eg. s = “ 3@a. b”] return true; //branch 2 else return false; //branch 3 Solve: s L(r 1)L(r 2) [eg. s = “a@b. c”] } Solve: s L(r 1) July 18, 2015 SMT'15, San Fransisco [eg. s = “a@. . c”] 44

APPLICATION 2 PASSWORD GENERATION Given constraints: • Length is k: "^[x 21 -x 7 E]{k}$" • Contains 2 capital letters: "[A-Z]. *[A-Z]" • Contains a digit: "d" • Contains a non-word character: "W" Generate random instances with uniform distribution that match all the above conditions. k=4 : http: //www. rise 4 fun. com/Rex/4 n. E http: //www. rise 4 fun. com/Bek/c 3 j July 18, 2015 SMT'15, San Fransisco 45

APPLICATION 3 SAFETY ANALYSIS Example: suppose good output = “No. Ears" No. Ears = [^u. DE 38 -u. DE 40]* bad output: With. Ears = Complement(No. Ears) x(smileycipher(x) With. Ears) ? {x | smileycipher(x) With. Ears} Does there exist an input x that causes “ears" in the output ? http: //www. rise 4 fun. com/Bek/5 s. HO July 18, 2015 SMT'15, San Fransisco 46

EXTENSIONS July 18, 2015 SMT'15, San Fransisco 47

EXTENSIONS OF SFAS AND SFTS • ESFT – SFA/SFTswith look-ahead [CAV'13] – BEX language • STT – Symbolic automata/transducer over trees – FAST language [PLDI’ 14] • k-SFT – SFT with lookback [POPL’ 15] July 18, 2015 SMT'15, San Fransisco 48

ESFAS AND ESFTS • Unlike in the classical case look-ahead breaks many properties – e. g. equivalence of ESFAs is undecidable x 1≤FF ∧ x 2≤FF ∧ x 3≤FF / [x 1>>2, ((x 1&3)<<4)|(x 2>>4), ((x 2&0 x. F)<<2)|(x 3>>6), x 3&0 x 3 F] q above ESFT, reads 3 and writes 4 symbols (base 64 encoder) M a n TWF u http: //www. rise 4 fun. com/Bex/tutorial/guide July 18, 2015 SMT'15, San Fransisco 49

FAST (TREE TRANSDUCERS) • Trees are common input/output data structures – XML query, type-checking, etc… – Natural Language translators (from parse tree to parse tree) – Compilers/optimizers (from parse tree to parse tree) Compilers – Tree manipulating programs: data structures algorithms, ontologies etc… – Augmented Reality – http: //www. rise 4 fun. com/Fast/tutorial/guide July 18, 2015 SMT'15, San Fransisco 50

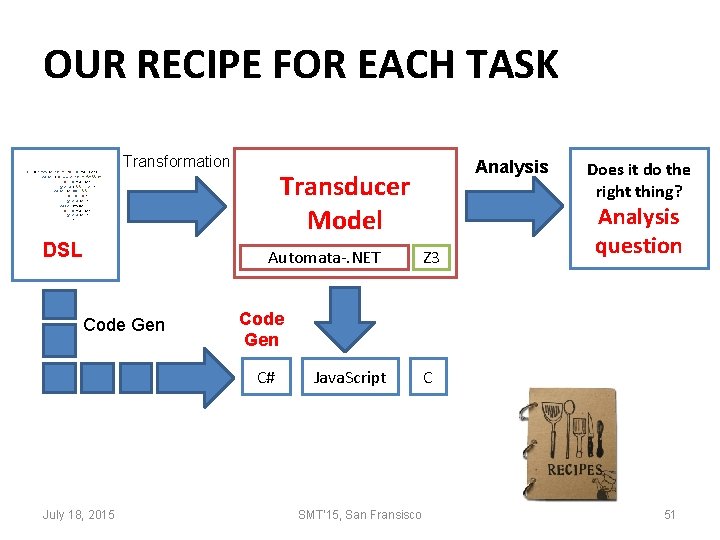
OUR RECIPE FOR EACH TASK s : = iter(c in t)[b : = false; ] { case (!b && c in "["\]"): b : = false; yield('\', c); case (c == '\'): b : = !b; yield(c); case (true): b : = false; yield(c); }; Transformation DSL Code Gen Transducer Model Automata-. NET Z 3 Does it do the right thing? Analysis question Code Gen C# July 18, 2015 Analysis Java. Script SMT'15, San Fransisco C 51

Automata-. NET will be open source on Git. Hub under MIT license Some references: BEK • Fast and precise sanitizer analysis with BEK Hooimeijer, Livshits, Molnar, Saxena, Veanes, USENIX 11 • Symbolic finite state transducers: algorithms and applications Veanes, Hooimeijer, Livshits, Molnar, Bjorner, POPL 12 BEX • Static analysis of string encoders and decoders D’Antoni, Veanes, VMCAI 13 • Equivalence of extended symbolic finite transducers D’Antoni, Veanes, CAV 13 • Data parallel string manipulating programs Veanes, Mytkowicz, Molnar, Livshits, POPL 15 July 18, 2015 SMT'15, San Fransisco 52

QUESTIONS? Links to related online tutorials: – Bek http: //rise 4 fun. com/Bek/tutorial – Bex http: //rise 4 fun. com/Bex/tutorial – Rex http: //rise 4 fun. com/rex/ – Fast http: //rise 4 fun. com/Fast/tutorial July 18, 2015 SMT'15, San Fransisco 53