String Metrics in Classification of Mobile Genetic Elements

String Metrics in Classification of Mobile Genetic Elements Discrete Mathematical Biology, Math 8803 Ryan Wagner Biology/Bioinformatics Ph. D student www. yale. edu/turner/projects/ecoli. htm www. geneticengineering. org/evolution http: //pdb. lbl. gov/microscopies

String Metrics in Classification of Mobile Genetic Elements 1. Mathematical relevance 2. Biological relevance 3. Test and review of four distance methods 4. What was “good, bad, and ugly”.

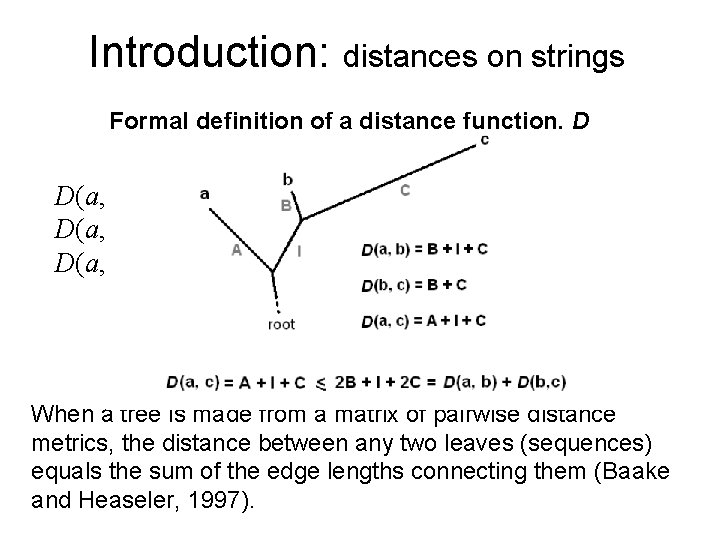
Introduction: distances on strings Formal definition of a distance function, D D(a, b) = 0 a = b, the identity axiom D(a, b) = D(b, a), the symmetry axiom D(a, b) + D(b, c) D(a, c), the triangle inequality Tree Additivity When a tree is made from a matrix of pairwise distance metrics, the distance between any two leaves (sequences) equals the sum of the edge lengths connecting them (Baake and Heaseler, 1997).

Introduction: mathematical distance vs. evolutionary distance • the three metric properties comprise the basis for characterization • when obtained by common statistical correction techniques, fails to satisfy the triangle inequality • may also be characterized by Turing Machine computability (Ahlbrandt et al. , 2004) • the tree additivity property may hold where the triangle inequality fails • amenable to both alignmentbased and alignment-free methods • not developed for alignment-free distances on DNA strings

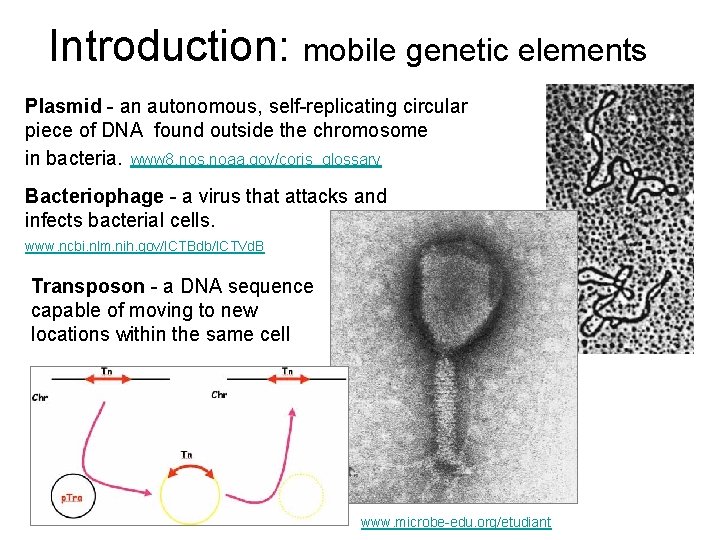
Introduction: mobile genetic elements Plasmid - an autonomous, self-replicating circular piece of DNA found outside the chromosome in bacteria. www 8. nos. noaa. gov/coris_glossary Bacteriophage - a virus that attacks and infects bacterial cells. www. ncbi. nlm. nih. gov/ICTBdb/ICTVd. B Transposon - a DNA sequence capable of moving to new locations within the same cell www. microbe-edu. org/etudiant

Methods: data collection and software • DNA sequences for replication initiation (Rep. A) and division partition (Par. A) in both plasmids and host chromosomes obtained from NCBI, www. ncbi. nlm. nih. gov/genomes/lproks. cgi • DNA sequences of selected plasmids from gram-negative bacteria also obtained from NCBI • Neighbor-joining trees constructed for each set of pairwise distances using PHYLIP, http: //evolution. genetics. washington. edu/phylip. html • Custom Perl script used to generate matrices of pairwise distances: 4 G_lovleyi Acidovoro Acid_JS 42 Xanth_axo 0. 000000 0. 864000 0. 887000 0. 844000 0. 864000 0. 000000 0. 664000 0. 724000 0. 887000 0. 664000 0. 000000 0. 836000 0. 844000 0. 724000 0. 836000 0. 000000

Methods: edit distance Data structure in custom script for test input: ATTGCGAGC and ATGCGACC A T T G C G A G C 0 1 2 3 4 5 6 7 8 9 A 1 0 1 2 3 4 5 6 7 8 T 2 1 0 1 2 3 4 5 6 7 G 3 2 1 2 3 4 5 6 C 4 3 2 1 2 3 4 5 G 5 4 3 2 1 2 3 4 A 6 5 4 3 2 1 2 3 C 7 6 5 4 3 2 Levenshtein distance = 3, from lower right corner, no traceback needed Here is where horizontal gene transfer begins to cause problems. C 8 7 6 5 4 3

Methods: the problem with edit distance Consider GTGACGTACTATTGC_ and GTGAGTACTATTGCC Consider GTGACGTACTATTGC_ and GTACTATTGCGTGAC 1 character delete/insert Edit distance = 2 5 character delete/insert Edit distance = 8 Allowing block deletions, block insertions, and block reversals confers better approximations to the recombinant nature of DNA evolution (Long-Hui, 2004). However, the least-constrained application of block edit distance has O(n 3) time complexity. Constrained block edit distance computation is NP-hard (Lopresti and Tomkins, 1997)

Methods: Euclidean distance over dinucleotide counts A new paradigm: complexity-based distance metrics which do not employ alignments nor dynamic programming a = GTGACGTACTATTGC b = GTACTATTGCGTGAC L 2 = (1/16)[∑ | a*ij b*ij |], where a*ij = freq(ij)/(freq(i) freq(j)) here L 2 = 0 Computation of counts vectors for a and b dinucleotide a b L 2 TCTC + GA 1 1 0 TGTG + CA 2 2 0 CTCT + AG 1 1 0 ACAC + GT 4 4 0 TTTT + AA 1 1 0 + GG CCCC + GG 0 0 0 CGCG 1 1 0 ATAT 1 1 0 GCGC 1 1 0 TATA 2 2 0

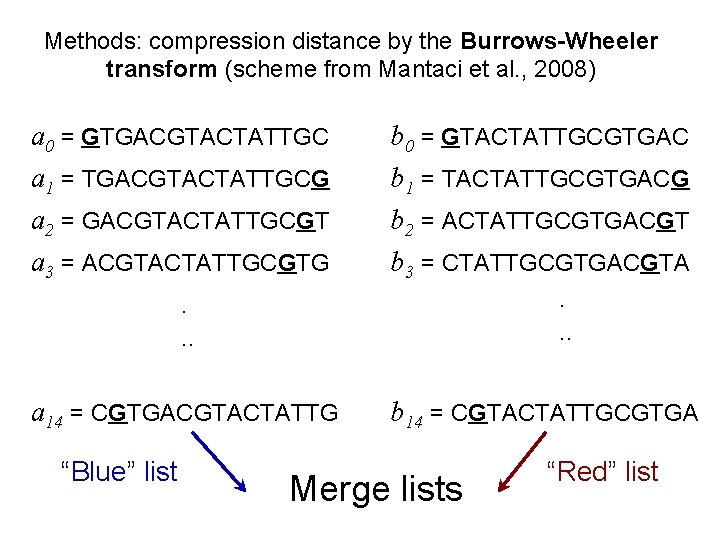
Methods: compression distance by the Burrows-Wheeler transform (scheme from Mantaci et al. , 2008) a 0 = GTGACGTACTATTGC b 0 = GTACTATTGCGTGAC a 1 = TGACGTACTATTGCG a 2 = GACGTACTATTGCGT a 3 = ACGTACTATTGCGTG. . . b 1 = TACTATTGCGTGACG b 2 = ACTATTGCGTGACGT b 3 = CTATTGCGTGACGTA. . . a 14 = CGTGACGTACTATTG b 14 = CGTACTATTGCGTGA “Blue” list Merge lists “Red” list

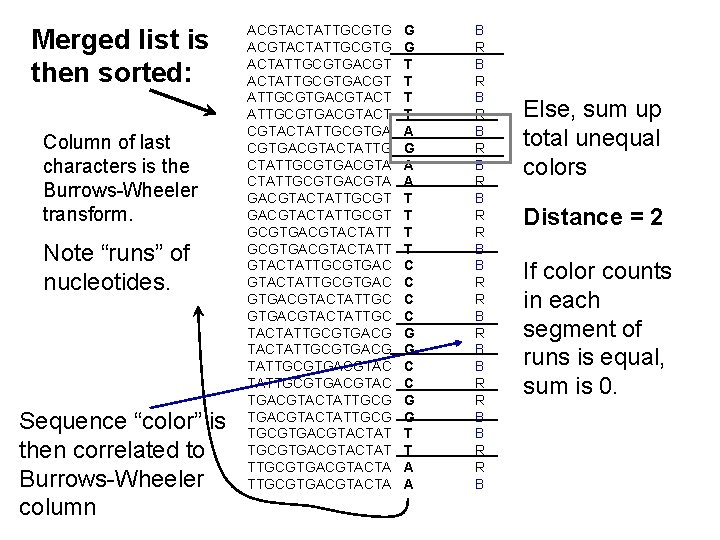
Merged list is then sorted: Column of last characters is the Burrows-Wheeler transform. Note “runs” of nucleotides. Sequence “color” is then correlated to Burrows-Wheeler column ACGTACTATTGCGTGACGT ATTGCGTGACGTACTATTGCGTGACGTACTATTGCGTGACGTACTATTGCGTGACGTACTATTGCGTGACGTACTATTGCGTGACG TATTGCGTGACGTACTATTGCGTGACGTACTAT TTGCGTGACGTACTA G G T T A G A A T T C C G G T T A A B R B R B R R B B R R B Else, sum up total unequal colors Distance = 2 If color counts in each segment of runs is equal, sum is 0.

Methods: “rank” distance Related to Hamming distance, but less sensitive to insertions/deletions (from Dinu and Sgarro, 2006) a = GTGACGTACTATTGC b = GTACTATTGCGTGAC Index each base and correlate it to its position in the sequence relative to the other sequence: • e. g. count the first occurrence of G in a and b, compute the difference in their positions, • count the second occurrence of G in a and b, compute the difference in their positions, …

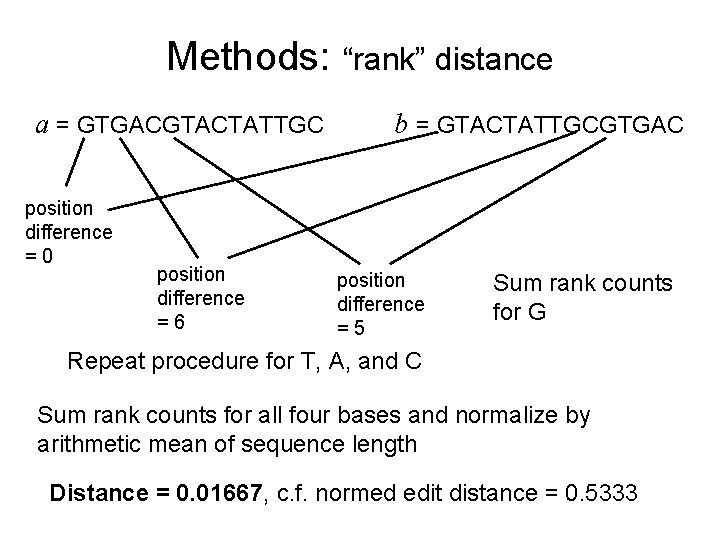
Methods: a = GTGACGTACTATTGC position difference =0 position difference =6 “rank” distance b = GTACTATTGCGTGAC position difference =5 Sum rank counts for G Repeat procedure for T, A, and C Sum rank counts for all four bases and normalize by arithmetic mean of sequence length Distance = 0. 01667, c. f. normed edit distance = 0. 5333

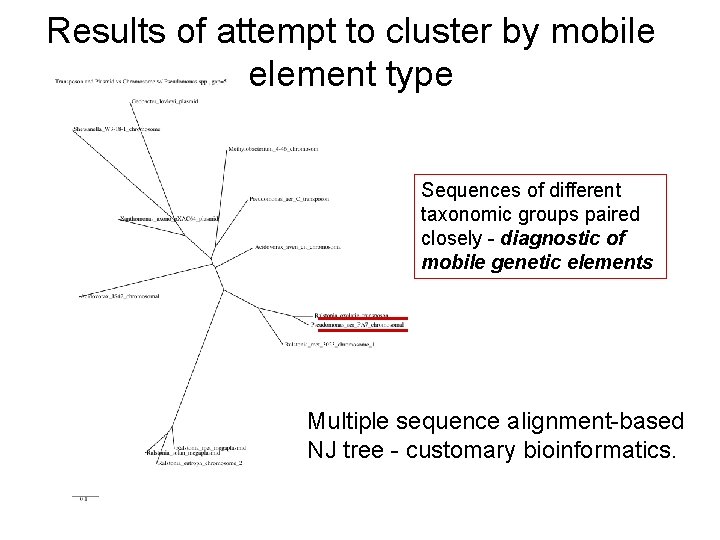
Results of attempt to cluster by mobile element type Sequences of different taxonomic groups paired closely - diagnostic of mobile genetic elements Multiple sequence alignment-based NJ tree - customary bioinformatics.

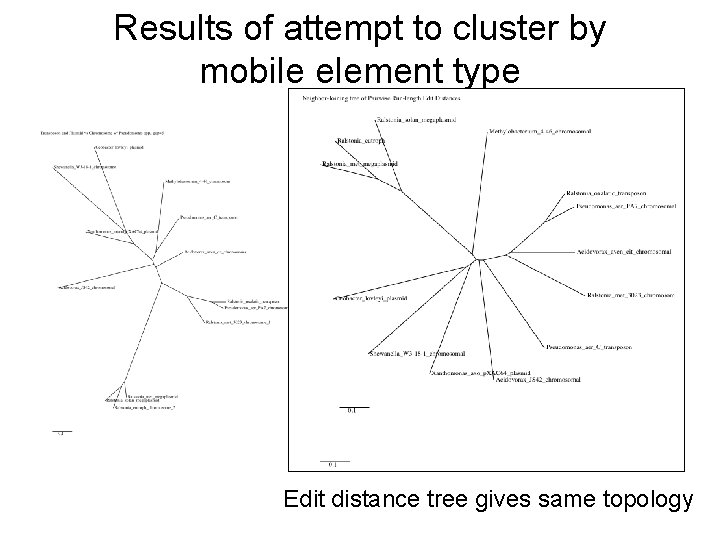
Results of attempt to cluster by mobile element type Edit distance tree gives same topology

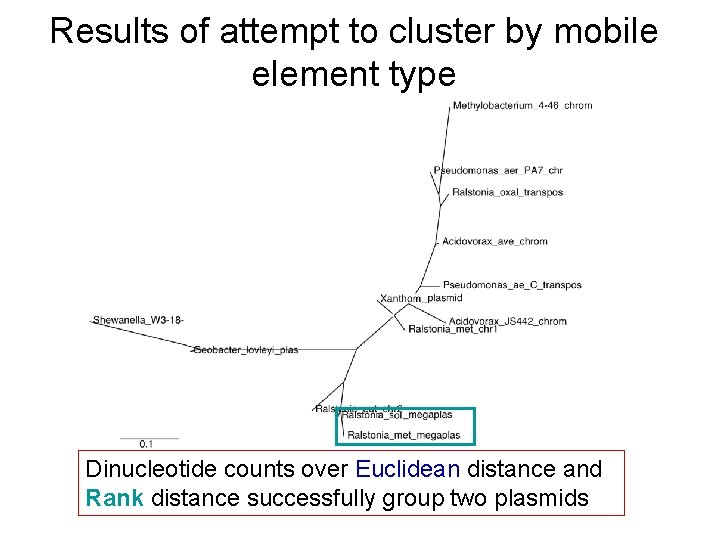
Results of attempt to cluster by mobile element type Dinucleotide counts over Euclidean distance and Rank distance successfully group two plasmids

Results of attempt to cluster by mobile element type Burrows-Wheeler compression pairwise distances do not give a clear clustering.

Why did the BWT distances not perform well? Rep. A-Par. A sequence data were too short for useful shared repeat regions to appear. Remedy: Run complete plasmid sequences through BWT distance script Insurmountable problem: the BWT distance script, as given, could not compute distances on whole plasmids. Diagnosis: time-complexity of BWT is O(n·log(n)), but space complexity is O(n 2) Mantaci et al. also found their BWT distance does not satisfy the triangle inequality (2008)

Can dinucleotide counts or rank distance be made to perform better in separating mobile elements? Li et al (2004) used trinucleotide counts combined with higher-order nucleotide word counts to accurately infer an evolutionary tree of mammalian mitochondrial DNA. Such simple methods cannot hope to approximate Kolomogorov complexity distance. Recall that Kolmogorov complexity is related to the length of the Turing Machine needed to transform sequence a into sequence b (Li et al. , 2004).

Open issues • So far, only dinucleotide counts have been developed for clustering of mobile elements (Blaisdell and Karlin, 1996) • BWT distance and Rank distance were developed to cluster mammalian mitochondrial DNA (Mantaci et al. , 2008; Dina and Sgarro, 2006). • Rank distance not shown to satisfy triangle inequality • Can it be proven whether or not a pairwise distance satisfying the triangle inequality yields an additive tree.

References Ahlbrandt, C. , Benson, G. , and Casey, W. (2004) “Minimal entropy probability between genome families. ” Journal of Mathematical Biology. 48: 563 -590. Baake, E. (1998) “What can and cannot be inferred from pairwise sequence comparisons? ” Mathematical Biosciences. 154: 1 -21 Blaisdell, B. E. , Campbell, A. M. , and Karlin, S. (1996) “Similarities and dissimilarities of phage genomes. ” Proc. Natl. Acad. Sci. 93: 5854 -5859. Dinu, L. P. and Sgarro, A. (2006) “A low-complexity distance for DNA strings. ” Fundamenta Informaticae. 76: 361 -372. Li. M, Chen, X. , Li, X. , Ma, B. , and Vianyi, P. (2004) “The similarity metric. ” IEEE Transactions on Information Theory XX(Y) Long-Hui, W. , Juan, L. , Zhou, H-B. , and Feng, Shi. (2004) "A new distances metric and its application in phylogenetic tree construction. " Proceedings of the 2004 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology. Lopresti, D. and Tomkins, A. (1997) "Block edit models for approximate string matching. " Theoretical Computer Science. 181: 159 -179 Mantaci, S. , Restivo, A. , and Sciortino. (2008) “Distance measure for biological sequences: Some recent approaches. ” International Journal of Approximate Reasoning. 47: 109 -124.