String Data Structures and Algorithms Suffix Trees and

String Data Structures and Algorithms: Suffix Trees and Suffix Arrays David Fernández-Baca UNAM (Mexico) (based on notes by Srinivas Aluru) Summer School - Iowa State slightly BBSI modified by Benny Chor University

Why Strings? • Biological sequences can be viewed as strings, or finite series of characters, over an alphabet Σ. • There is a wealth of algorithmic theory developed for general strings that we can apply to specific biological problems. 6/4/2021 BBSI Summer School - Iowa State University 2

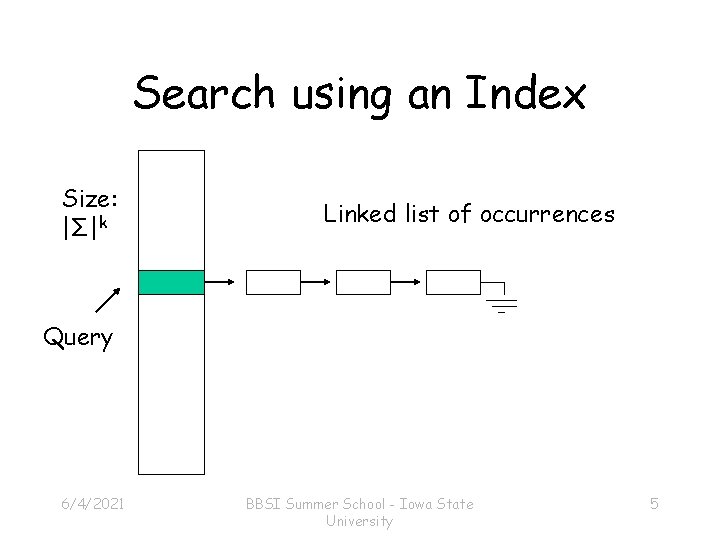
Look-up Tables • Strings of length k over Σ can be represented by an integer index i, 0 ≤ i ≤ Σk – 1. • DNA is composed of four characters. – Σ = {A, G, C, T} |Σ| = 4 • We can preprocess a database into a lookup table to locate all occurrences of a query index. 6/4/2021 BBSI Summer School - Iowa State University 3

Example Let: A = 0 (00) C = 1 (01) G = 2 (10) T = 3 (11) Strings are converted based on the binary string they represent String AAA ATA AAC 6/4/2021 Binary = = = 000000 001100 000001 Integer = 0 = 12 = 1 BBSI Summer School - Iowa State University 4

Search using an Index Size: |Σ|k Linked list of occurrences Query 6/4/2021 BBSI Summer School - Iowa State University 5

Applications of Indexing • Seeds for searching sequence databases – BLAST • Pair generation for fragment assembly in sequencing projects – CAP 3 sequence assembly program 6/4/2021 BBSI Summer School - Iowa State University 6

Indexing • Using a sparse representation, a database can be preprocessed in linear time to allow locating all instances of a short string. • Major limitation: search is restricted to fixed length strings. 6/4/2021 BBSI Summer School - Iowa State University 7

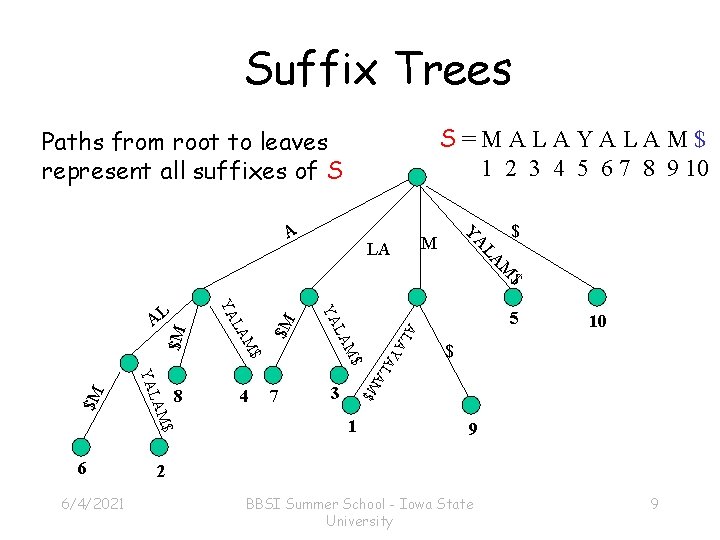
Suffix Trees S=MALAYALAM$ 1 2 3 4 5 6 7 8 9 10 Paths from root to leaves represent all suffixes of S M $M $M A L AY A 6/4/2021 7 5 10 $ L A M$ M$ $ LAM YA 6 LA 4 $ M LA 8 YA YA AL $M $ M LA LA $ YA A 3 1 9 2 BBSI Summer School - Iowa State University 9

Suffix tree properties • For a string S of length n, there are n+1 leaves and at most n internal nodes. – therefore requires only linear space, provided edge labels are O(1) space • Each leaf represents a unique suffix. • Concatenation of edge labels from root to a leaf spells out the suffix. • Each internal node represents a distinct common prefix to at least two suffixes. 6/4/2021 BBSI Summer School - Iowa State University 10

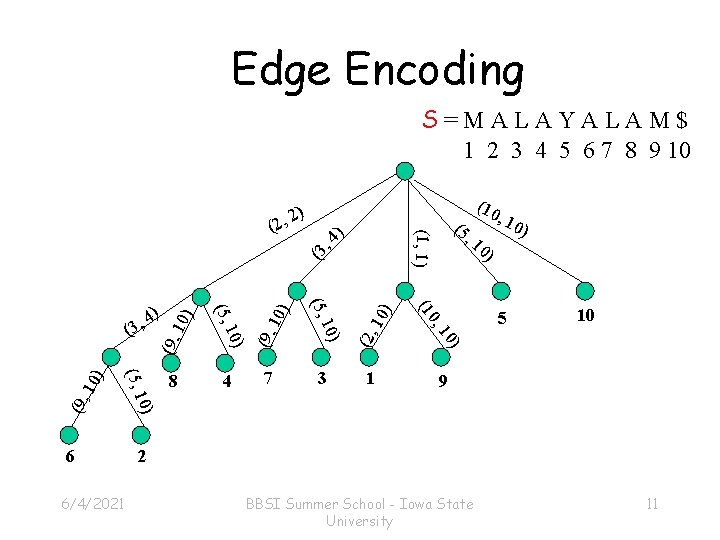
Edge Encoding S=MALAYALAM$ 1 2 3 4 5 6 7 8 9 10 (2, 10 ) , 4 ) (3 10) (9, 10 ) 1 9 0) 5 10 0) 3 , 1 (9, 0 (1 7 10) 6/4/2021 4 , 10 ) 0) (5, 1 6 8 (5, ) 4 , 3 ( (10 (5 (1, 1) ( (5, ) 2, 2 2 BBSI Summer School - Iowa State University 11

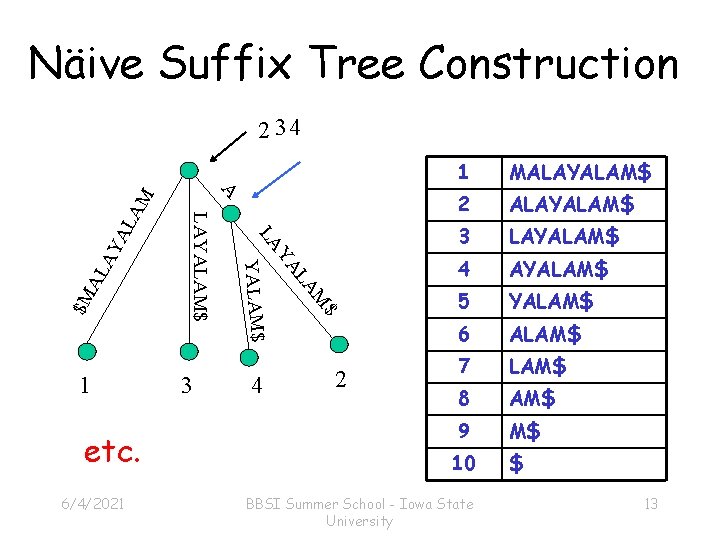
Näive Suffix Tree Construction Before starting: Why exactly do we need this $, which is not part of the alphabet? 1 MALAYALAM$ 2 ALAYALAM$ 3 LAYALAM$ 4 AYALAM$ 5 YALAM$ 6 ALAM$ 7 LAM$ 8 AM$ 9 M$ 10 6/4/2021 BBSI Summer School - Iowa State University $ 12

Näive Suffix Tree Construction 2 34 AL $M $ M 4 LA YA YALAM$ 6/4/2021 3 LA AY AL A M A etc. LAYALAM$ 1 2 1 MALAYALAM$ 2 ALAYALAM$ 3 LAYALAM$ 4 AYALAM$ 5 YALAM$ 6 ALAM$ 7 LAM$ 8 AM$ 9 M$ 10 BBSI Summer School - Iowa State University $ 13

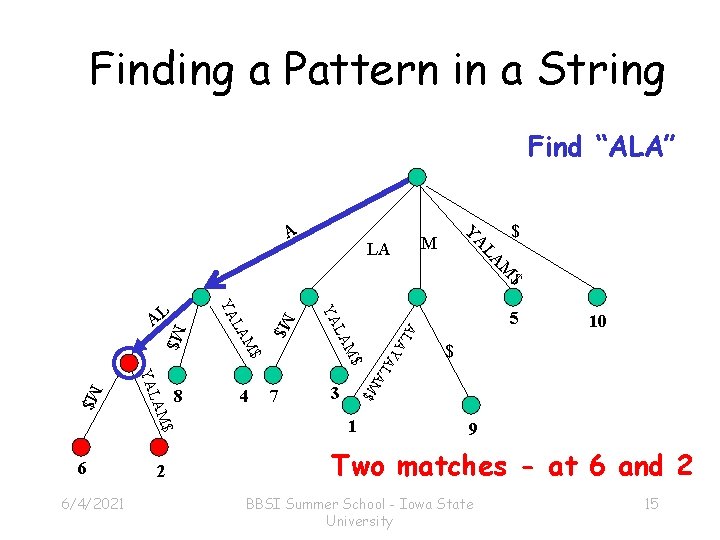
Application: Finding a short Pattern in a long String 1. Build a suffix tree of the string. 2. Starting from the root, traverse a path matching characters of the pattern. 3. If stuck, pattern not present in string. Otherwise, each leaf below gives a position of the pattern in the string. 6/4/2021 BBSI Summer School - Iowa State University 14

Finding a Pattern in a String Find “ALA” M $ M LA LA $ YA A A L AY A 7 5 10 $ L A M$ M$ 6/4/2021 2 LA $ LAM YA M$ 6 YA 4 $ M LA 8 M$ YA M$ AL 3 1 9 Two matches - at 6 and 2 BBSI Summer School - Iowa State University 15

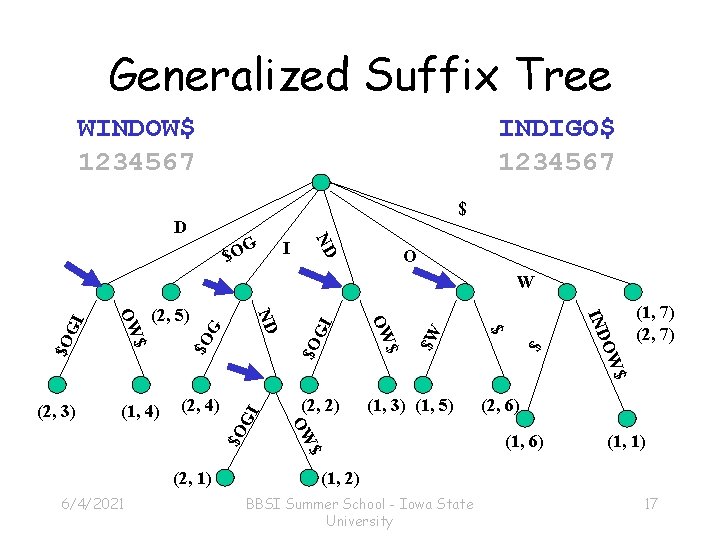
Finding Common Sub. Strings • Construct a generalized suffix tree for two strings (each suffix of each string is represented). • Label each leaf with the suffix number and string label. • Each internal node with a leaf from both strings in its subtree gives a common substring. 6/4/2021 BBSI Summer School - Iowa State University 16

Generalized Suffix Tree WINDOW$ 1234567 D INDIGO$ 1234567 $ I ND G $O O $O GI 6/4/2021 $ $W GI $O $O G $O $ OW (2, 1) $ OW (1, 3) (1, 5) IND (2, 2) $ (2, 4) $ (1, 4) OW (2, 5) ND (2, 3) $ OW GI W (1, 7) (2, 6) (1, 1) (1, 2) BBSI Summer School - Iowa State University 17

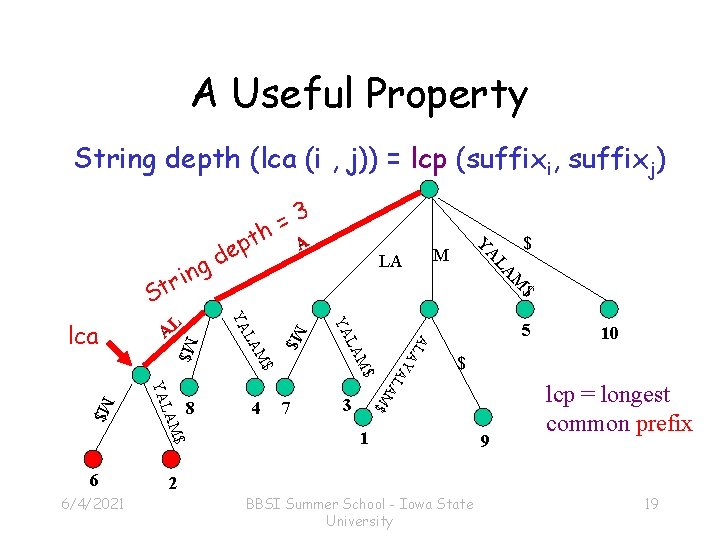
Lowest Common Ancestors • The lowest common ancestor (lca) of two nodes x and y in a rooted tree is the deepest node (farthest away from root) that is an ancestor of both x and y • Concatenation of edge labels from root to the lca of two leaves spells out the longest common prefix (lcp) of two strings • lca(x, y) an be found in constant time after linear preprocessing [Bender 00] 6/4/2021 BBSI Summer School - Iowa State University 18

A Useful Property String depth (lca (i , j)) = lcp (suffixi, suffixj) $ A L AY A 7 5 3 10 $ L A M$ M$ 6/4/2021 LA $ LAM YA M$ 6 YA 4 $ M LA 8 M$ YA M$ lca AL LA M $ r t S A M LA ing pt e d YA 3 = h 1 9 lcp = longest common prefix 2 BBSI Summer School - Iowa State University 19

Longest Common Extension GRAINY$ RAI 1234567 RAILWAY$ 12345678 lce(1, 1) = 0 lce(2, 1) = 3 We’ll soon find lce’s useful in reconstructing phylogenetic trees based on whole genome/proteome sequences 6/4/2021 BBSI Summer School - Iowa State University 20

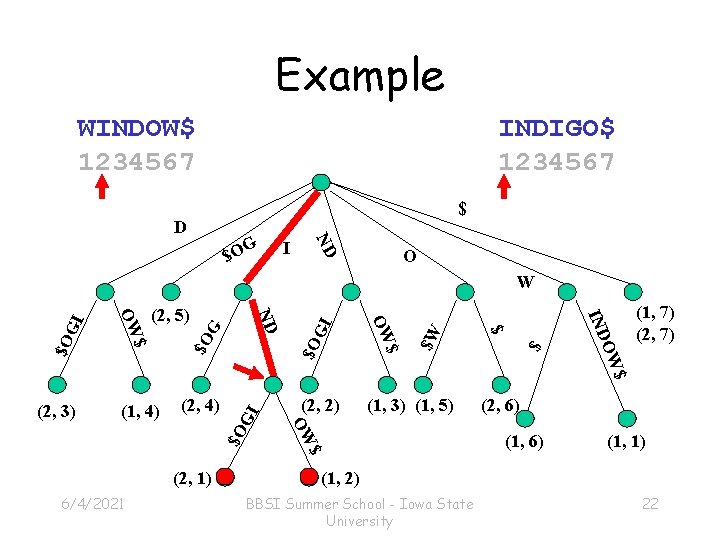
lce’s and lca’s To compute lce’s for two strings S 1 and S 2 1. 2. 3. 4. Build generalized suffix tree, T, of S 1 and S 2 Compute string depth for each node in T Preprocess T for lca queries lce(i, j) = string depth of lca of suffix i of. S 1 and suffix j of. S 2 6/4/2021 BBSI Summer School - Iowa State University 21

Example WINDOW$ 1234567 D INDIGO$ 1234567 $ I ND G $O O $O GI 6/4/2021 $ $W GI $O $O G $O $ OW (2, 1) $ OW (1, 3) (1, 5) IND (2, 2) $ (2, 4) $ (1, 4) OW (2, 5) ND (2, 3) $ OW GI W (1, 7) (2, 6) (1, 1) (1, 2) BBSI Summer School - Iowa State University 22

lce’s, revisited Given two strings S 1 and S 2 , we are now interested in finding, for each i, the index j such that lce (i, j) is maximal. 1. What is the meaning of this task? 2. How do we accomplish it efficiently? 3. Notice that computing the values lce (i, j) for all j is very inefficient! 6/4/2021 BBSI Summer School - Iowa State University 23

Palindromes • A palindrome is a string that reads the same in both directions – E. g. , CATGTAC – red rum, sir, is murder • Palindrome problem: Find all maximal palindromes in a string S 6/4/2021 BBSI Summer School - Iowa State University 24

Finding Palindromes in S 1. 2. 3. 4. Construct the reverse S’ of S Build generalized suffix tree of S and S’ Preprocess T for lce queries Now what? Left as homework Requirement: Linear time (const. per query) S q+1 6/4/2021 BBSI Summer School - Iowa State University 25

Palindromes in DNA sequences • We sometimes need to deal with Crick-Watson complemented palindromes A T C G • E. g. , ATCATGAT is a complemented palindrome • All complemented palindromes in S can be found using a GST of S and the complement of S’ 6/4/2021 BBSI Summer School - Iowa State University 26

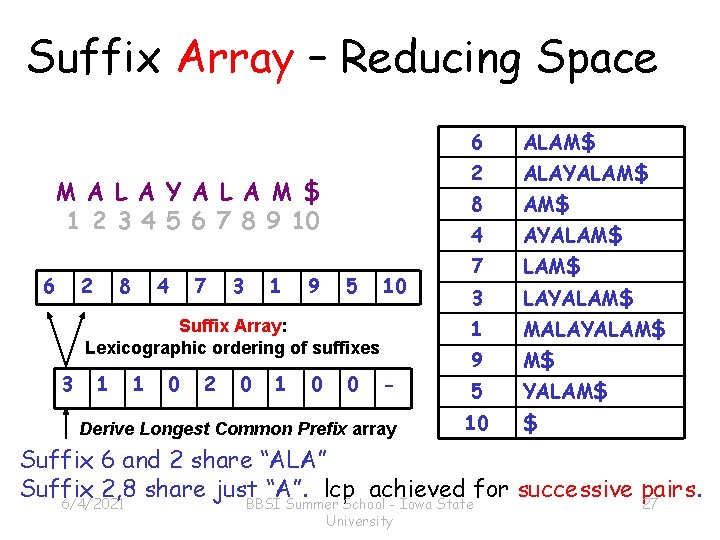
Suffix Array – Reducing Space M A L A Y A L A M $ 1 2 3 4 5 6 7 8 9 10 6 2 8 4 7 3 1 9 5 10 Suffix Array: Lexicographic ordering of suffixes 3 1 1 0 2 0 1 0 0 - Derive Longest Common Prefix array 6 ALAM$ 2 ALAYALAM$ 8 AM$ 4 AYALAM$ 7 LAM$ 3 LAYALAM$ 1 MALAYALAM$ 9 M$ 5 YALAM$ 10 $ Suffix 6 and 2 share “ALA” Suffix 2, 8 share just “A”. lcp achieved for successive pairs. 6/4/2021 BBSI Summer School - Iowa State University 27

Pattern Search in Suffix Array • All suffixes that share a common prefix appear in consecutive positions in the array. • Pattern P can be located in the string using a binary search on the suffix array. Naïve Run-time = O(|P| log n). Improved to O(|P| + log n) [Manber&Myers 93], and to O(|P|) [Abouelhoda et al. 02]. 6/4/2021 BBSI Summer School - Iowa State University 28

Example Text M A L A Y A L A M $ Position 1 2 3 4 5 6 7 8 9 10 Suffix Array 6 2 8 4 7 3 1 9 5 10 3 1 1 0 2 0 1 0 0 lcp Array 6/4/2021 BBSI Summer School - Iowa State University 6 ALAM$ 2 ALAYALAM$ 8 AM$ 4 AYALAM$ 7 LAM$ 3 LAYALAM$ 1 MALAYALAM$ 9 M$ 5 YALAM$ 10 $ 30

Suffix Trees vs. Suffix Arrays Suffix Array = Lexicographic order of the leaves of the Suffix Tree Suffix Array + lcp Array (why? Wait for next slide) 6/4/2021 BBSI Summer School - Iowa State University 31

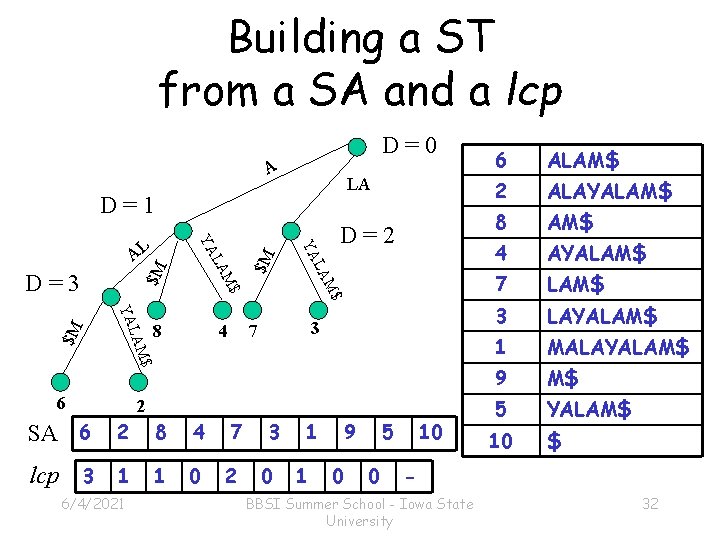
Building a ST from a SA and a lcp 6 ALAM$ 2 ALAYALAM$ 8 AM$ 4 AYALAM$ 7 LAM$ 3 LAYALAM$ 1 MALAYALAM$ $ D=0 9 M$ 2 5 YALAM$ A LA D=1 $M $M $M 8 4 4 M$ 8 3 7 7 LA 2 M$ LAM YA 6 SA 6 LA D=3 YA YA AL D=2 3 1 9 5 10 10 $ lcp 3 1 1 0 2 0 1 0 0 6/4/2021 BBSI Summer School - Iowa State University 32

Known (amazing) Results 1. Suffix tree can be constructed in O(n) time and O(n |∑|) space [Weiner 73, Mc. Creight 76, Ukkonen 92]. 2. Suffix arrays can be constructed without using suffix trees in O(n) time [Pang&Aluru 03]. 6/4/2021 BBSI Summer School - Iowa State University 33

More Applications • Suffix-prefix overlaps in fragment assembly • Maximal and tandem repeats • Shortest unique substrings • Maximal unique matches [MUMmer] • Approximate matching • Phylogenies based on complete genomes 6/4/2021 BBSI Summer School - Iowa State University 34

Dealing with errors • The basic string data structures can only extract information in the absence of errors. • To deal with errors, decompose into parts that do not involve errors. 6/4/2021 BBSI Summer School - Iowa State University 35

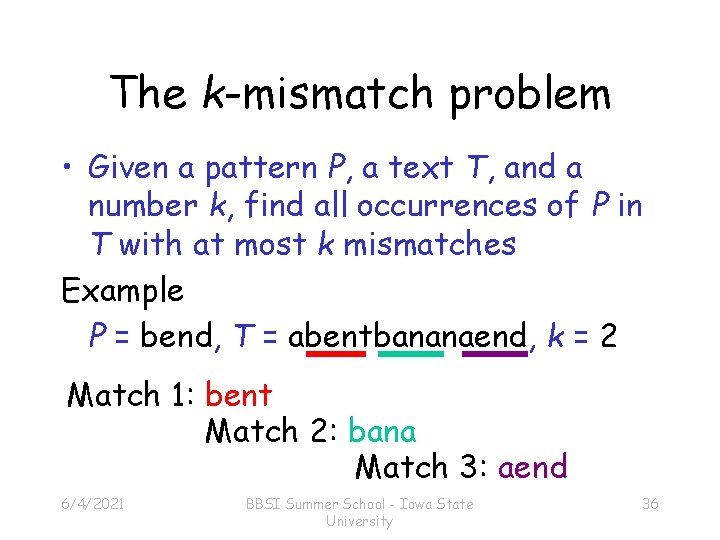
The k-mismatch problem • Given a pattern P, a text T, and a number k, find all occurrences of P in T with at most k mismatches Example P = bend, T = abentbananaend, k = 2 Match 1: bent Match 2: bana Match 3: aend 6/4/2021 BBSI Summer School - Iowa State University 36

Solution 1. Build GST of P and T and preprocess it for lce queries 2. For each starting index i in T, do at most k lce queries to determine if there is a k-mismatch beginning at i T P 6/4/2021 Time = O(k |T |) BBSI Summer School - Iowa State University 37

References • • M. I. Abouelhoda, S. Kurtz and E. Ohlebusch, The enhanced suffix array and its applications to genome analysis, 2 nd Workshop on Algorithms in Bioinformatics, pp. 449 -463, 2002. M. A. Bender and M. Farach-Colton, The LCA Problem Revisited, LATIN, pages 88 -94, 2000. P. Ko and S. Aluru, Linear time suffix sorting, CPM, pages 200 -210, 2003. U. Manber and G. Myers. Suffix arrays: a new method for on-line search, SIAM J. Comput. , 22: 935 -948, 1993. E. M. Mc. Creight, A space-economical suffix tree construction algorithm, J. ACM, 23(2): 262 --272, 1976. E. Ukkonen, Constructing suffix trees on-line in linear time. Intern. Federation of Information Processing, pp. 484 -492, 1992. Also in Algorithmica, 14(3): 249 --260, 1995. P. Weiner, Linear pattern matching algorithms, Proc. of the 14 th IEEE Annual Symp. on Switching and Automata Theory, pp. 1 -11, 1973. 6/4/2021 BBSI Summer School - Iowa State University 38