Stress Strain Elasticity Items to be covered Direct

Stress, Strain & Elasticity Items to be covered: • Direct Tensile Stress • Direct Compressive stress • Relationship in terms of Modulus of elasticity • Ultimate & Yield Stress • Reduced working or Permissible stress • Factor of Safety

A word on Units used • Stress = Force per unit area, • Units are k. N/m 2 or N/mm 2 • Mass units are in Kilograms but in Structural Analysis we use Weight units which is Force exerted on a body by the gravitational pull of the earth. (called Newtons) • Mass to Force (acceleration due to Gravity is 9. 81 m/s 2): 100 Kg x 9. 81 m/s 2 = 981 N (nearly 1000 N = 1 k. N)

Add meaning to the forces units: • Average mass of a small apple is 100 g (or 0. 1 kg) • • • Weight (In Newtons ) = 0. 1 kg x 9. 81 m/s 2 = 0. 981 N (approx 1 N) So 1000 apples = 1000 N = 1 k. N Large man weighs 100 Kg, which translates to: 100 kg x 9. 81 m/s 2 = 981 N or approx 1 k. N

1 N 1 k. N

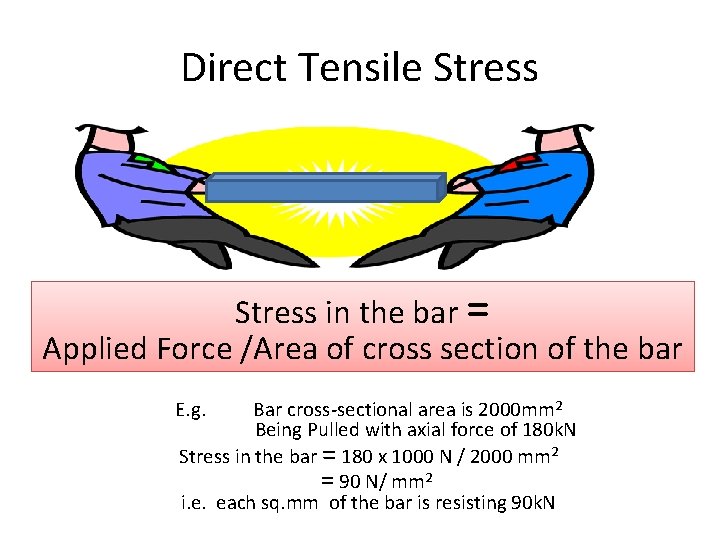
Direct Tensile Stress in the bar = Applied Force /Area of cross section of the bar E. g. Bar cross-sectional area is 2000 mm 2 Being Pulled with axial force of 180 k. N Stress in the bar = 180 x 1000 N / 2000 mm 2 = 90 N/ mm 2 i. e. each sq. mm of the bar is resisting 90 k. N

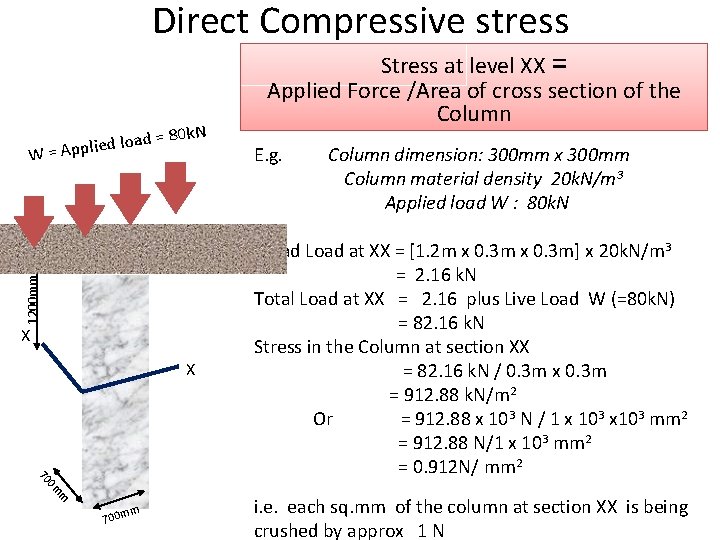
Direct Compressive stress 80 k. N 1200 mm W ad = o l d e i l p p =A X X m 0 m 70 700 m m Stress at level XX = Applied Force /Area of cross section of the Column E. g. Column dimension: 300 mm x 300 mm Column material density 20 k. N/m 3 Applied load W : 80 k. N Dead Load at XX = [1. 2 m x 0. 3 m] x 20 k. N/m 3 = 2. 16 k. N Total Load at XX = 2. 16 plus Live Load W (=80 k. N) = 82. 16 k. N Stress in the Column at section XX = 82. 16 k. N / 0. 3 m x 0. 3 m = 912. 88 k. N/m 2 Or = 912. 88 x 103 N / 1 x 103 mm 2 = 912. 88 N/1 x 103 mm 2 = 0. 912 N/ mm 2 i. e. each sq. mm of the column at section XX is being crushed by approx 1 N

Strain = Change in length / Original length = δl / l • Strain = Ratio of change of length of dimension to original length for a material under stress • A bar subject to a tensile force will slightly extend. • A column under pressure will slightly compress. (i. e. get shorter) • For elastic materials this change in dimension is proportional to the applied loads (Hooks Law)

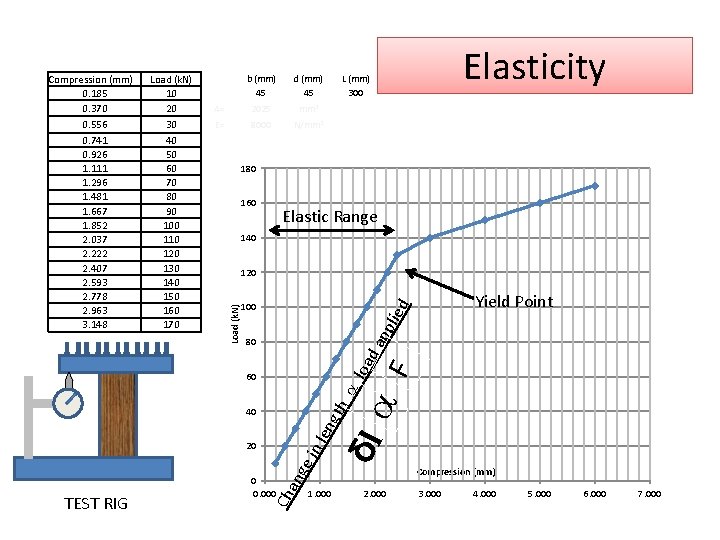
b (mm) 45 d (mm) 45 A= 2025 mm 2 E= 8000 N/mm 2 Elasticity L (mm) 300 180 160 Elastic Range 140 120 Yield Point da pp lied 100 80 F loa Load (k. N) 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 Load (k. N) Compression (mm) 0. 185 0. 370 0. 556 0. 741 0. 926 1. 111 1. 296 1. 481 1. 667 1. 852 2. 037 2. 222 2. 407 2. 593 2. 778 2. 963 3. 148 gth a a 60 ge an 0 0. 000 Ch TEST RIG in 20 1. 000 δl len 40 2. 000 Compression (mm) 3. 000 4. 000 5. 000 6. 000 7. 000

Modulus of Elasticity Or “Young’s Modulus” after Thomas Young • E = Stress / Strain ------ N/mm 2 or k. N/m 2 • Same units as stress, as strain is just a ratio of change in length to original length E = F A / E = F A x δl l l δl E E= F = δl Gradient of Graph x x l A

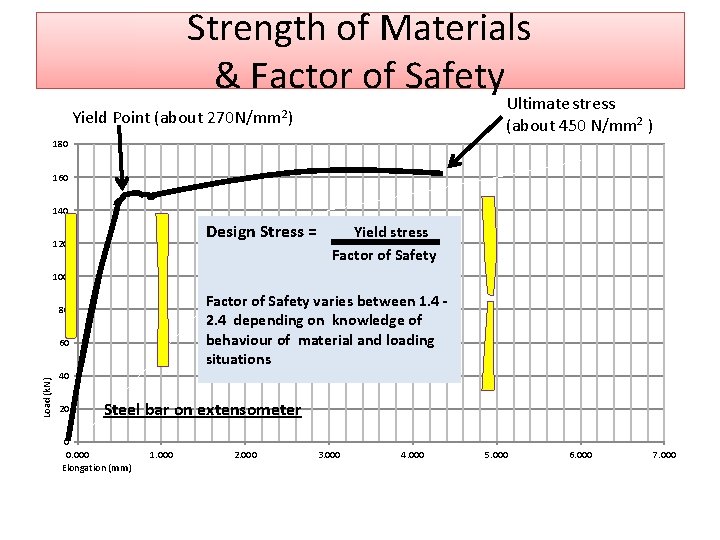
Strength of Materials & Factor of Safety Ultimate stress (about 450 N/mm 2 ) Yield Point (about 270 N/mm 2) 180 160 140 Design Stress = 120 Yield stress Factor of Safety 100 Factor of Safety varies between 1. 4 2. 4 depending on knowledge of behaviour of material and loading situations 80 Load (k. N) 60 40 20 Steel bar on extensometer 0 0. 000 Elongation (mm) 1. 000 2. 000 3. 000 4. 000 5. 000 6. 000 7. 000

1. 2. 3. Class Exercises A steel tie bar 100 mm x 10 mm in cross-section is transmitting a pull of 135 k. N. Calculate the stress in the bar. Calculate the safe tension load for a steel bar 75 mm x 6 mm in cross-section, the working stress being 155 N/mm 2 A tie bar is 75 mm wide and it has to sustain a pull of 100 k. N. Calculate the required thickness of the bar if the permissible stress is 150 N/mm 2 4. A bar of steel circular in cross-section is 25 mm in diameter. It sustains a pull of 60 k. N. Calculate the stress in the bar. 5. Calculate the safe load for a bar of steel 36 mm in diameter if the working stress is 155 N/mm 2 6. A bar of steel, circular in cross-section, is required to transmit a pull of 40 k. N. If the permissible stress is 150 N/mm 2 calculate the required diameter of the bar. 7. A timber tension member is 100 mm square in cross-section. Calculate the safe load for the timber if the permissible stress is 8 N/mm 2. Calculate the diameter of a steel bar which would be of equal strength to the timber member. Permissible stress for the steel is 150 N/mm 2 8. Calculate the cross-sectional dimensions of a square brick pier to support an axial load of 360 k. N, if the permissible stress for the brickwork is 1. 7 N/mm 2 9. A short specimen of deal timber 50 mm square in cross-section failed in a compression machine at a load of 70 k. N. The permissible stress for such timber is 5. 6 N/mm 2 Calculate the factor of safety. 10. A steel stanchion carrying a load of 877. 5 k. N is to be provided with a square steel base plate to spread the load on to a concrete foundation block. Calculate the minimum length of side (in mm) of the base plate if the stress on the concrete must not exceed 4. 5 N/mm 2 11. A steel column circular in cross-section is 150 mm in diameter and carries a load of 1. 2 MN. Calculate a) the compressive stress in the column; b) the length of side of a square steel base plate to transmit the column load to a concrete foundation block; the permissible stress on the concrete is 4. 5 N/mm 2; c) assuming the concrete base to weigh 150 k. N, calculate the plan dimensions of the concrete foundation so that the stress on the soil does not exceed 200 k. N/m 2