Stress Propagation in a Granular Column In Gravity

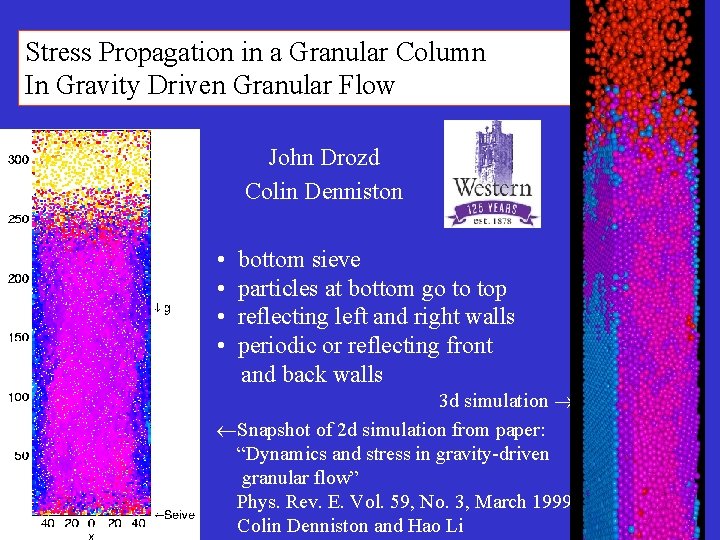
Stress Propagation in a Granular Column In Gravity Driven Granular Flow John Drozd Colin Denniston • • bottom sieve particles at bottom go to top reflecting left and right walls periodic or reflecting front and back walls 3 d simulation Snapshot of 2 d simulation from paper: “Dynamics and stress in gravity-driven granular flow” Phys. Rev. E. Vol. 59, No. 3, March 1999 Colin Denniston and Hao Li

Outline • • • Granular Matter Definition Why Study Granular Matter? Granular Column and Dynamics Profiles and Stresses From Simulation Continuum Mechanics Nonlinear Density Biharmonic PDE Model Perturbation Analysis Numerical Approach

Granular Matter • Granular matter definition – Small discrete particles vs. continuum. • Granular motion – Energy input and dissipation. • Granular matter interest – Biology, engineering, geology, material science, physics.

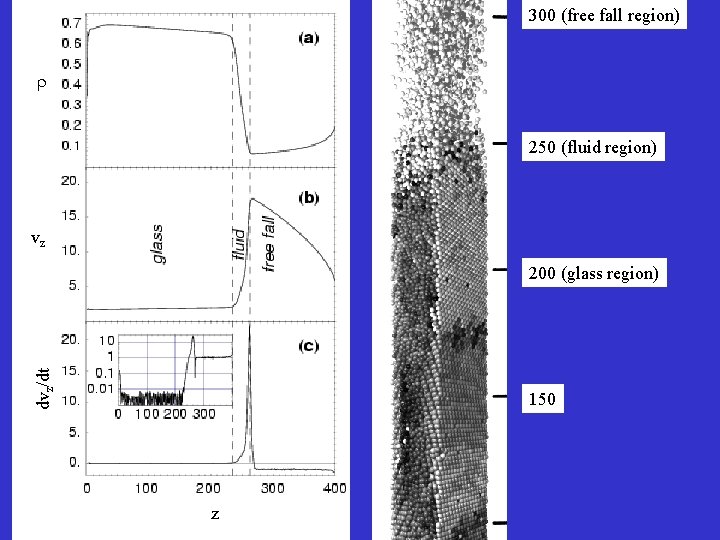
300 (free fall region) 250 (fluid region) vz dvz/dt 200 (glass region) 150 z

Hard Sphere Collision Velocity Adjustment q

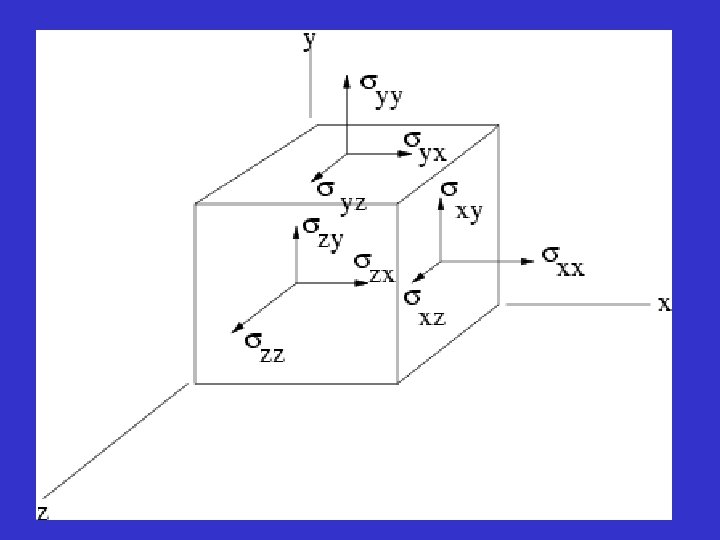
Stress Tensor Calculation

z h h' 0 X' w x Experimental data from the book: “Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials” By Jacques Duran.

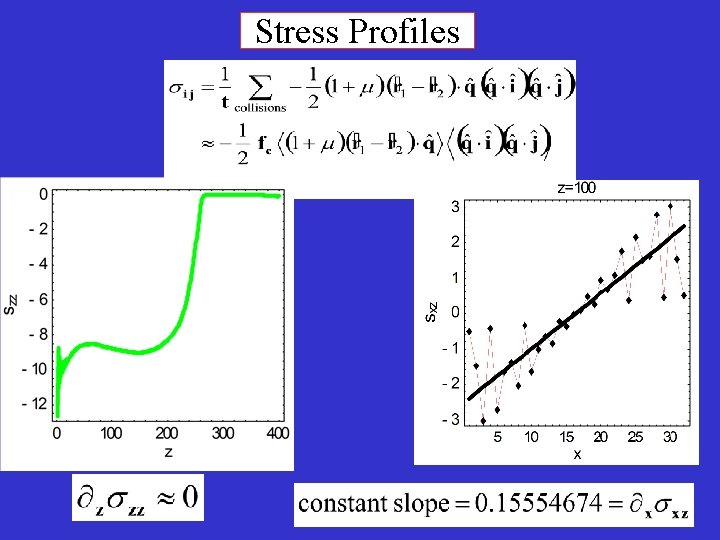
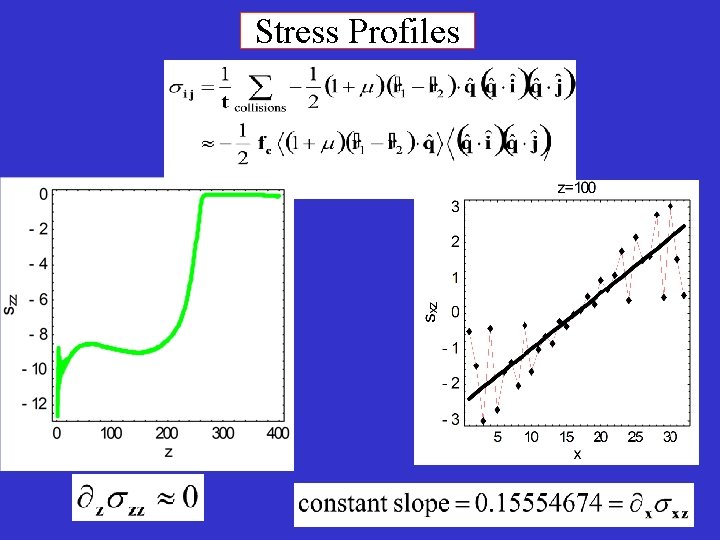
Stress Profiles

Continuum Mechanics (Two dimensional x-z model)

Continuum Mechanics

Continuum Mechanics

Continuum Mechanics Choose x and z along principal axes:

Continuum Mechanics

PDE

Nonlinear Density and Biharmonic PDE For isotropic hard spheres t = r = s = 1:

Boundary Conditions z h h' 0 X' w x

Stress Profiles

0 using Solving terms of order separation of variables

Solving terms of order 1 using Fourier transforms

Solving terms of order 1 using Fourier transforms

Solving terms of order 1 using Fourier transforms

Solving terms of order 1 using Fourier transforms

Experimental data from the book: “Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials” By Jacques Duran.

Hypergeometric function

Solving terms of order 1 using Fourier transforms

Solving terms 2 and higher

Solution

Numerical Approach

Conclusions • Provided a perturbative analytical treatment for studying nonlinear stress propagation • Presented a finite difference numerical scheme to compare with the analytical solution. • Future work: To test this pde model by implementing these methods to get numerical values of stresses and compare with those from simulation, and extend the model for the anisotropic case.

random packing at early stage = 2. 75 Is there any difference between this glass and a solid? Answer: Look at Monodisperse grains crystallization at later stage = 4. 3 Disorder has a universal effect on Stresses and Collision Times.

THE END