STRENGTH OF MATERIALS UNIT II Beams Loads and

STRENGTH OF MATERIALS UNIT – II Beams – Loads and Stresses 1

INTRODUCTION • Structural Members are usually classified according to the types of loads that they support (axially loaded bar, etc. ) • Now we will begin to look at beams, which are structural members subjected to lateral loads. • The first beams we will investigate are called planar structures, because they lie in a single plane. • If all loads act in that same plane, and if all deflections act in that plane, then the plane is called the Plane of Bending. • First we will look at shear forces and bending moments in beams. • Once we know these, we can find the stresses, strains and deflections of a beam 2

TYPES OF BEAMS • Beams are usually described by the way they are supported. • Simply supported beam – pin support at one end a roller support at the other • Cantilever beam – fixed at one end and free at the other. • Beam with an Overhang – simply supported beam that projects beyond the support (similar to a cantilever).

TYPES OF LOADS • Concentrated Loads • Couple • Distributed Loads – Uniformly distributed – Linearly varying

Shear Force and Bending Moment ü Shear Force: The algebraic sum of the vertical forces acting to the left or right of a cut section along the span of the beam ü Bending Moment: The algebraic sum of the moment of the forces to the left or to the right of the section taken about the section

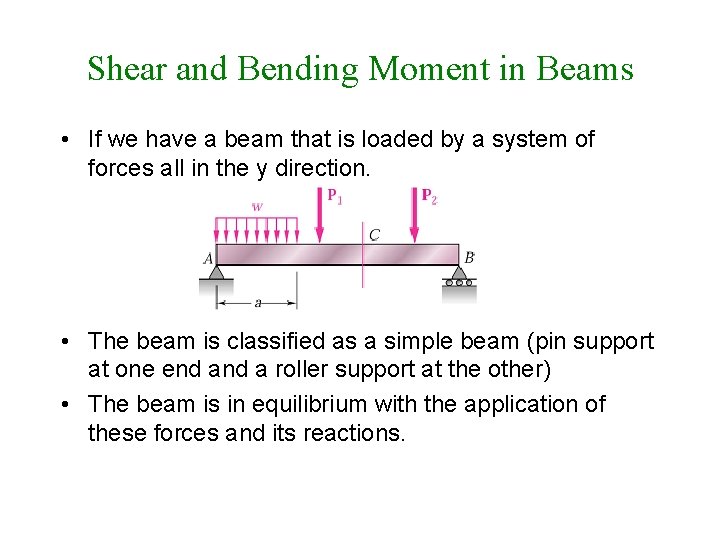
Shear and Bending Moment in Beams • If we have a beam that is loaded by a system of forces all in the y direction. • The beam is classified as a simple beam (pin support at one end a roller support at the other) • The beam is in equilibrium with the application of these forces and its reactions.

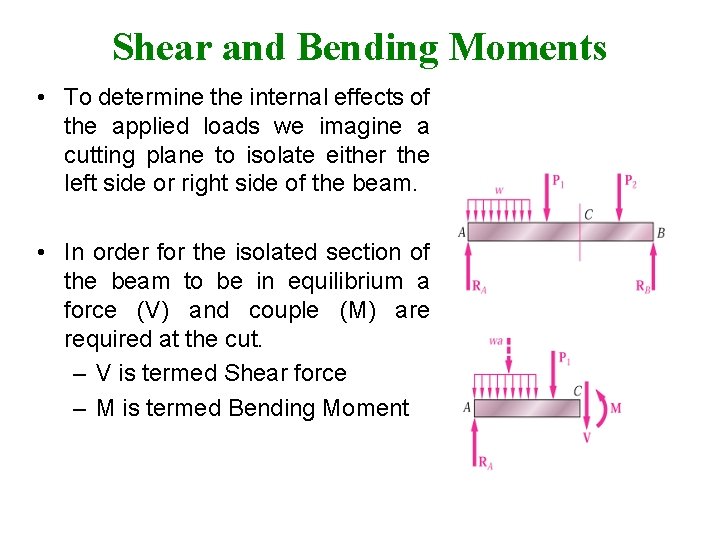
Shear and Bending Moments • To determine the internal effects of the applied loads we imagine a cutting plane to isolate either the left side or right side of the beam. • In order for the isolated section of the beam to be in equilibrium a force (V) and couple (M) are required at the cut. – V is termed Shear force – M is termed Bending Moment

Shear and Bending Moments • The shear V and Moment M are the force and couple applied to the left part of the beam by the right side of the beam to maintain equilibrium. • Equilibrium of both sides is required because the entire beam is in equilibrium. • The section can be made anywhere along the length of the beam. • Shear and Moment are a function of the distance from the origin.

Shear Forces, Bending Moments Sign Conventions Shear forces: positive shear: negative shear: Bending moments: positive moment negative moment left section right section

Shear Forces, Bending Moments Sign Conventions The signs associated with the shear force and bending moment are defined in a different manner than the signs associated with forces and moments in static equilibrium. + shear + moment • The Shear Force is positive if it tends to rotate the beam section clockwise with respect to a point inside the beam section. • The Bending Moment is positive if it tends to bend the beam section concave facing upward. (Or if it tends to put the top of the beam into compression and the bottom of the beam into tension. )

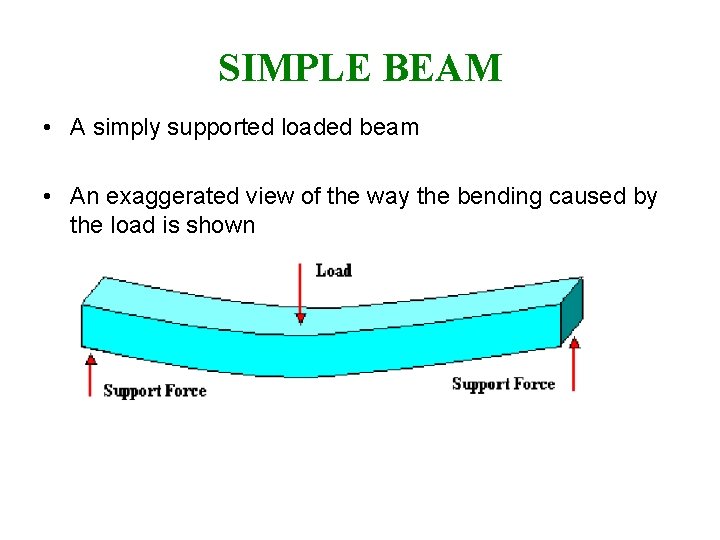
SIMPLE BEAM • A simply supported loaded beam • An exaggerated view of the way the bending caused by the load is shown

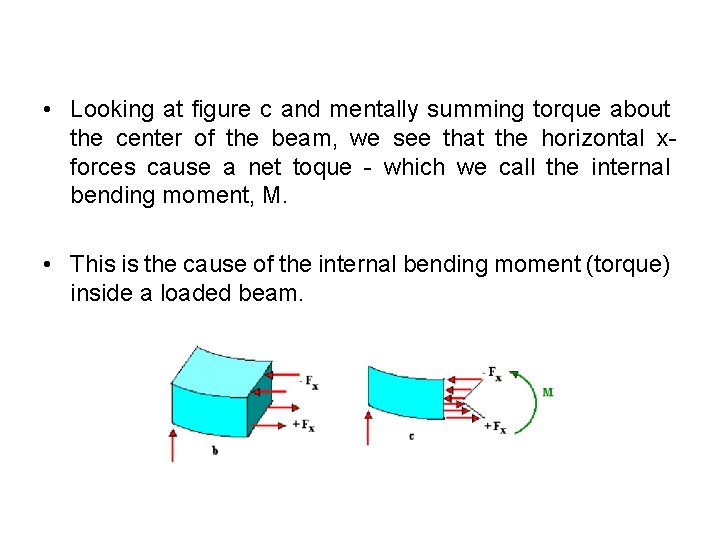
• Looking at figure c and mentally summing torque about the center of the beam, we see that the horizontal xforces cause a net toque - which we call the internal bending moment, M. • This is the cause of the internal bending moment (torque) inside a loaded beam.

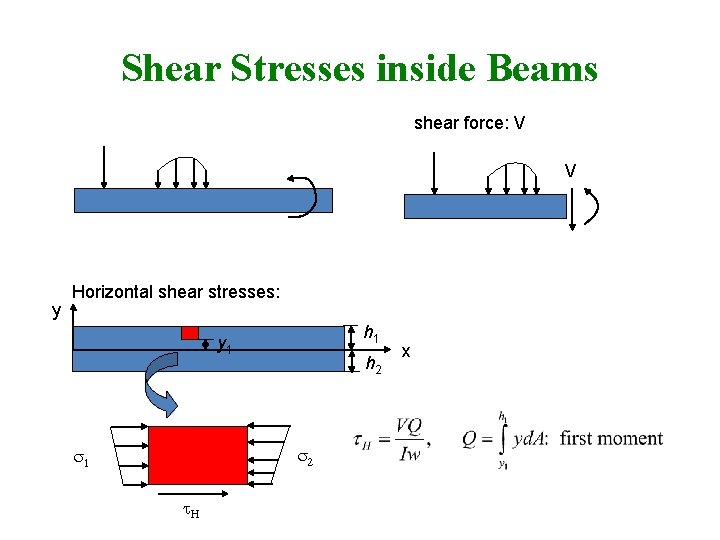
Shear Stresses inside Beams shear force: V V y Horizontal shear stresses: h 1 y 1 h 2 s 1 t. H x

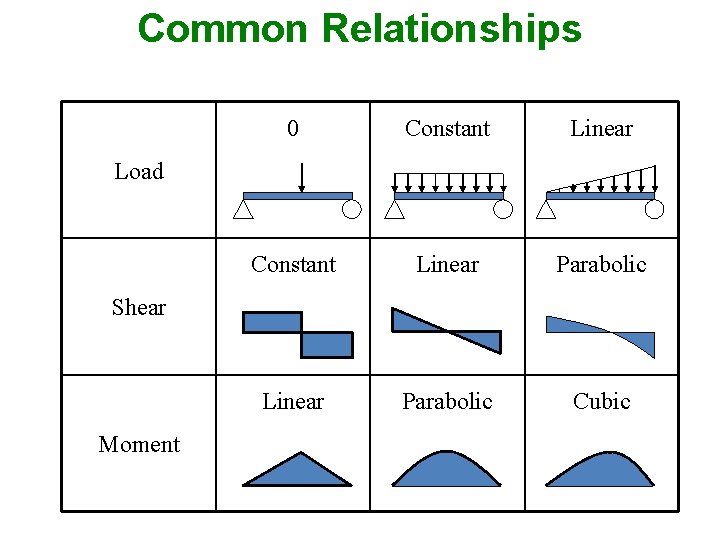
Common Relationships 0 Constant Linear Parabolic Cubic Load Shear Moment

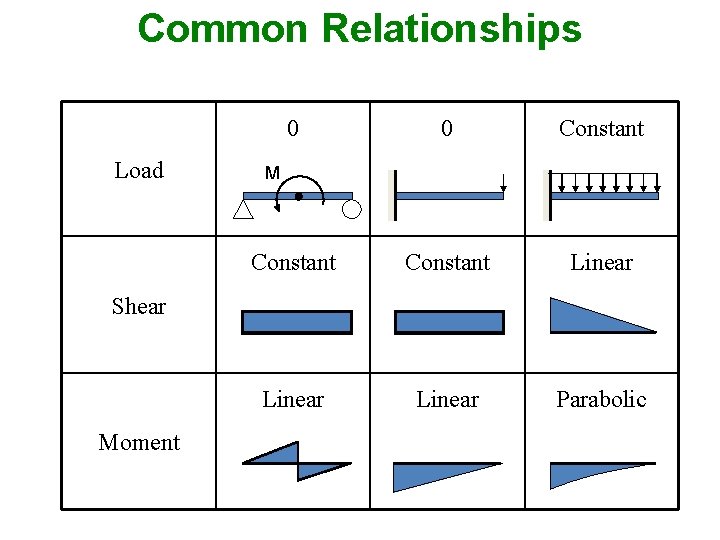
Common Relationships Load 0 0 Constant Linear Parabolic M Shear Moment