Street Generation for City Modeling Xavier Dcoret Franois

Street Generation for City Modeling Xavier Décoret, François Sillion i. MAGIS GRAVIR/IMAG - INRIA 1

Foreword ü A Computer Graphics point of view – Graphic artists – Game developers – Researchers ü A work in 2 parts – A framework – An algorithm 2

Motivations ü City Modeling is a growing field of interest – Game and Leisure » Virtual environments are widely used » Need for larger environments » Cities are natural and appealing large environments – Analysis and Simulation » Pedestrians or traffic flow » Wave transportation 3

Motivations ü Creating the virtual model is a tedious task – Realistic model » Model it by hand: long and costly » Reconstruct it automatically: not working yet – Semi-realistic model » Procedural modelling » Map is exact, geometry is approximative 4

Motivations ü Creating the virtual model is a tedious task – Realistic model » Model it by hand: long and costly » Reconstruct it automatically: not working yet – Semi-realistic model » Procedural modelling » Map is exact, geometry is approximative No existing tool 5

Overview of the tool ü Retrieve the 2 D footprints of buildings – Aerial photographs – Existing 2 D models ü Procedurally generate buildings – Grammar, library of shapes – Style information provided by a designer (GIS) ü Generate streets – Retrieve the street network – Generate geometry 6

Overview of the tool ü Retrieve the 2 D footprints of buildings – Aerial photographs – Existing 2 D models ü Procedurally generate buildings – Grammar, library of shapes – Style information provided by a designer (GIS) ü Generate streets – Retrieve the street network – Generate geometry Our contribution 7

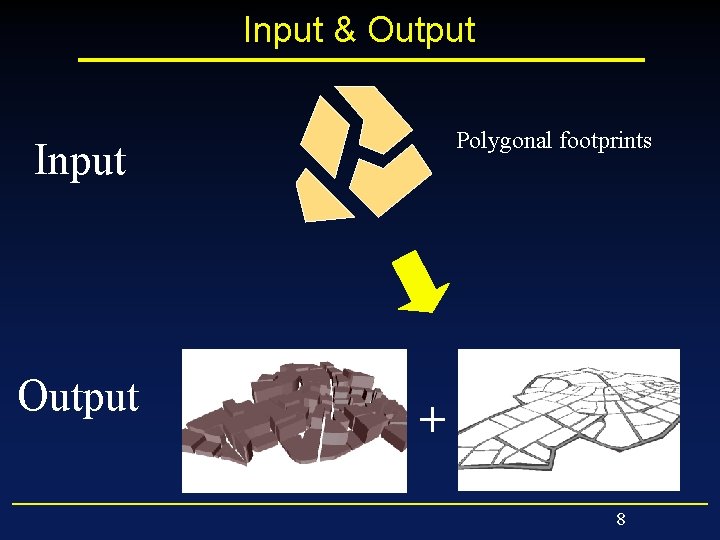
Input & Output Polygonal footprints Input Output + 8

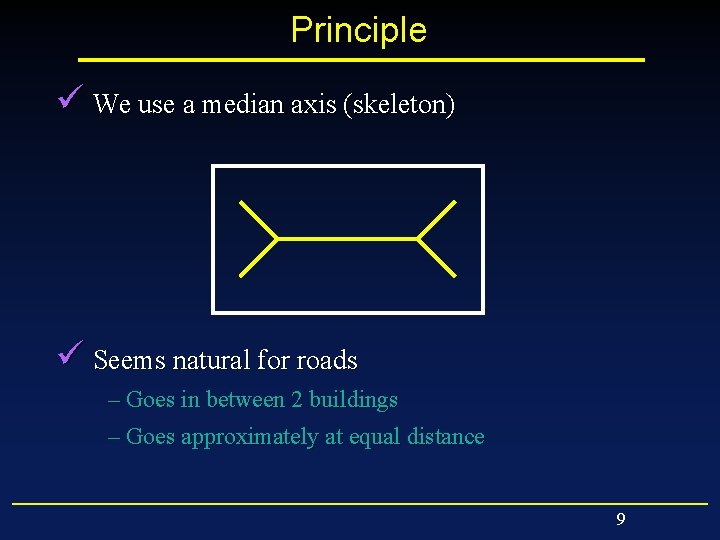
Principle ü We use a median axis (skeleton) ü Seems natural for roads – Goes in between 2 buildings – Goes approximately at equal distance 9

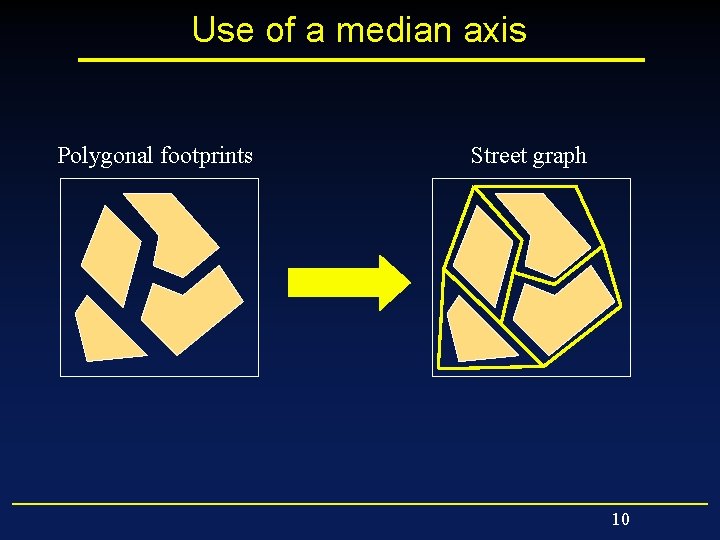
Use of a median axis Polygonal footprints Street graph 10

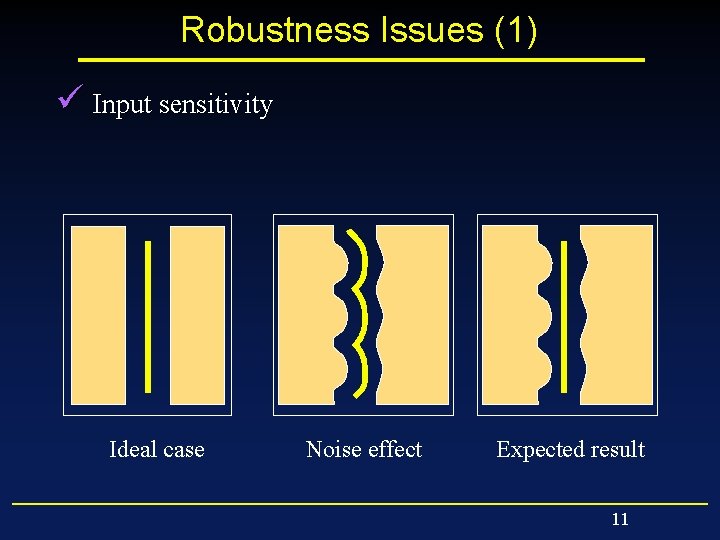
Robustness Issues (1) ü Input sensitivity Ideal case Noise effect Expected result 11

Robustness Issues (2) ü Artefacts Unwanted branches requiring post-processing 12

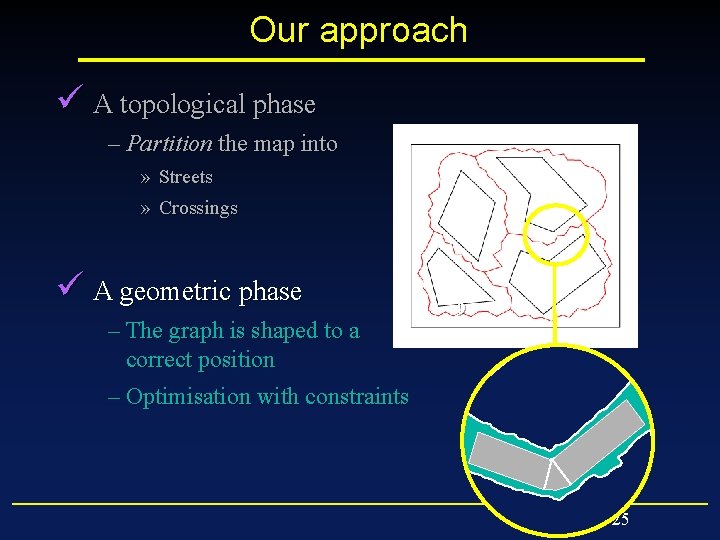
Our approach ü A topological phase – Partition the map into » Streets » Crossings 13

Our approach ü A topological phase – Partition the map into » Streets » Crossings 14

Our approach ü A topological phase – Partition the map into » Streets » Crossings 1 2 5 7 9 4 6 8 3 15

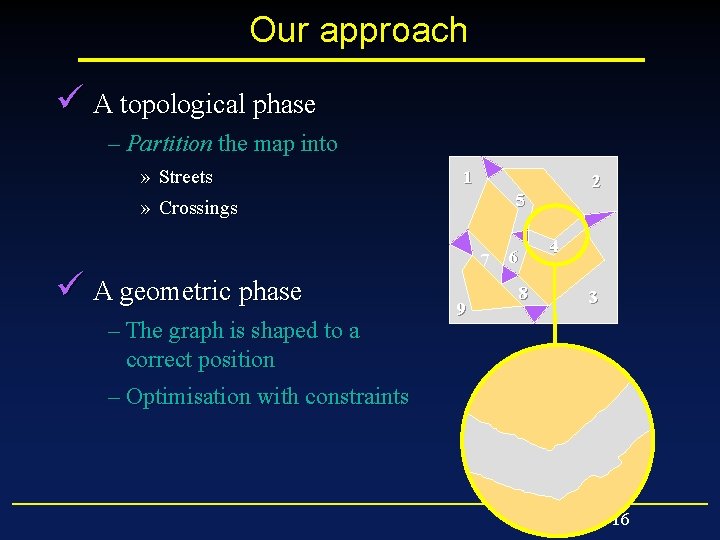
Our approach ü A topological phase – Partition the map into » Streets » Crossings ü A geometric phase – The graph is shaped to a correct position – Optimisation with constraints 1 2 5 7 9 4 6 8 3 16

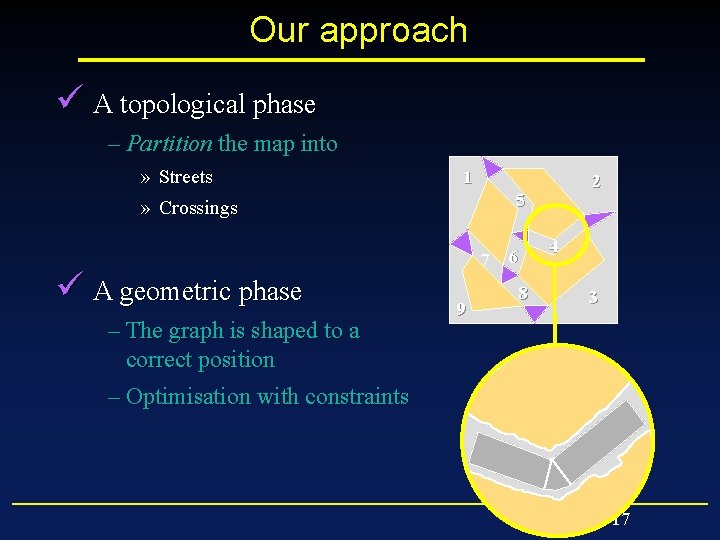
Our approach ü A topological phase – Partition the map into » Streets » Crossings ü A geometric phase – The graph is shaped to a correct position – Optimisation with constraints 1 2 5 7 9 4 6 8 3 17

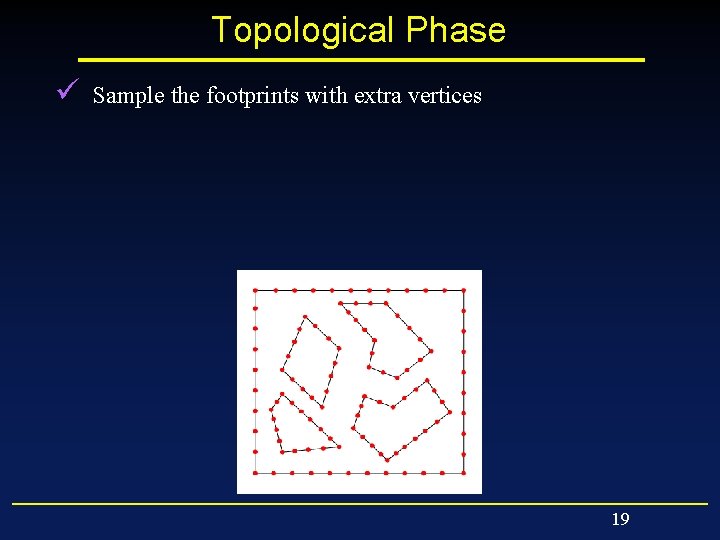
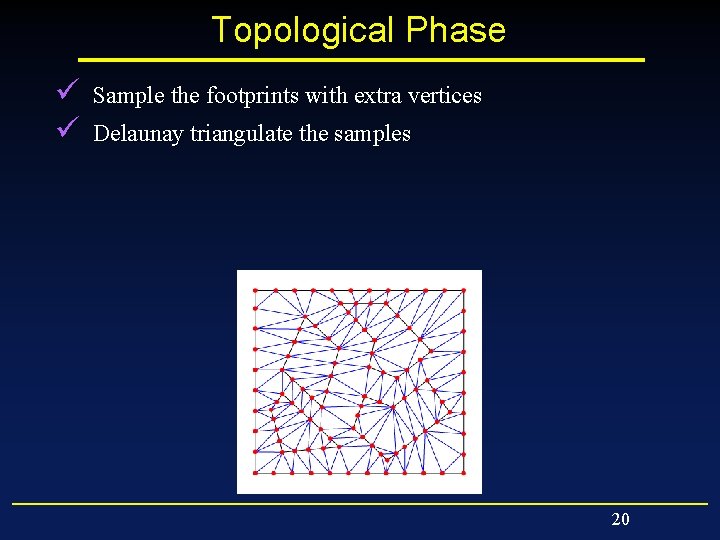
Topological Phase ü Sample the footprints with extra vertices 18

Topological Phase ü Sample the footprints with extra vertices 19

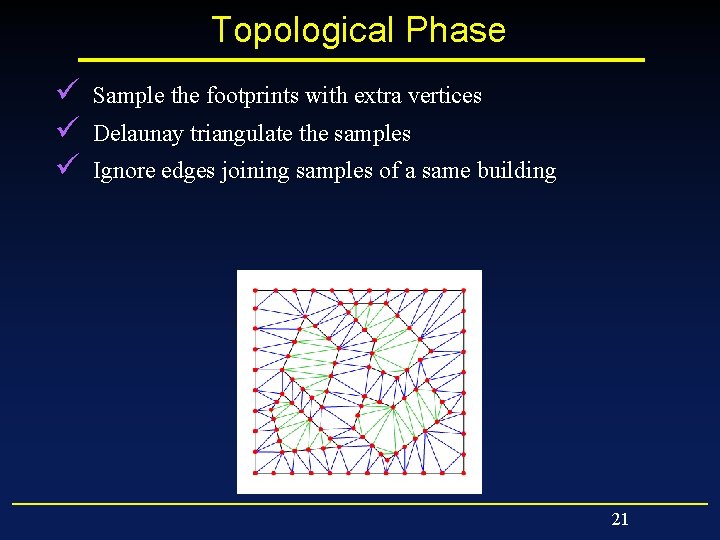
Topological Phase ü ü Sample the footprints with extra vertices Delaunay triangulate the samples 20

Topological Phase ü ü ü Sample the footprints with extra vertices Delaunay triangulate the samples Ignore edges joining samples of a same building 21

Topological Phase ü ü ü Sample the footprints with extra vertices Delaunay triangulate the samples Ignore edges joining samples of a same building 22

Topological Phase ü ü Sample the footprints with extra vertices Delaunay triangulate the samples Ignore edges joining samples of a same building Take the dual of edges (Voronoï diagram) 23

Topological Phase ü ü ü Sample the footprints with extra vertices Delaunay triangulate the samples Ignore edges joining samples of a same building Take the dual of edges (Voronoï diagram) Construct a graph from the edges Crossings Streets 24

Our approach ü A topological phase – Partition the map into » Streets » Crossings ü A geometric phase – The graph is shaped to a correct position – Optimisation with constraints 9 25

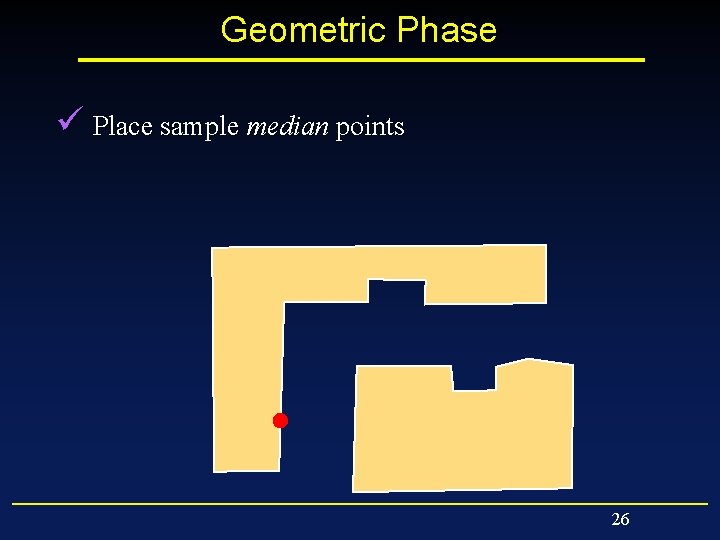
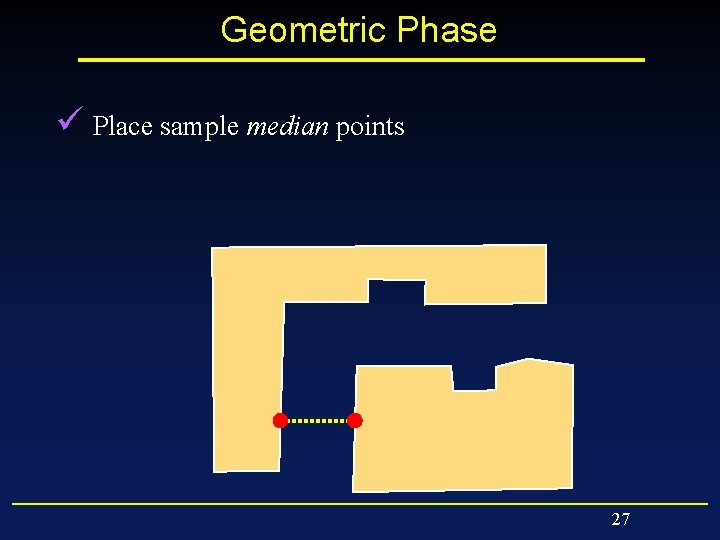
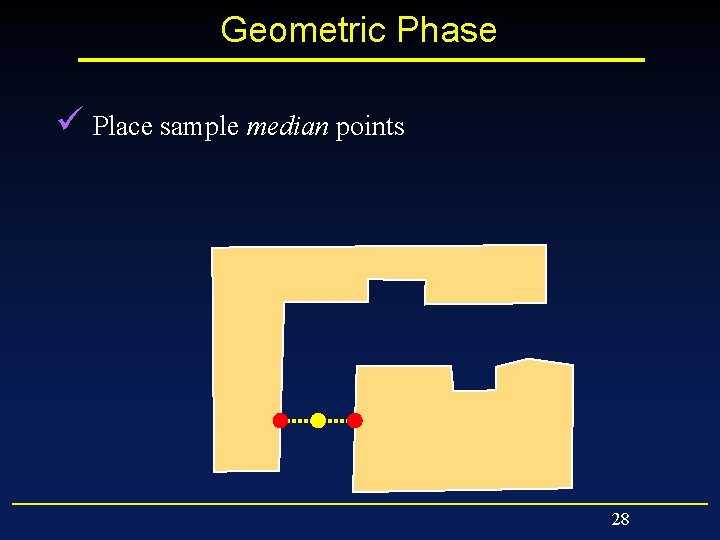
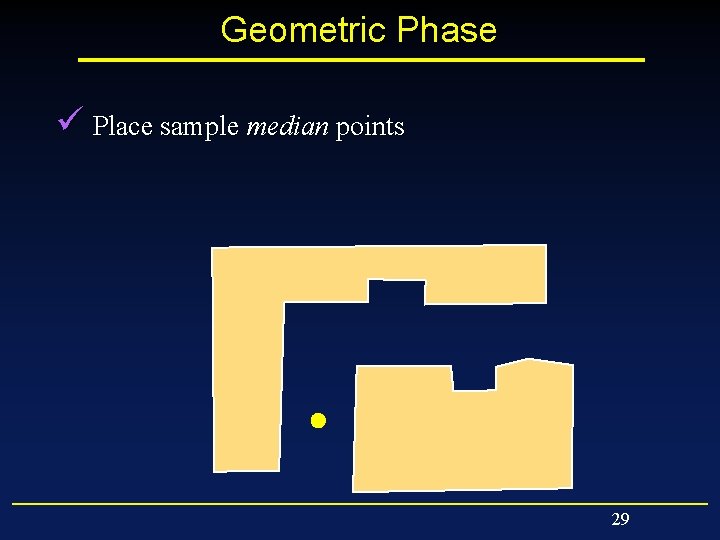
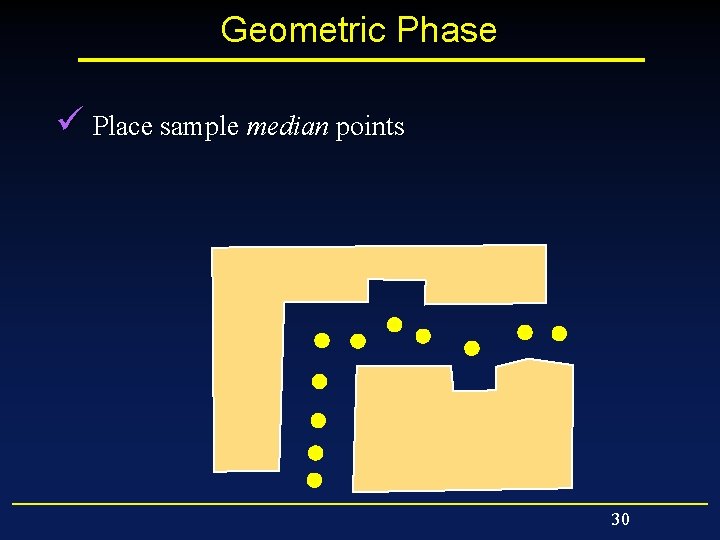
Geometric Phase ü Place sample median points 26

Geometric Phase ü Place sample median points 27

Geometric Phase ü Place sample median points 28

Geometric Phase ü Place sample median points 29

Geometric Phase ü Place sample median points 30

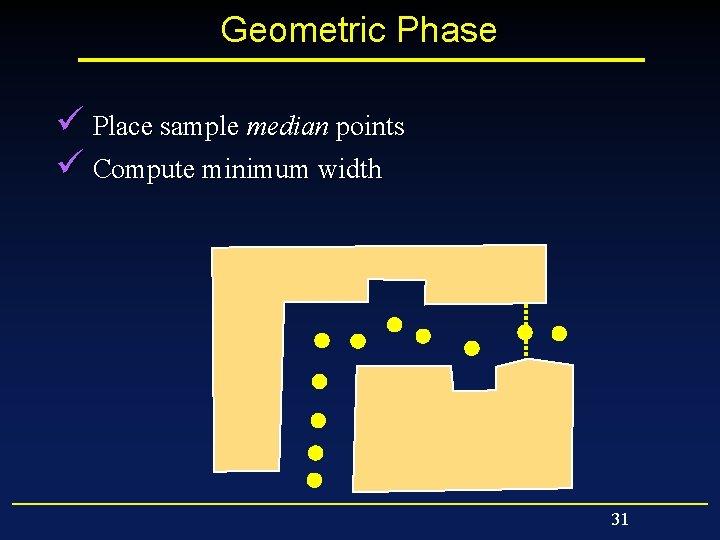
Geometric Phase ü Place sample median points ü Compute minimum width 31

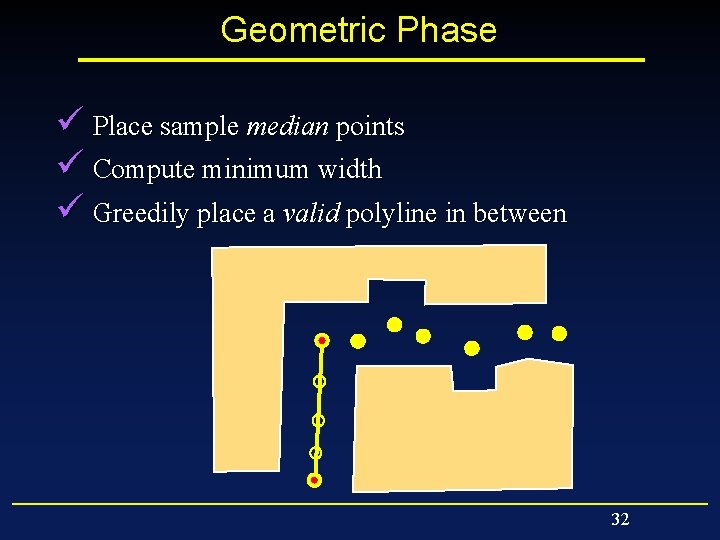
Geometric Phase ü Place sample median points ü Compute minimum width ü Greedily place a valid polyline in between 32

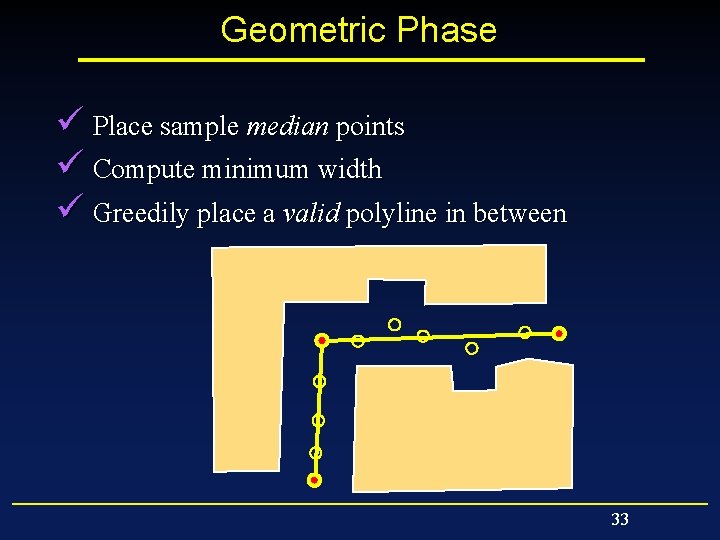
Geometric Phase ü Place sample median points ü Compute minimum width ü Greedily place a valid polyline in between 33

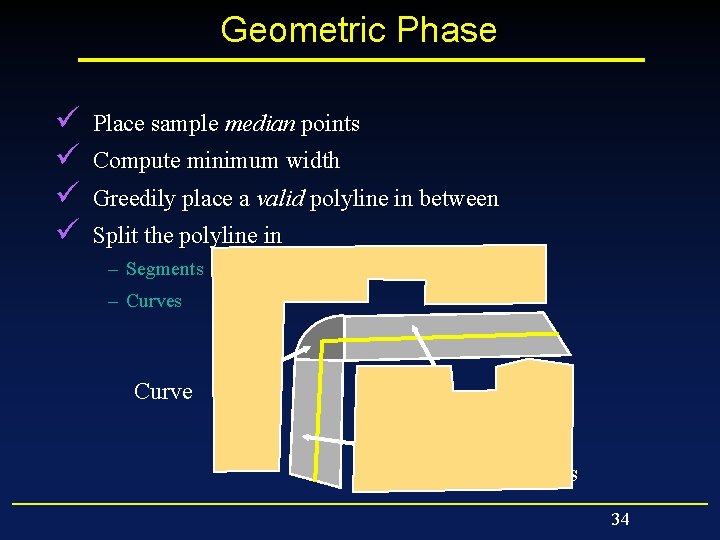
Geometric Phase ü ü Place sample median points Compute minimum width Greedily place a valid polyline in between Split the polyline in – Segments – Curves Curve Segments 34

Robustness ü A topological phase – Partition the map into » Streets » Crossings - Based on distance - Robust to footprints’shape - Solves input sensitivity ü A geometric phase – The graph is shaped to a correct position – Optimisation with constraints - Based on optimisation - Robust to footprints’shape - Solves artefacts 35

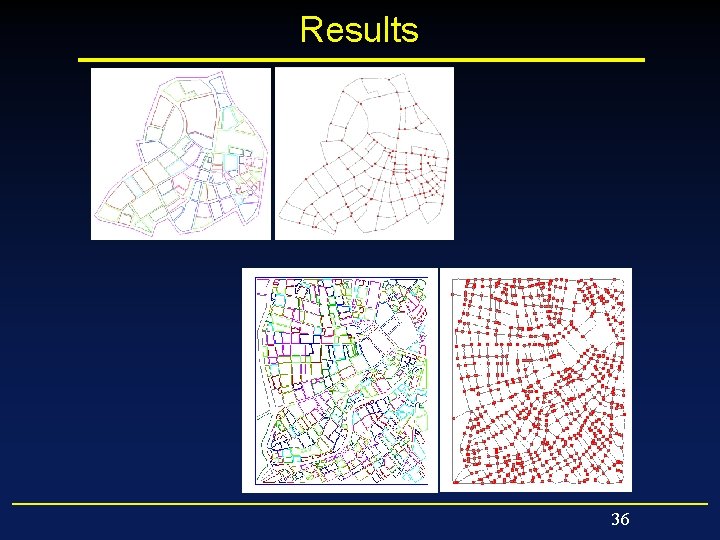
Results 36

Street Generation ü Generate streets – Retrieve the street network » Topology » Simple primitives – Generate geometry » Match buildings boundaries » Connect correctly at crossings 37

Workflow ü Generate streets – Retrieve the street network » Topology » Simple primitives – Generate geometry » Match buildings boundaries » Connect correctly at crossings 38

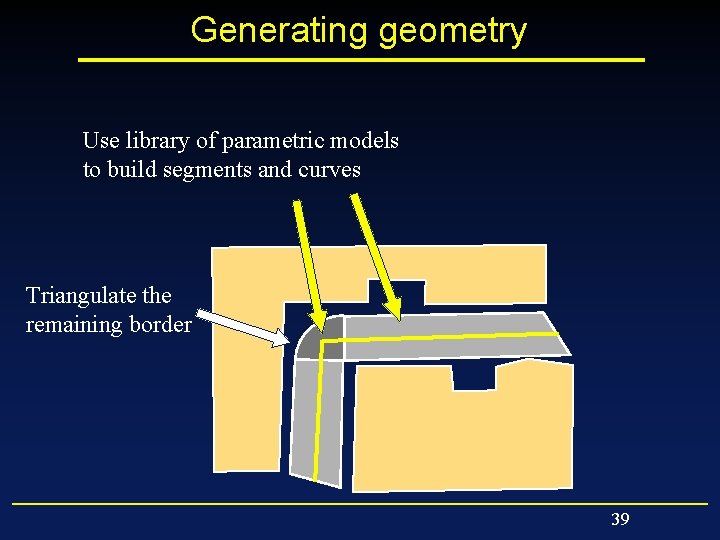
Generating geometry Use library of parametric models to build segments and curves Triangulate the remaining border 39

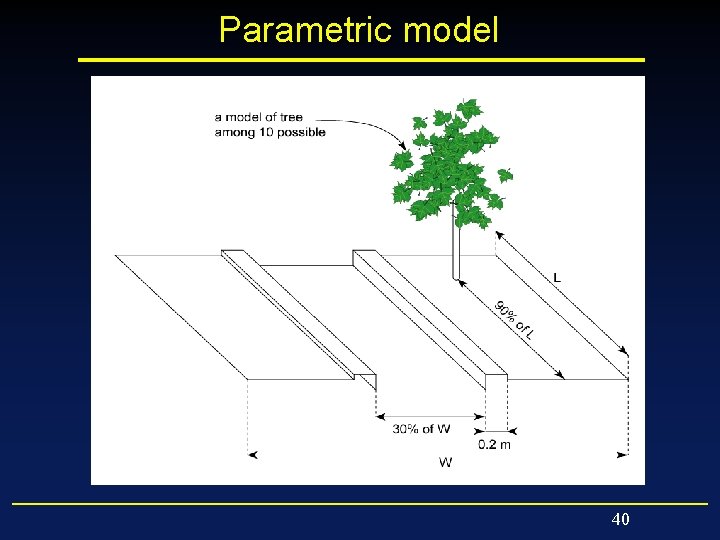
Parametric model 40

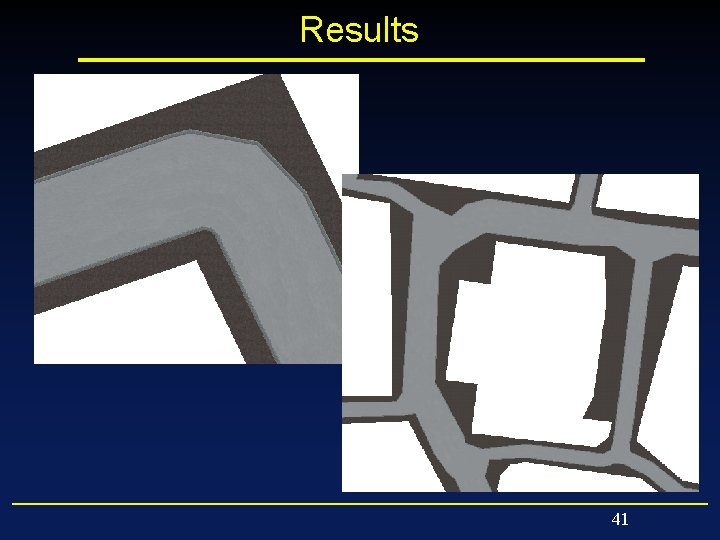
Results 41

Conclusion & Future Works ü We can generate geometry from a 2 D map of buildings – Work in 2 D 1/2 ü Write more parametric modules ü High level features extractions – Avenues – Squares ü Generate coherent trafic signs 42