Stream Function Velocity Potential n Stream lines Stream

Stream Function & Velocity Potential n Stream lines/ Stream Function (Y) u Concept u Relevant Formulas u Examples u Rotation, vorticity n Velocity Potential(f) u Concept u Relevant Formulas u Examples u Relationship between stream function and velocity potential u Complex velocity potential

Stream Lines n n Consider 2 D incompressible flow Continuity Eqn Vx and Vy are related Can you write a common function for both?

Stream Function Assume n n Then n n Instead of two functions, Vx and Vy, we need to solve for only one function y - Stream Function Order of differential eqn increased by one

Stream Function n What does Stream Function y mean? n Equation for streamlines in 2 D are given by y = constant n Streamlines may exist in 3 D also, but stream function does not u Why? (When we work with velocity potential, we may get a perspective) u In 3 D, streamlines follow the equation

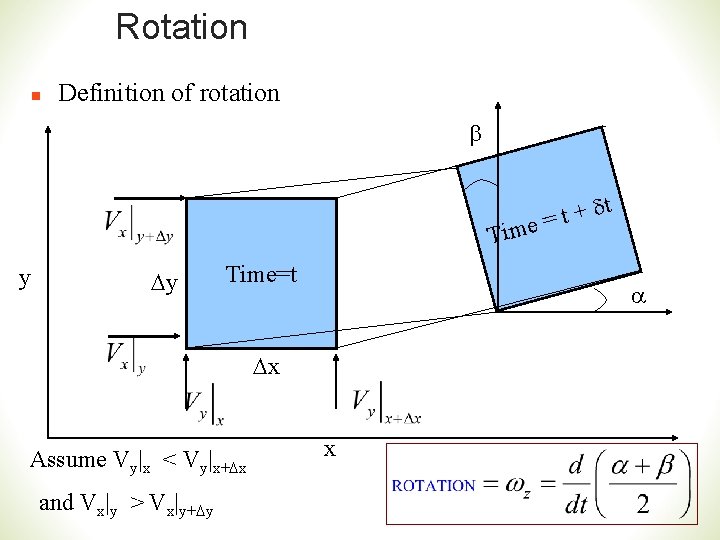
Rotation n Definition of rotation b dt + t e= Tim y Dy Time=t a Dx Assume Vy|x < Vy|x+Dx and Vx|y > Vx|y+Dy x

Rotation n To Calculate Rotation dt + t e= Tim a Dx n Similarly Dy 1

Rotation n To Calculate Rotation a n For very small time and very small element, Dx, Dy and Dt are close to zero b

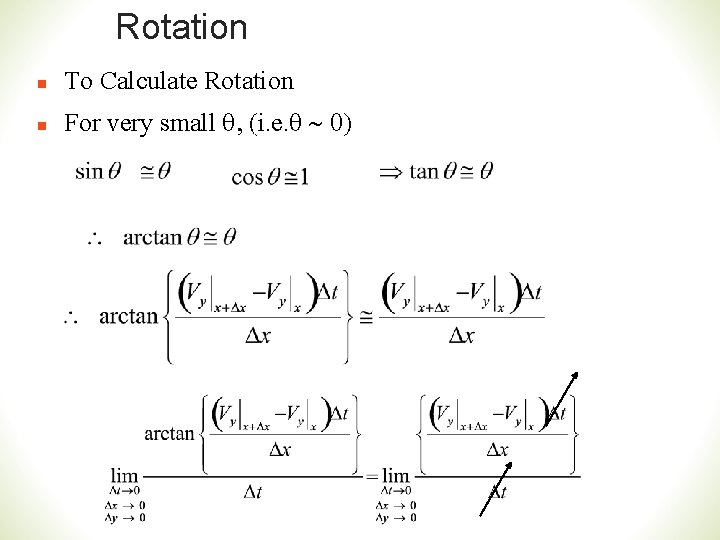
Rotation n To Calculate Rotation n For very small q, (i. e. q ~ 0)

Rotation n To Calculate Rotation Simplifies to

n Rotation in terms of Stream Function To write rotation in terms of stream functions, Assume that ψ is a stream function. So n n That is For irrotational flow (wz=0)

Stream Function- Physical meaning n Statement: In n Proof n If y = constant, then dy=0 n 2 D (viscous or inviscid) flow (incompressible flow OR steady state compressible flow), y = constant represents the streamline. Vy If y = constant, then Vx