Stream Function Definitions For Confined Aquifer Discharge Potential


















- Slides: 19

Stream Function Definitions For Confined Aquifer Discharge Potential Then U is aquifer flux. It is a vector. U = qb, where q is flux per unit depth and b is aquifer thickness

Governing Equations Continuity Equation becomes Zero Divergence implies no sources or sinks Get La. Place Equation by substitution into above Solutions to La. Place equation are potential functions. When Divergence of a vector field is zero, flux is the gradient of the potential.

Unconfined Aquifer (redefine T) Base of Aquifer is datum, H is saturated thickness. T=KH.

Potentials are Constant Heads Because , gradient of potential field gives aquifer flux. Lines along which potential is constant are called Equipotential lines, and are like elevation contours. Darcy velocity may be calculated from the aquifer flux U. b is the aquifer thickness for a confined aquifer. Substituting for U and H. For an Unconfined Aquifer

Parallel Vectors In both cases (confined, unconfined) the following vector fields are parallel Note: v is the seepage velocity v = q/n, where n is porosity Since the divergence is zero, the streamlines cannot cross or join. U is convenient, since its formulation is the same for confined and unconfined aquifers.

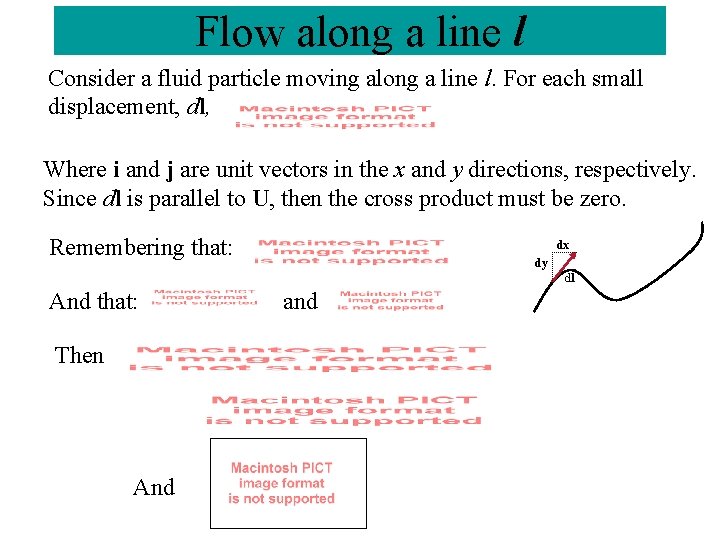
Flow along a line l Consider a fluid particle moving along a line l. For each small displacement, dl, Where i and j are unit vectors in the x and y directions, respectively. Since dl is parallel to U, then the cross product must be zero. Remembering that: dx dy dl And that: Then And and

Stream Function Since must be satisfied along a line l, such a line is called a streamline or flow line. A mathematical construct called a stream function can describe flow associated with these lines. The Stream Function is defined as the function which is constant along a streamline, much as a potential function is constant along an equipotential line. Since is constant along a flow line, then for any dl, Along the streamline

Stream Functions Rearranging: we get and from which we can see that So that if one can find the stream function, one can get the discharge by differentiation.

Interpreting Stream Functions l Any Line l is an arbitrary line t is tangent to l n is normal to l t Flow Line 2 n Flow Line 1 What is the flow that crosses l between Flow Lines 1 and 2? For each increment dl:

Discharge Between Lines 1, 2 If we integrate along line l, between Flow Lines 1 and 2 we will get the total flow across the line. This is true even if K or T is heterogeneous

Conjugate Functions We have already shown that: and since The rotation of the discharge potential field may be calculated via the Curl as follows: Since the Curl of U is zero, the flow field is irrotational.

Conjugate Functions Since the Curl of U is zero, the flow field is irrotational. Doing the same calculation, but using the relationship between the Stream Function and U, we get:

Conjugate Functions From this, we see that U is irrotational. , because we know that Thus, the Potential Function and Stream Function both satisfy La. Place’s Equation. By definition, flow lines are parallel to streamlines (lines of constant stream function value), and perpendicular to lines of constant potential. Thus, the streamlines and potential lines are also perpendicular.

Superposition One special property of solutions to the La. Place Equation is that it is linear. Thus, solutions to the equation may be added together, and the sum of solutions will also be a solution. If and Then This implies that if one can find a solution for uniform flow and for a point source or sink, then they can be added together to get a solution for (uniform flow) + (source) + (sink)

Main Equations - Aquifer Flux In Cartesian Coordinates: In Polar Coordinates: These are the Cauchy-Riemann Equations.

Uniform Flow For a uniform flow rate U (L 2/T) at an angle a with respect to the x-axis: a

Radial Flow Source For an injection well at the origin, flow Q across any circle with radius r is equal to due to continuity. Circumference=2 pr U = Flow per unit length There is no rotational flow: r Q

Develop F and Y Lines Separate Integrating Equipotential Streamline

Fand Y Lines for Capture Zone Theory
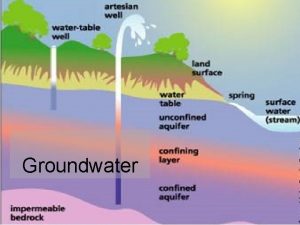
 Unconfined aquifer definition
Unconfined aquifer definition Differentiate byte stream and character stream
Differentiate byte stream and character stream What is the earth's atmosphere made of
What is the earth's atmosphere made of Dockum aquifer
Dockum aquifer Gulf coast aquifer
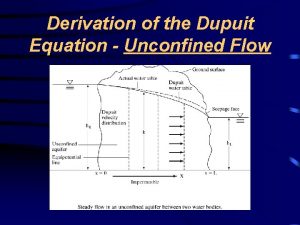
Gulf coast aquifer Dupuit equation is
Dupuit equation is What kind of graph
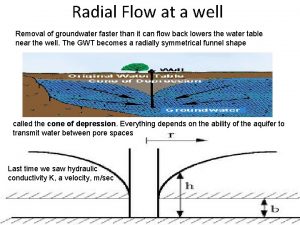
What kind of graph Aquifer well
Aquifer well Ogallala aquifer
Ogallala aquifer Ogallala aquifer
Ogallala aquifer Ogallala aquifer
Ogallala aquifer What is an aquifer
What is an aquifer Aquifer
Aquifer Aquifer lsuhsc
Aquifer lsuhsc How to find pressure potential
How to find pressure potential How to find pressure potential
How to find pressure potential Water potential
Water potential Graded potential vs action potential
Graded potential vs action potential Types of graded potentials
Types of graded potentials Action potential
Action potential