Stream Cipher Introduction Pseudorandomness LFSR Design Refer to

Stream Cipher Introduction Pseudorandomness LFSR Design ü Refer to “Handbook of Applied Cryptography” [Ch 5 & 6] 1

Stream Cipher q Introduction • • ◦ • • • q Originate from one-time pad bit-by-bit Exor with pt and key stream (ci = mi zi) Encryption = Decryption --> Symmetric Use LFSR (Linear Feedback Shift Register) (external) Synchronous or self-synchronous Properties • Faster and Low Complexity in H/W -> Lightweight ! • Security measure : Period of key stream, LC(Linear Complexity), Statistical properties • Vast amounts of theoretical knowledge • Proprietary and Confidential for Military 2

Sequence Def) ◦ s=s 0, s 1, … : infinite seq. , ◦ sn=s 0, s 1, …, sn-1: n term of s ◦ if si = si+n for all i >=0, s is periodic seq. having period n. ◦ run : subsequence of consecutive ‘ 0’(gap) or consecutive ‘ 1’(block) 3

Pseudorandomness 4

Golomb’s postulates(I) s. N : periodic seq. of period N (1) For a cycle of s. N, 0~1 balanceness, i. e, | #{si=1} - #{sj=0} | =<1 (2) For a cycle of s. N, half the runs have length 1, 1/4 have the length 2, …, etc. (3) Autocorrelation* function is two-valued * Measuring similarity between original and t-shifted sequences ** A sequence satisfying them is called Pseudo-Noise(PN) sequence. 5

Golomb’s postulates(II) (Ex) s 15 = 0, 1, 1, 0, 0, 0, 1, 1, 0, 1 (1) #{0} = 7, #{1}=8 (why ? ) (2) 8 runs, 4 runs with length 1 (2 gaps, 2 blocks), 2 runs with length 2 (1 gap, 1 block), 1 run with length 3 (1 gap), 1 run with length 4 (1 block) (3) Autocorrelation function, C(0)=1, C(t)= 1/15 Thus, PN-seq. 6

Statistical Randomness Five Basic Tests ◦ ◦ ◦ Frequency Test (monobit) Serial Test (twobit; Overlapping is allowed) Poker Test (Frequency of m-bit subsequences) Runs Test Autocorrelation Test Others ◦ ◦ Spectral Test Linear Complexity Profile Quadratic Complexity Universal Test 7

Statistical Test by FIPS 140 -1 For a given 20, 000 bit sample seq. (I) monobit test : The number of ‘ 1’=n 1, 9, 654 < n 1 < 10, 346 (2) poker test : m=4, 1. 03 < X 3 < 57. 4 (3) runs test : for length 1 i 6 (4) long run test : no run greater than 34 8

LFSR 9

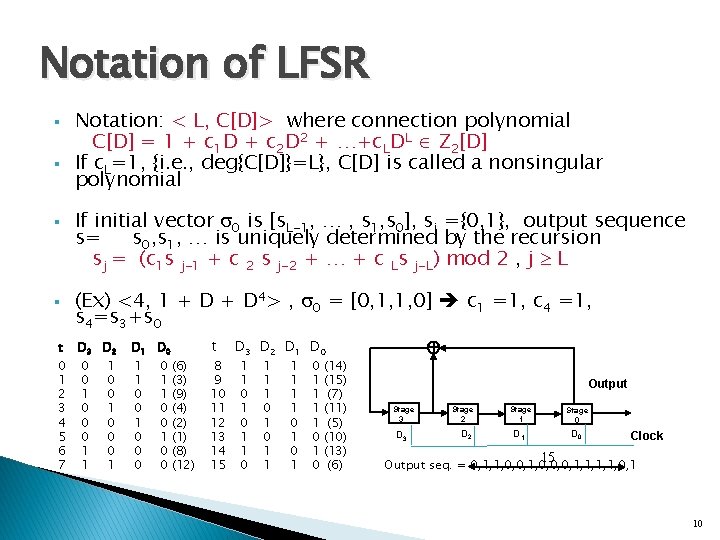
Notation of LFSR § § t 0 1 2 3 4 5 6 7 Notation: < L, C[D]> where connection polynomial C[D] = 1 + c 1 D + c 2 D 2 + …+c. LDL Z 2[D] If c. L=1, {i. e. , deg{C[D]}=L}, C[D] is called a nonsingular polynomial If initial vector 0 is [s. L-1, … , s 1, s 0], si ={0, 1}, output sequence s= s 0, s 1, … is uniquely determined by the recursion sj = (c 1 s j-1 + c 2 s j-2 + … + c Ls j-L) mod 2 , j L (Ex) <4, 1 + D 4> , 0 = [0, 1, 1, 0] c 1 =1, c 4 =1, s 4=s 3+s 0 D 3 D 2 0 0 1 0 0 0 1 1 1 0 0 0 1 D 0 1 1 0 0 0 0 1 1 0 0 (6) (3) (9) (4) (2) (1) (8) (12) t 8 9 10 11 12 13 14 15 D 3 D 2 D 1 D 0 1 1 1 0 1 1 1 0 1 0 (14) (15) (7) (11) (5) (10) (13) (6) Output Stage 3 D 3 Stage 2 D 2 Stage 1 Stage 0 D 1 D 0 Clock 15 Output seq. = 0, 1, 1, 0, 0, 0, 1, 1, 0, 1 10

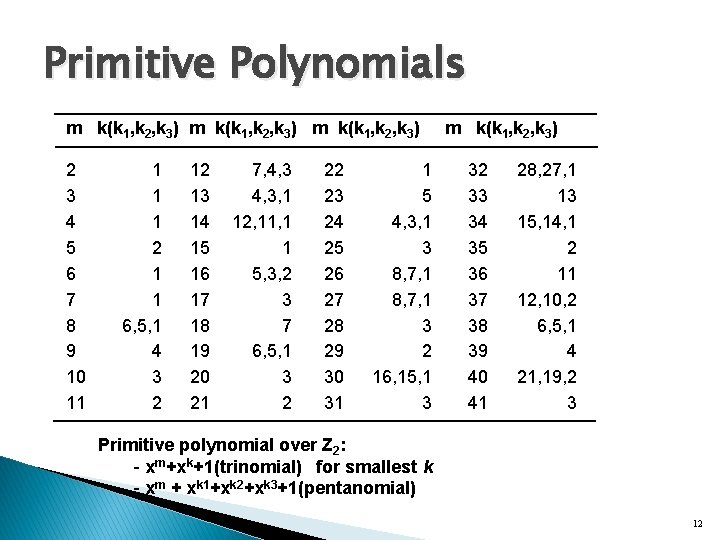
Properties of m-LFSR(I) � The period of the sequence from LFSR divides 2 L-1 �A irreducible polynomial f(x) in Zp[x] of degree m is called a primitive polynomial if and only if f(x) divides xk-1 for k=2 m-1 and for no smaller positive integer k • # of monic primitive poly. of degree m over Zp = (pm-1)/m where is Euler-phi ft. � If the connection polynomial is primitive, the period is 2 L-1 � Such sequence is called Maximum-length Shift Register Seq. , M –seq. and LFSR is called m-LFSR. 11

Primitive Polynomials m k(k 1, k 2, k 3) 2 3 4 5 6 7 8 9 10 11 1 2 1 1 6, 5, 1 4 3 2 12 13 14 15 16 17 18 19 20 21 7, 4, 3, 1 12, 11, 1 1 5, 3, 2 3 7 6, 5, 1 3 2 22 23 24 25 26 27 28 29 30 31 1 5 4, 3, 1 3 8, 7, 1 3 2 16, 15, 1 3 m k(k 1, k 2, k 3) 32 33 34 35 36 37 38 39 40 41 28, 27, 1 13 15, 14, 1 2 11 12, 10, 2 6, 5, 1 4 21, 19, 2 3 Primitive polynomial over Z 2: - xm+xk+1(trinomial) for smallest k - xm + xk 1+xk 2+xk 3+1(pentanomial) 12

Properties of LFSR Well suited for H/W implementation Produce seq. of large period Good statistical properties Readily analyzed by algebraic structure Breakable by consecutive 2 * L subsequence is known to attacker ◦ Using Berlekamp-Massey algorithm, from any (short) subsequences having length at least 2*L, we can find the LFSR with length L 13

Linear Complexity(I) Given an infinite sequence s, the shortest length of LFSR’s that generate s is called Linear � (Def) Complexity � Using Berlekamp-Massey algorithm, LC is computed � (Properties ◦ ◦ ◦ of LC) s, t : binary seq. For any n 1, 0 L(sn) n LC(sn) =0 iff sn is ‘ 0’ seq. of length n. LC(sn) =n iff sn=0, 0, …, 0, 1. If s is periodic with period N, LC(sn) N. LC(s t) LC(s) + LC(t) 14

Linear Complexity(II) sn : random seq. from all seq. of length n Expectation value of LC where B(n)=0 if even n, otherwise 0 For large n, E(L(sn)) n/2 + 2/9 and Var(L(sn)) 86/81 (Def) LCP (Linear Complexity Profile) Denote LN is LC of s. N=s 0, s 1, …s. N-1, L 2, … LN is LCP 15

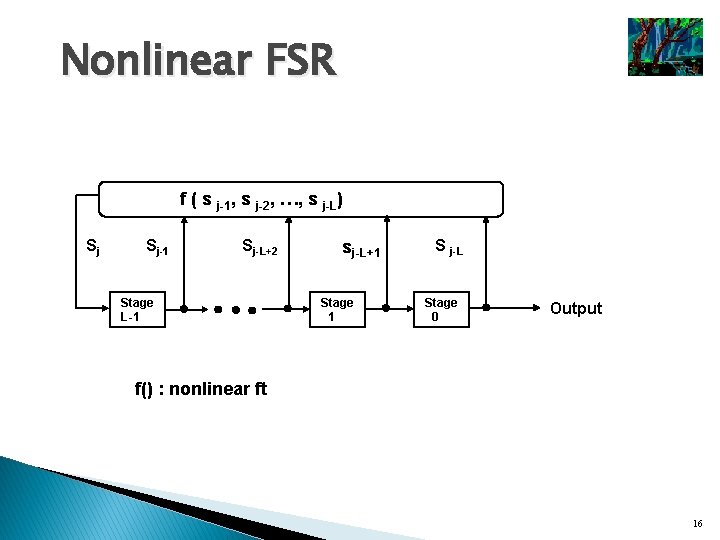
Nonlinear FSR f ( s j-1, s j-2, …, s j-L) Sj Sj-1 Sj-L+2 Stage L-1 sj-L+1 Stage 1 S j-L Stage 0 Output f() : nonlinear ft 16

Design 17

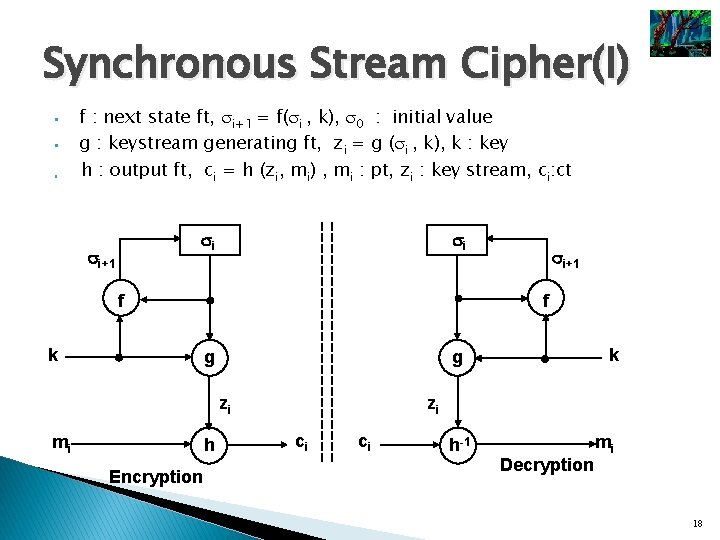
Synchronous Stream Cipher(I) § § § f : next state ft, i+1 = f( i , k), 0 : initial value g : keystream generating ft, zi = g ( i , k), k : key h : output ft, ci = h (zi, mi) , mi : pt, zi : key stream, ci: ct i i+1 i f k f g h Encryption k g zi mi i+1 zi ci ci h-1 Decryption mi 18

Synchronous Stream Cipher(II) Keystream is independent of pt and ct Properties ◦ ◦ ◦ Synchronization requirement No error propagation Active attack Insertion, deletion or replay will lose synchronization Change selected ciphertext digits Need to have integrity check mechanisms 19

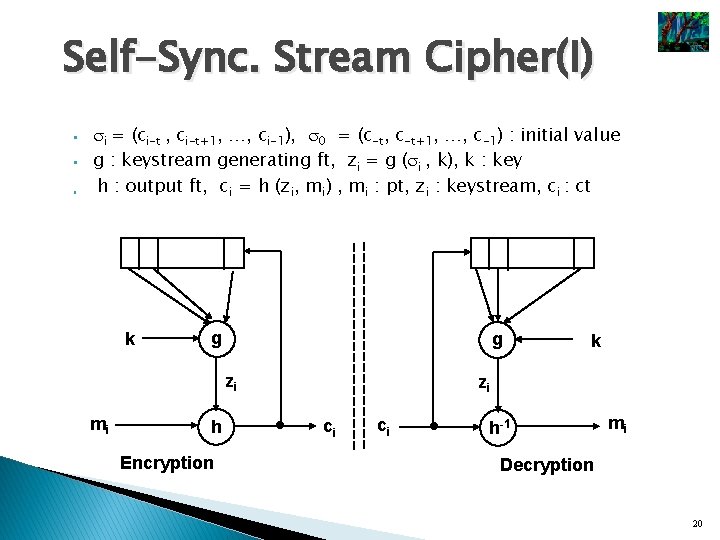
Self-Sync. Stream Cipher(I) § § § i = (ci-t , ci-t+1, …, ci-1), 0 = (c-t, c-t+1, …, c-1) : initial value g : keystream generating ft, zi = g ( i , k), k : key h : output ft, ci = h (zi, mi) , mi : pt, zi : keystream, ci : ct k g g zi mi h Encryption k zi ci ci h-1 mi Decryption 20

Self-Sync. Stream Cipher(II) Keystream is independent of pt and ct Properties ◦ Self-Synchronization ◦ Limited error propagation ◦ Active attack Difficult to detect insertion, deletion, or replay Easy to find passive modification ◦ More diffusion more resistant against attacks based on plaintext redundancy 21

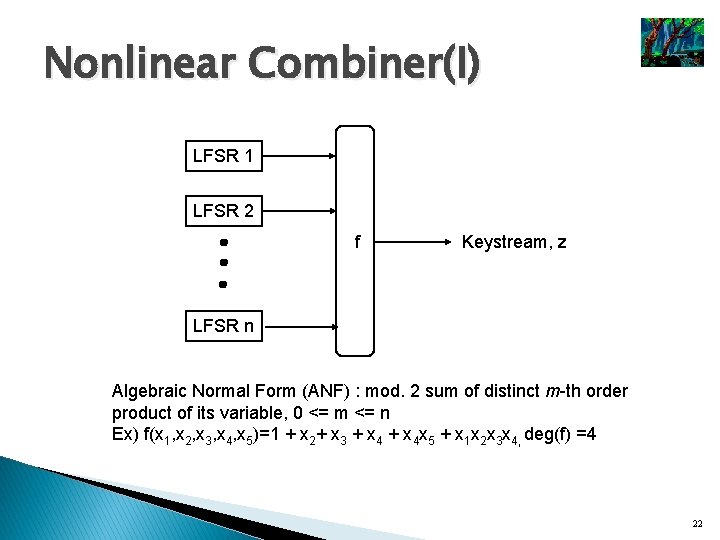
Nonlinear Combiner(I) LFSR 1 LFSR 2 f Keystream, z LFSR n Algebraic Normal Form (ANF) : mod. 2 sum of distinct m-th order product of its variable, 0 <= m <= n Ex) f(x 1, x 2, x 3, x 4, x 5)=1 + x 2+ x 3 + x 4 x 5 + x 1 x 2 x 3 x 4, deg(f) =4 22

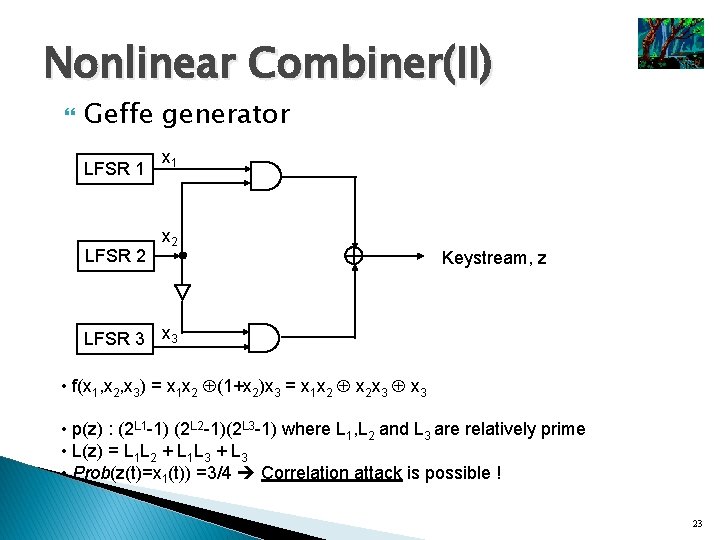
Nonlinear Combiner(II) Geffe generator LFSR 1 LFSR 2 x 1 x 2 Keystream, z LFSR 3 x 3 • f(x 1, x 2, x 3) = x 1 x 2 (1+x 2)x 3 = x 1 x 2 x 2 x 3 • p(z) : (2 L 1 -1) (2 L 2 -1)(2 L 3 -1) where L 1, L 2 and L 3 are relatively prime • L(z) = L 1 L 2 + L 1 L 3 + L 3 • Prob(z(t)=x 1(t)) =3/4 Correlation attack is possible ! 23

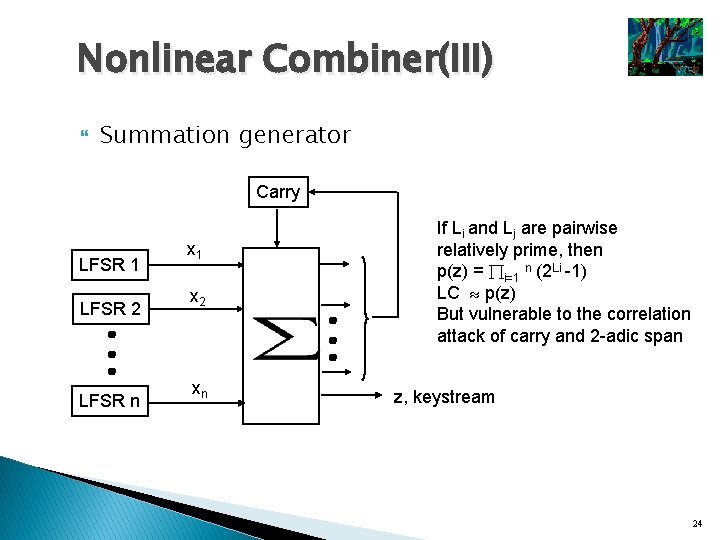
Nonlinear Combiner(III) Summation generator Carry LFSR 1 LFSR 2 LFSR n x 1 x 2 xn If Li and Lj are pairwise relatively prime, then p(z) = i=1 n (2 Li -1) LC p(z) But vulnerable to the correlation attack of carry and 2 -adic span z, keystream 24

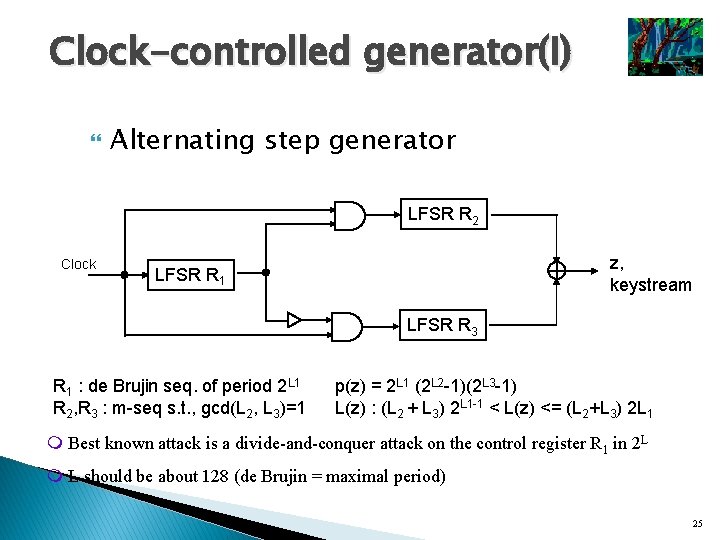
Clock-controlled generator(I) Alternating step generator LFSR R 2 Clock z, keystream LFSR R 1 LFSR R 3 R 1 : de Brujin seq. of period 2 L 1 R 2, R 3 : m-seq s. t. , gcd(L 2, L 3)=1 p(z) = 2 L 1 (2 L 2 -1)(2 L 3 -1) L(z) : (L 2 + L 3) 2 L 1 -1 < L(z) <= (L 2+L 3) 2 L 1 m Best known attack is a divide-and-conquer attack on the control register R 1 in 2 L m L should be about 128 (de Brujin = maximal period) 25

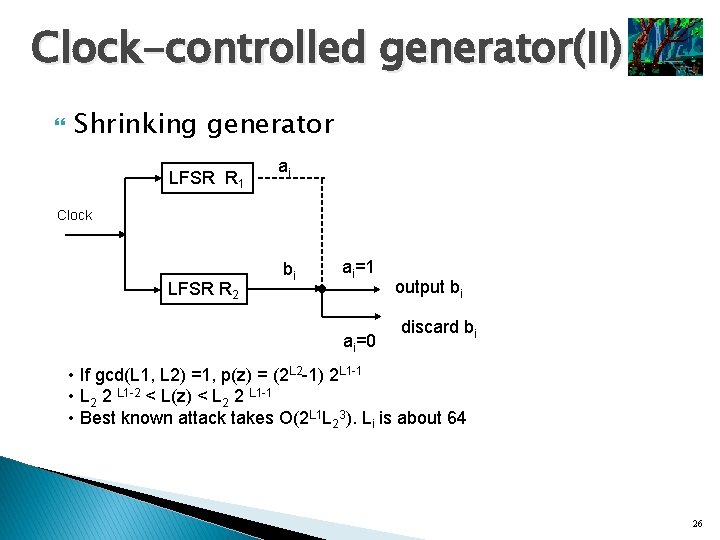
Clock-controlled generator(II) Shrinking generator LFSR R 1 ai Clock LFSR R 2 bi ai=1 ai=0 output bi discard bi • If gcd(L 1, L 2) =1, p(z) = (2 L 2 -1) 2 L 1 -1 • L 2 2 L 1 -2 < L(z) < L 2 2 L 1 -1 • Best known attack takes O(2 L 1 L 23). Li is about 64 26

Other generators Cascade Generator CSPRBG(Cryptographically Secure Pseudo Random Bit Generator) ◦ RSA LSB Generator ◦ BBS Generator (p. 336) Pseudo-noise Generator ◦ Noise Diode or Noise Transistor Feedback with Carry Shift Register (FCSR) ◦ 2 -adic span A 5/1, A 5/2, HC-256, RC 4, PKZIP, Py, Rabbit, FISH, SEAL, Salsa 20, SOBER, etc. 27

Correlation Attack 28

Correlation Attack (I) Siegenthaler, 1984 ◦ The complexity of a Combining Generator depends on the correlation of the combining function F. ◦ Divide-and-Conquer Attack - If the output of F has a correlation with the output of KSG 1, we can find the initial vector of the KSG 1 KSG 2 KSG n x 1 x 2 F z xn 29

Correlation Attack (II) Assume Prob(z=0|xi=0)=1/2 -e, e>0 Identify the initial vector of the KSGi by Divide and Conquer KSG 1 Known ciphertext attack KSG 2 x 1 x 2 Assume an initial vector of KSGi F Generate xi’ from KSGi xn Compute e’=1/2 - Prob(z=0|xi’=0) KSG n If the initial vector is correct, we must have e’=e. If not, we have e 0 since x’ has no correlation with z ◦ This attack is very effective. So e must be zero. ◦ ◦ z 30

Resilient Functions A balanced function {0, 1}m - every possible output m-tuple is equally likely to occur � A k-resilient function f : {0, 1}n {0, 1}m - every possible output m-tuple is equally likely to occur when the values of k arbitrary inputs are fixed and the remaining n-k input bits are chosen independently at random. � A 0 -resilient function is just a balanced function. � A k-resilient function is (k-1)-resilient. � E. g. ) f(x 1, x 2)=x 1+x 2 is 1 -resilient. � 31

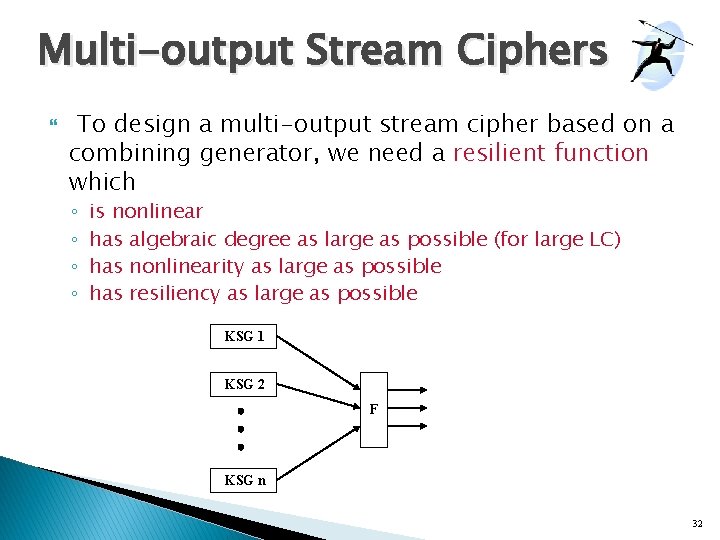
Multi-output Stream Ciphers To design a multi-output stream cipher based on a combining generator, we need a resilient function which ◦ ◦ is nonlinear has algebraic degree as large as possible (for large LC) has nonlinearity as large as possible has resiliency as large as possible KSG 1 KSG 2 F KSG n 32

Summary of a Stream Cipher Period : Depends on req’d level of security Linear Complexity ◦ shortest LFSR that generates a given seq. Measure against Correlation Attack ◦ Correlation Immune function ◦ Nonlinear function 33