Strapdown Inertial Navigation Systems INS Sensors and UAVs

Strapdown Inertial Navigation Systems (INS) Sensors and UAVs Avionic By Dr. Hamid Bolandhemmat

CONTENTS • Overview of Inertial Navigation Systems (INS) and their application • General navigation equations in spaced fixed and rotating reference frames • Inertial sensors • Gyroscopes • Underlying theory • Rebalance loop • Sources of errors • calibration • Accelerometers • Underlying theory • Rebalance loop • Sources of errors • Calibration • Compass • Air data systems • Airspeed • Pressure Altitude • Global Positioning Systems (GPS) • Underlying concept • Pseudo ranges

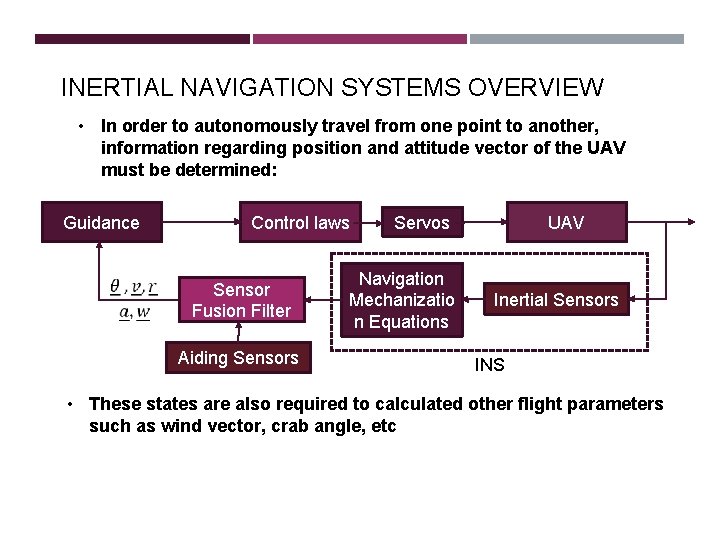
INERTIAL NAVIGATION SYSTEMS OVERVIEW) • In order to autonomously travel from one point to another, information regarding position and attitude vector of the UAV must be determined: Guidance Control laws Sensor Fusion Filter Aiding Sensors Servos Navigation Mechanizatio n Equations UAV Inertial Sensors INS • These states are also required to calculated other flight parameters such as wind vector, crab angle, etc

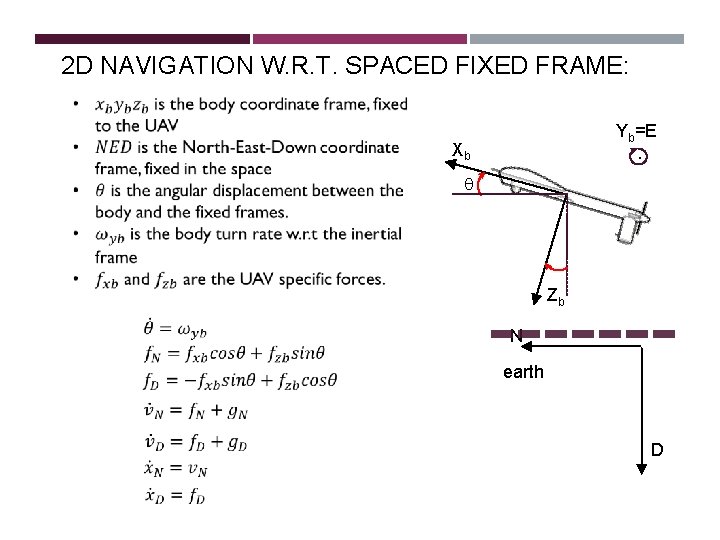
2 D NAVIGATION W. R. T. SPACED FIXED FRAME: Yb=E. Xb q Zb N earth D

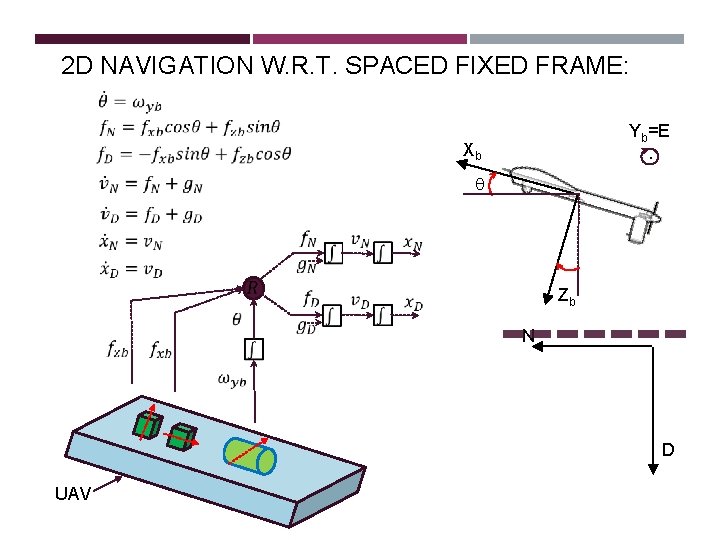
2 D NAVIGATION W. R. T. SPACED FIXED FRAME: Xb q Yb=E. Zb N D UAV

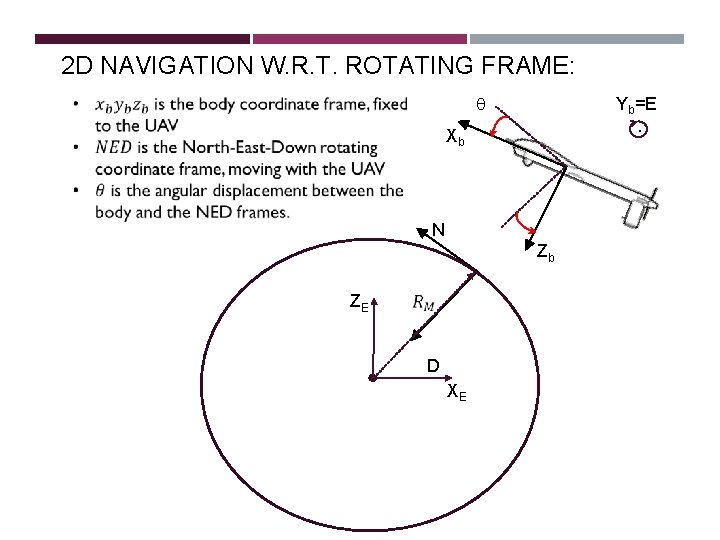
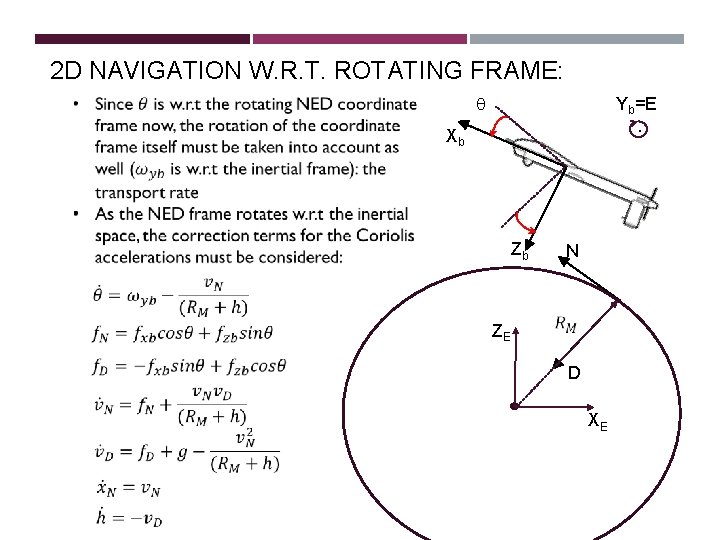
2 D NAVIGATION W. R. T. ROTATING FRAME: q Yb=E. Xb N Zb ZE D XE

2 D NAVIGATION W. R. T. ROTATING FRAME: q Yb=E. Xb Zb N ZE D XE

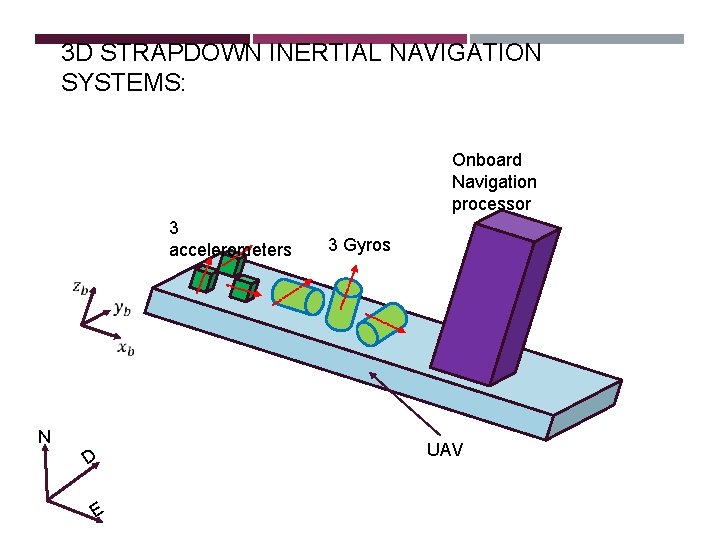
3 D STRAPDOWN INERTIAL NAVIGATION SYSTEMS: Onboard Navigation processor 3 accelerometers 3 Gyros N D E UAV

INERTIAL SENSORS - GYROSCOPES Angular momentum vector

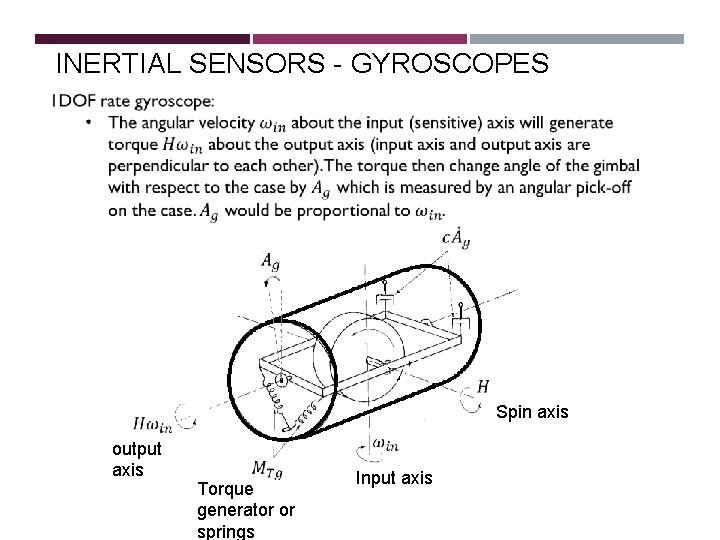
INERTIAL SENSORS - GYROSCOPES • Angular velocity measurement (the application of the precession principle): • The spinning wheel or rotor is put on a gimbal inside an instrument case to be held isolated in space; any changes in the angles of the gimbal then will represent changes in the orientation of the case with respect to the reference direction maintained by the rotor angular momentum

INERTIAL SENSORS - GYROSCOPES output axis Spin axis Torque generator or springs Input axis

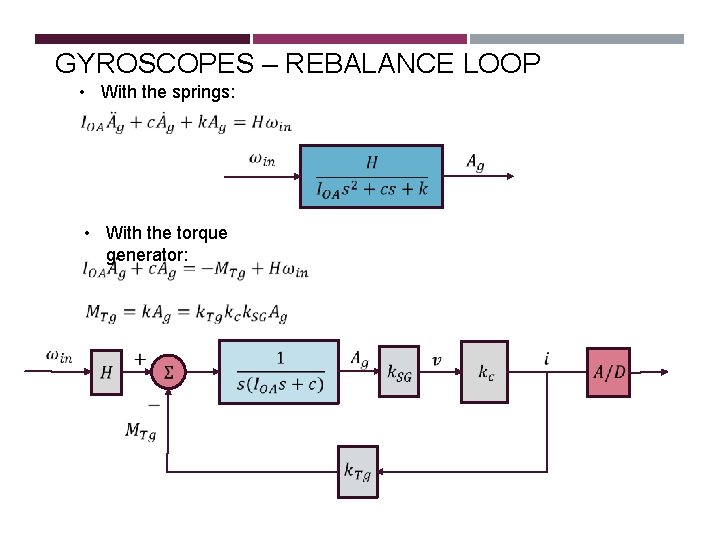
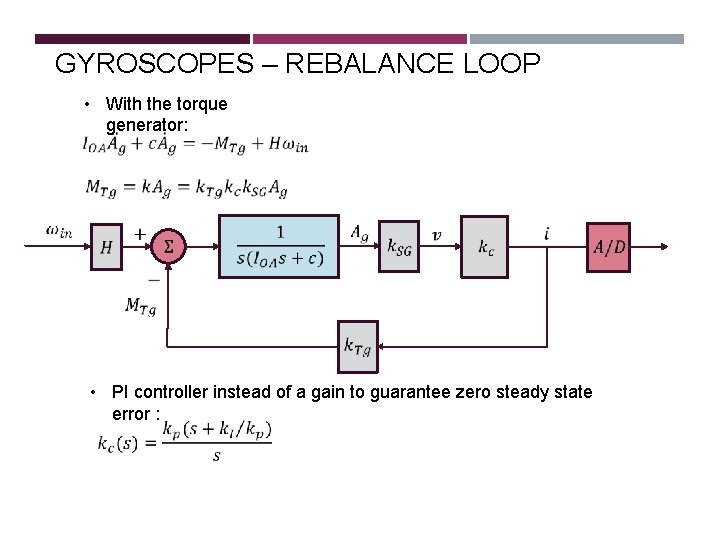
GYROSCOPES – REBALANCE LOOP • With the springs: • With the torque generator:

GYROSCOPES – REBALANCE LOOP • With the torque generator: • PI controller instead of a gain to guarantee zero steady state error :

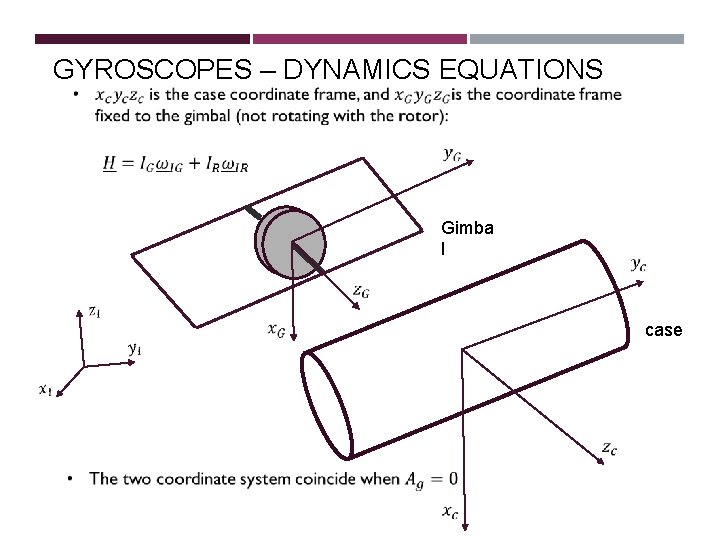
GYROSCOPES – DYNAMICS EQUATIONS Gimba l case

GYROSCOPES – FIBER OPTIC GYROS (FOG): • Underlying principle (Sagnac effect): • The transit time for two counter-propagating beams of light travelling in a fiber optic ring is not the same when the ring is spinning. CCW wave CW wave

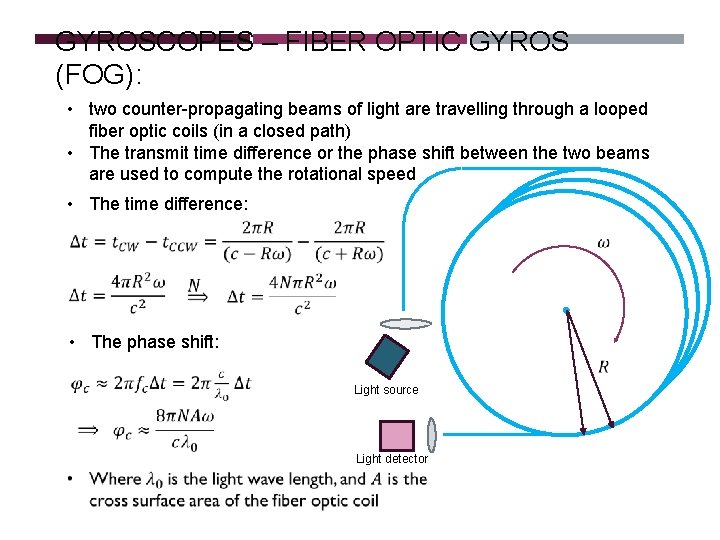
GYROSCOPES – FIBER OPTIC GYROS (FOG): • two counter-propagating beams of light are travelling through a looped fiber optic coils (in a closed path) • The transmit time difference or the phase shift between the two beams are used to compute the rotational speed • The time difference: • The phase shift: Light source Light detector

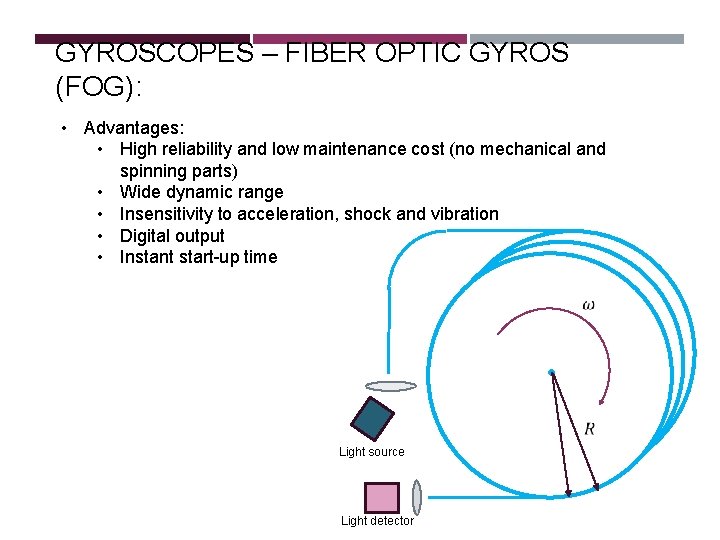
GYROSCOPES – FIBER OPTIC GYROS (FOG): • Advantages: • High reliability and low maintenance cost (no mechanical and spinning parts) • Wide dynamic range • Insensitivity to acceleration, shock and vibration • Digital output • Instant start-up time Light source Light detector

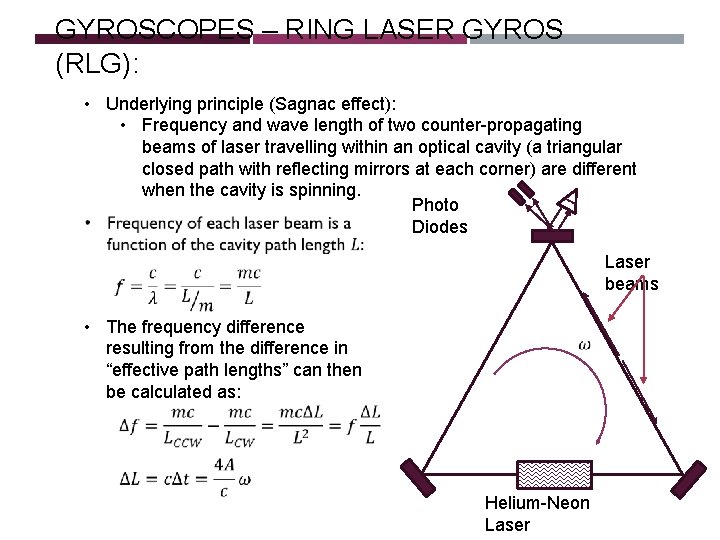
GYROSCOPES – RING LASER GYROS (RLG): • Underlying principle (Sagnac effect): • Frequency and wave length of two counter-propagating beams of laser travelling within an optical cavity (a triangular closed path with reflecting mirrors at each corner) are different when the cavity is spinning. Photo Diodes Laser beams • The frequency difference resulting from the difference in “effective path lengths” can then be calculated as: Helium-Neon Laser

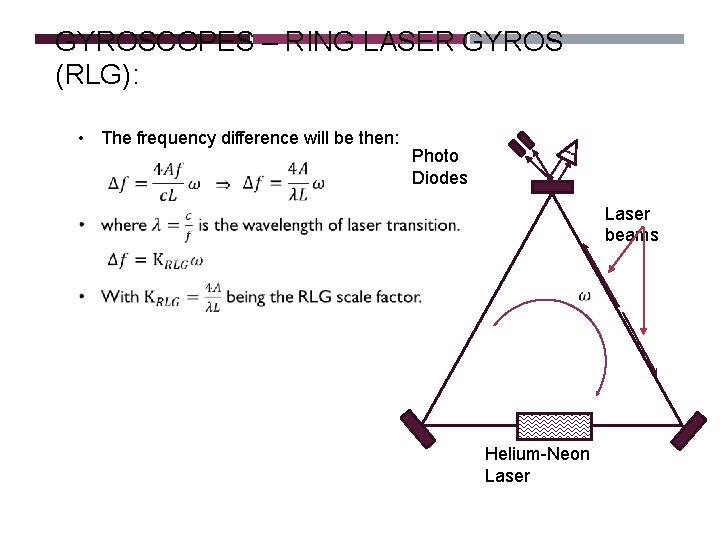
GYROSCOPES – RING LASER GYROS (RLG): • The frequency difference will be then: Photo Diodes Laser beams Helium-Neon Laser

GYROSCOPES – RING LASER GYROS (RLG): • Lock-in effect: due to imperfections in the lasing cavity (mirrors), below an input rate thresholds, there would be no output frequency difference. • The lock-in dead zone is in the order of 100 deg/hr (earth rotation rate is 15 deg/hr) Dead zone • Mechanical dither the laser block at 400500 Hz, with peak amplitude of approximately 1 arc-sec to remove the dead zone.

GYROSCOPES – MEMS GYROS: • In 2 D, polar position coordinate of the object is: • Double differentiating with respect to time, gives the acceleration:

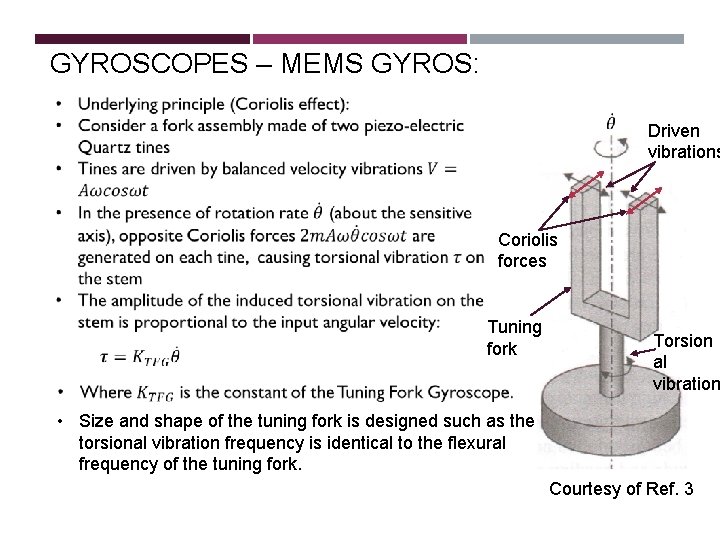
GYROSCOPES – MEMS GYROS: Driven vibrations Coriolis forces Tuning fork Torsion al vibration • Size and shape of the tuning fork is designed such as the torsional vibration frequency is identical to the flexural frequency of the tuning fork. Courtesy of Ref. 3

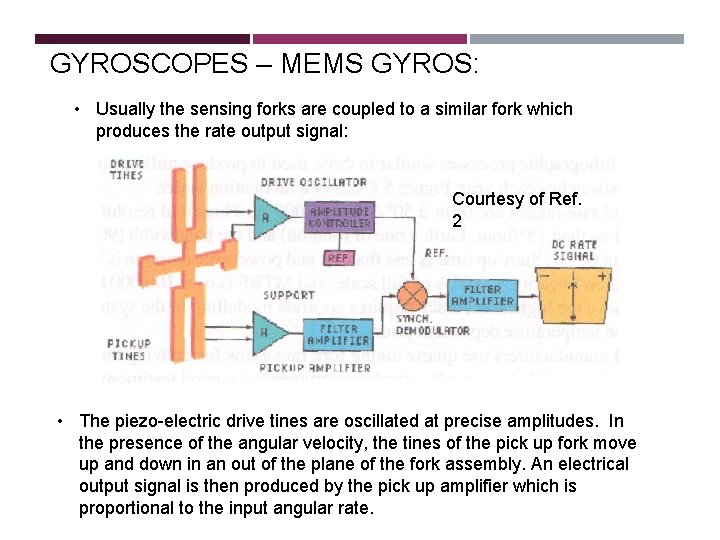
GYROSCOPES – MEMS GYROS: • Usually the sensing forks are coupled to a similar fork which produces the rate output signal: Courtesy of Ref. 2 Coriolis forces • The piezo-electric drive tines are oscillated at precise amplitudes. In the presence of the angular velocity, the tines of the pick up fork move up and down in an out of the plane of the fork assembly. An electrical output signal is then produced by the pick up amplifier which is proportional to the input angular rate.

GYROSCOPES – ERROR TERMS

GYROSCOPES – ERROR TERMS • Hence, the accumulated angle random walk error has a mean and covariance of [4]: • Hence the output angle random walk has zero mean and a variance which grows proportional to square root of time:

GYROSCOPES – ERROR TERMS Ref. 4

GYROSCOPES – ERROR TERMS • Flicker noise / Bias stability [4] • Bias of the MEMS gyro changes due to flicker noise (low frequency noise with a 1/f spectrum) • Bias fluctuations due to flicker noise is modelled as random walk (not accurate as the bias variance doesn’t grow with time).

GYROSCOPES – ERROR TERMS • Flicker noise / Bias stability [4] • The attitude error due to the bias fluctuations (with bias random walk model), would then be a second order angle random walk model. • Temperature variations: • Changes in the sensor bias due to the temperature changes (could be also caused due to the electronics self heating) • The effect is nonlinear usually of order 3 • Either the sensors must be calibrated with temperature or the sensors unit must be temperature controlled.

GYROSCOPES – ERROR TERMS – ALLAN VARIANCE

GYROSCOPES – ERROR TERMS – ALLAN VARIANCE • Allan variance method is plotted as a function of the averaging period T on a log-log scale • Different random process usually appear in different region of T: Courtesy of Ref. 5 T

GYROSCOPES – CALIBRATION • Calibration of the sensor suite is accomplished on temperature- controlled precise turn-tables (1 arcsec tilt accuracy) to determine the sensors bias, scale factor, misalignment factors, g-sensitivity factors, etc: • For gyroscopes: • For accelerometer: • Kalman Filter or Least Square method to determine the unknown calibration parameters.

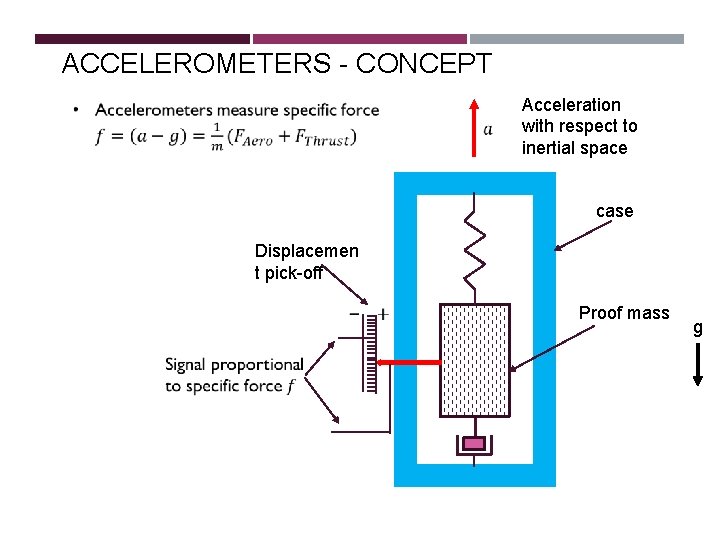
ACCELEROMETERS - CONCEPT Acceleration with respect to inertial space case Displacemen t pick-off Proof mass g

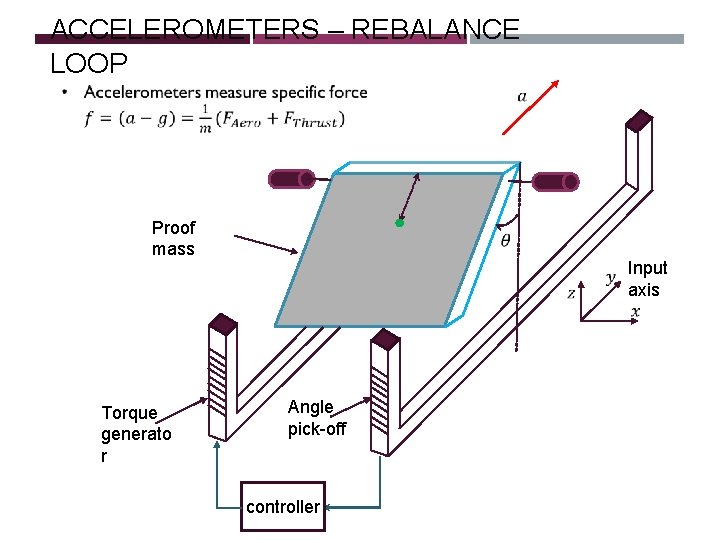
ACCELEROMETERS – REBALANCE LOOP Proof mass Torque generato r Angle pick-off controller Input axis

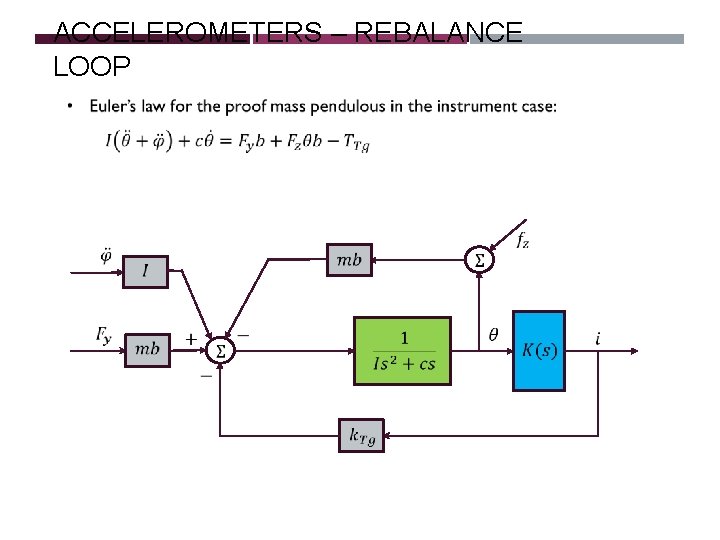
ACCELEROMETERS – REBALANCE LOOP

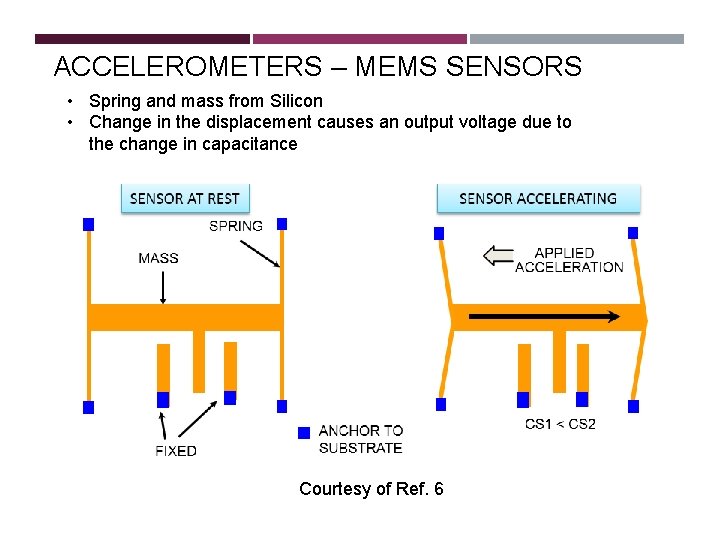
ACCELEROMETERS – MEMS SENSORS • Spring and mass from Silicon • Change in the displacement causes an output voltage due to the change in capacitance Courtesy of Ref. 6

REFERENCES 1. A. Lawrence, Modern Inertial Technology, Springer, 1998 2. R. P. G. Collinson, Introduction to Avionic Systems, third edition, Springer. 3. D. H. Titterton and J. L. Weston, Strapdown Inertial Navigation Technology, Peter Peregrinus, Ltd. , 1997. 4. O. J. Woodman, An Introduction to inertial navigation. Technical Report, University of Cambridge, 2007. 5. IEEE Std 962 -1997 (R 2003) Standard Specification Format Guide and Test Procedure fro Single-Axis Interferometric Fiber Optic Gyros, Annex C. IEEE, 2003. 6. www. ett. bme. hu/memsedu