Straight Line Graphs Objective Understand that all straight

Straight Line Graphs

Objective Understand that all straight line graphs can be represented in the form y=mx+c, and be able to state the equation of given graphs. State the gradient and y intercept given the equation

All straight lines can be written in the form y = mx + c You need to be able to write down the equation of a straight line by working out the values for m and c. It’s not as hard as you might think!

c is the constant value – this part of the equation does not change. y = mx + c m is the gradient of the line Why use m? This type of equation was made popular by the French Mathematician Rene Descartes. “m” could stand for “Monter” – the French word meaning “to climb”.

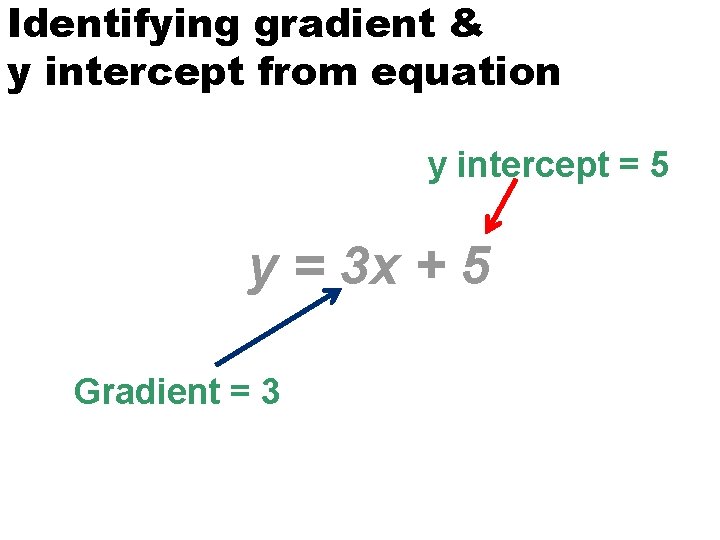
Identifying gradient & y intercept from equation y intercept = 5 y = 3 x + 5 Gradient = 3

Identifying gradient & y intercept from equation • y = 2 x + 2 • m=2, c=2 • y = 5 x – 9 • m = 5 , c = -9 • y = -2 x + 1 • m = -2 , c = 1 • y = 1/2 x -3 • m = 1/2 , c = -3 • y = -x + 10 • m = -1 , c = 10 • 2 y = 4 x + 3 • m = 2, c = 1. 5

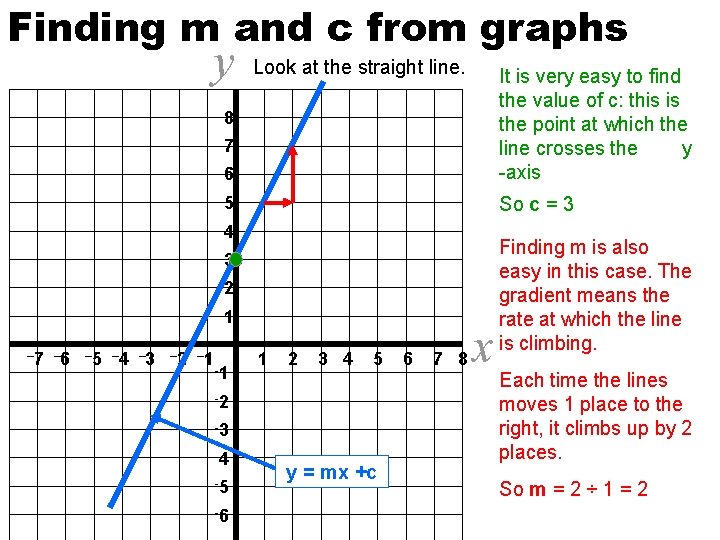
Finding m and c from graphs y Look at the straight line. 6 It is very easy to find the value of c: this is the point at which the line crosses the y -axis 5 So c = 3 8 7 4 3 2 1 – 7 – 6 – 5 – 4 – 3 – 2 – 1 -1 1 2 3 4 5 -2 -3 -4 -5 -6 yy == mx 2 x +3 +c 6 7 8 x Finding m is also easy in this case. The gradient means the rate at which the line is climbing. Each time the lines moves 1 place to the right, it climbs up by 2 places. So m = 2 ÷ 1 = 2

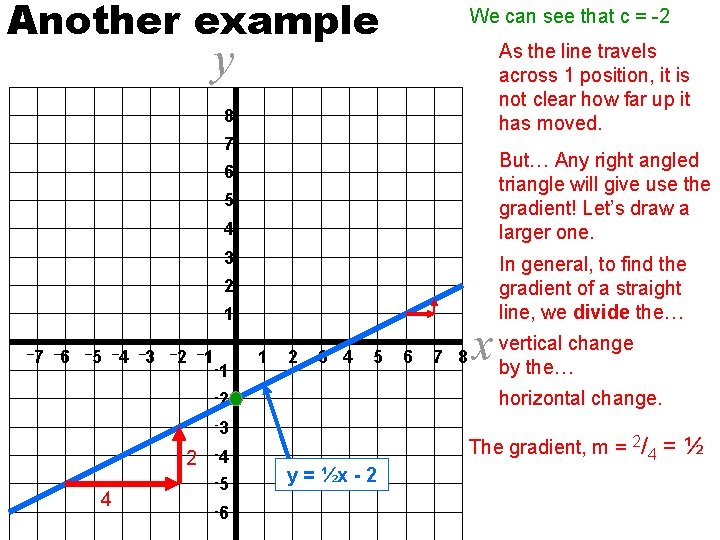
Another example We can see that c = -2 y As the line travels across 1 position, it is not clear how far up it has moved. 8 7 But… Any right angled triangle will give use the gradient! Let’s draw a larger one. 6 5 4 3 In general, to find the gradient of a straight line, we divide the… 2 1 – 7 – 6 – 5 – 4 – 3 – 2 – 1 -1 1 2 3 4 5 -3 2 4 -5 -6 7 8 change x vertical by the… horizontal change. -2 -4 6 y = mx ½x -+c 2 The gradient, m = 2/4 =½

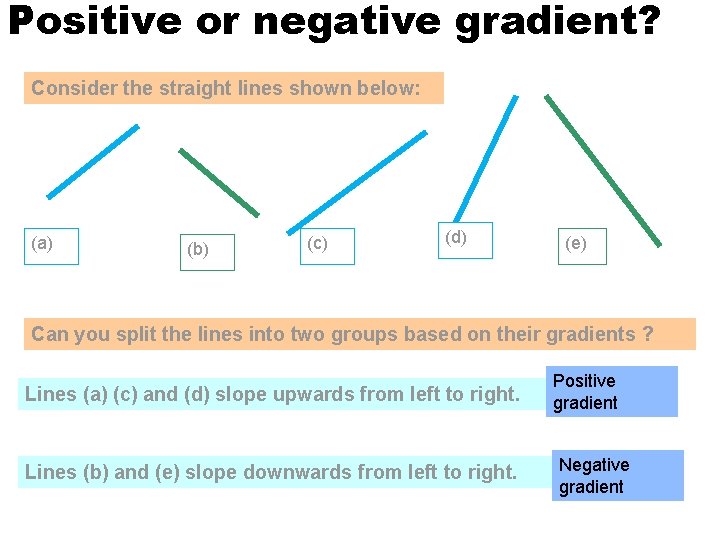
Positive or negative gradient? Consider the straight lines shown below: (a) (b) (c) (d) (e) Can you split the lines into two groups based on their gradients ? Lines (a) (c) and (d) slope upwards from left to right. Lines (b) and (e) slope downwards from left to right. Positive gradient Negative gradient

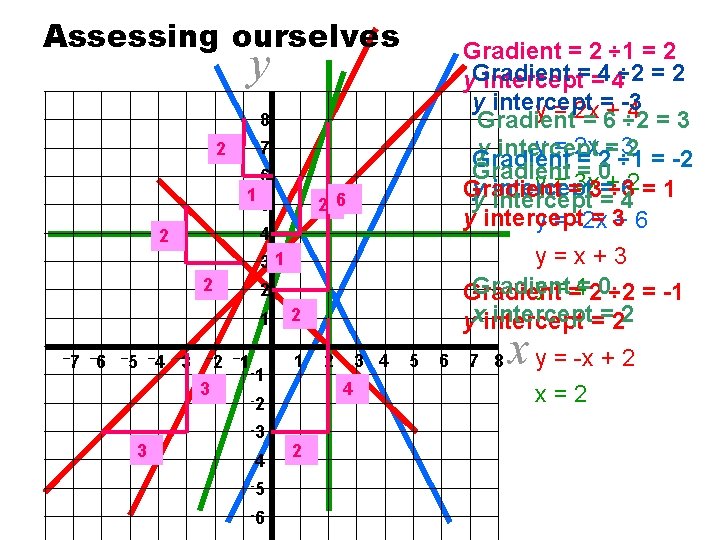
Assessing ourselves y Gradient = 2 ÷ 1 = 2 y. Gradient intercept==44÷ 2 = 2 y intercept =+-3 y = 2 x 4 =3 Gradient = 6 ÷ 2 y = 2 x = - 32 y intercept Gradient = 2 ÷ 1 = -2 Gradient = 0 y ==3 x 3=+÷ 3 2= 1 y intercept 6 Gradient y intercept = 4 y intercept = 3+ 6 y = -2 x y=x+3 Gradient y ==4=20÷ 2 = -1 Gradient intercept==22 yxintercept 8 7 2 1 6 2 6 5 4 2 31 2 2 1 – 7 – 6 – 5 – 4 – 3 – 2 – 1 3 3 -1 2 1 -4 -5 -6 3 4 4 -2 -3 2 2 5 6 7 8 x y = -x + 2 x=2

Did you meet the objective? You should : • Be able to state the equation of graphs in the form of y = mx + c • Be able to state the gradient & y intercept from any given equation