Stock Flow Diagrams James R Burns 1 What

Stock & Flow Diagrams James R. Burns 1

What are stocks and flows? ? n n A way to characterize systems as stocks and flows between stocks Stocks are variables that accumulate the affects of other variables Rates are variables the control the flows of material into and out of stocks Auxiliaries are variables that modify information as it is passed from stocks to rates 2

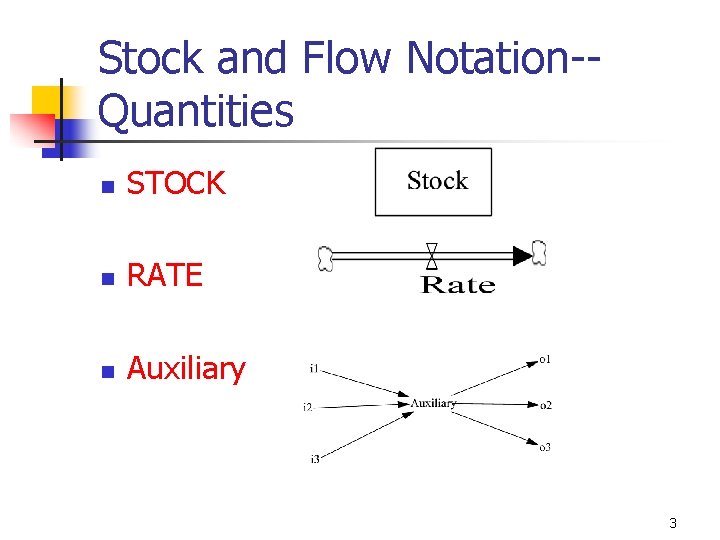
Stock and Flow Notation-Quantities n STOCK n RATE n Auxiliary 3

Stock and Flow Notation-Quantities n Input/Parameter/Lookup n n Have no edges directed toward them Output n Have no edges directed away from them 4

Inputs and Outputs n n n Inputs Parameters Lookups n n Inputs are controllable quantities Parameters are environmentally defined quantities over which the identified manager cannot exercise any control Lookups are TABLES used to modify information as it is passed along Outputs n Have no edges directed away from them 5

Stock and Flow Notation-edges n Information n Flow 6

Review of the Methodology n n n n Acquire verbal descriptions List variables, constants, parameters Delineate Causal Loop Diagram Translate CLD to Stock-and-Flow Diagram Delineate SFT in VENSIM Determine equations Run simulations, conducting “what if” experiments 7

Some rules n There are two types of causal links in causal models n n Information Flow Information proceeds from stocks and parameters/inputs toward rates where it is used to control flows Flow edges proceed from rates to states (stocks) in the causal diagram always 8

Robust Loops n n n In any loop involving a pair of quantities/edges, one quantity must be a rate the other a state or stock, one edge must be a flow edge the other an information edge 9

CONSISTENCY n n All of the edges directed toward a quantity are of the same type All of the edges directed away from a quantity are of the same type 10

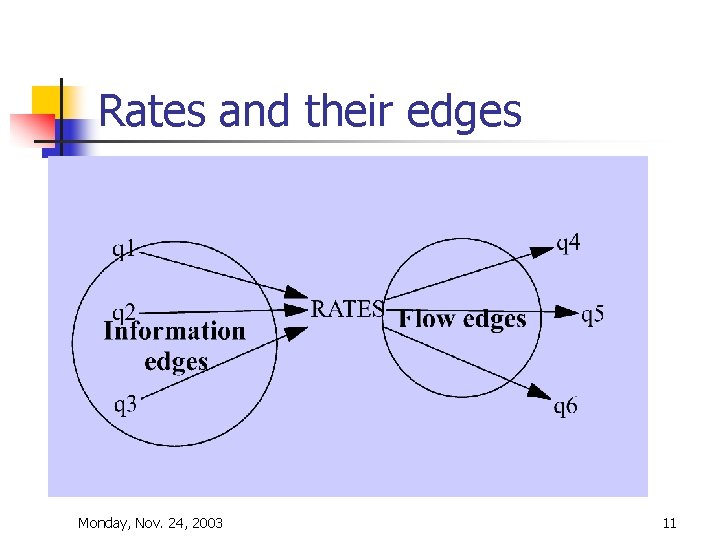
Rates and their edges Monday, Nov. 24, 2003 11

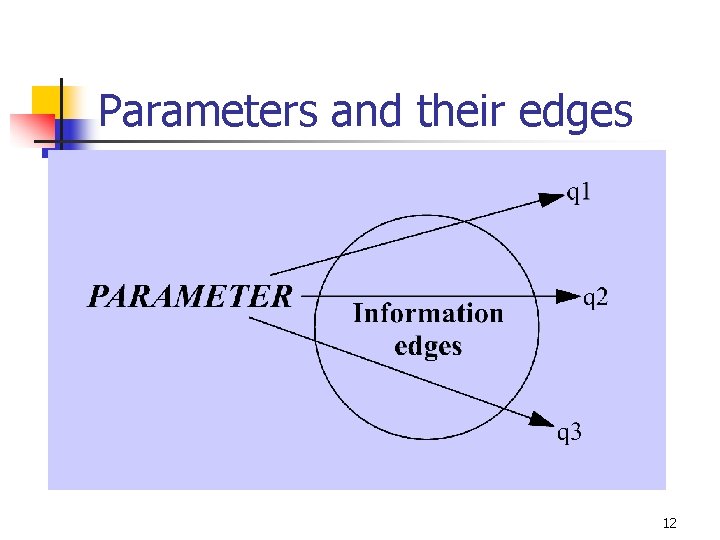
Parameters and their edges 12

Stocks and their edges 13

Auxiliaries and their edges 14

Outputs and their edges Monday, Nov. 24, 2003 15

STEP 1: Identify parameters n Parameters have no edges directed toward them 16

STEP 2: Identify the edges directed from parameters n These are information edges always 17

STEP 3: By consistency identify as many other edge types as you can 18

STEP 4: Look for loops involving a pair of quantities only n Use the rules for robust loops identified above Monday, Nov. 24, 2003 19

Monday, Nov. 24, 2003 20

Monday, Nov. 24, 2003 21

Monday, Nov. 24, 2003 22

Distinguishing Stocks & Flows by Name NAME UNITS Stock or flow n Revenue n Liabilities n Employees n Depreciation n Construction starts n Hiring n material standard of living Monday, Nov. 24, 2003 23

System Dynamics Software n STELLA and I think n n n Vensim n n n High Performance Systems, Inc. best fit for K-12 education Ventana systems, Inc. Free from downloading off their web site: www. vensim. com Robust--including parametric data fitting and optimization best fit for higher education Powersim What Arthur Andersen is using Monday, Nov. 24, 2003 n 24

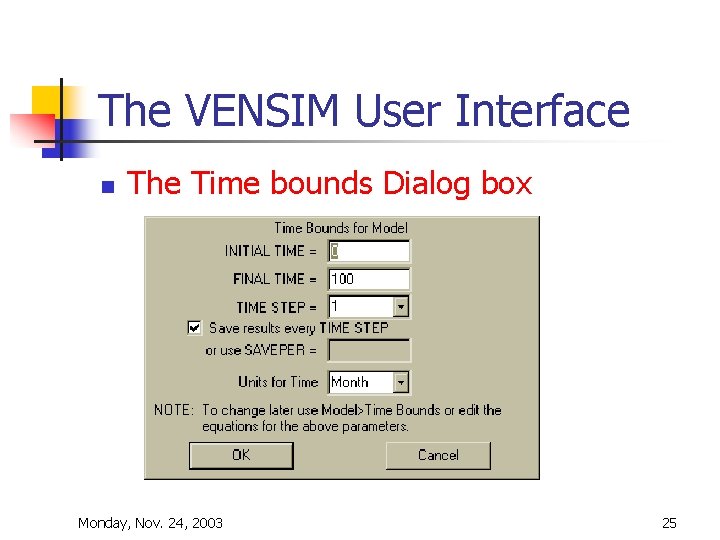
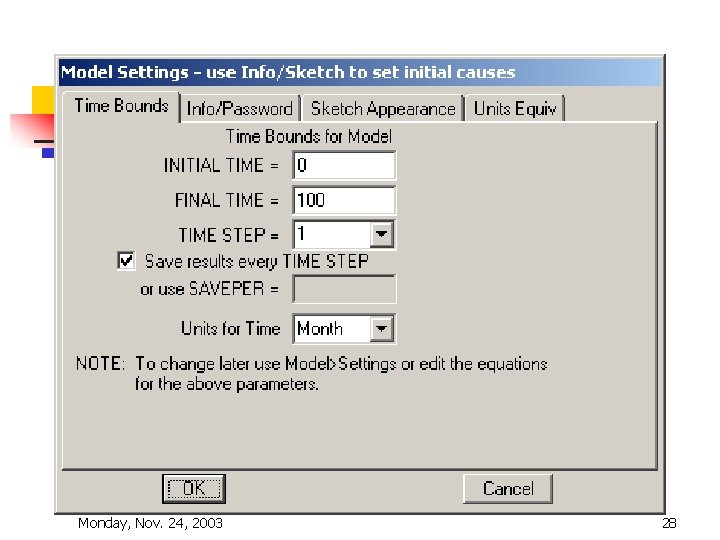
The VENSIM User Interface n The Time bounds Dialog box Monday, Nov. 24, 2003 25

Monday, Nov. 24, 2003 26

Monday, Nov. 24, 2003 27

Monday, Nov. 24, 2003 28

A single-sector Exponential growth Model n n n Consider a simple population with infinite resources--food, water, air, etc. Given, mortality information in terms of birth and death rates, what is this population likely to grow to by a certain time? Over a period of 200 years, the population is impacted by both births and deaths. These are, in turn functions of birth rate norm and death rate norm as well as population. A population of 1. 6 billion with a birth rate norm of. 04 and a death rate norm of. 028 Monday, Nov. 24, 2003 29

Let’s Begin by Listing Quantities n n n Population Births Deaths Birth rate norm Death rate norm Monday, Nov. 24, 2003 30

Monday, Nov. 24, 2003 31

Monday, Nov. 24, 2003 32

Equations n n n Birth rate = Birth rate norm * Population Death rate = Death rate norm * Population(t + dt) = Population(t) + dt*(Birth rate – Death rate) t = t + dt Population must have an initial defining value, like 1. 65 E 9 Monday, Nov. 24, 2003 33

Units Dissection n Birth rate = Birth rate Norm * Population [capita/yr] = [capita/capita*yr] * [capita] Monday, Nov. 24, 2003 34

Monday, Nov. 24, 2003 35

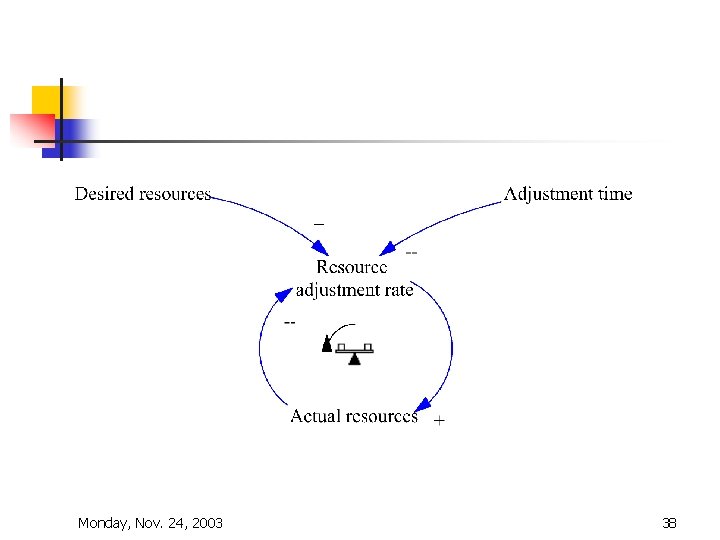
A single-sector Exponential goal-seeking Model Sonya Magnova is a resources planner for a school district. Sonya wishes to a maintain a desired level of resources for the district. Sonya’s new resource provision policy is quite simple--adjust actual resources AR toward desired resources DR so as to force these to conform as closely as possible. The time required to additional resources is AT. Actual resources are adjusted with a resource adjustment rate Monday, Nov. 24, 2003 n 36

What are the quantities? ? n n Actual resources Desired resources Resource adjustment rate Adjustment time Monday, Nov. 24, 2003 37

Monday, Nov. 24, 2003 38

Monday, Nov. 24, 2003 39

Equations n n n Adjustment time = constant Desired resources = variable or constant Resource adjustment rate = (Desired resources – Actual resources)/Adjustment time Actual resources(t + dt) = Actual resources(t) + dt*Resource adjustment rate Initial defining value for Actual resources Monday, Nov. 24, 2003 40

Equation dissection Resource adjustment rate = (Desired resources – Actual resources)/Adjustment time n An actual condition—Actual resources n A desired condition—Desired resources n A GAP—(Desired resources – Actual resources) n A way to express action based on the GAP: (Desired resources – Actual resources)/Adjustment time n Monday, Nov. 24, 2003 41

Units check Resource adjustment rate = (Desired resources – Actual resources)/Adjustment time [widgets/yr] = ([widgets] – [widgets])/[yr] CHECKS Notice that rates ALWAYS HAVE THE UNITS OF THE ASSOCIATED STOCK DIVIDED BY THE UNITS OF TIME, ALWAYS Monday, Nov. 24, 2003 42

(1) Actual Resources= INTEG (Resource adjustment rate, 10) Units: **undefined** (2)Adjustment time= 10 Units: **undefined** (3)Desired Resources= 1000 Units: **undefined** (4)FINAL TIME = 100 Units: Month The final time for the simulation. Monday, Nov. 24, 2003 43

(5)INITIAL TIME = 0 Units: Month The initial time for the simulation. (6)Resource adjustment rate= (Desired Resources - Actual Resources)/Adjustment time Units: **undefined** (7)SAVEPER = TIME STEP Units: Month [0, ? ] The frequency with which output is stored. (8)TIME STEP = 1 Units: Month [0, ? ] The time step for the simulation. Monday, Nov. 24, 2003 44

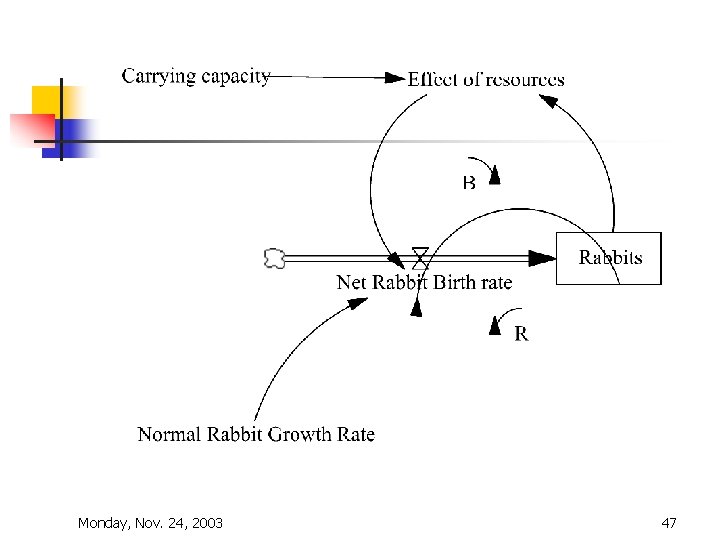
Shifting loop Dominance n n Rabbit populations grow rapidly with a reproduction fraction of. 125 per month When the population reaches the carrying capacity of 1000, the net growth rate falls back to zero, and the population stabilizes Starting with two rabbits, run for 100 months with a time step of 1 month (This model has two loops, an exponential growth loop (also called a reinforcing loop) and a balancing loop) Monday, Nov. 24, 2003 45

Shifting loop Dominance n n n Assumes the following relation for Effect of Resources = (carrying capacity Rabbits)/carrying capacity This is a multiplier Multipliers are always dimless (dimensionless) When rabbits are near zero, this is near 1 When rabbits are near carrying capacity, this is near zero n This will shut down the net rabbit birth rate Monday, Nov. 24, 2003 46

Monday, Nov. 24, 2003 47

Monday, Nov. 24, 2003 48

Dimensionality Considerations n n VENSIM will check for dimensional consistency if you enter dimensions Rigorously, all models must be dimensionally consistent What ever units you use for stocks, the associated rates must have those units divided by TIME An example follows Monday, Nov. 24, 2003 49

Cascaded rate-state (stock) combinations n In the oil exploration industry, unproven reserves (measured in barrels) become proven reserves when they are discovered. The extraction rate transforms proven reserves into inventories of crude. The refining rate transforms inventories of crude into refined petroleum products. The consumption rate transforms refined products into pollution (air, heat, etc. ) Monday, Nov. 24, 2003 50

Another cascaded rate-stock combination n Population cohorts. Suppose population is broken down into age cohorts of 015, 16 -30, 31 -45, 46 -60, 61 -75, 76 -90 Here each cohort has a “lifetime” of 15 years Again, each rate has the units of the associated stocks divided by time Monday, Nov. 24, 2003 51

Project Dynamics n Projects begin with a huge block of uncompleted work. Eventually, all of this work gets completed. The rate at which uncompleted work gets finished and thus enters the realm of completed work is called the work rate. Obviously, the work rate would be a function of the number of workers, the efficiency with which they work and so forth. Monday, Nov. 24, 2003 52

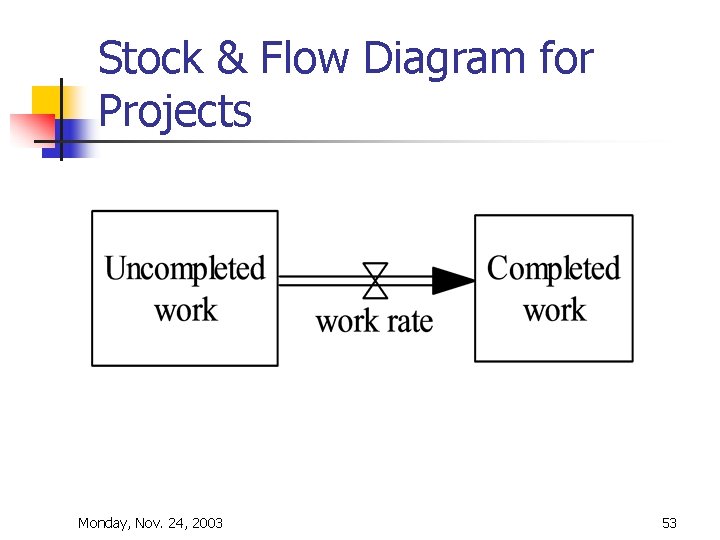
Stock & Flow Diagram for Projects Monday, Nov. 24, 2003 53

The Sector Approach to the Determination of Structure n n What is meant by “sector? ” What are the steps… n n to determination of structure within sectors? to determination of structure between sectors? Monday, Nov. 24, 2003 54

Definition of sector n n All the structure associated with a single flow Note that there could be several states associated with a single flow n The next sector in the pet population model has three states in it Monday, Nov. 24, 2003 55

Sector Methodology, Overall n n Identify flows (sectors) that must be included within the model Develop the structure within each sector of the model. n Use standard one-sector sub-models or develop the structure within the sector from scratch using the steps in Table 15. 5 Monday, Nov. 24, 2003 56

Sector Methodology, Overall Cont’d n n Develop the structure between all sectors that make up the model Implement the structure in a commercially available simulation package Monday, Nov. 24, 2003 57

Steps Required to Formulate the Structure for a Sector from Scratch n n n Specify the quantities required to delineate the structure within each sector Determine the interactions between the quantities and delineate the resultant causal diagram Classify the quantity and edge types and delineate the flow diagram Monday, Nov. 24, 2003 58

Resource, facility and infrastructure (desks, chairs, computers, networks, labs, etc. ) needs for an educational entity are driven by a growing population that it serves. Currently, the population stands at 210, 000 and is growing at the rate of two percent a year. One out of every three of these persons is a student. n One teacher is needed for every 25 students. Currently, there are 2, 300 actual teachers; three percent of these leave each year. Construct a structure for each that drives the actual level toward the desired level. Assume an adjustment time of one year. Set this up in VENSIM to run for 25 years, with a Monday, Nov. 24, 2003 59 time-step of. 25 years. n

One-hundred square feet of facility space is needed for each student. Thirty-five hundred dollars in infrastructure is needed for each student. Currently, there is five million sq. ft of facility space, but this becomes obsolescent after fifty years. Currently, there is $205, 320, 000 in infrastructure investment, but this is fully depreciated after ten years. For each of infrastructure, teachers and facility space, determine a desired level or stock for the same. Construct a structure for each that drives the actual level toward the Monday, Nov. 24, 2003 60 desired level. n

n Set this up in VENSIM to run for 25 years, with a time-step of. 25 years. Assume adjustment times of one year. DETERMINE HOW MUCH IN THE WAY OF FACILITIES, TEACHERS AND INFRASTRUCTURE ARE NEEDED PER YEAR OVER THIS TIME PERIOD. Monday, Nov. 24, 2003 61

What are the main sectors and how do these interact? n n Population Teacher resources Facilities Infrastructure Monday, Nov. 24, 2003 62

Factors affecting teacher departures n n n Inside vs. outside salaries Student-teacher ratios How might these affects be included? Monday, Nov. 24, 2003 63

Teacher departure description n It is known that when the ratio of average “inside the district” salary is comparable to outside salaries of positions that could be held by teachers, morale is normal and teacher departures are normal When the inside-side salary ratio is less than one, morale is low and departures are greater than normal The converse is true as well Monday, Nov. 24, 2003 64

Teacher departure description n n When student-teacher ratios exceed the ideal or desired student teacher ratio, which is twenty four, morale is low and again departures are greater than normal The converse is true as well Monday, Nov. 24, 2003 65

A Two-sector Housing/population Model n A resort community in Colorado has determined that population growth in the area depends on the availability of housing as well as the persistent natural attractiveness of the area. Abundant housing attracts people at a greater rate than under normal conditions. The opposite is true when housing is tight. Area Residents also leave the community at a certain rate due primarily to the availability of housing. Monday, Nov. 24, 2003 66

Two-sector Population/ housing Model, Continued n The housing construction industry, on the other hand, fluctuates depending on the land availability and housing desires. Abundant housing cuts back the construction of houses while the opposite is true when the housing situation is tight. Also, as land for residential development fills up (in this mountain valley), the construction rate decreases to the level of the demolition rate of houses. Monday, Nov. 24, 2003 67

What are the main sectors and how do these interact? n n Population Housing Monday, Nov. 24, 2003 68

What is the structure within each sector? n n Determine state/rate interactions first Determine necessary supporting infrastructure n n PARAMETERS AUXILIARIES Monday, Nov. 24, 2003 69

What does the structure within the population sector look like? n n n RATES: in-migration, out-migration, net death rate STATES: population PARAMETERS: in-migration normal, outmigration normal, net death-rate normal Monday, Nov. 24, 2003 70

What does the structure within the housing sector look like? n n n RATES: construction rate, demolition rate STATES: housing AUXILIARIES: Land availability multiplier, land fraction occupied PARAMETERS: normal housing construction, average lifetime of housing PARAMETERS: land occupied by each unit, total residential land Monday, Nov. 24, 2003 71

What is the structure between sectors? n There are only AUXILIARIES, PARAMETERS, INPUTS and OUTPUTS Monday, Nov. 24, 2003 72

What are the between-sector auxiliaries? n n n Housing desired Housing ratio Housing construction multiplier Attractiveness for in-migration multiplier PARAMETER: Housing units required person Monday, Nov. 24, 2003 73

Monday, Nov. 24, 2003 74