Stochastische Prozesse I Seminarvortrag von Elias Kellner 14











- Slides: 35

Stochastische Prozesse I Seminarvortrag von Elias Kellner 14. 06. 2007 1. 2. 3. 4. Zeitreihen Modellierung Analyse Beispiel: Kalmanfilter

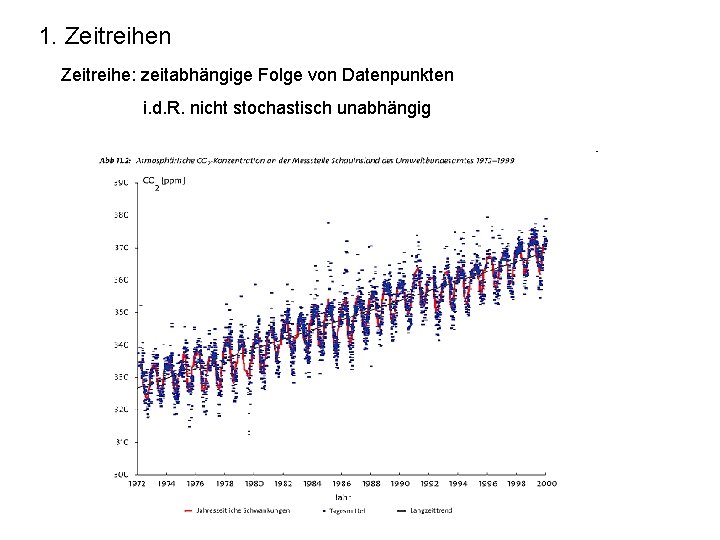
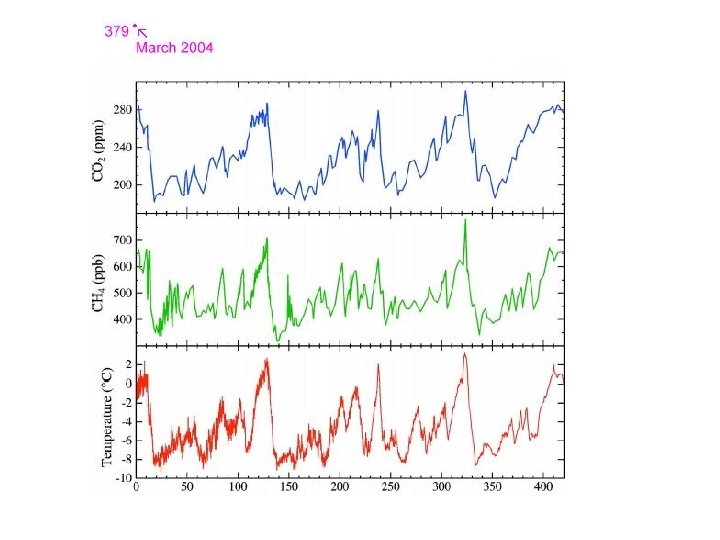
1. Zeitreihen Zeitreihe: zeitabhängige Folge von Datenpunkten i. d. R. nicht stochastisch unabhängig


Handschriftanalyse, Zeitreihe der vertikalen Geschwindigkeit

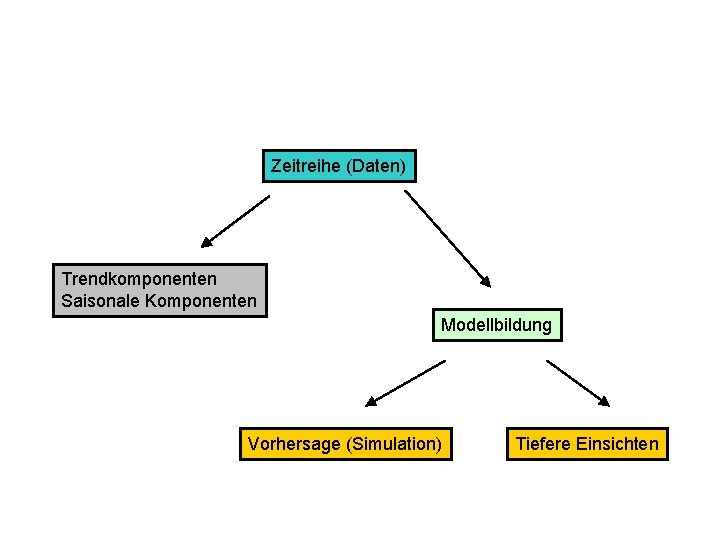
Zeitreihe (Daten) Trendkomponenten Saisonale Komponenten Modellbildung Vorhersage (Simulation) Tiefere Einsichten

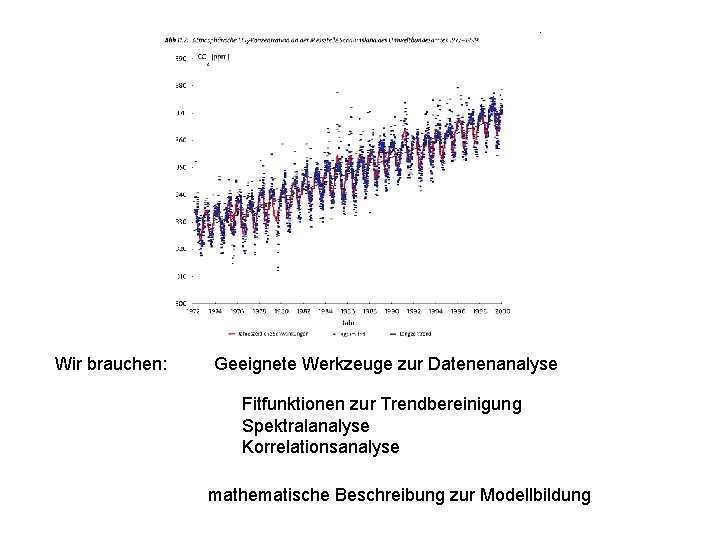
Wir brauchen: Geeignete Werkzeuge zur Datenenanalyse Fitfunktionen zur Trendbereinigung Spektralanalyse Korrelationsanalyse mathematische Beschreibung zur Modellbildung

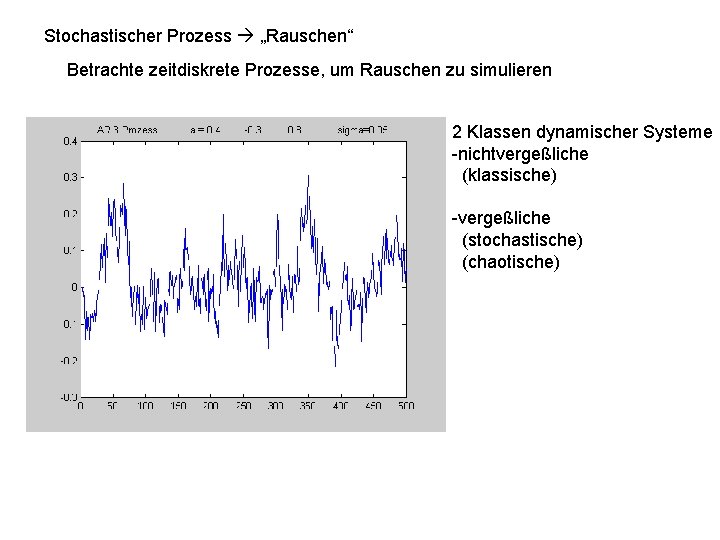
Stochastischer Prozess „Rauschen“ Betrachte zeitdiskrete Prozesse, um Rauschen zu simulieren 2 Klassen dynamischer Systeme -nichtvergeßliche (klassische) -vergeßliche (stochastische) (chaotische)

Prozess ( Verteilungen bekannt) Realisation Stationarität Eine Zeitreihe heißt stark stationär, wenn die Verteilung von nicht vom Index abhängt. Eine Zeitreihe heißt schwach stationär, wenn 1. 2. Autokovarianz

Ergodizität Ergodisch in klass. Mechanik: System kommt erlaubten Systemzuständen beliebig nahe Jeder Prozess induziert eine Dichte im Phasenraum. Mittelwerte müssen bezüglich dieser Dichte gebildet werden Für ergodische Systeme gilt: „Scharmittel = Zeitmittel“

Simulation des Rauschens: Summe von vielen stochastischen Einflüssen Zentraler GWS Rauschen gaußverteilt Weißes Rauschen (WN): Folge von unabhängigen Realisationen einer gaußverteilten Zufallsvariablen

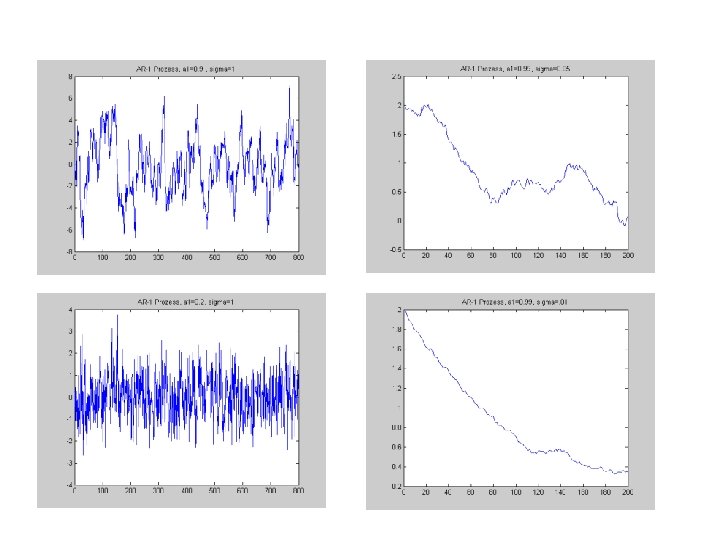
Modellierung durch AR-Prozesse Betrachte „vergesslichen“ Prozess Nehme an, xt sei linear durch die N vorherigen Datenpunkte bestimmt (Autoregession) Addiere zu jeden xt eine kleine Störung (Zufallsvariable, z. B. weisses Rauschen) AR(N) – Prozess:


Differenzengleichungen. Differenzengleichung = „diskretisierte“ Differentialgleichung Ansatz macht Sinn, da Natur i. a. durch Differentialgleichungen beschrieben wird. lineare DGL n‘ter Ordnung Rückführung von DGL n‘ter Ordnung auf System von DGL 1‘ter Ordnung z. B harmonischer Oszillator:

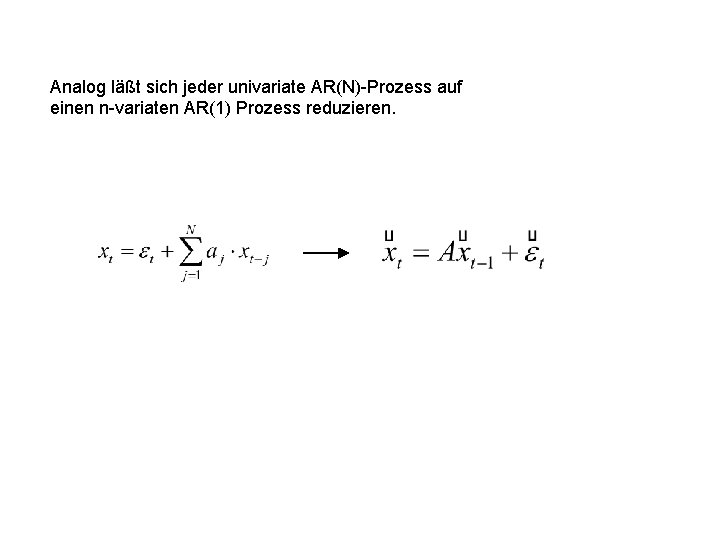
Analog läßt sich jeder univariate AR(N)-Prozess auf einen n-variaten AR(1) Prozess reduzieren.

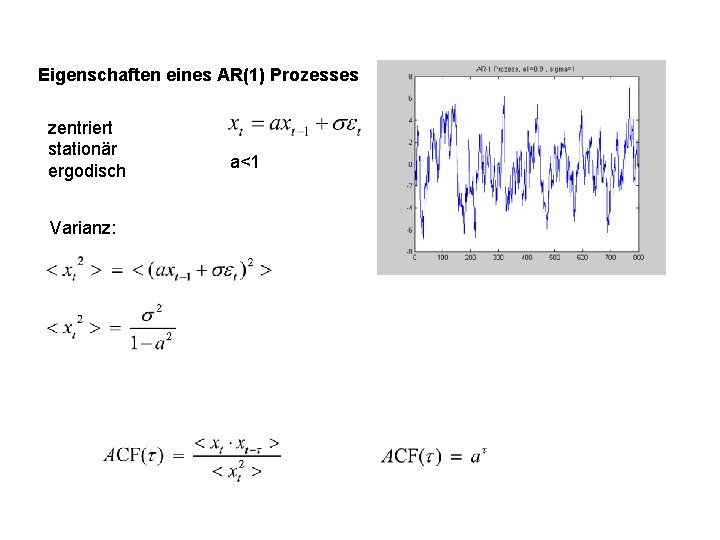
Eigenschaften eines AR(1) Prozesses zentriert stationär ergodisch Varianz: a<1

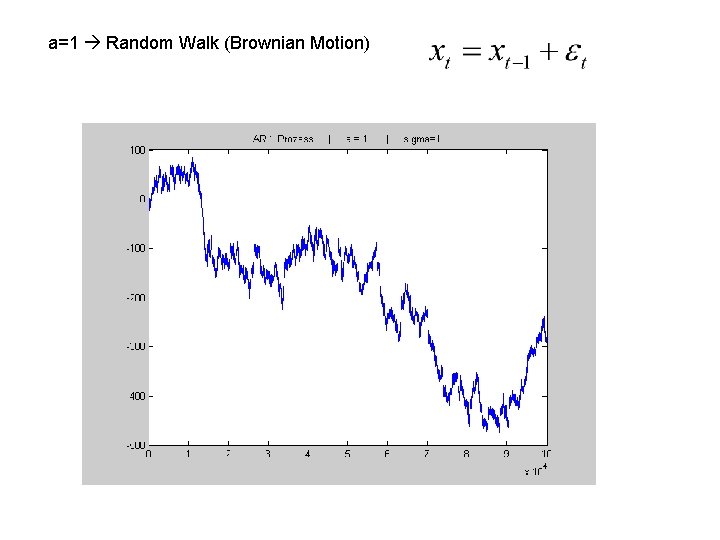
a=1 Random Walk (Brownian Motion)

AR(N) – Prozess: MA(N) – Prozess: (gleitendes Mittel) ARMA(p, q)

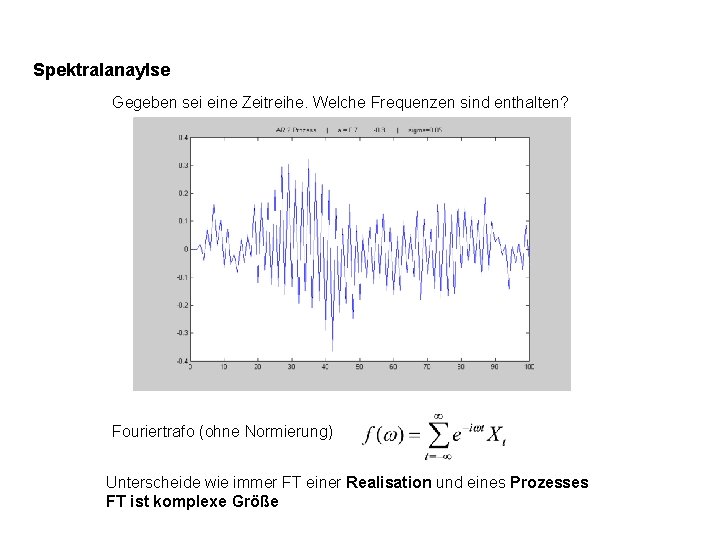
Spektralanaylse Gegeben sei eine Zeitreihe. Welche Frequenzen sind enthalten? Fouriertrafo (ohne Normierung) Unterscheide wie immer FT einer Realisation und eines Prozesses FT ist komplexe Größe

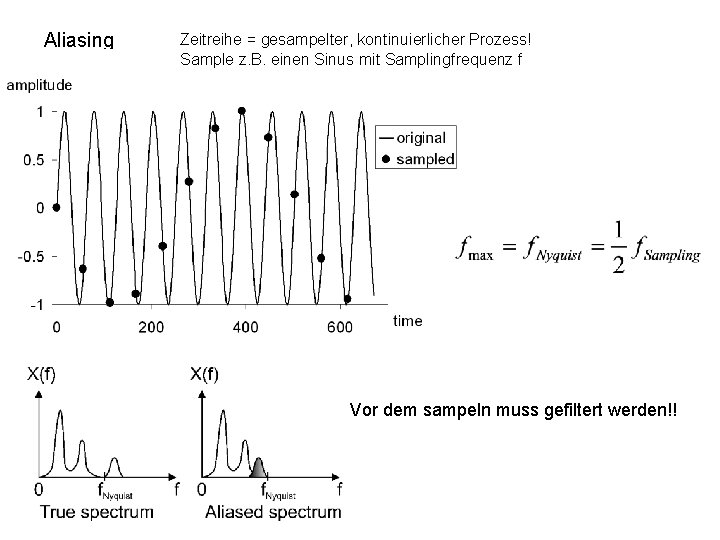
Aliasing Zeitreihe = gesampelter, kontinuierlicher Prozess! Sample z. B. einen Sinus mit Samplingfrequenz f Vor dem sampeln muss gefiltert werden!!

Spektrum Definiere Spektrum ACF einer Zeitreihe entspricht einer Faltung der Reihe mit sich selbst Faltung im Ortsraum enspricht Multiplikation im Frequenzraum. Multiplikation mit sich selbst ist | |2 Definition über ACF mathematisch korrekt, aber über FT leichter zu schätzen!

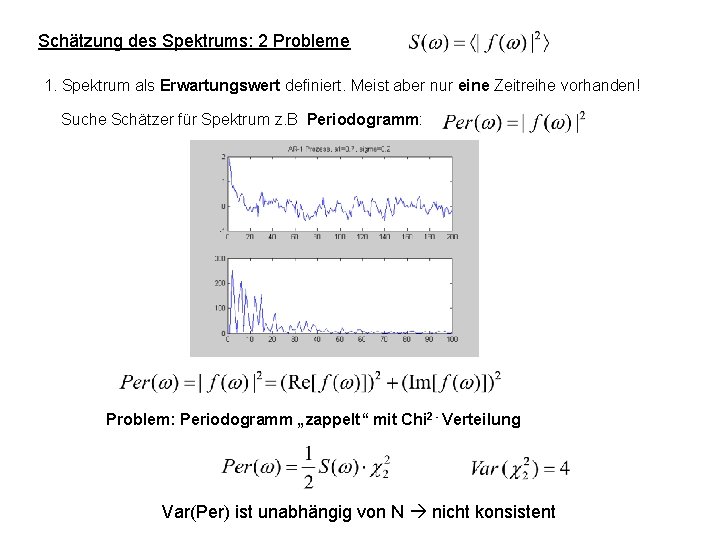
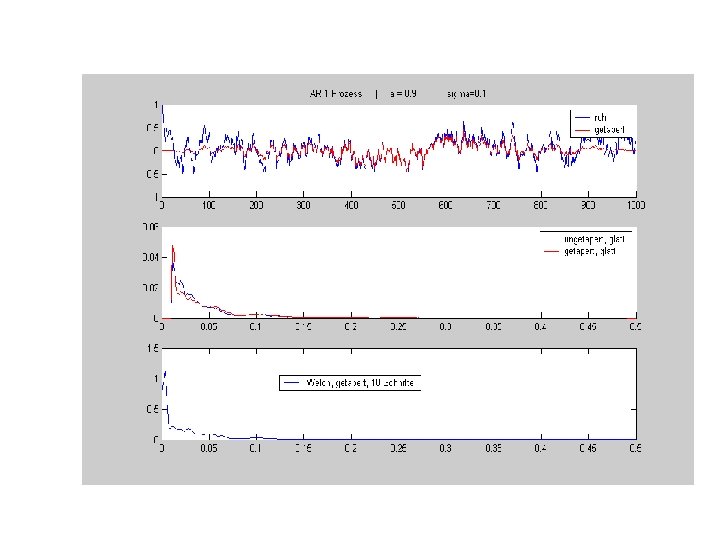
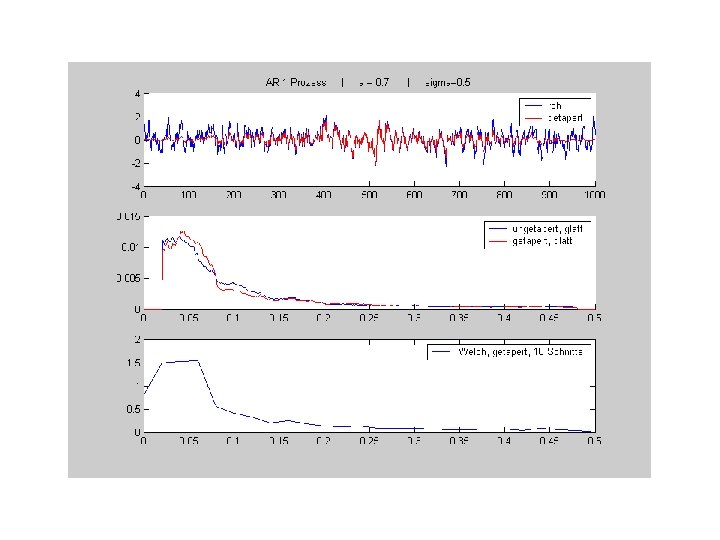
Schätzung des Spektrums: 2 Probleme 1. Spektrum als Erwartungswert definiert. Meist aber nur eine Zeitreihe vorhanden! Suche Schätzer für Spektrum z. B Periodogramm: Problem: Periodogramm „zappelt“ mit Chi 2 - Verteilung Var(Per) ist unabhängig von N nicht konsistent

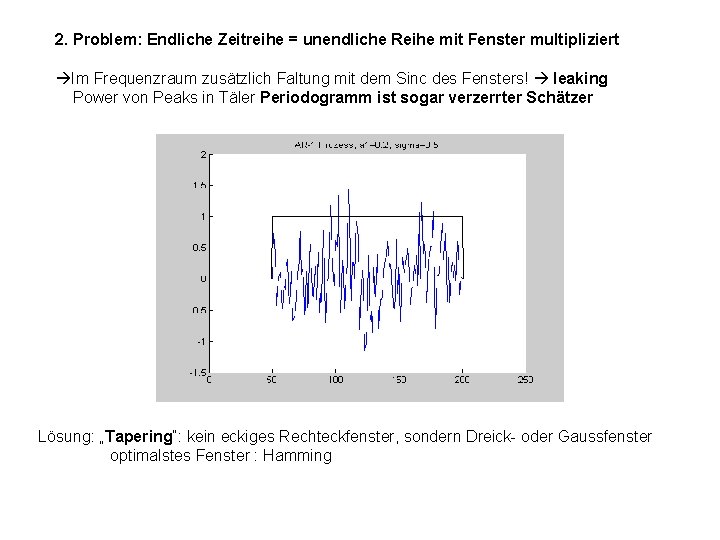
2. Problem: Endliche Zeitreihe = unendliche Reihe mit Fenster multipliziert Im Frequenzraum zusätzlich Faltung mit dem Sinc des Fensters! leaking Power von Peaks in Täler Periodogramm ist sogar verzerrter Schätzer Lösung: „Tapering“: kein eckiges Rechteckfenster, sondern Dreick- oder Gaussfenster optimalstes Fenster : Hamming

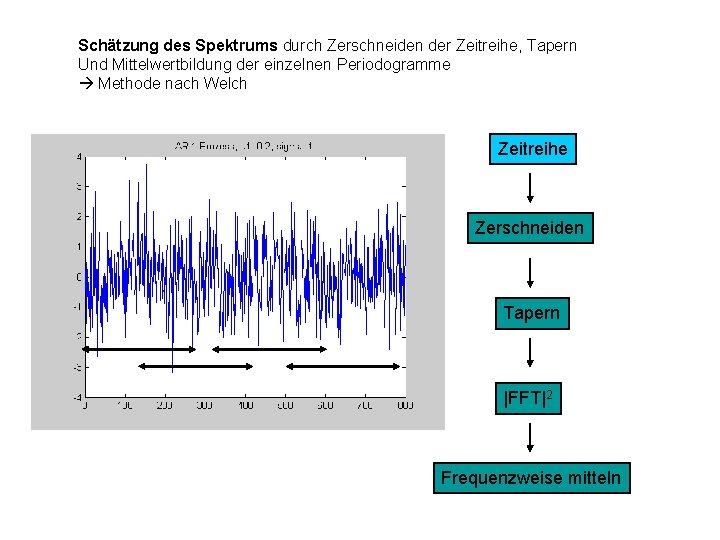
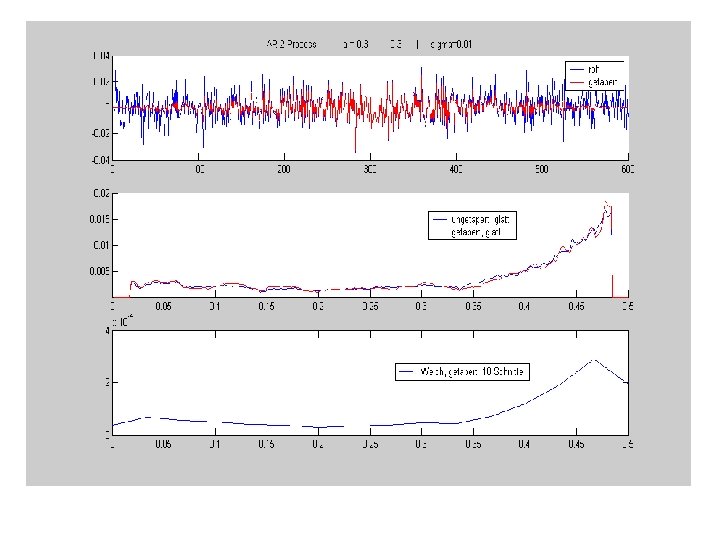
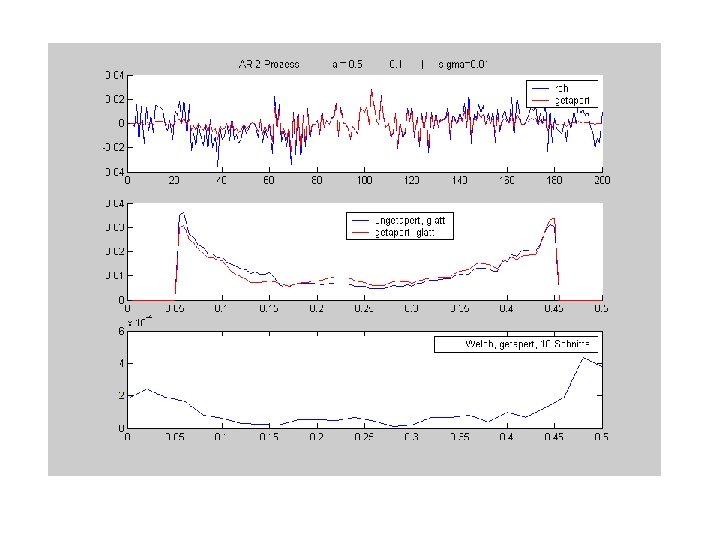
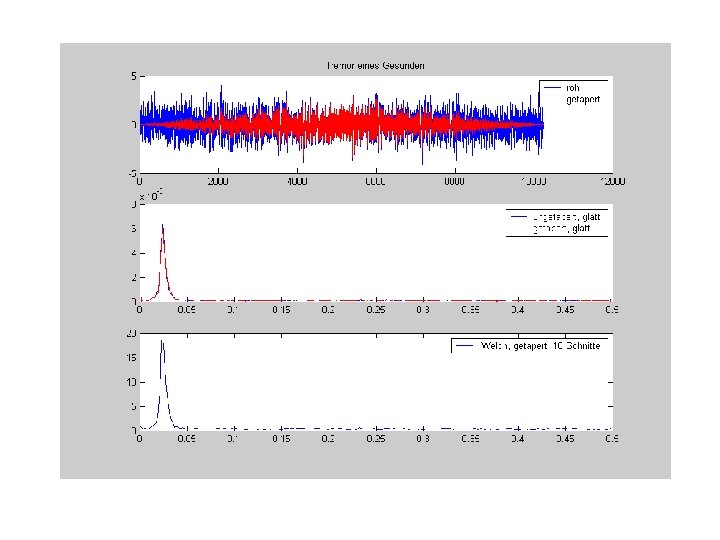
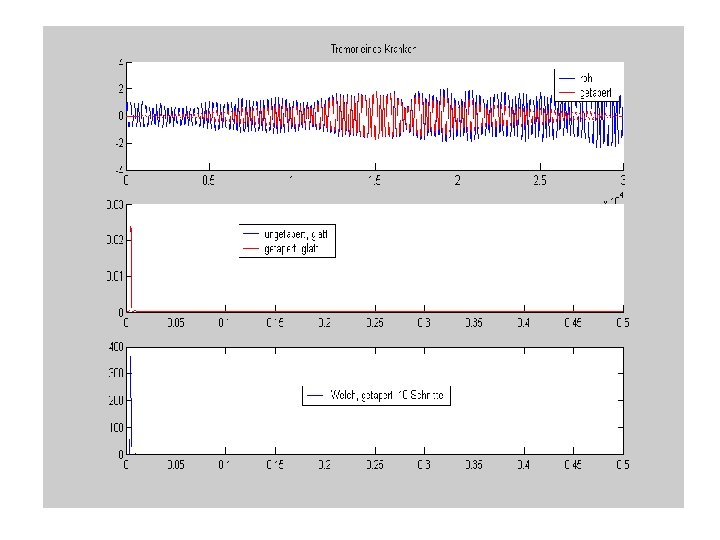
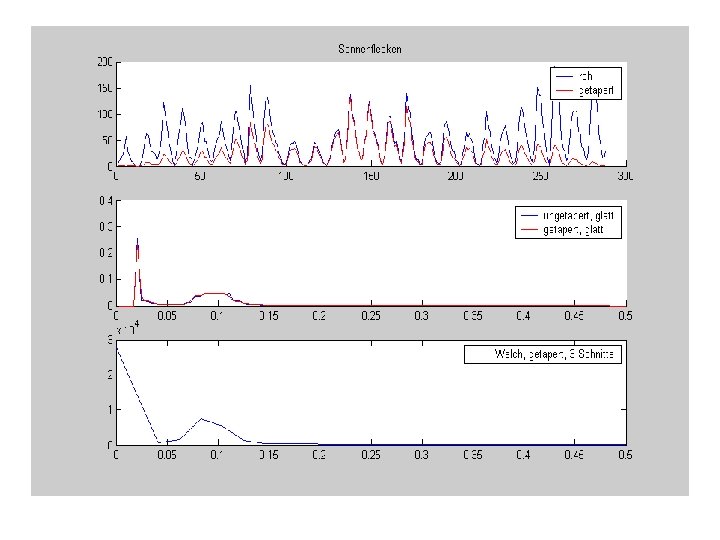
Schätzung des Spektrums durch Zerschneiden der Zeitreihe, Tapern Und Mittelwertbildung der einzelnen Periodogramme Methode nach Welch Zeitreihe Zerschneiden Tapern |FFT|2 Frequenzweise mitteln








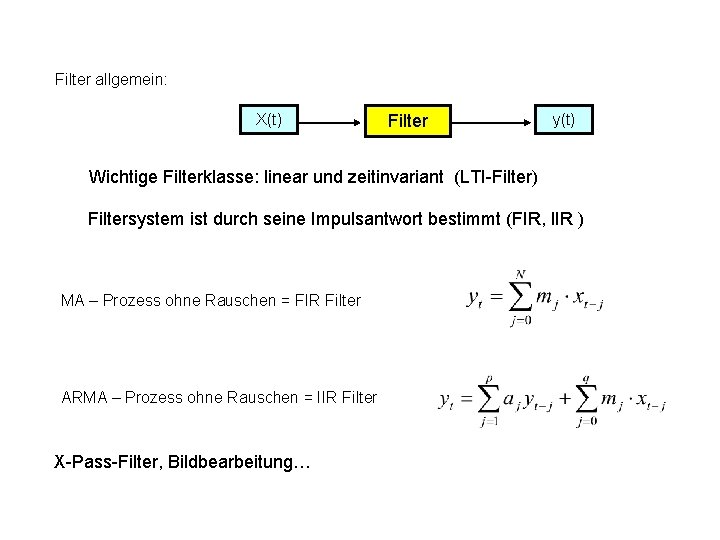
Filter allgemein: X(t) Filter y(t) Wichtige Filterklasse: linear und zeitinvariant (LTI-Filter) Filtersystem ist durch seine Impulsantwort bestimmt (FIR, IIR ) MA – Prozess ohne Rauschen = FIR Filter ARMA – Prozess ohne Rauschen = IIR Filter X-Pass-Filter, Bildbearbeitung…

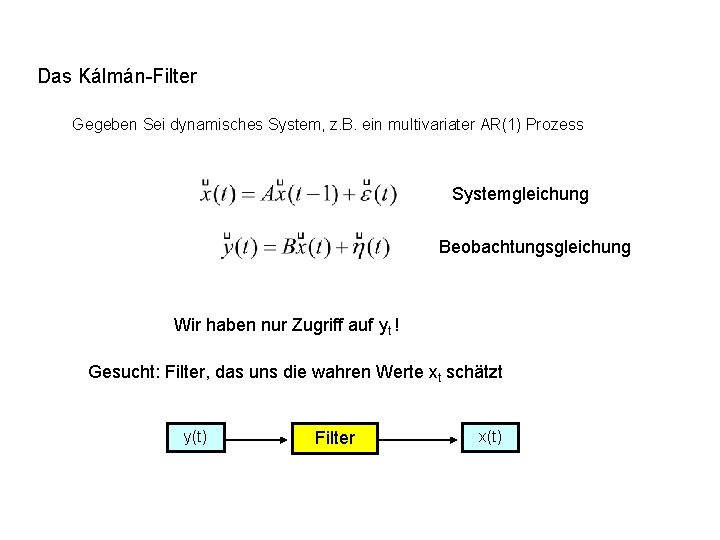
Das Kálmán-Filter Gegeben Sei dynamisches System, z. B. ein multivariater AR(1) Prozess Systemgleichung Beobachtungsgleichung Wir haben nur Zugriff auf yt ! Gesucht: Filter, das uns die wahren Werte xt schätzt y(t) Filter x(t)

Systemgleichung Beobachtungsgleichung Einfache Schätzung: Rückrechnen auf xt durch B-1 Große Fehler wegen Beobachtungsrauschen Man kann ausnutzen, dass man die Dynamik A des Systems kennt 1. Prädiktionsschritt: Beobachte y(t), berechne daraus Fehler y(t|t-1) - y(t) 2. Korrektur

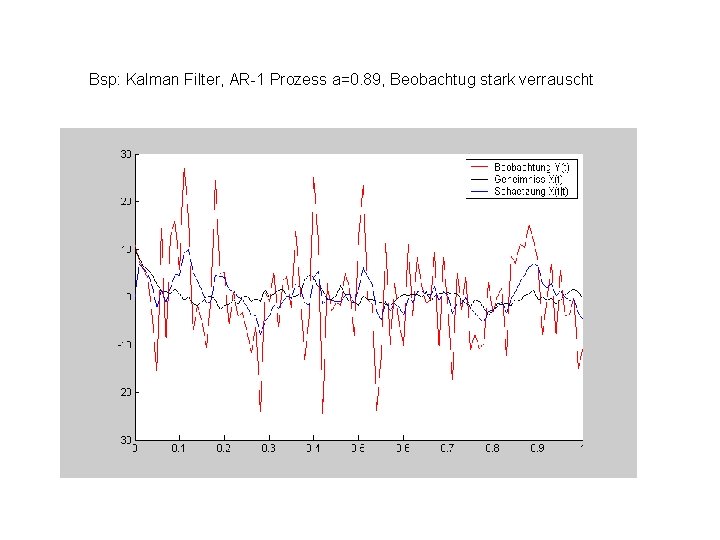
Bsp: Kalman Filter, AR-1 Prozess a=0. 89, Beobachtug stark verrauscht

Zusammenfassung AR-Prozesse Spektrum schätzen: Schneiden - Tapern – Periodogramme mitteln
 Ergodischer prozess
Ergodischer prozess Prozessarbeit dynamische prozesse
Prozessarbeit dynamische prozesse Morphologische prozesse
Morphologische prozesse Applet bernoulli wahrscheinlichkeit
Applet bernoulli wahrscheinlichkeit Stochastische unabhängigkeit
Stochastische unabhängigkeit Stochastische unabhängigkeit
Stochastische unabhängigkeit Stochastische unabhängigkeit würfelwurf
Stochastische unabhängigkeit würfelwurf Erasmus von rotterdam beeinflusst von
Erasmus von rotterdam beeinflusst von Raumschotkurs
Raumschotkurs Resposta
Resposta What is an alchemist
What is an alchemist Elias porter attitudes
Elias porter attitudes Norbert elias center
Norbert elias center Norbert elias sobre el tiempo
Norbert elias sobre el tiempo Profeta amos
Profeta amos Ruth elias
Ruth elias Ecg hanna
Ecg hanna Nikki seligman
Nikki seligman La pianta del cacao scuola primaria
La pianta del cacao scuola primaria Walt disney childhood
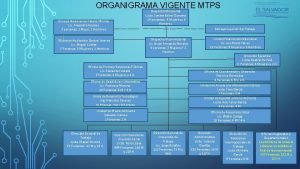
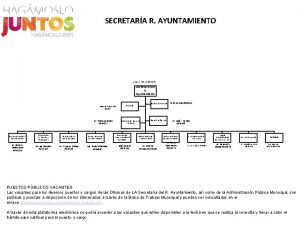
Walt disney childhood Organigrama de un despacho
Organigrama de un despacho Obediencia quiero y no sacrificio reina valera
Obediencia quiero y no sacrificio reina valera When was walt disney born
When was walt disney born Nombre elías que significa
Nombre elías que significa Quien era giezi el siervo de eliseo
Quien era giezi el siervo de eliseo Elias koutsoupias
Elias koutsoupias Semejanzas entre elías y juan el bautista
Semejanzas entre elías y juan el bautista Elias mallis
Elias mallis Caiu fogo do ceu e queimou o holocausto
Caiu fogo do ceu e queimou o holocausto Elias kunze
Elias kunze Elias baingana
Elias baingana Elias chaibub neto
Elias chaibub neto Elias daisy chain
Elias daisy chain Elias van gool
Elias van gool Eliseo cabrales
Eliseo cabrales Los tres elias
Los tres elias