Stochastic Systems Group A Motivating Application Sensor Array

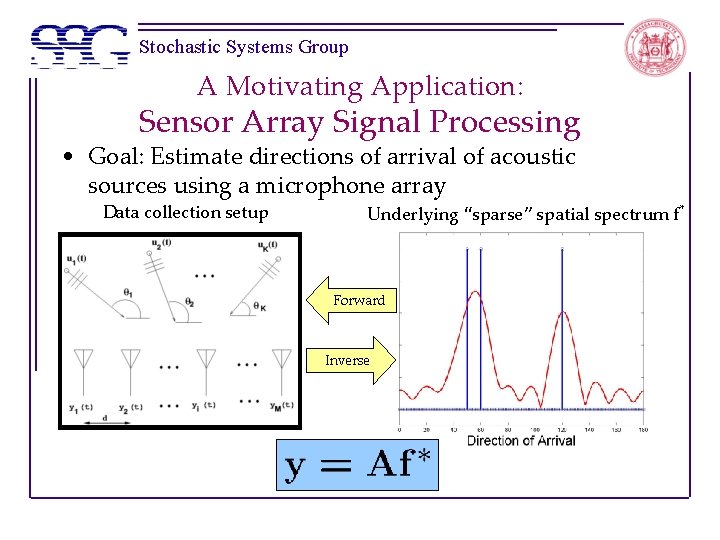
Stochastic Systems Group A Motivating Application: Sensor Array Signal Processing • Goal: Estimate directions of arrival of acoustic sources using a microphone array Data collection setup Underlying “sparse” spatial spectrum f* Forward Inverse

Stochastic Systems Group Underdetermined Linear Inverse Problems • Basic problem: find an estimate of , where [ • Underdetermined -- non-uniqueness of solutions • Additional information/constraints needed for a unique solution • A typical approach is the min-norm solution: • What if we know elements)? is sparse (i. e. has few non-zero ]

Stochastic Systems Group Sparsity constraints • Prefer the sparsest solution: Number of non-zero elements in f • Can be viewed as finding a sparse representation of the signal y in an overcomplete dictionary A • Intractable combinatorial optimization problem • Are there tractable alternatives that might produce the same result? • Empirical observation: l 1 -norm-based techniques produce solutions that look sparse – l 1 cost function can be optimized by linear programming!

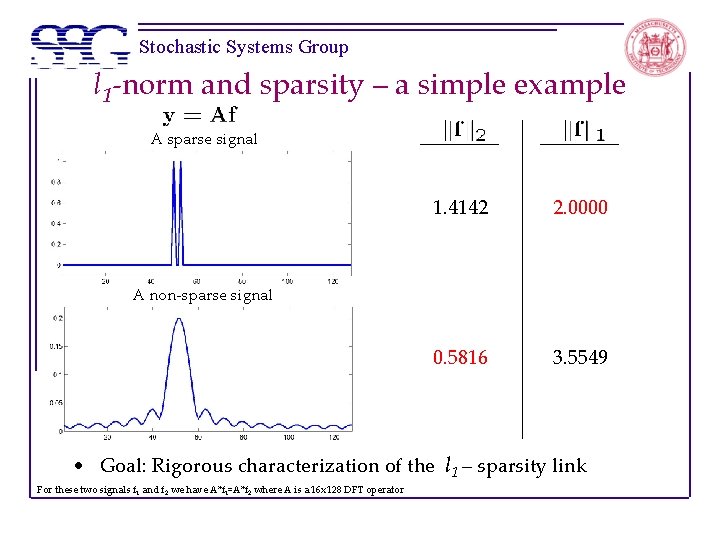
Stochastic Systems Group l 1 -norm and sparsity – a simple example A sparse signal 1. 4142 2. 0000 0. 5816 3. 5549 A non-sparse signal • Goal: Rigorous characterization of the l 1 – sparsity link For these two signals f 1 and f 2 we have A*f 1=A*f 2 where A is a 16 x 128 DFT operator

Stochastic Systems Group l 0 uniqueness conditions • Prefer the sparsest solution: Number of non-zero elements in f • Let • When is where ? where and K(A) is the largest integer such that any set of K(A) columns of A is linearly independent. • Thm. 1: Unique l 0 solution • What can we say about more tractable formulations like l 1 ?

Stochastic Systems Group l 1 equivalence conditions • Consider the l 1 problem: • Can we ever hope to get ? • Thm. 2(*): • where is sparse enough exact solution by l 1 optimization l 1 solution = l 0 solution ! • Can solve a combinatorial optimization problem by convex optimization! (*) Donoho and Elad obtained a similar result concurrently.

Stochastic Systems Group lp (p ≤ 1) equivalence conditions • Consider the lp problem: • How about ? • Thm. 3: where lp solution = l 0 solution ! Smaller p • Smaller p more non-zero elements tolerated • As p 0 we recover the l 0 condition, namely

Stochastic Systems Group l 0 uniqueness conditions • Prefer the sparsest solution: Number of non-zero elements in f • Let • When is • ? Definition: The index of ambiguity K(A) of A is the largest integer such that any set of K(A) columns of A is linearly independent. • Thm. 1: Unique l 0 solution • What can we say about more tractable formulations like l 1 ?

Stochastic Systems Group l 1 equivalence conditions • Consider the l 1 problem: • Can we ever hope to get • Definition: Maximum absolute dot product of columns ? • Thm. 2(*): • is sparse enough exact solution by l 1 optimization l 1 solution = l 0 solution ! • Can solve a combinatorial optimization problem by convex optimization! (*) Donoho and Elad obtained a similar result concurrently.

Stochastic Systems Group lp (p ≤ 1) equivalence conditions • Consider the lp problem: • How about • Definition: ? • Thm. 3: lp solution = l 0 solution ! Smaller p • Smaller p more non-zero elements tolerated • As p 0 we recover the l 0 condition, namely