Stochastic Roadmap Simulation An efficient representation and algorithm

Stochastic Roadmap Simulation: An efficient representation and algorithm for analyzing molecular motion Mehmet Serkan Apaydιn May 27 th, 2004

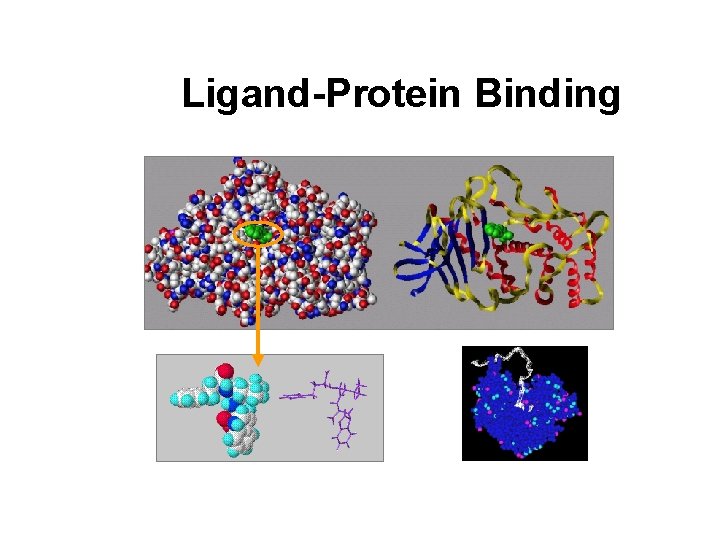
Molecular motion is an essential process of life Bovine Spongiform Encephalopathy (BSE) http: //www. usd. edu/eric/ protein (mis)-folding An NMR spectrometer (CS 273) Drug molecules act by binding to proteins http: //www. the-scientist. com Ligand-protein binding Stanford bio-x cluster

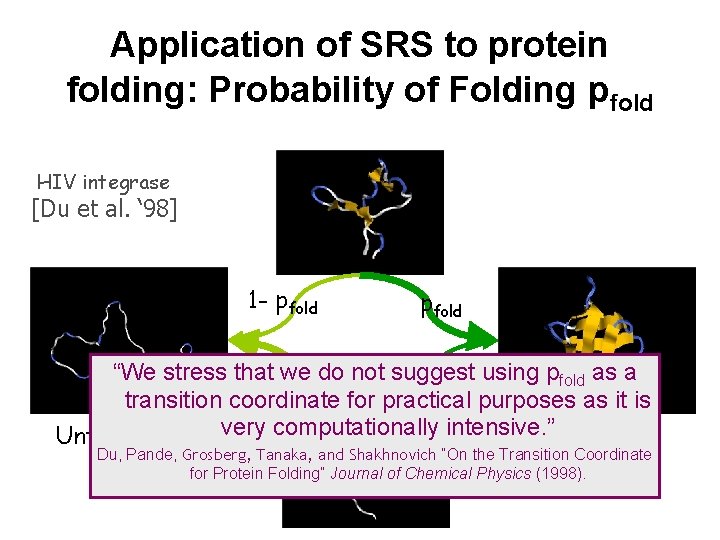
Computing pfold, the best order parameter in protein folding is expensive using classical simulation techniques HIV integrase [Du et al. ‘ 98] 1 - pfold “We stress that we do not suggest using pfold as a transition coordinate for practical purposes as it is Folded set Unfolded set very computationally intensive. ” Du, Pande, Grosberg, Tanaka, and Shakhnovich “On the Transition Coordinate for Protein Folding” Journal of Chemical Physics (1998).

Stochastic Roadmap Simulation (SRS) Develop efficient computational representations and algorithms to study molecular motion pathways for protein folding and ligand-protein binding

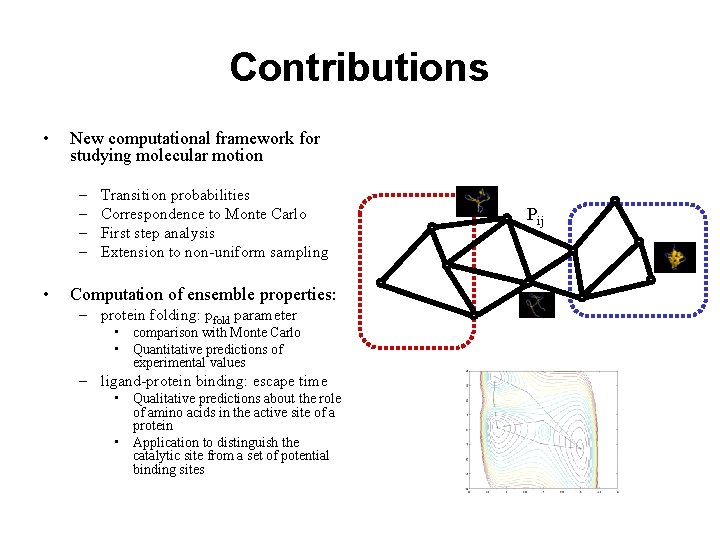
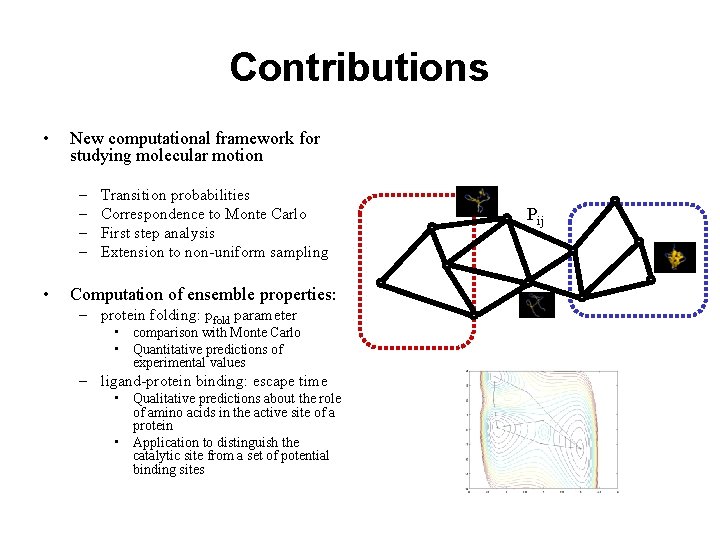
Contributions • New computational framework for studying molecular motion – – • Transition probabilities Correspondence to Monte Carlo First step analysis Extension to non-uniform sampling Computation of ensemble properties: – protein folding: pfold parameter • comparison with Monte Carlo • Quantitative predictions of experimental values – ligand-protein binding: escape time • Qualitative predictions about the role of amino acids in the active site of a protein • Application to distinguish the catalytic site from a set of potential binding sites Pij

Outline • Background • Stochastic Roadmap Simulation • Applications – Protein folding – Ligand-protein binding • Extension of basic framework • Quantitative prediction of experimental results on protein folding

Proteins and their structure • Macromolecule • Building block of life.

Ligand-Protein Binding

Simulating molecular motion • Monte Carlo (MC) or Molecular Dynamics http: //folding. stanford. edu

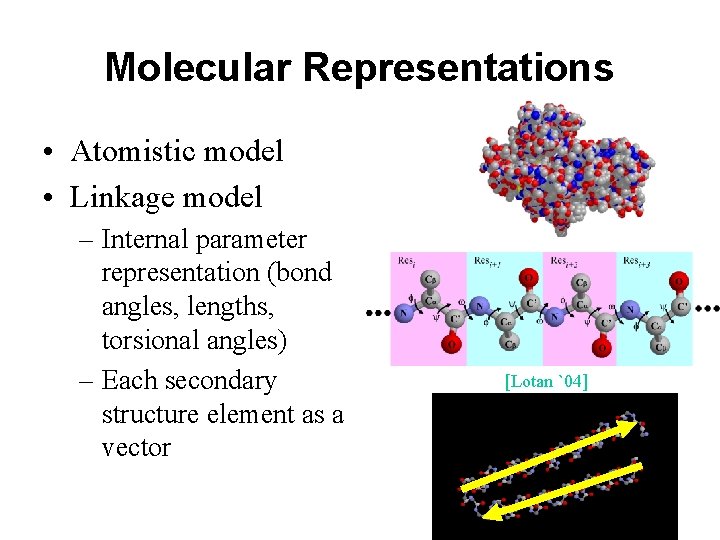
Molecular Representations • Atomistic model • Linkage model – Internal parameter representation (bond angles, lengths, torsional angles) – Each secondary structure element as a vector [Lotan `04]

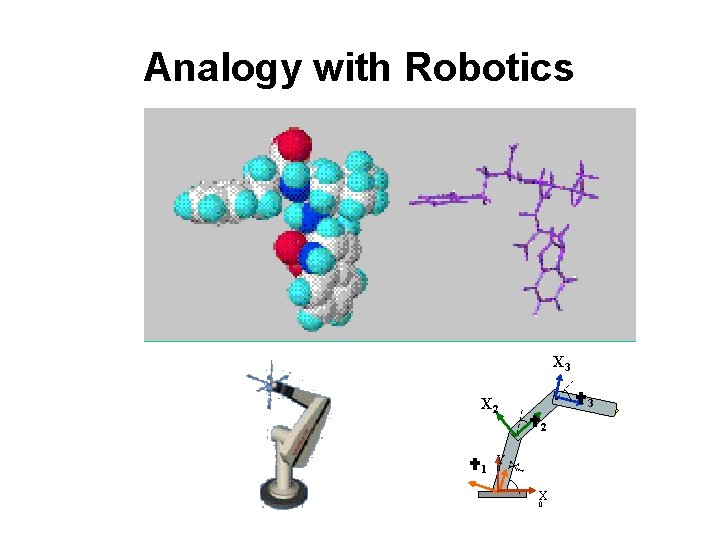
Analogy with Robotics X 3 3 X 2 0 X Y 1 1 2 X 0

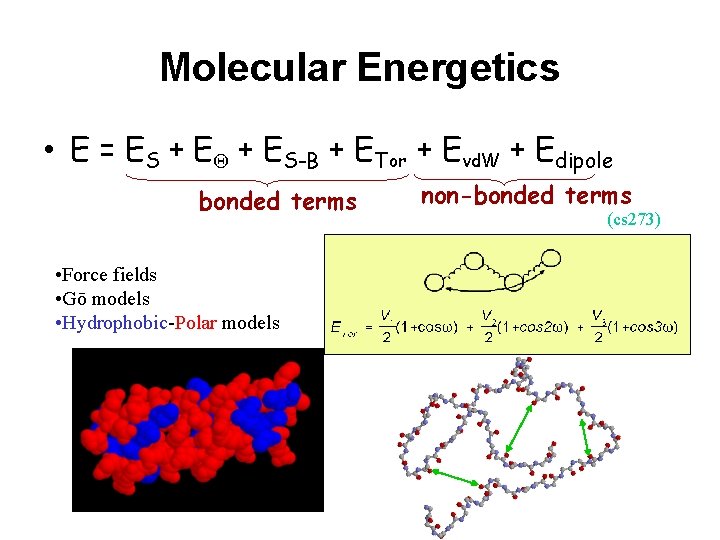
Molecular Energetics • E = ES + EQ + ES-B + ETor + Evd. W + Edipole bonded terms • Force fields • Gō models • Hydrophobic-Polar models non-bonded terms (cs 273)

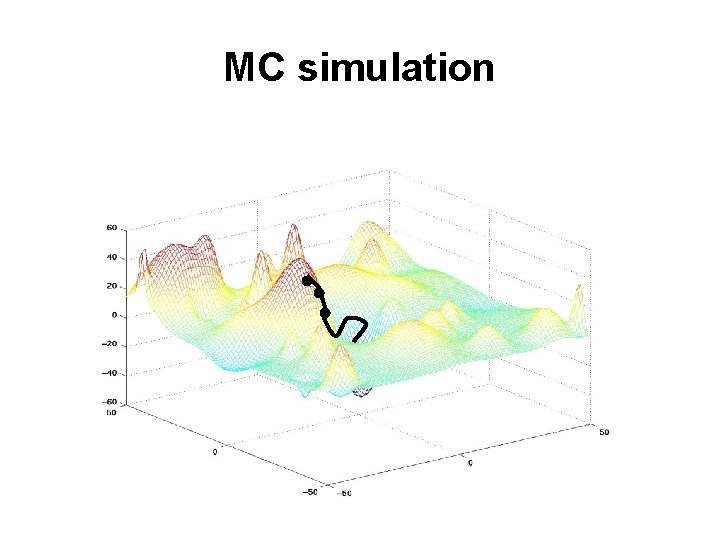
MC simulation

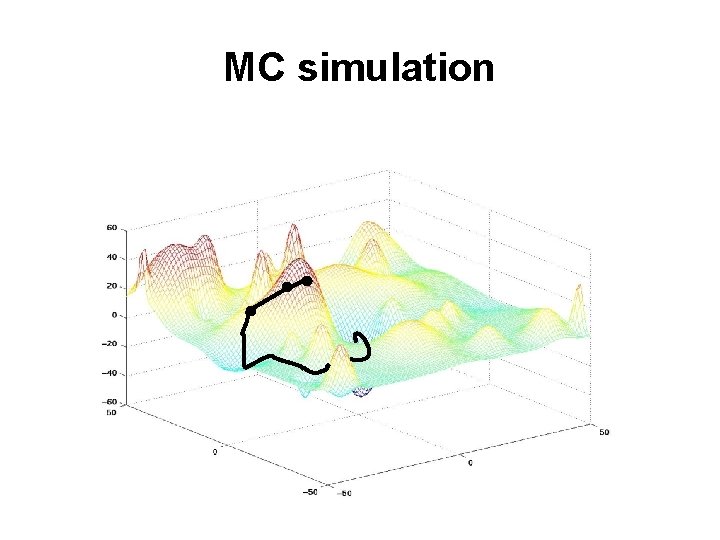
MC simulation

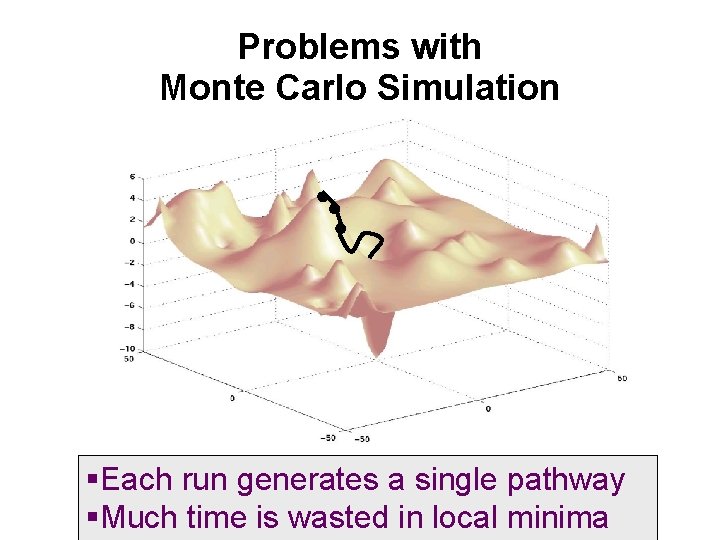
Problems with Monte Carlo Simulation Each run generates a single pathway Much time is wasted in local minima

A path planning technique: Probabilistic Roadmaps (PRM) [Kavraki et. al. `96] Configuration space Qgoal edge Qinit C-obstacle node Preprocessing Query

Application of PRM to molecular motion • Study of ligand-protein binding • Probabilistic roadmaps with edges weighted by energetic plausibility • Search for the minimum weight paths [Singh, Latombe, Brutlag, `99]

Application of PRM to molecular motion • Study of ligand-protein binding • Probabilistic roadmaps with edges weighted by energetic plausibility • Search for the minimum weight paths • Extensions to protein folding [Song and Amato, `01] [Apaydın et al. , `01] [Singh, Latombe, Brutlag, `99]

How many pathways are there in a roadmap? Number of Self-Avoiding Walks on a 2 D Grid 1, 2, 184, 8512, 1262816, 575780564, 789360053252, 3266598486981642, (10 x 10) 41044208702632496804, (11 x 11) 1568758030464750013214100, (12 x 12) 182413291514248049241470885236 n/m 2 2 2 3 4 12 4 8 38 184 5 16 125 976 8512 6 32 414 5382 79384 3 http: //mathworld. wolfram. com/Self-Avoiding. Walk. html 4 5 6 1262816

Outline • Background • Stochastic Roadmap Simulation • Applications – Protein folding – Ligand-protein binding • Future work

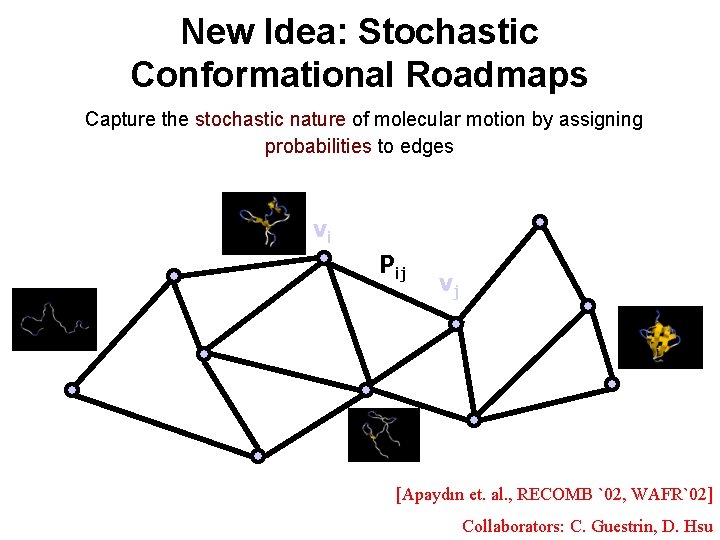
New Idea: Stochastic Conformational Roadmaps Capture the stochastic nature of molecular motion by assigning probabilities to edges vi Pij vj [Apaydın et. al. , RECOMB `02, WAFR`02] Collaborators: C. Guestrin, D. Hsu

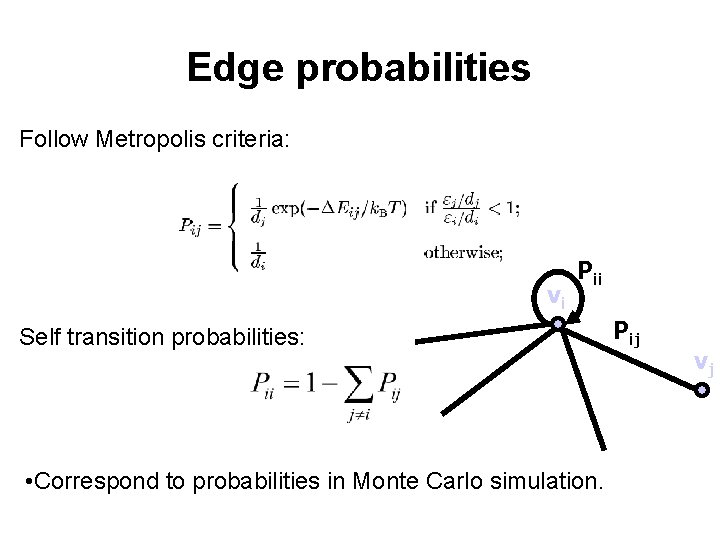
Edge probabilities Follow Metropolis criteria: vi Pii Self transition probabilities: • Correspond to probabilities in Monte Carlo simulation. Pij vj

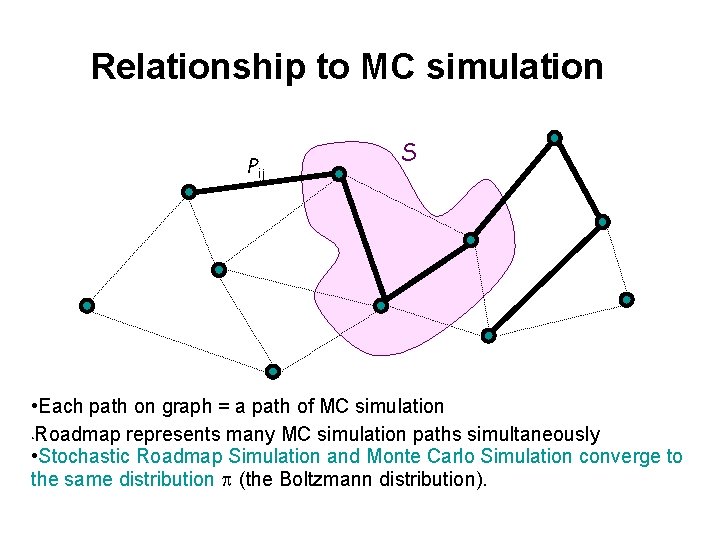
Relationship to MC simulation Pij S • Each path on graph = a path of MC simulation • Roadmap represents many MC simulation paths simultaneously • Stochastic Roadmap Simulation and Monte Carlo Simulation converge to the same distribution (the Boltzmann distribution).

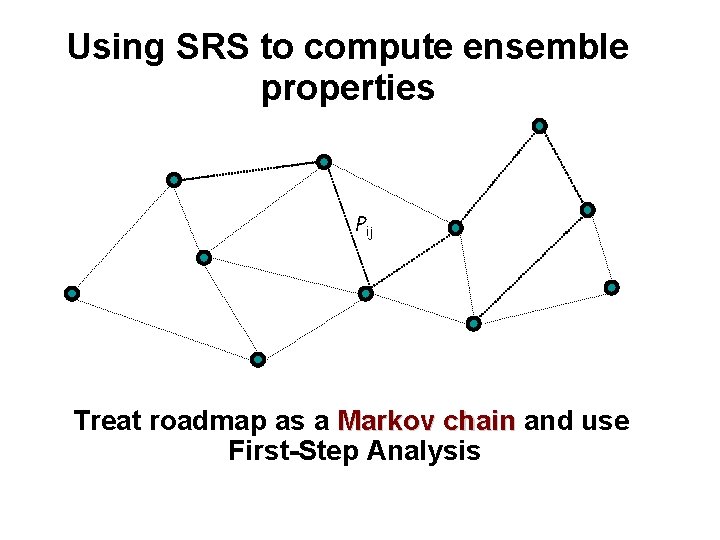
Using SRS to compute ensemble properties Pij Treat roadmap as a Markov chain and use First-Step Analysis

Application of SRS to protein folding: Probability of Folding pfold HIV integrase [Du et al. ‘ 98] 1 - pfold “We stress that we do not suggest using pfold as a transition coordinate for practical purposes as it is Folded set Unfolded set very computationally intensive. ” Du, Pande, Grosberg, Tanaka, and Shakhnovich “On the Transition Coordinate for Protein Folding” Journal of Chemical Physics (1998).

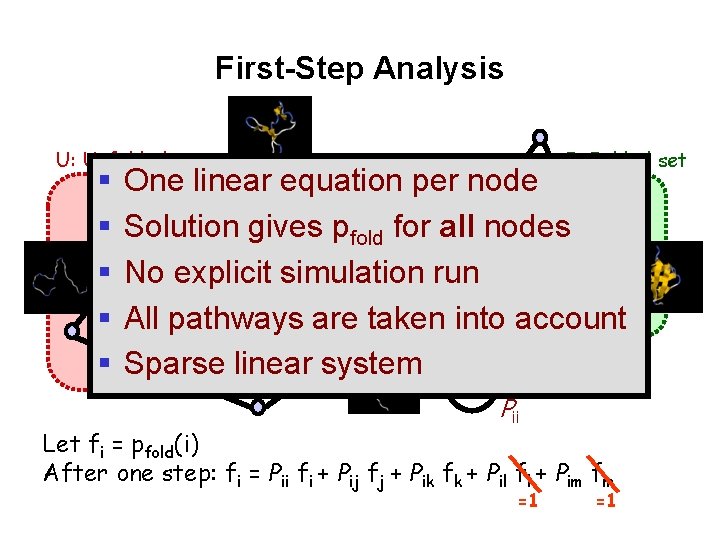
First-Step Analysis U: Unfolded set F: Folded set One linear equation per node Solution gives pfold for all nodes l k No explicit simulation run j Pik Pil All pathways are taken Pij into account m Pim Sparse linear system i Pii Let fi = pfold(i) After one step: fi = Pii fi + Pij fj + Pik fk + Pil fl + Pim fm =1 =1

In Contrast … Computing pfold with MC simulation requires: Performing many MC simulation runs Counting the number of times F is attained first for every conformation of interest:

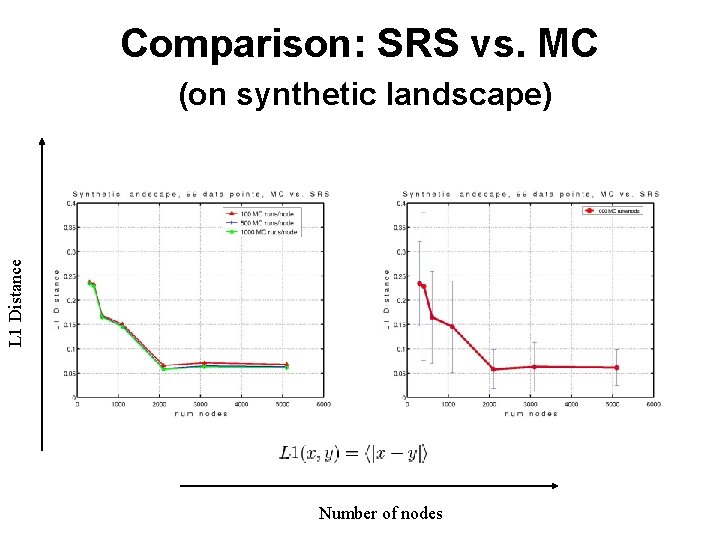
Comparison: SRS vs. MC L 1 Distance (on synthetic landscape) Number of nodes

Computational Tests on two real proteins • 1 ROP (repressor of primer) • 2 helices • 6 DOF • 1 HDD (Engrailed homeodomain) • 3 helices • 12 DOF H-P energy model with steric clash exclusion [Sun et al. , `95]

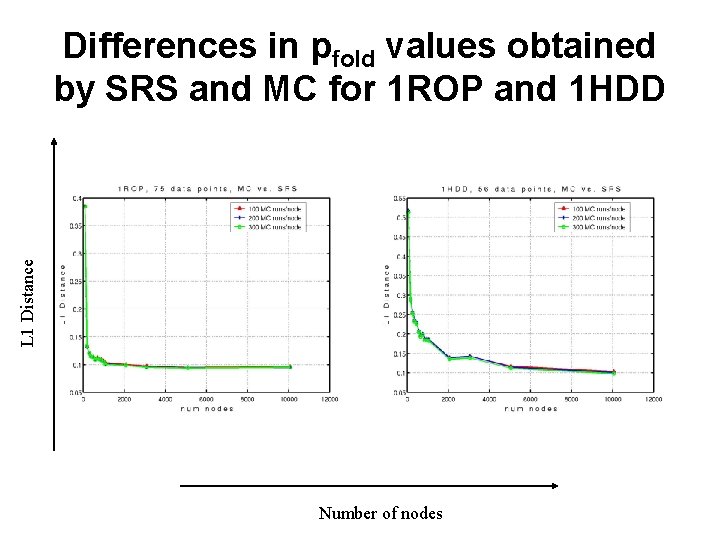
L 1 Distance Differences in pfold values obtained by SRS and MC for 1 ROP and 1 HDD Number of nodes

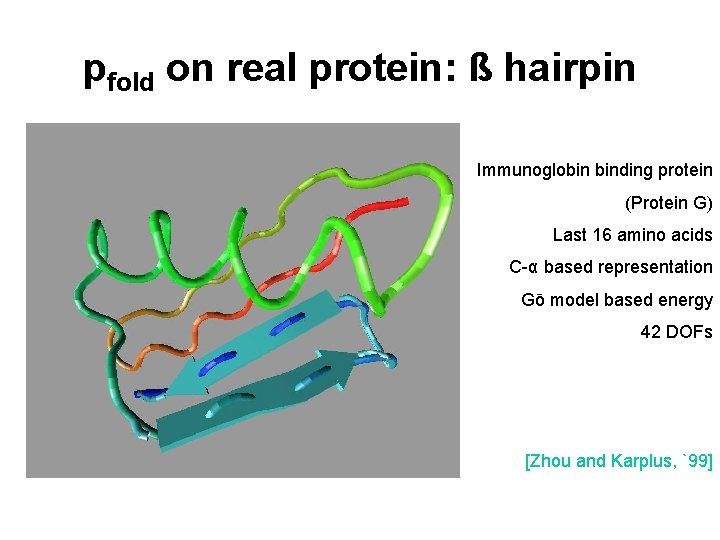
pfold on real protein: ß hairpin Immunoglobin binding protein (Protein G) Last 16 amino acids C-α based representation Gō model based energy 42 DOFs [Zhou and Karplus, `99]

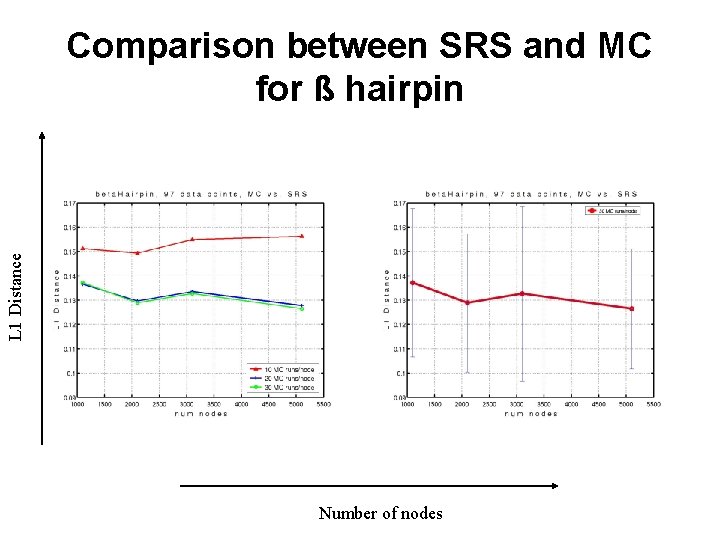
L 1 Distance Comparison between SRS and MC for ß hairpin Number of nodes

Computation Times (ß hairpin) Monte Carlo: (30 simulations) 1 conformation ~10 hours of computer time Over 107 energy computations 23 seconds of computer time ~50, 000 energy computations Roadmap: 2000 conformations ~6 orders of magnitude speedup!

Outline • Background • Stochastic Roadmap Simulation • Applications – Protein folding – Ligand-protein binding • Extension of basic framework • Quantitative prediction of experimental results on protein folding

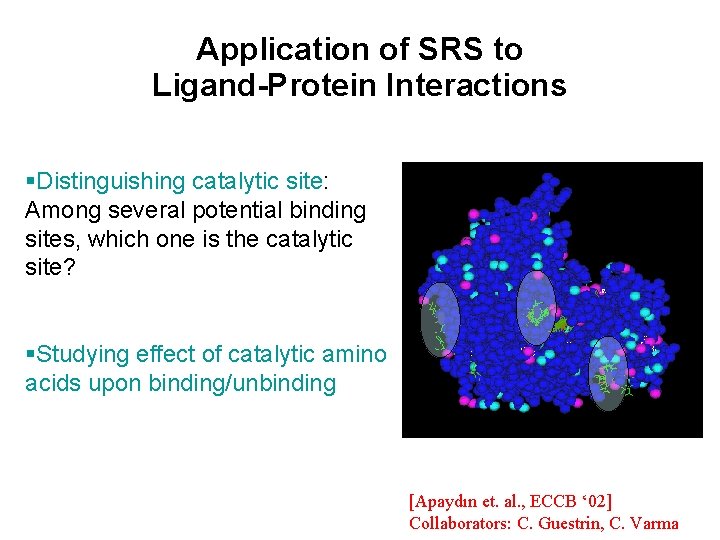
Application of SRS to Ligand-Protein Interactions Distinguishing catalytic site: Among several potential binding sites, which one is the catalytic site? Studying effect of catalytic amino acids upon binding/unbinding [Apaydın et. al. , ECCB ‘ 02] Collaborators: C. Guestrin, C. Varma

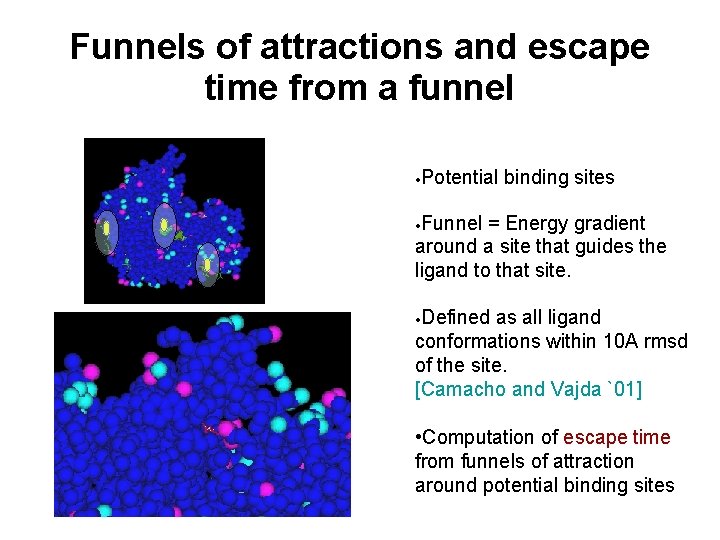
Funnels of attractions and escape time from a funnel • Potential binding sites • Funnel = Energy gradient around a site that guides the ligand to that site. • Defined as all ligand conformations within 10 A rmsd of the site. [Camacho and Vajda `01] • Computation of escape time from funnels of attraction around potential binding sites

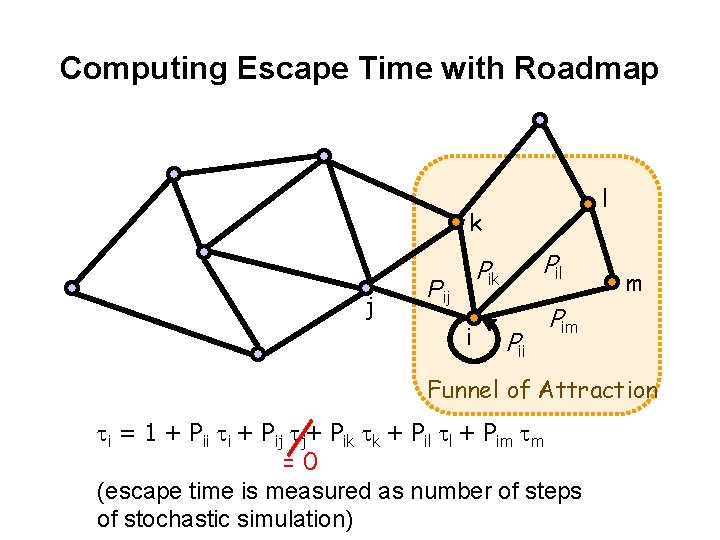
Computing Escape Time with Roadmap l k j Pil Pik Pij i Pii m Pim Funnel of Attraction ti = 1 + Pii ti + Pij tj+ Pik tk + Pil tl + Pim tm =0 (escape time is measured as number of steps of stochastic simulation)

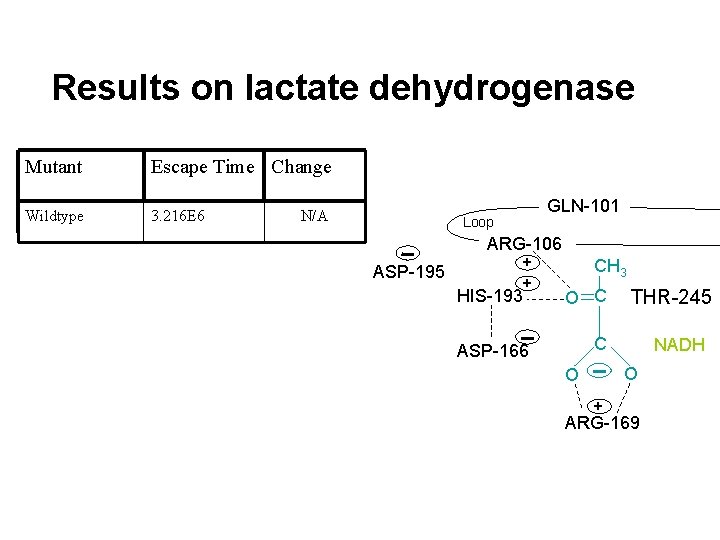
Results on lactate dehydrogenase Mutant Escape Time Change Wildtype 3. 216 E 6 N/A GLN-101 Loop ARG-106 ASP-195 + + HIS-193 CH 3 O C THR-245 C ASP-166 NADH O O + ARG-169

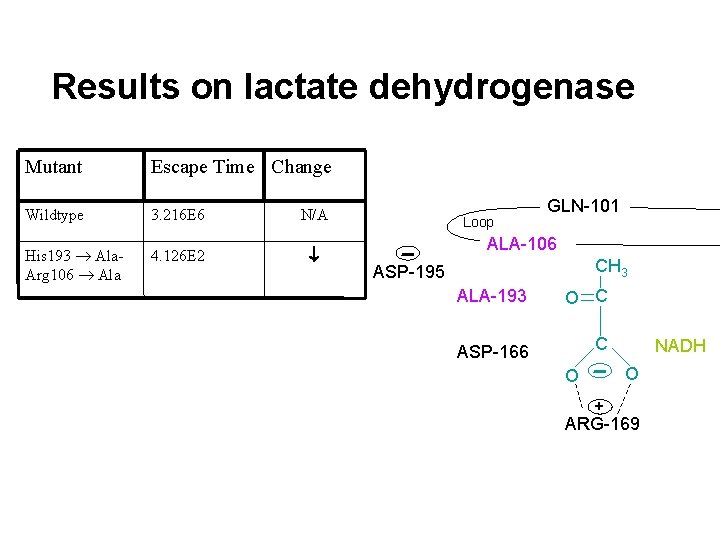
Results on lactate dehydrogenase Mutant Escape Time Change Wildtype 3. 216 E 6 N/A His 193 Ala. Arg 106 Ala 4. 126 E 2 Loop GLN-101 ALA-106 CH 3 ASP-195 ALA-193 O C ASP-166 C NADH O O + ARG-169

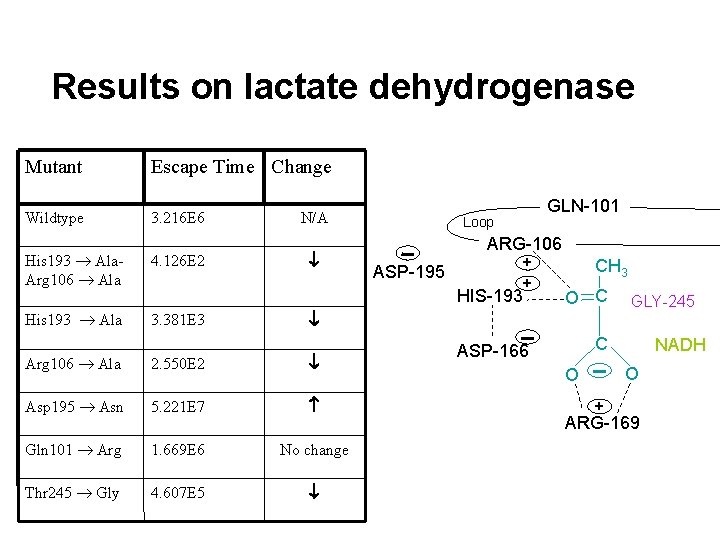
Results on lactate dehydrogenase Mutant Escape Time Change Wildtype 3. 216 E 6 His 193 Ala. Arg 106 Ala His 193 Ala 4. 126 E 2 N/A GLN-101 Loop ARG-106 ASP-195 + + HIS-193 3. 381 E 3 CH 3 O C Arg 106 Ala 2. 550 E 2 Asp 195 Asn 5. 221 E 7 Gln 101 Arg 1. 669 E 6 No change Thr 245 Gly 4. 607 E 5 GLY-245 C ASP-166 NADH O O + ARG-169

Outline • Background • Stochastic Roadmap Simulation • Applications – Protein folding – Ligand-protein binding • Extension of basic framework • Quantitative prediction of experimental results on protein folding

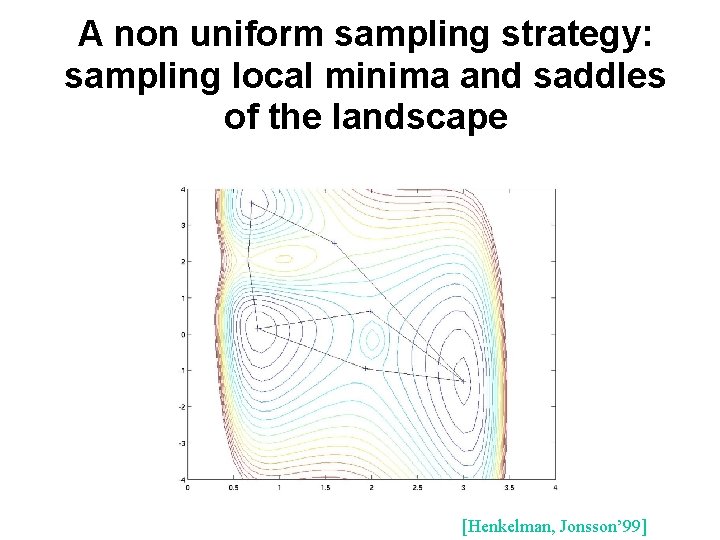
A non uniform sampling strategy: sampling local minima and saddles of the landscape [Henkelman, Jonsson’ 99]

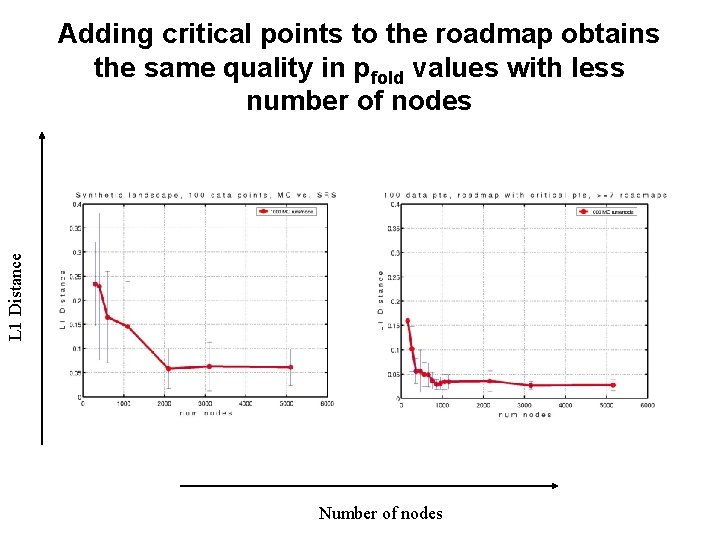
L 1 Distance Adding critical points to the roadmap obtains the same quality in pfold values with less number of nodes Number of nodes

Outline • Background • Stochastic Roadmap Simulation • Applications – Protein folding – Ligand-protein binding • Extension of basic framework • Quantitative prediction of experimental results on protein folding

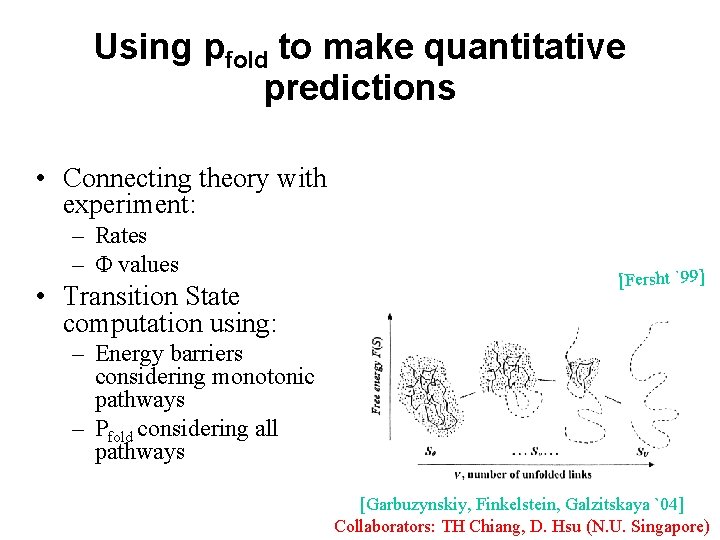
Using pfold to make quantitative predictions • Connecting theory with experiment: – Rates – Φ values • Transition State computation using: [Fersht `99] – Energy barriers considering monotonic pathways – Pfold considering all pathways [Garbuzynskiy, Finkelstein, Galzitskaya `04] Collaborators: TH Chiang, D. Hsu (N. U. Singapore)

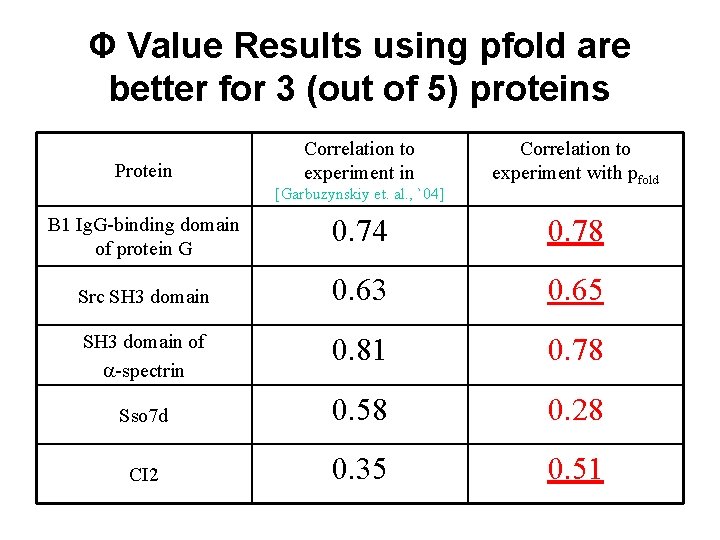
Φ Value Results using pfold are better for 3 (out of 5) proteins Protein Correlation to experiment in [Garbuzynskiy et. al. , `04] Correlation to experiment with pfold B 1 Ig. G-binding domain of protein G 0. 74 0. 78 Src SH 3 domain 0. 63 0. 65 SH 3 domain of -spectrin 0. 81 0. 78 Sso 7 d 0. 58 0. 28 CI 2 0. 35 0. 51

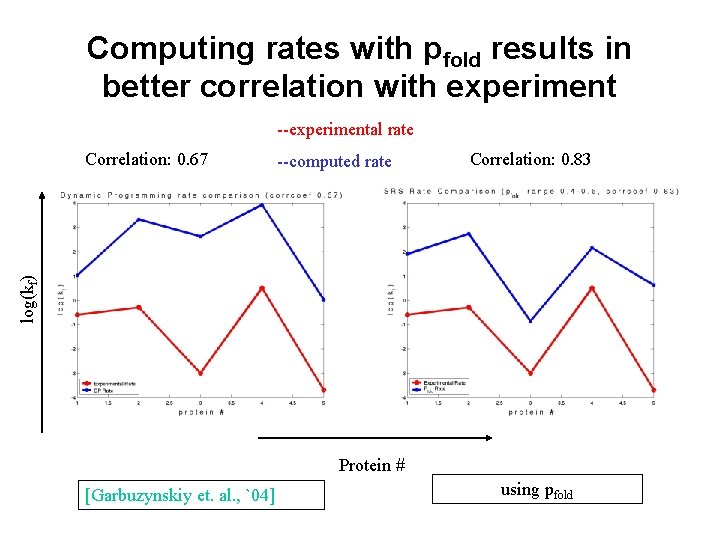
Computing rates with pfold results in better correlation with experiment --experimental rate --computed rate Correlation: 0. 83 log(kf) Correlation: 0. 67 Protein # [Garbuzynskiy et. al. , `04] using pfold

Contributions • New computational framework for studying molecular motion – – • Transition probabilities Correspondence to Monte Carlo First step analysis Extension to non-uniform sampling Computation of ensemble properties: – protein folding: pfold parameter • comparison with Monte Carlo • Quantitative predictions of experimental values – ligand-protein binding: escape time • Qualitative predictions about the role of amino acids in the active site of a protein • Application to distinguish the catalytic site from a set of potential binding sites Pij

Future work • Non-uniform sampling on high-dimensional examples • Computing and reducing the error in the computed parameters • Estimating the number of nodes needed • Exploring larger systems and pushing the experiment q 2 q 5 q 3 q 1 q 4

SRS code available! Visit: http: //robotics. stanford. edu/~apaydin/software. html

Acknowledgements My advisors: Prof. Latombe, Prof. Brutlag Prof. Van Roy Prof. Mc. Cluskey My committee: Prof. Motwani, Prof. Vuckovic Coauthors: D. Hsu, C. Guestrin, S. Kasif, A. Singh, C. Varma Collaborators: TH Chiang, J. Greenberg, S. Ieong, F. Schwarzer, R. Singh, A. Tellez Faculty: Prof. Altman, Prof. Baldwin, Prof. Guibas, Prof. Pande Prof. Kavraki (Rice) Prof. Zell (Tuebingen) Prof. Snoeyink (UNC) Funding: David L. Cheriton Stanford Graduate Fellowship NSF Biogeometry grant Stanford’s Bio-X program Resources: Bio-X SGI Supercomputer, Bio-X PC computer cluster Colleagues: N. Batada, A. Ben-Hur, S. Bennett, E. Boas, T. Bretl, J. Brown, F. Buron, L. Chong, A. Collins, S. Elmer, P. Fong, A. Garg, S. Gokturk, H. Gonzales. Banos, K. Hauser, G. Henkelman, P. Isto, G. Jayachandran, J. Kuffner, S. Larson, M. Liang, B. Naughton, X. Liu, I. Lotan, H. Mandyam, N. Mitra, S. Mitra, A. Nguyen, YM Rhee, D. Russel, M. Saha, G. Sanchez-Ante, S. Saxonov, S. Schmidler, J. Shapiro, J. Shin, P. Shirvani, M. Shirts, C. Snow, C. Yu, B. Zagrovic, A. Zomorodian Staff: I. Contreras, P. Cook, J. Engelson, K. Hedjasi, J. Mc. Cormick, H. Nguyen, N. Riewerts, D. Shankle Friends and family

Thank you!