Stochastic quantum dynamics beyond meanfield Denis Lacroix Laboratoire
Stochastic quantum dynamics beyond mean-field. Denis Lacroix Laboratoire de Physique Corpusculaire - Caen, FRANCE e One Body spac Introduction to stochastic TDHF Application to collective motions Alternative exact stochastic mechanics Functional integrals for dynamical Many-body problems
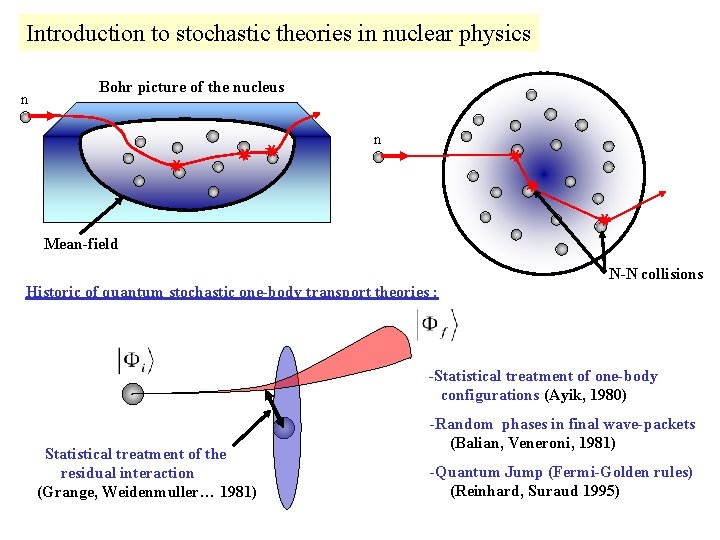
Introduction to stochastic theories in nuclear physics n Bohr picture of the nucleus n Mean-field N-N collisions Historic of quantum stochastic one-body transport theories : -Statistical treatment of one-body configurations (Ayik, 1980) Statistical treatment of the residual interaction (Grange, Weidenmuller… 1981) -Random phases in final wave-packets (Balian, Veneroni, 1981) -Quantum Jump (Fermi-Golden rules) (Reinhard, Suraud 1995)

Introduction to stochastic mean-field theories : D. Lacroix, S. Ayik and Ph. Chomaz, Progress in Part. and Nucl. Phys. (2004) Starting from : { The correlation propagates as : where { Propagated initial correlation Two-body effect projected on the one-body space
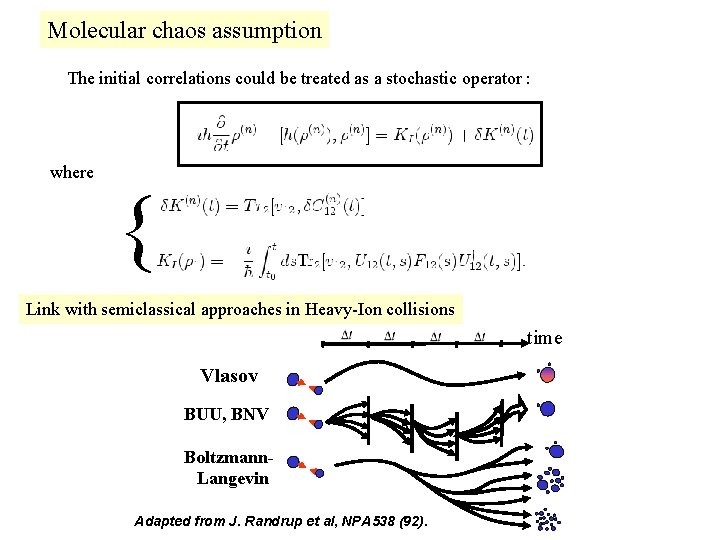
Molecular chaos assumption The initial correlations could be treated as a stochastic operator : where { Link with semiclassical approaches in Heavy-Ion collisions time Vlasov BUU, BNV Boltzmann. Langevin Adapted from J. Randrup et al, NPA 538 (92).
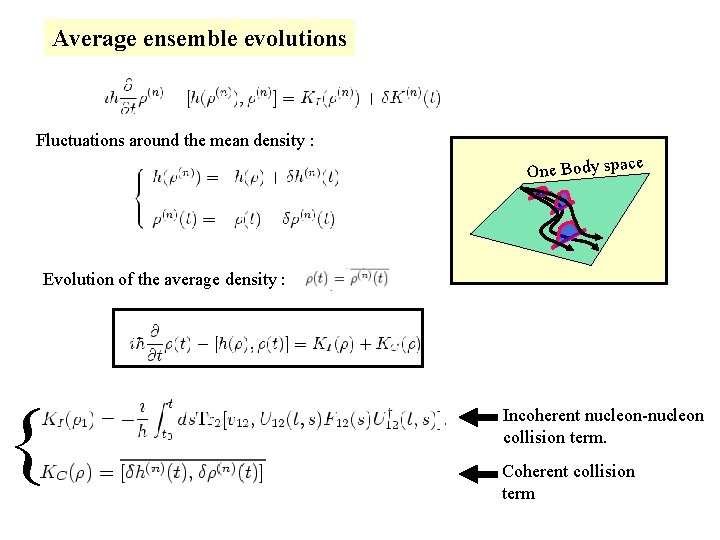
Average ensemble evolutions Fluctuations around the mean density : e One Body spac Evolution of the average density : { Incoherent nucleon-nucleon collision term. Coherent collision term
Application to small amplitude motion Standard RPA states Coupling to 2 p 2 h states Coupling to ph-phonon
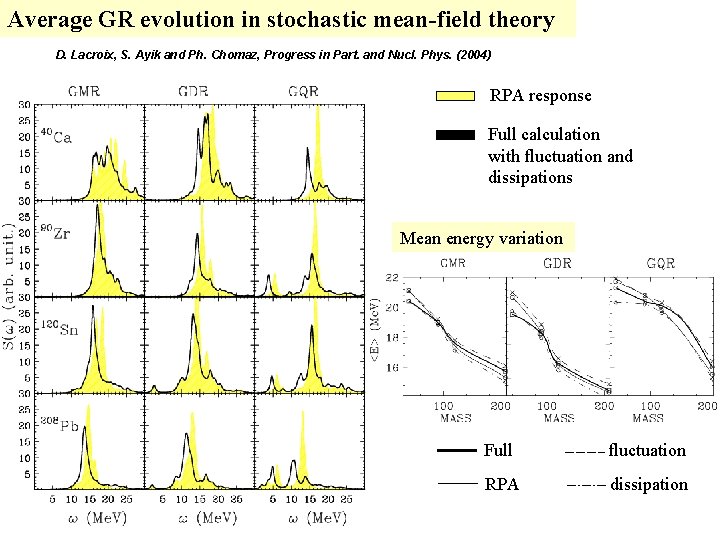
Average GR evolution in stochastic mean-field theory D. Lacroix, S. Ayik and Ph. Chomaz, Progress in Part. and Nucl. Phys. (2004) RPA response Full calculation with fluctuation and dissipations Mean energy variation Full fluctuation RPA dissipation
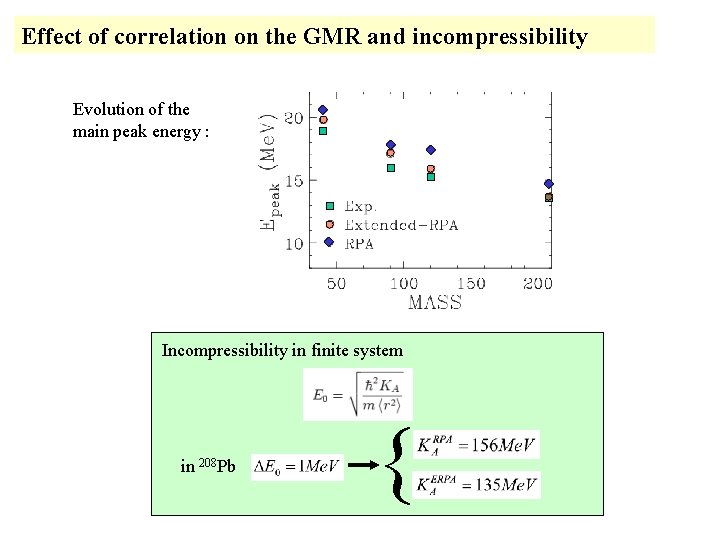
Effect of correlation on the GMR and incompressibility Evolution of the main peak energy : Incompressibility in finite system in 208 Pb {
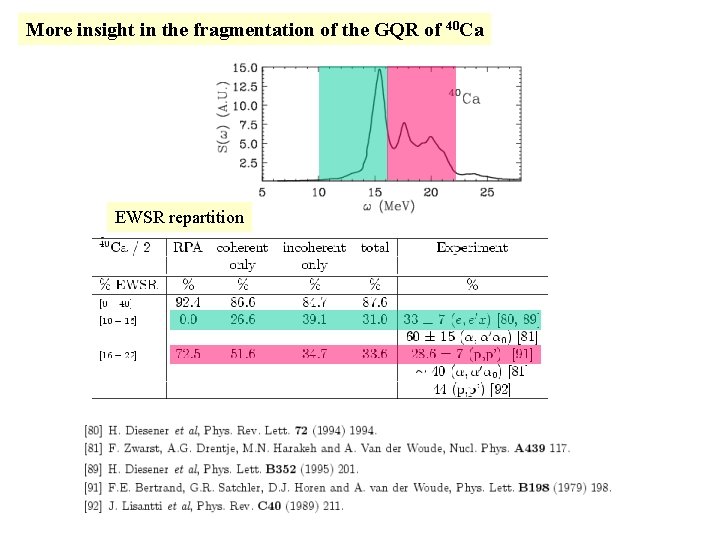
More insight in the fragmentation of the GQR of 40 Ca EWSR repartition
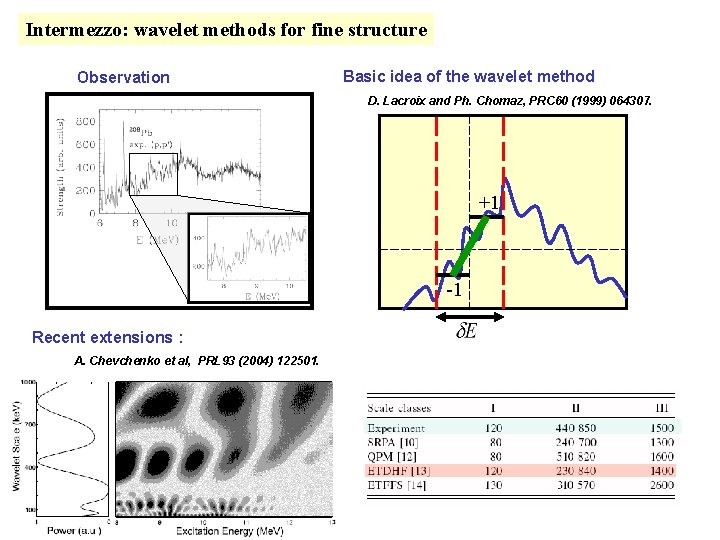
Intermezzo: wavelet methods for fine structure Observation Basic idea of the wavelet method D. Lacroix and Ph. Chomaz, PRC 60 (1999) 064307. +1 -1 Recent extensions : A. Chevchenko et al, PRL 93 (2004) 122501.

Discussion on approximate quantum stochastic theories based on statistical assumptions Success Results on small amplitude motions looks fine The semiclassical version (BOB) gives a good reproduction of Heavy-Ion collisions Critical aspects Stochastic methods for large amplitude motion are still an open problem (No guide to the random walk) Instantaneous reorganization of internal degrees of freedom? Which interaction for the collision term Theoretical justification of the introduction of noise

Functional integral and stochastic quantum mechanics General strategy S. Levit, PRCC 21 (1980) 1594. S. E. Koonin, D. J. Dean, K. Langanke, Ann. Rev. Nucl. Part. Sci. 47, 463 (1997). Given a Hamiltonian and an initial State Write H into a quadratic form Use the Hubbard Stratonovich transformation Interpretation of the integral in terms of quantum jumps and stochastic Schrödinger equation time Example of application: -Quantum Monte-Carlo Methods -Shell Model Monte-Carlo. . .
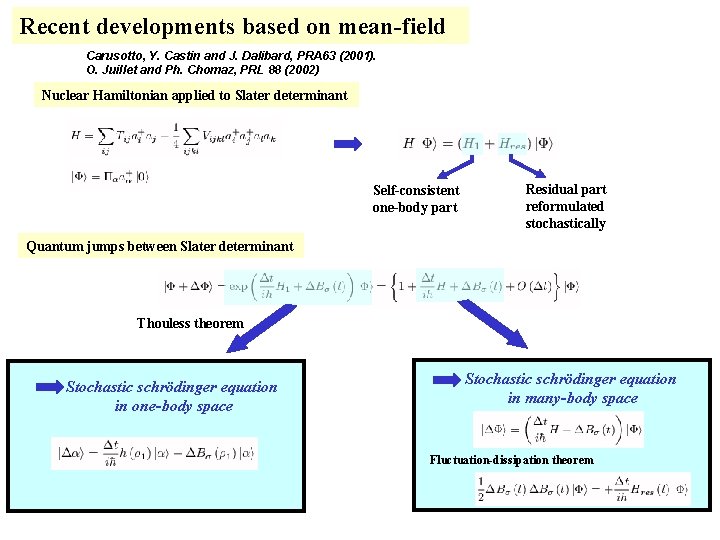
Recent developments based on mean-field Carusotto, Y. Castin and J. Dalibard, PRA 63 (2001). O. Juillet and Ph. Chomaz, PRL 88 (2002) Nuclear Hamiltonian applied to Slater determinant Self-consistent one-body part Residual part reformulated stochastically Quantum jumps between Slater determinant Thouless theorem Stochastic schrödinger equation in one-body space Stochastic schrödinger equation in many-body space Fluctuation-dissipation theorem
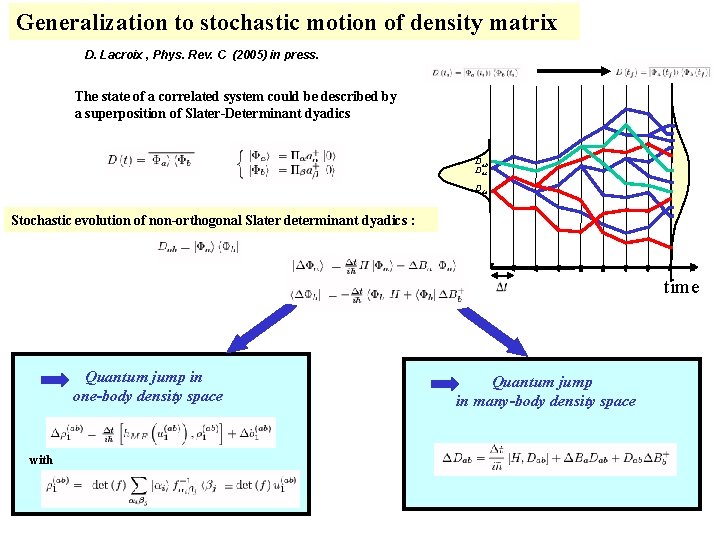
Generalization to stochastic motion of density matrix D. Lacroix , Phys. Rev. C (2005) in press. The state of a correlated system could be described by a superposition of Slater-Determinant dyadics Dab Dac Dde Stochastic evolution of non-orthogonal Slater determinant dyadics : time Quantum jump in one-body density space with Quantum jump in many-body density space

Discussion of exact quantum jump approaches Many-Body Stochastic Schrödinger equation One-Body Stochastic Schrödinger equation Generalization : Stochastic evolution of many-body density Stochastic evolution of one-body density Each time the two-body density evolves as : with Then, the evolution of the two-body density can be replaced by an average ( stochastic one-body evolution with : Actual applications : -Bose-condensate -Two and three-level systems -Spin systems (Carusotto et al, PRA (2001)) (Juillet et al, PRL (2002)) (Lacroix, PRA (2005)) ) of

Exact stochastic dynamics guiding approximate quantum stochastic mechanics Weak coupling approximation : perturbative treatment Residual interaction in the mean-field interaction picture Statistical assumption in the quasi-Markovian limit : We assume that the residual interaction can be treated as An ensemble of two-body interaction:
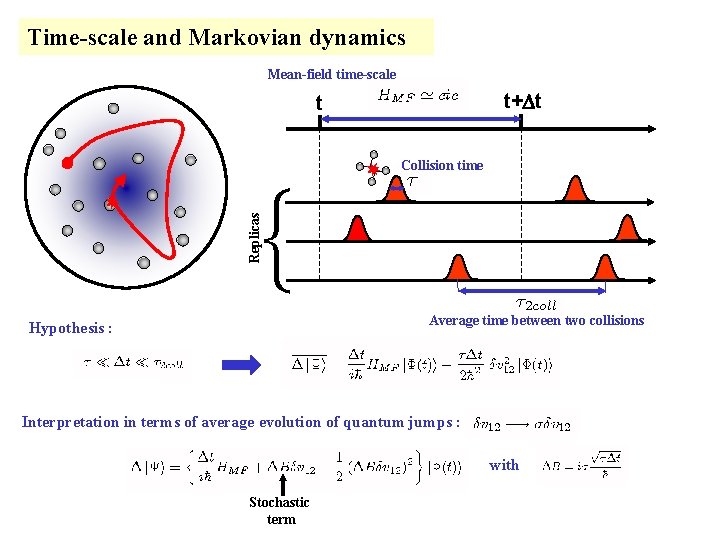
Time-scale and Markovian dynamics Mean-field time-scale t+Dt t Collision time Replicas { Average time between two collisions Hypothesis : Interpretation in terms of average evolution of quantum jumps : with Stochastic term

From stochastic many-body to stochastic one-body evolution We need additional simplification e One Body spac Following approximate dynamics We focus on one-body degrees of freedom Following the exact stochastic dynamics We introduce the density Gaussian approximation for quantal fluctuations We obtain a new stochastic one-body evolution in the perturbative regime: D. Lacroix, in preparation (2005) Mean-field like term

Perturbative/Exact stochastic evolution Exact Perturbative Properties Many-body density Projector Number of particles Entropy Average evolution One-body Correlations beyond mean-field Numerical implementation : Flexible: one stoch. Number or more… Fixed : “s” determines the number of stoch. variables
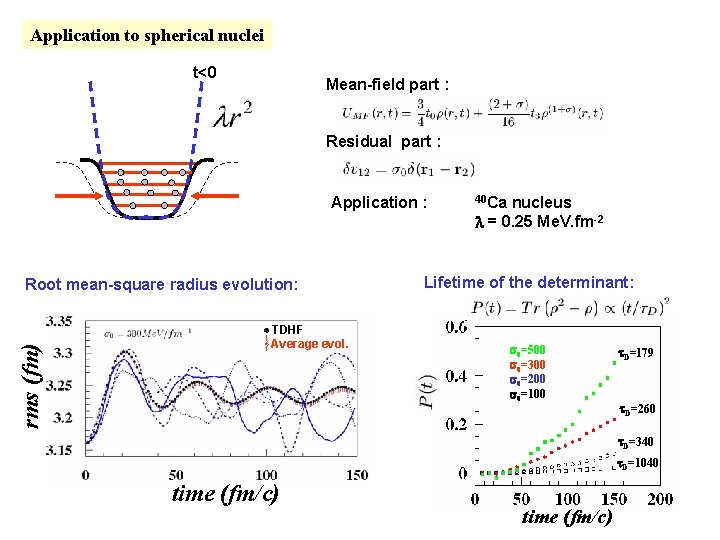
Application to spherical nuclei t<0 Mean-field part : Residual part : Application : rms (fm) Root mean-square radius evolution: TDHF Average evol. 40 Ca nucleus l = 0. 25 Me. V. fm-2 Lifetime of the determinant: s 0=500 s 0=300 s 0=200 s 0=100 t. D=179 t. D=260 t. D=340 t. D=1040 time (fm/c)
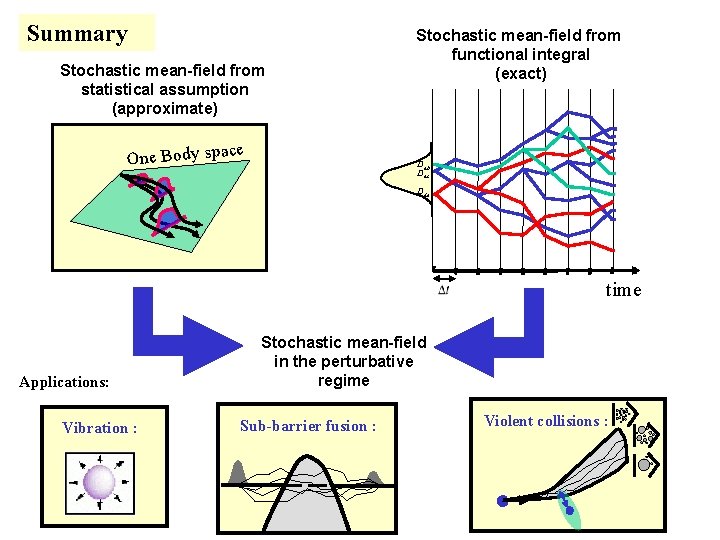
Summary Stochastic mean-field from statistical assumption (approximate) Stochastic mean-field from functional integral (exact) e One Body spac Dab Dac Dde time Applications: Vibration : Stochastic mean-field in the perturbative regime Sub-barrier fusion : Violent collisions :
- Slides: 21