Stochastic processes Lecture 8 Ergodicty 1 Random process

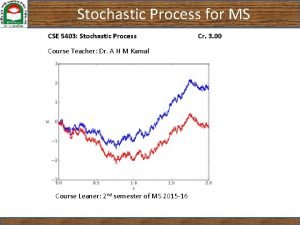
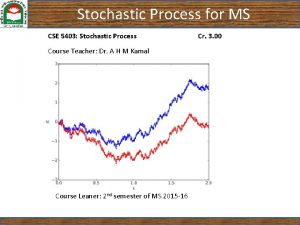
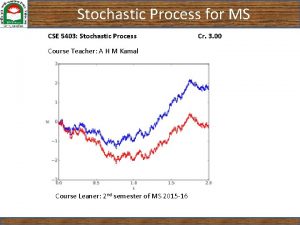
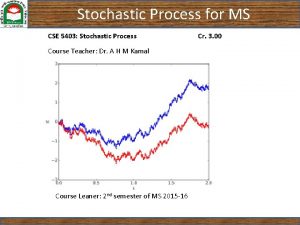
Stochastic processes Lecture 8 Ergodicty 1

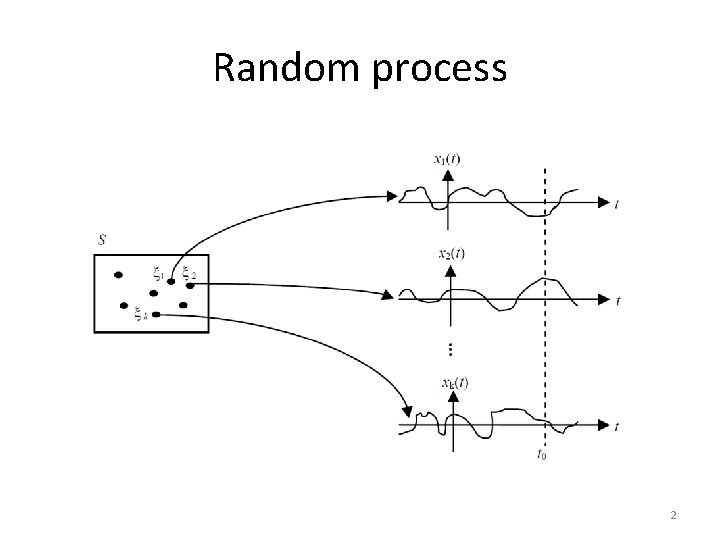
Random process 2

3

Agenda (Lec. 8) • Ergodicity • Central equations • Biomedical engineering example: – Analysis of heart sound murmurs 4

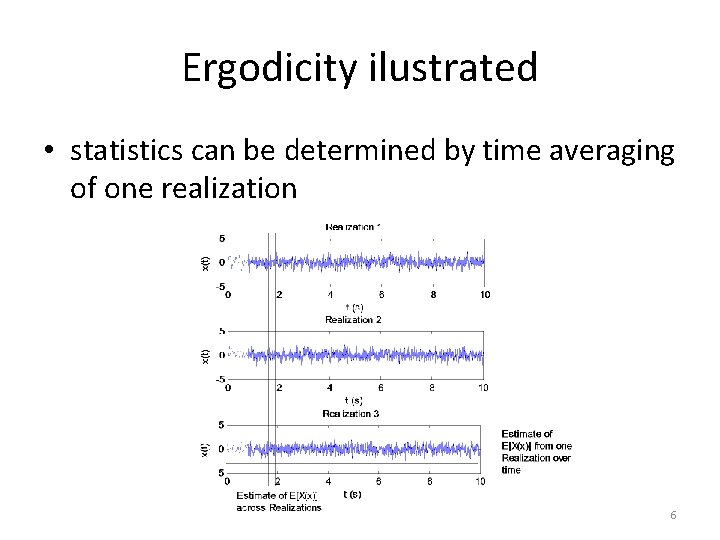
Ergodicity • A random process X(t) is ergodic if all of its statistics can be determined from a sample function of the process • That is, the ensemble averages equal the corresponding time averages with probability one. 5

Ergodicity ilustrated • statistics can be determined by time averaging of one realization 6

Ergodicity and stationarity • Wide-sense stationary: Mean and Autocorrelation is constant over time • Strictly stationary: All statistics is constant over time 7

Weak forms of ergodicity • The complete statistics is often difficult to estimate so we are often only interested in: – Ergodicity in the Mean – Ergodicity in the Autocorrelation 8

Ergodicity in the Mean • A random process is ergodic in mean if E(X(t)) equals the time average of sample function (Realization) • Where the <> denotes time averaging • Necessary and sufficient condition: X(t+τ) and X(t) must become independent as τ approaches ∞ 9

Example • 10

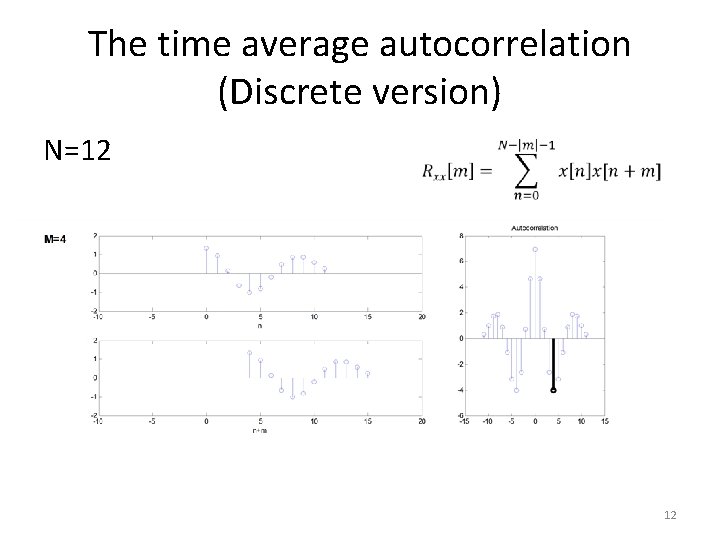
Ergodicity in the Autocorrelation • Ergodic in the autocorrelation mean that the autocorrelation can be found by time averaging a single realization • Where • Necessary and sufficient condition: X(t+τ) X(t) and X(t+τ+a) X(t+a) must become independent as a approaches ∞ 11

The time average autocorrelation (Discrete version) N=12 12

Example (1/2) Autocorrelation • A random process – where A and fc are constants, and Θ is a random variable uniformly distributed over the interval [0, 2π] – The Autocorraltion of of X(t) is: – What is the autocorrelation of a sample function? 13

Example (2/2) • The time averaged autocorrelation of the sample function • Thereby 14

Ergodicity of the First-Order Distribution • If an process is ergodic the first-Order Distribution can be determined by inputting x(t) in a system Y(t) • And the integrating the system • Necessary and sufficient condition: X(t+τ) and X(t) must become independent as τ approaches ∞ 15

Ergodicity of Power Spectral Density • A wide-sense stationary process X(t) is ergodic in power spectral density if, for any sample function x(t), 16

Example • 17

Essential equations 18

Typical signals • 19

Essential equations Distribution and density functions First-order distribution: First-order density function: 2 end order distribution 2 end order density function 20

Essential equations Expected value 1 st order (Mean) • 21

Essential equations Auto-correlations • 22

Essential equations Cross-correlations • In the general case • In the case of WSS 23

Properties of autocorrelation and crosscorrelation • Auto-correlation: Rxx(t 1, t 1)=E[|X(t)|2] When WSS: Rxx(0)=E[|X(t)|2]=σx 2+mx 2 • Cross-correlation: – If Y(t) and X(t) is independent Rxy(t 1, t 2)=E[X(t)Y(t)]=E[X(t)]E[Y(t)] – If Y(t) and X(t) is orthogonal Rxy(t 1, t 2)=E[X(t)Y(t)]=E[X(t)]E[Y(t)]=0; 24

Essential equations PSD • Truncated Fourier transform of X(t): • Power spectrum • Or from the autocorrelation – The Fourier transform of the auto-correlation 25

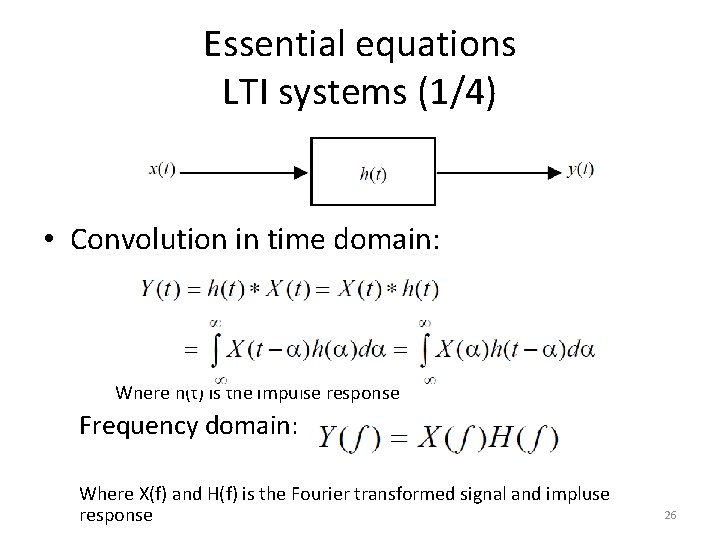
Essential equations LTI systems (1/4) • Convolution in time domain: Where h(t) is the impulse response Frequency domain: Where X(f) and H(f) is the Fourier transformed signal and impluse response 26

Essential equations LTI systems (2/4) • Expected value (mean) of the output: – If WSS: • Expected Mean square value of the output – If WSS: 27

Essential equations LTI systems (3/4) • Cross correlation function between input and output when WSS • Autocorrelation of the output when WSS 28

Essential equations LTI systems (4/4) • PSD of the output • Where H(f) is the transfer function – Calculated as the four transform of the impulse response 29

A biomedical example on a stochastic process • Analyze of Heart murmurs from Aortic valve stenosis using methods from stochastic process. 30

Introduction to heart sounds • The main sounds is S 1 and S 2 – S 1 the first heart sound • Closure of the AV valves – S 2 the second heart sound • Closure of the semilunar valves 31

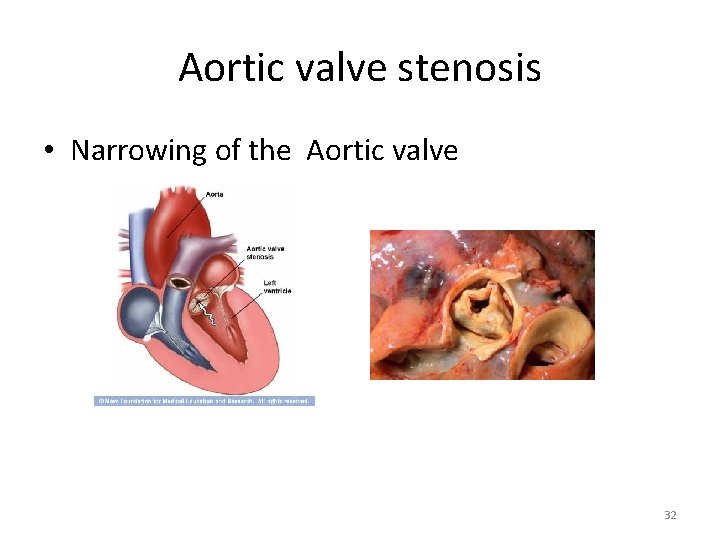
Aortic valve stenosis • Narrowing of the Aortic valve 32

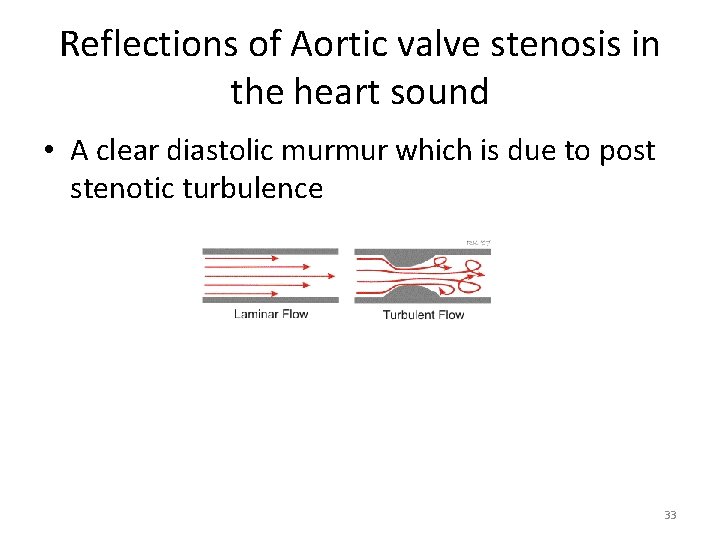
Reflections of Aortic valve stenosis in the heart sound • A clear diastolic murmur which is due to post stenotic turbulence 33

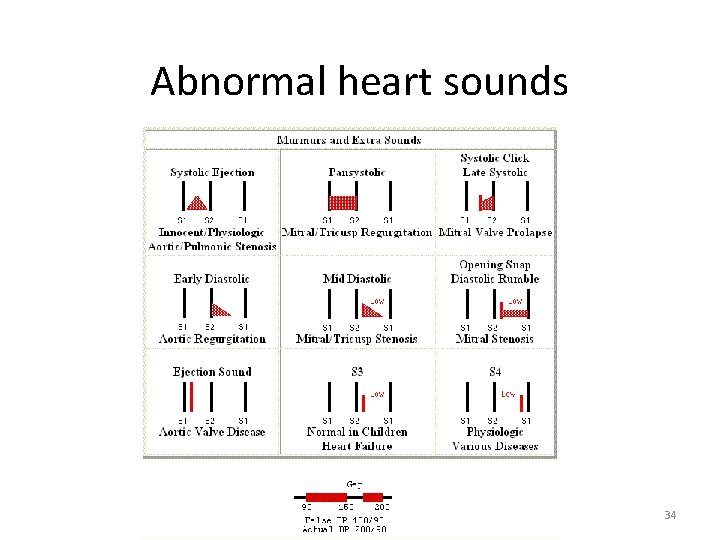
Abnormal heart sounds 34

Signals analyze for algorithm specification • Is heart sound stationary, quasi-stationary or non-stationary? • What is the frequency characteristic of systolic Murmurs versus a normal systolic period? 35

exercise • Chi meditation and autonomic nervous system 36