Stochastic models time series Random process an infinite









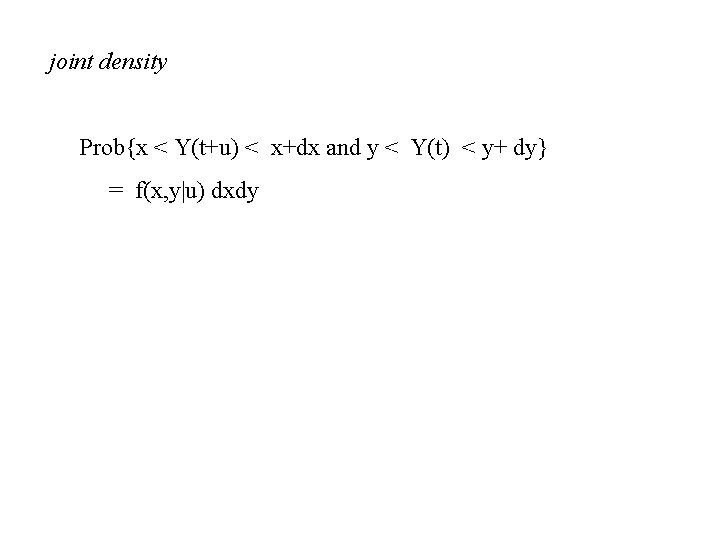


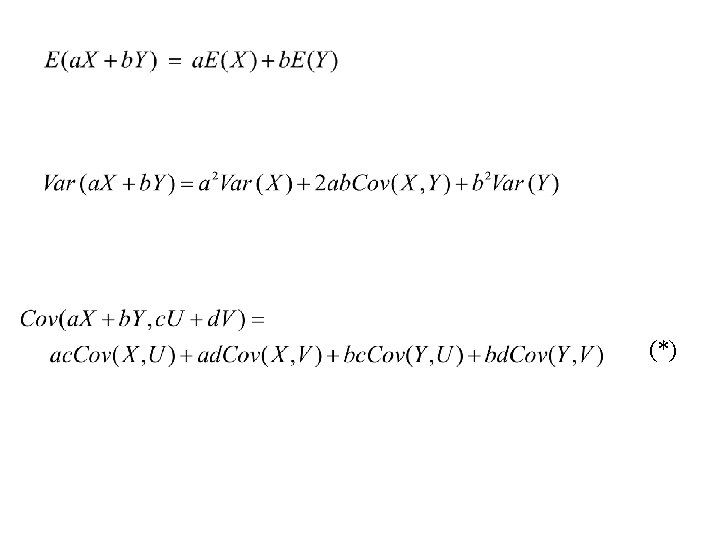






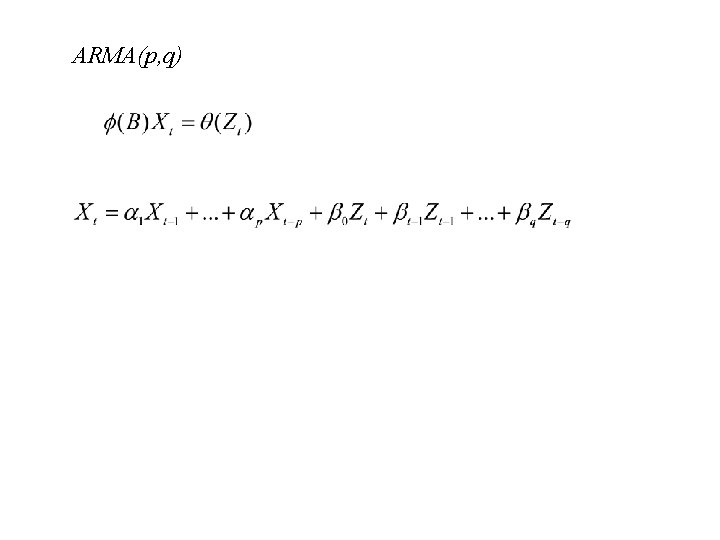



- Slides: 24

Stochastic models - time series. Random process. an infinite collection of consistent distributions probabilities exist Random function. a family of random variables, e. g. {Y(t), t in Z}

Specified if given F(y 1, . . . , yn; t 1 , . . . , tn ) = Prob{Y(t 1) y 1, . . . , Y(tn ) yn } that are symmetric F( y; t) = F(y; t), a permutation compatible F(y 1 , . . . , ym , , . . . , ; t 1, . . . , tm+1, . . . , tn} = F(y 1, . . . , ym; t 1, . . . , tm)

Finite dimensional distributions First-order F(y; t) = Prob{Y(t) t} Second-order F(y 1, y 2; t 1, t 2) = Prob{Y(t 1) y 1 and Y(t 2) y 2} and so on

Other methods i) Y(t; ), : random variable ii) urn model iii) probability on function space iv) analytic formula Y(t) = cos( t + ) : fixed : uniform on (- , ]

There may be densities The Y(t) may be discrete, angles, proportions, . . . Kolmogorov extension theorem. To specify a stochastic process give the distribution of any finite subset {Y( 1), . . . , Y( n)} in a consistent way, in A

Moment functions. Mean function c. Y(t) = E{Y(t)} = y d. F(y; t) = y f(y; t) dy if continuous = yjf(yj; t) if discrete E{ 1 Y 1(t) + 2 Y 2(t)} = 1 c 1(t) + 2 c 2(t) vector-valued case mean level - signal plus noise: S(t) + (t) S(. ): fixed

Second-moments. autocovariance function c. YY(s, t) = cov{Y(s), Y(t)} = E{Y(s)Y(t)} - E{Y(s)}E{Y(t)} non-negative definite j kc. YY(tj , tk ) 0 crosscovariance function c 12(s, t) = cov{Y 1(s), Y 2(t)} scalars

Stationarity. Joint distributions, {Y(t+u 1), . . . , Y(t+uk-1), Y(t)}, do not depend on t for k=1, 2, . . . Often reasonable in practice - for some time stretches Replaces "identically distributed"

mean E{Y(t)} = c. Y for t in Z autocovariance function cov{Y(t+u), Y(t)} = c. YY(u) t, u in Z u: lag = E{Y(t+u)Y(t)} if mean 0 autocorrelation function (u) = corr{Y(t+u), Y(t)}, | (u)| 1 crosscovariance function cov{X(t+u), Y(t)} = c. XY(u)
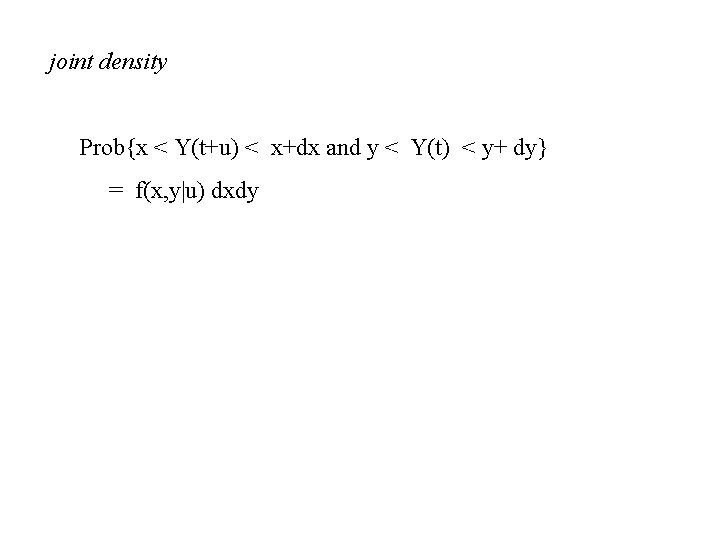
joint density Prob{x < Y(t+u) < x+dx and y < Y(t) < y+ dy} = f(x, y|u) dxdy

Some useful models Chatfield notation Purely random / white noise often mean 0 Building block

Random walk not stationary
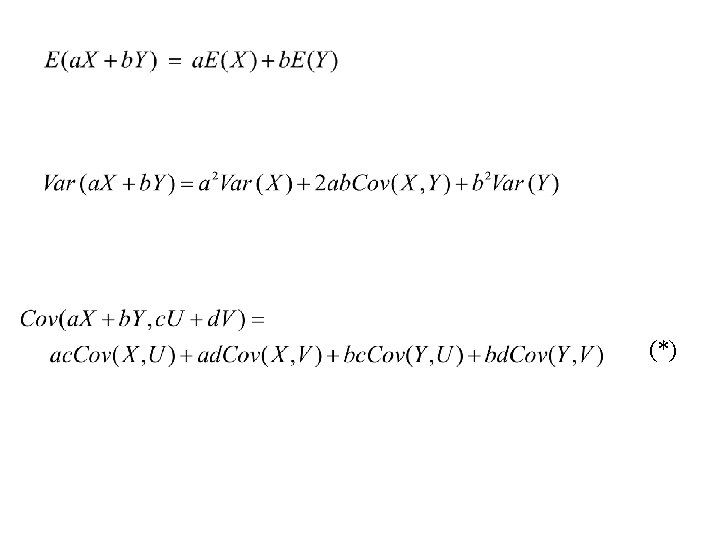

Moving average, MA(q) From (*) stationary

MA(1) 0=1 1 = -. 7

Backward shift operator Linear process. Need convergence condition

autoregressive process, AR(p) first-order, AR(1) Markov * Linear process For convergence/stationarity

a. c. f. From (*) p. a. c. f. corr{Y(t), Y(t-m)|Y(t-1), . . . , Y(t-m+1)} = 0 for m p when Y is AR(p) linearly

In general case, Useful for prediction
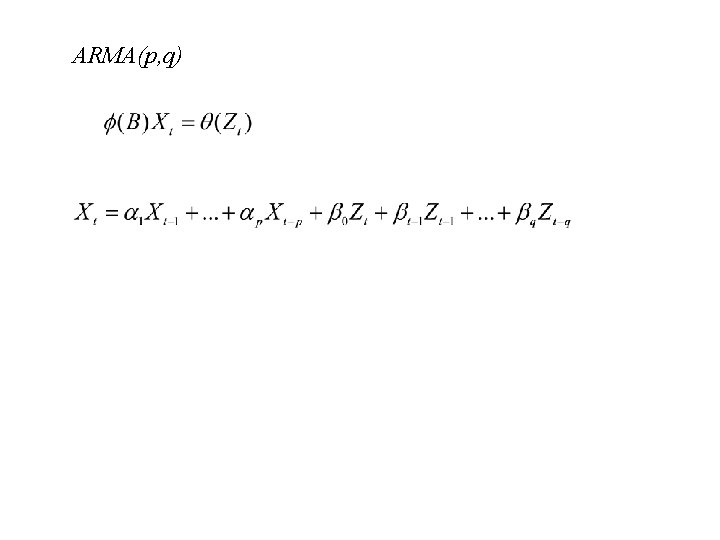
ARMA(p, q)

ARIMA(p, d, q).

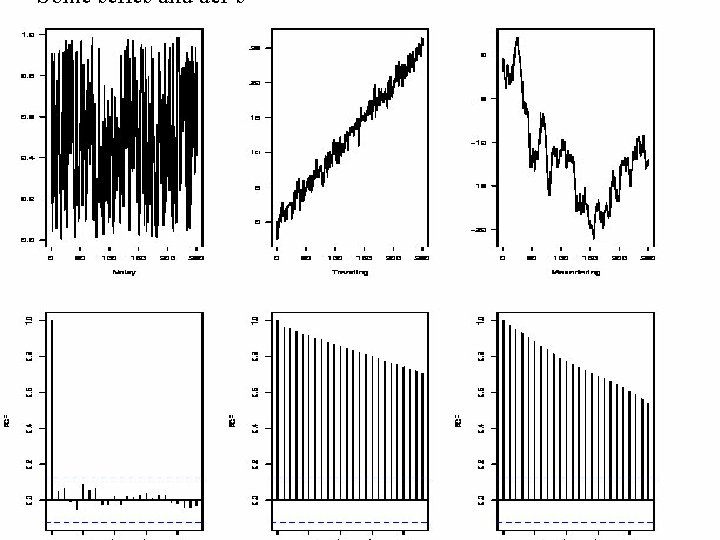
Some series and acf’s

Yule-Walker equations for AR(p). Correlate, with Xt-k , each side of

Cumulants. multilinear functional 0 if some subset of variantes independent of rest 0 of order > 2 for normal is determined by its moments