Stochastic Modeling in Systems Biology and Biophysics Subhadip

Stochastic Modeling in Systems Biology and Biophysics Subhadip Raychaudhuri Indraprastha Institute of Information Technology Delhi (IIITD) Fundamentals of Systems Biology University of Delhi Dec 24 (2014)

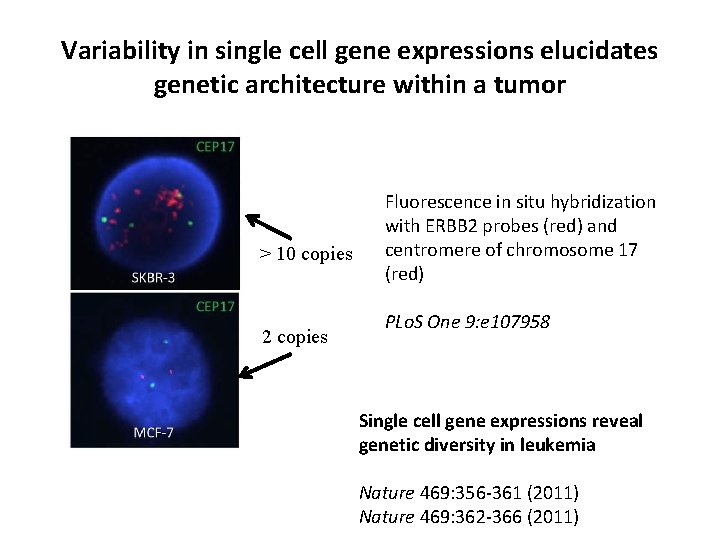
Variability in single cell gene expressions elucidates genetic architecture within a tumor > 10 copies 2 copies Fluorescence in situ hybridization with ERBB 2 probes (red) and centromere of chromosome 17 (red) PLo. S One 9: e 107958 Single cell gene expressions reveal genetic diversity in leukemia Nature 469: 356 -361 (2011) Nature 469: 362 -366 (2011)

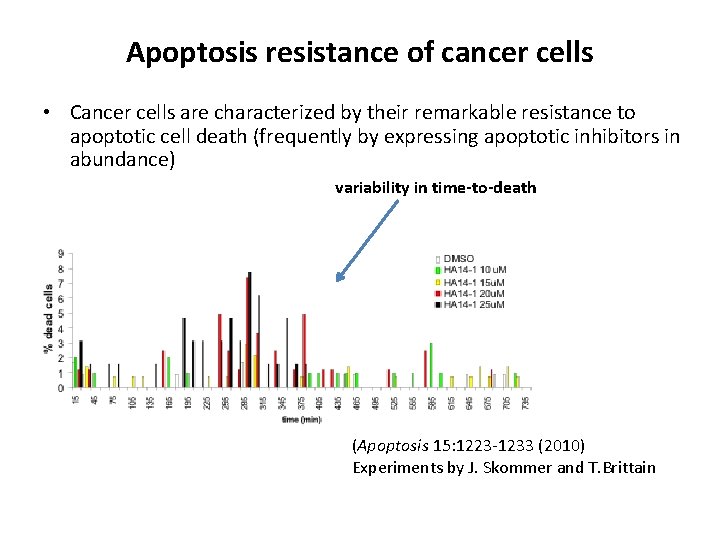
Apoptosis resistance of cancer cells • Cancer cells are characterized by their remarkable resistance to apoptotic cell death (frequently by expressing apoptotic inhibitors in abundance) variability in time-to-death (Apoptosis 15: 1223 -1233 (2010) Experiments by J. Skommer and T. Brittain

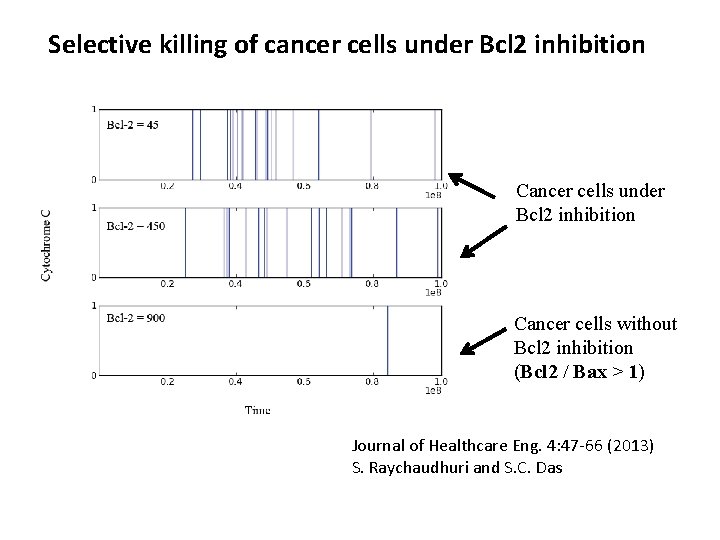
Selective killing of cancer cells under Bcl 2 inhibition Cancer cells without Bcl 2 inhibition (Bcl 2 / Bax > 1) Journal of Healthcare Eng. 4: 47 -66 (2013) S. Raychaudhuri and S. C. Das

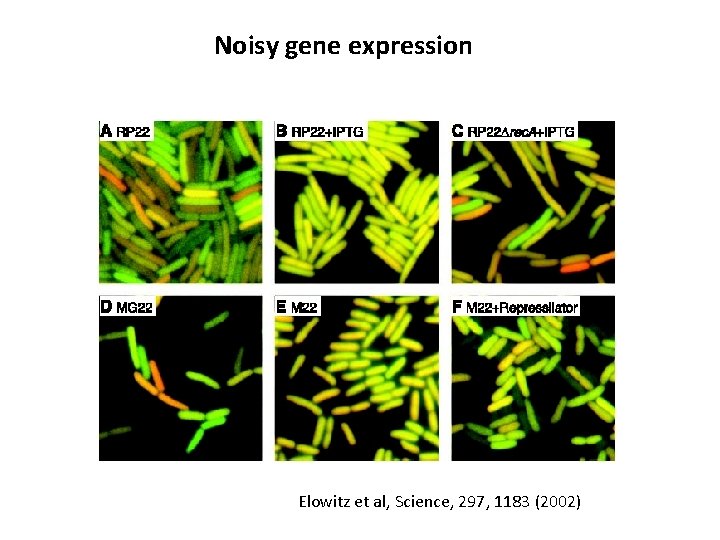
Noisy gene expression Elowitz et al, Science, 297, 1183 (2002)

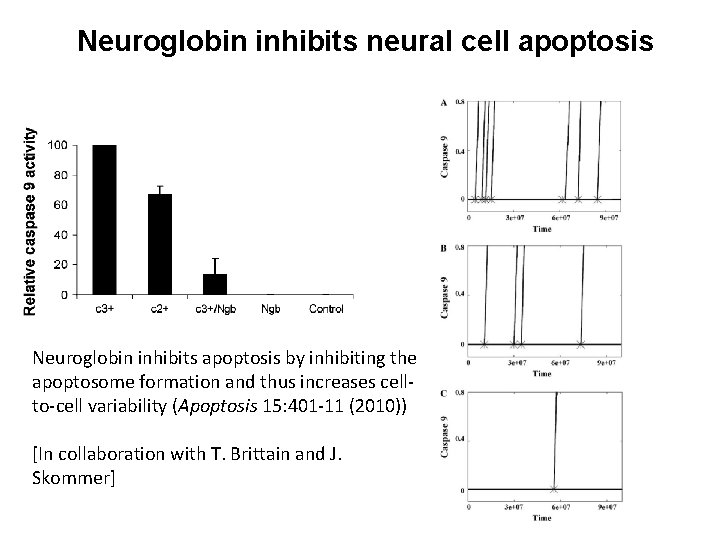
Neuroglobin inhibits neural cell apoptosis Neuroglobin inhibits apoptosis by inhibiting the apoptosome formation and thus increases cellto-cell variability (Apoptosis 15: 401 -11 (2010)) [In collaboration with T. Brittain and J. Skommer]

What is common in all these? ØCell-to-cell stochastic variability (stochastic fluctuation)

Stochastic fluctuations / Stochastic variability / Noise Some more examples ……. .

Analysis of single cell gene expressions can provide insight into cancer and degenerative disorders Ø Single cell gene expressions provide insight into genetic diversity in a tumor cell population Ø Single cell study seems to be important in elucidating cancer stem cells and apoptosis resistance Ø Single cell gene expressions could elucidate molecular pathogenesis of various neurological diseases Nature 469: 356 -361 (2011) Nature 469: 362 -366 (2011) Neuro. Rx: 3: 302 -318 (2006)

Selective killing of cancer cells by targeting the apoptotic pathway Ø Variability in cell-to-cell stochastic fluctuation in apoptotic activation between cancer and healthy cells can be utilized in selective targeting Ø In certain cancers, a stochastic to deterministic transition in apoptotic activation might be possible to achieve (such as type 2 type 1 transition) Ø Healthy cells should mostly remain protected by large cell-to-cell variability in apoptotic activation

Increasing cell-to-cell variability in apoptosis can be a strategy to treat degenerative disorders Ø Caspase 6 inhibition may lead to type 1 type 2 transition in a large number of neural cells that are undergoing degeneration Ø Increasing the Bcl 2/Bax ratio (to > 1) or lowering the probability of apoptosome formation can also be effective in certain cases Systems and Synthetic Biology 8: 83 -97 (2014) PLo. S One 5: e 13437 (2010)

Neural cell apoptosis: implications for developmental biology and neurodegenerative diseases • Mechanisms for proper development of neural synaptic connections remain a key question in developmental biology • There seems to be massive neuronal cell death both during development and in neural degeneration (trauma, stroke, neurodegenerative disorders) Ø Our model is based on cytochrome c reaction with Apaf (pro-apoptotic) and neuroglobin (anti-apoptotic) (may hold the key to understanding how proper synaptic connections are made between neurons) http: //andreeasanatomy. blogspot. in/2011/04/

Mechanisms for single cell origin of cancer Ø Cancer cells seem to originate from a single cell (one single cell out of many healthy cells start clonal expansion of a tumor) Biology of Cancer, by Weinberg Ø Mutation in a single oncogene (such as Bcl 2) may lead to increased cell-to-cell variability (resulting in slow activation) in apoptotic activation

Mechanisms for single cell origin of neural stem cells Ø Neural stem cells seem to originate from a single cell (one single cell out of several similar cells) Ø A simple feed-back activation based model of Notch-Delta signaling can provide insight into single cell mechanisms for origin of neural stem cells Principles of Development Wolpert & Tickle

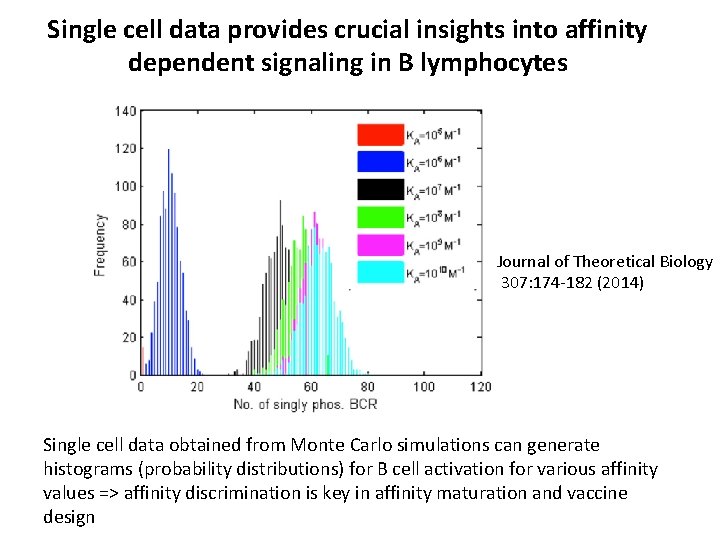
Single cell data provides crucial insights into affinity dependent signaling in B lymphocytes Journal of Theoretical Biology 307: 174 -182 (2014) Single cell data obtained from Monte Carlo simulations can generate histograms (probability distributions) for B cell activation for various affinity values => affinity discrimination is key in affinity maturation and vaccine design

Modeling of stochastic processes: some historical examples Ø Random walk motion known as Brownian motion (diffusion equation approach by Einstein and stochastic equation of Langevin) Ø Fluctuations in stock markets (diffusion equation and stochastic equation) Ø Fluctuations in birth-death processes (such as in population biology)(modeled using Master equations) Ø Noise in electronic systems (Master equations) Stochastic Methods by C. Gardiner

Theoretical basis of stochastic / probabilistic approaches Stochastic processes describe systems that evolve in time in a probabilistic manner Example: outcome of tossing a coin HTTTTHHHHHTT Markov processes: Outcome of a particular time-step depends solely on the state of the system in the preceding step Example: random walk motion of a particle

Chapman-Kolmogorov formalism Markov property implies: P(x 2, t 2; x 1, t 1| x 0, t 0) = P(x 2, t 2|x 1, t 1) P(x 1, t 1|x 0, t 0) The conditional probability density satisfies P(x 2, t 2|x 0, t 0) = dx 1 P(x 2, t 2|x 1, t 1) P(x 1, t 1|x 0, t 0) P(xi, ti|xj, tj) probability density for a particle being at xi at time ti given that it was at xj at time tj

Master equation formalism Pi(t) probability that the system is in state i at time t Wij(t) transition probability from state j i Master equation for a simple random walk

Master equation formalism Master equation for a simple random walk Continuum limit of the RW Master equation Known as Fokker-Planck equation (obtained by Taylor expanding P(x l, t)) Can be obtained as (i) Differential form of Chapman-Kolmogorov equation (ii) From the corresponding stochastic equation (Langevin equation)

In Silico approach • Monte Carlo (stochastic) simulations Ø solving master equations on a computer Ø stochastic simulations can capture dynamics of biological processes • Stochastic equations may also provide insight into certain cases (such as in the underlying design principles of a robust functional response)

Stochastic simulation approach • Gillespie’s stochastic simulation algorithm (SSA) • Kinetic Monte Carlo simulations Ø Both involve solving master equations on a computer (in silico)

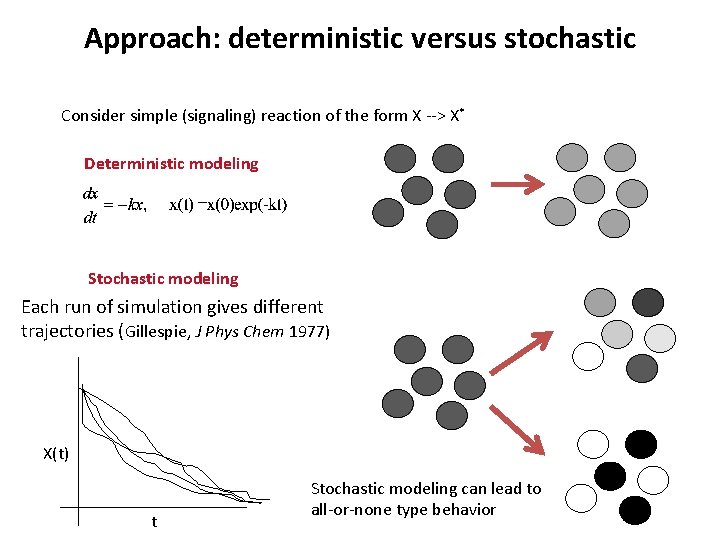
Approach: deterministic versus stochastic Consider simple (signaling) reaction of the form X --> X* Deterministic modeling Stochastic modeling Each run of simulation gives different trajectories (Gillespie, J Phys Chem 1977) X(t) t Stochastic modeling can lead to all-or-none type behavior

Approach: deterministic versus stochastic Consider simple (signaling) reaction of the form X --> X* Deterministic modeling Above ODE is obtained in the following manner: When x(t) or k is very small ODE limit is no longer valid => Instead, kxΔt can be considered as the probability of reaction

Gillespie’s Stochastic simulation approach Start with Master equation that describes the time-evolution equation for the function P(X 1, X 2, …XN, t) P(X 1, X 2, …XN, t+dt) = P(X 1, X 2, …XN; t)[1 - aμ dt] + Bμ dt => / t P(X 1, X 2, …XN, t) = [ Bμ - aμ P(X 1, X 2, …XN, t) ] Probability that the next reaction will occur after time τ P 0(τ) = exp (- aν τ) Probability that the next reaction will be the μth reaction μ-1 μ P(μ) = aν < r a 0 ≤ aν M a 0 = a ν

Kinetic Monte Carlo simulation approach Start with Master equation that describes the timeevolution equation for the function P(X 1, X 2, …XN, t) P(X 1, X 2, …XN, t+dt) = P(X 1, X 2, …XN; t)[1 - aμ dt] + Bμ dt => / t P(X 1, X 2, …XN, t) = [ Bμ - aμ P(X 1, X 2, …XN, t) ] Define a set of probability constants aμ Δt (from state X 1, X 2, …XN, t) At each Monte Carlo step carry out moves with r < aμ Δt

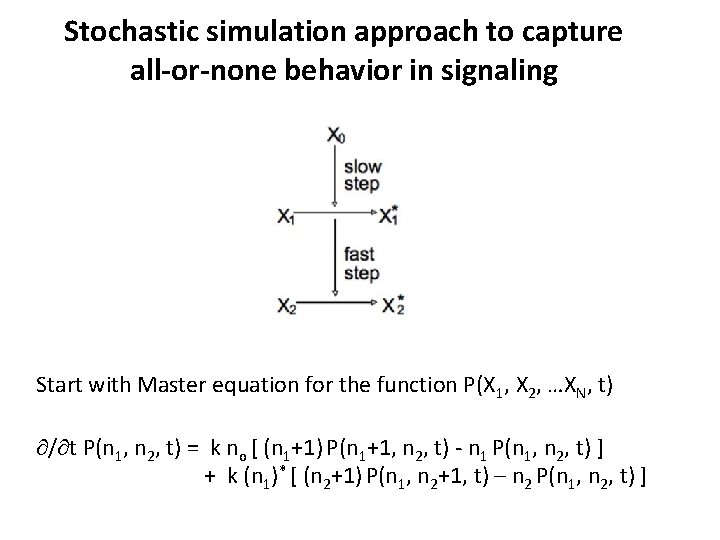
Stochastic simulation approach to capture all-or-none behavior in signaling Start with Master equation for the function P(X 1, X 2, …XN, t) / t P(n 1, n 2, t) = k no [ (n 1+1) P(n 1+1, n 2, t) - n 1 P(n 1, n 2, t) ] + k (n 1)* [ (n 2+1) P(n 1, n 2+1, t) – n 2 P(n 1, n 2, t) ]

Stochastic simulation approach to capture all-or-none behavior in signaling Gillespie’s SSA: Probability that the next reaction will occur after time τ P 0(τ) = exp (- aν τ) = exp(- a 0 τ) => τ = (1/a 0) log(1/r) Probability that the next reaction will be the μth reaction P 0(1) = 0 < r a 0 ≤ k 1 n 0 n 1 & P 0(2) = k 1 n 0 n 1 < r a 0 ≤ a 0 = k 1 n 0 n 1 + k 2 (n 1)* n 2 Kinetic Monte Carlo: P(n 1, n 2, t+Δt) - P(n 1, n 2, t+Δt) = (k 1 no Δt) [ (n 1+1) P(n 1+1, n 2, t) - n 1 P(n 1, n 2, t) ] P(n 1, n 2, t+Δt) - P(n 1, n 2, t+Δt) = (k 2 (n 1)* Δt) [ (n 2+1) P(n 1, n 2+1, t) – n 2 P(n 1, n 2, t) ] Carry out n 1 – 1 with prob = k 1 no n 1 Δt Carry out n 2 – 1 with prob = k 2 (n 1)* n 2 Δt

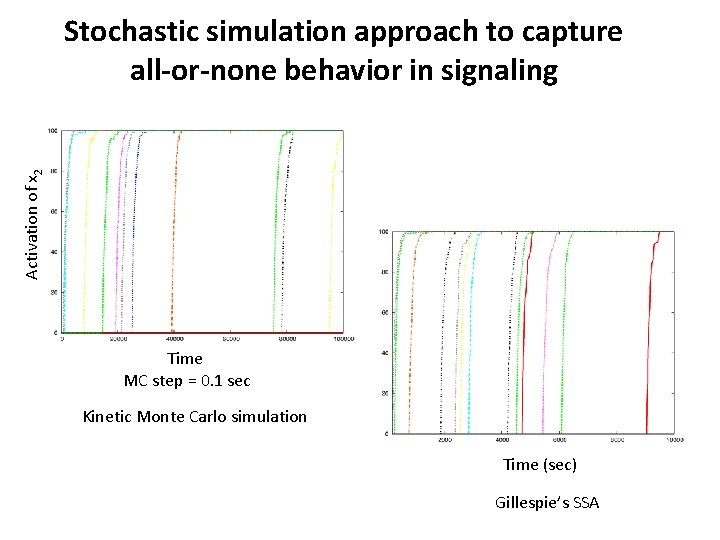
Activation of x 2 Stochastic simulation approach to capture all-or-none behavior in signaling Time MC step = 0. 1 sec Kinetic Monte Carlo simulation Time (sec) Gillespie’s SSA

Implementation of kinetic Monte Carlo (MC) § Simulation is carried out on a cubic lattice § Only one molecule per node § Signaling molecules can diffuse in 2 D (surface bound) or in 3 D (intracellular) with specified probability of diffusion Pdiff § Signaling molecules undergo reactions with specified probabilities Pon, Poff, Pcat. Schematics of the 3 D simulation lattice Lattice picture: http: //www. mikeblaber. org/oldwine/chm 1045/not es/Forces/Solids/lattice. gif One simulation run (single cell) takes between ~ minutes to ~ days (using a reduced system size for computationally intensive simulations)

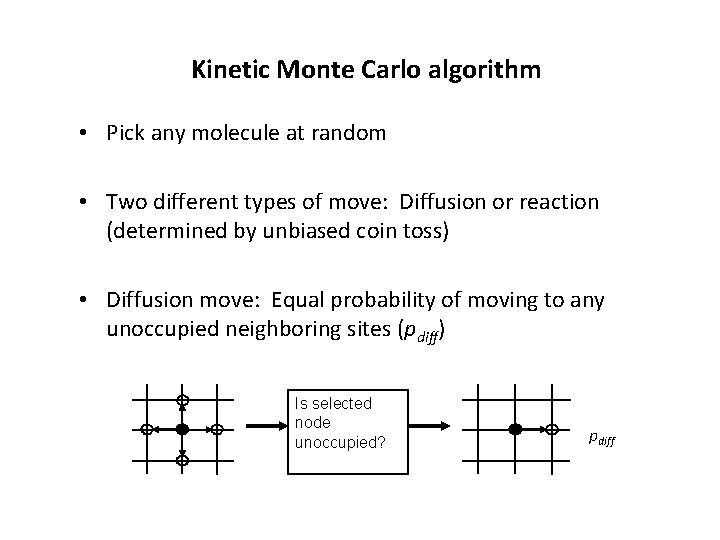
Kinetic Monte Carlo algorithm • Pick any molecule at random • Two different types of move: Diffusion or reaction (determined by unbiased coin toss) • Diffusion move: Equal probability of moving to any unoccupied neighboring sites (pdiff) Is selected node unoccupied? pdiff

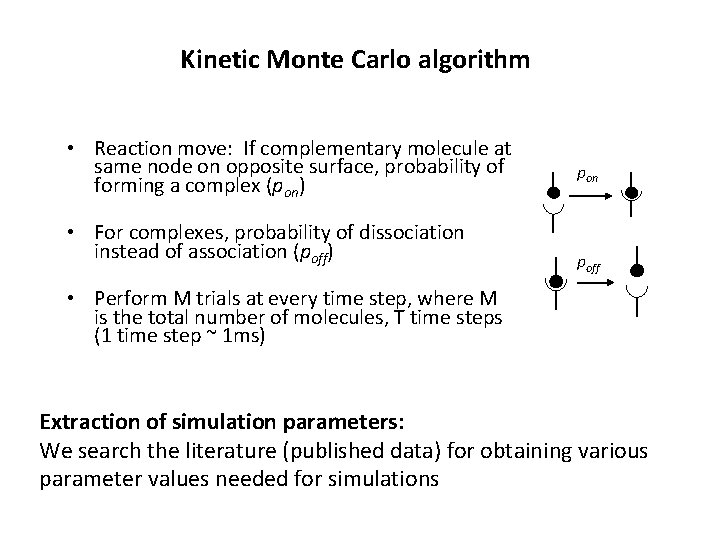
Kinetic Monte Carlo algorithm • Reaction move: If complementary molecule at same node on opposite surface, probability of forming a complex (pon) • For complexes, probability of dissociation instead of association (poff) pon poff • Perform M trials at every time step, where M is the total number of molecules, T time steps (1 time step ~ 1 ms) Extraction of simulation parameters: We search the literature (published data) for obtaining various parameter values needed for simulations

Kinetic Monte Carlo algorithm Ø Suitable for simulating biological processes at the molecular, cellular and tissue level Ø Current simulations involve length scales ~ 1 nm – micro-meters and time-scales ~ minutes – hours Ø It can capture stochastic fluctuations (such as cell-to-cell variability) Ø It can simulate biological complexity such as spatial heterogeneity or complicated signaling regulations

Hybrid approaches in kinetic Monte Carlo Ø Suitable for simulating very complex biological processes (Often such simulations span multiple length and time scales) Hybrid simulation to capture the dynamics of receptor-lipid raft formation involve systems level approach combining: • Diffusion of membrane molecules (receptors and lipids) based on energetics (thermodynamic free energy and detail balance) • Probabilistic rate constant based kinetic MC for membrane proximal and intracellular signaling • Membrane shape fluctuations (governed by membrane mechanical properties surface tension and bending rigidity that will depend on lipid composition of the membrane)

Modeling of stochastic variability in biology: type 1/type 2 choice in apoptotic cell death and selective killing of cancer cells Single cell approach is essential in elucidating Ø the type 1/ type 2 choice in apoptotic cell death (a key problem in the biology of apoptosis) Ø the mechanisms for selective killing of cancer cells (that would protect healthy cells)

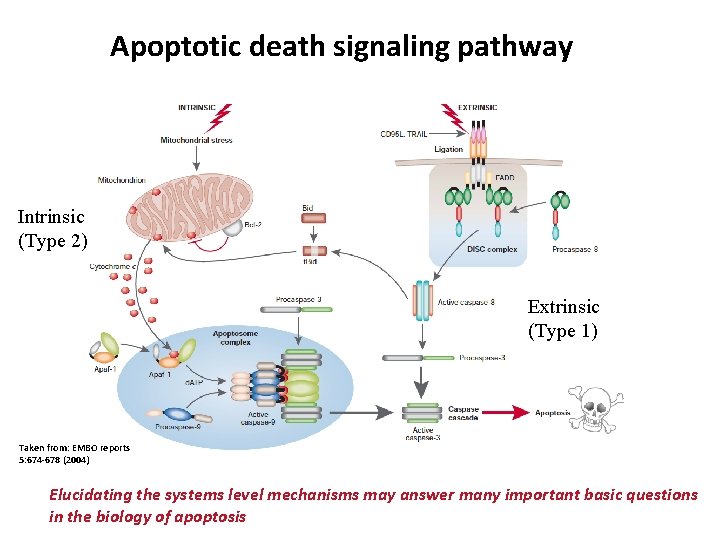
Apoptotic death signaling pathway Intrinsic (Type 2) Extrinsic (Type 1) Taken from: EMBO reports 5: 674 -678 (2004) Elucidating the systems level mechanisms may answer many important basic questions in the biology of apoptosis

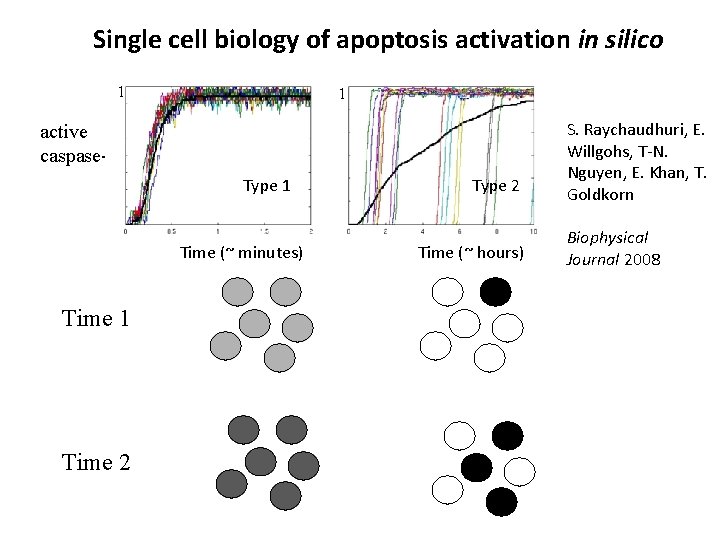
Single cell biology of apoptosis activation in silico 1 1 active caspase-3 Type 1 Time (~ minutes) Time 1 Time 2 Type 2 Time (~ hours) S. Raychaudhuri, E. Willgohs, T-N. Nguyen, E. Khan, T. Goldkorn Biophysical Journal 2008

Single cell biology of apoptosis activation in silico Each run of Monte Carlo corresponds to activation at the level of single cells (but we need many runs) We need many cores / processors • Monte Carlo simulation emerges as a powerful tool to study single cell biology of apoptosis (or other biological processes) Combining pre-generation of a random numbers with recycling (on parallel processors) may accelerate the simulation runs => pre-generated sequence of accept/reject moves

Data analysis for single cell biology of apoptosis activation • Monte Carlo simulation emerge as a powerful tool to study single cell biology of apoptosis (or other biological processes) • New challenges involved in data analysis (such as estimating time-to-death) • Probability distribution based approaches turn out to be insightful

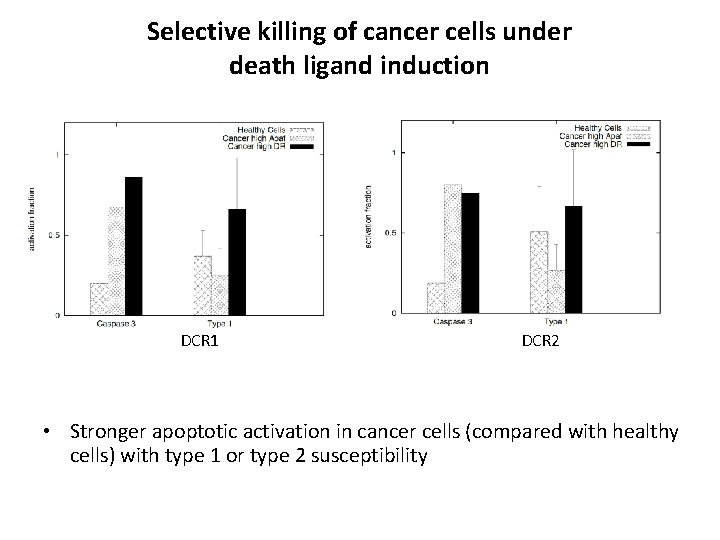
Selective killing of cancer cells under death ligand induction DCR 1 DCR 2 • Stronger apoptotic activation in cancer cells (compared with healthy cells) with type 1 or type 2 susceptibility

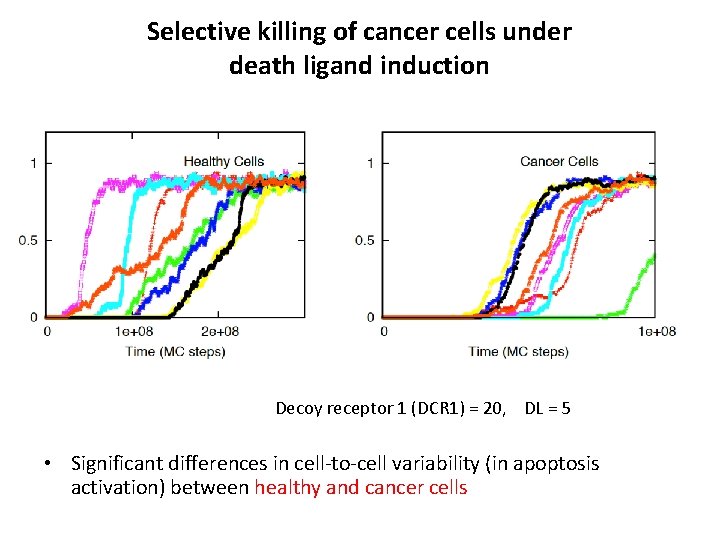
Selective killing of cancer cells under death ligand induction Decoy receptor 1 (DCR 1) = 20, DL = 5 • Significant differences in cell-to-cell variability (in apoptosis activation) between healthy and cancer cells

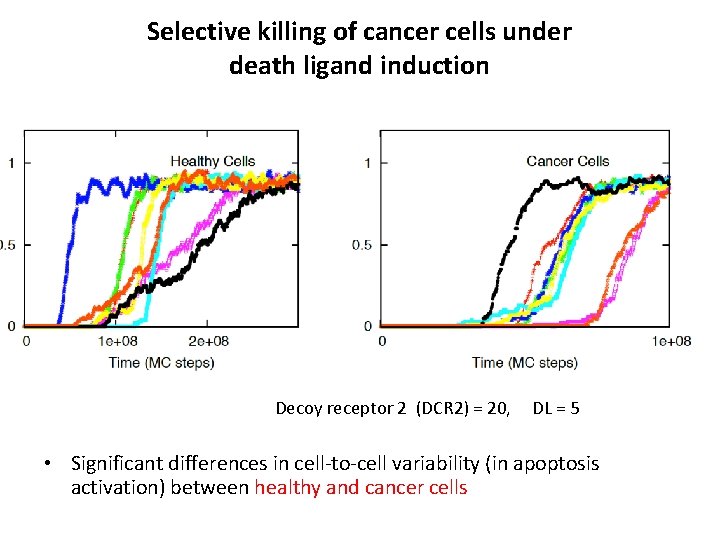
Selective killing of cancer cells under death ligand induction Decoy receptor 2 (DCR 2) = 20, DL = 5 • Significant differences in cell-to-cell variability (in apoptosis activation) between healthy and cancer cells

Cell-to-cell variability in biological Processes Cell-to-cell variability in biological dynamics may arise due to • Inherent cell-to-cell differences in the genomic and proteomic state • Inherent fluctuations in signaling reactions (arise when low number of molecules are present, low number of molecules emerge due to inhibition or low probability of reaction is involved) • Often these two effects are synergistic leading to large cell-to-cell stochastic variability in response (may result in distinct functional outcomes and signaling phenotypes)