Stochastic Image Denoising using Minimum Mean Squared Error

Stochastic Image Denoising using Minimum Mean Squared Error (Wiener) Filtering 1 ECEN 670 MINI-CONFERENCE PROJECT BRANDON CARROLL LAITH SAHAWNEH ECEN 670 CLASS STOCHASTIC PROCESSES BYU-ECE Department 2/6/2022

Outline 2 �Introduction �Theory: Wiener Filter Derivation �Results & Analysis �Conclusion BYU-ECE Department 2/6/2022

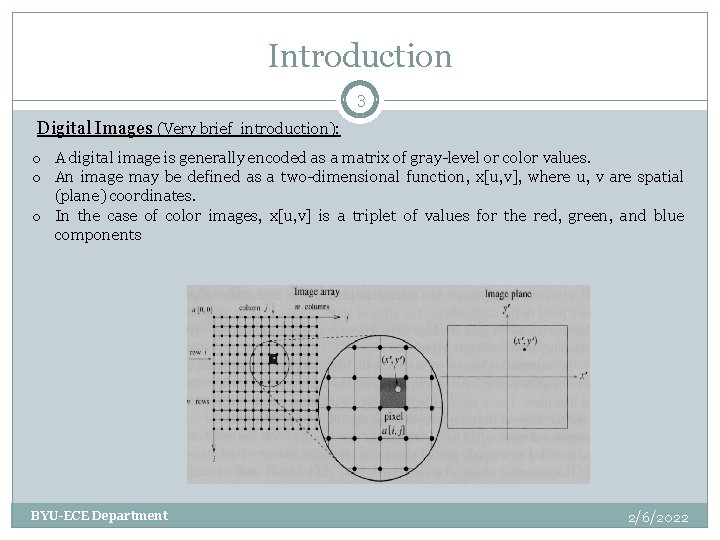
Introduction 3 Digital Images (Very brief introduction): o A digital image is generally encoded as a matrix of gray-level or color values. o An image may be defined as a two-dimensional function, x[u, v], where u, v are spatial (plane) coordinates. o In the case of color images, x[u, v] is a triplet of values for the red, green, and blue components BYU-ECE Department 2/6/2022

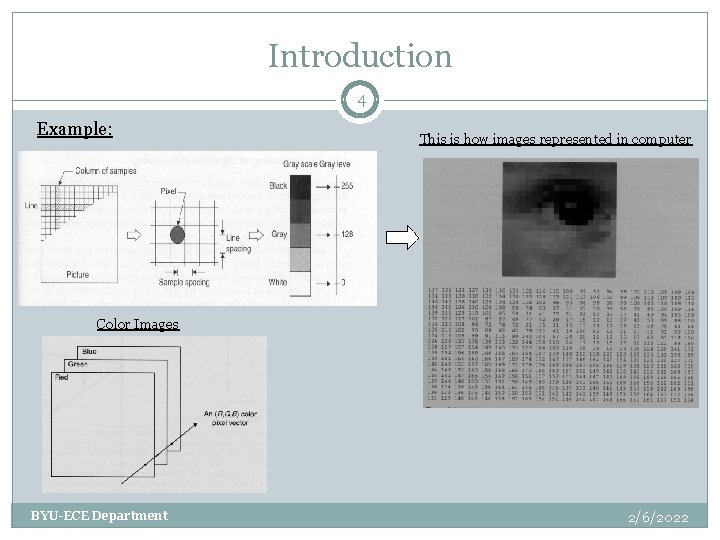
Introduction 4 Example: This is how images represented in computer Color Images BYU-ECE Department 2/6/2022

Introduction 5 Image Denoising and Restoration: 1. Image denoising is one of the fundamental challenges in the field of image processing. 2. Employed using variety of configurations in a wide variety of applications: namely: Object recognition, photo enhancement, and image restoration. 3. The objective of image restoration is to improve a given image in some predefined sense. Image restoration attempts to reconstruct or recover a degraded image by using a priori knowledge of the degradation phenomenon. BYU-ECE Department 2/6/2022

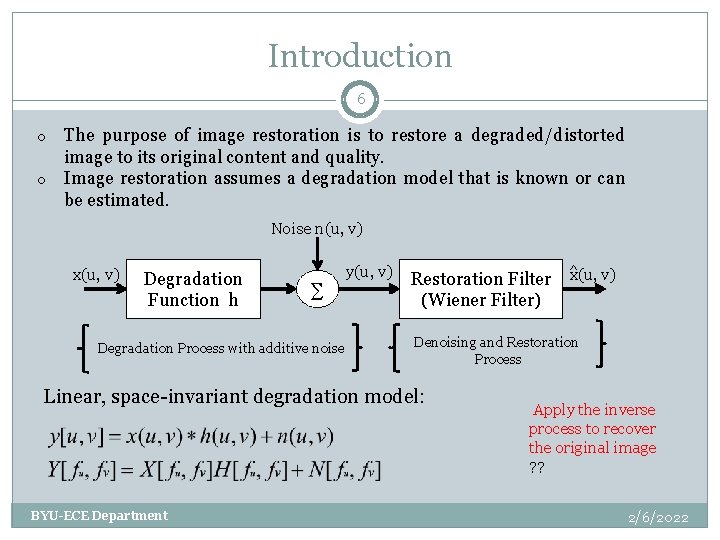
Introduction 6 The purpose of image restoration is to restore a degraded/distorted image to its original content and quality. o Image restoration assumes a degradation model that is known or can be estimated. o Noise n(u, v) x(u, v) Degradation Function h ∑ Degradation Process with additive noise y(u, v) Restoration Filter (Wiener Filter) Denoising and Restoration Process Linear, space-invariant degradation model: BYU-ECE Department x(u, v) Apply the inverse process to recover the original image ? ? 2/6/2022

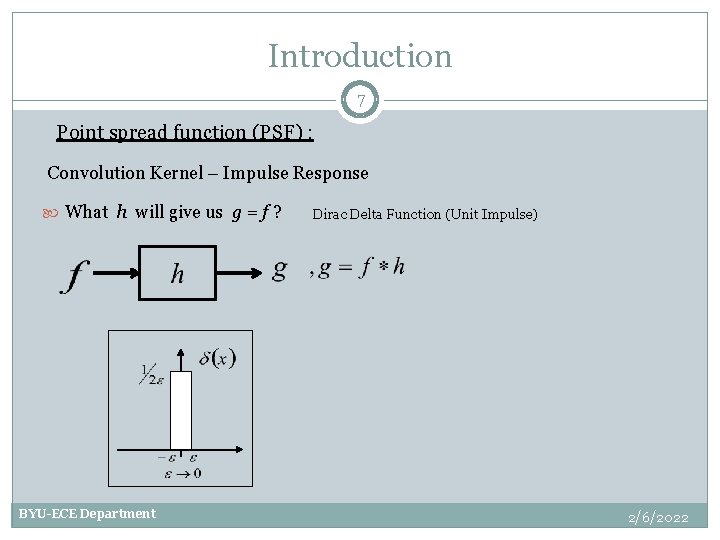
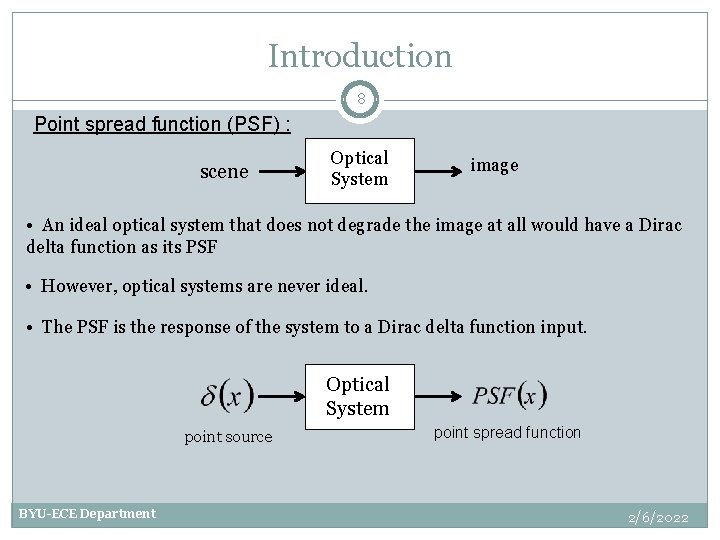
Introduction 7 Point spread function (PSF) : Convolution Kernel – Impulse Response What h will give us g = f ? BYU-ECE Department Dirac Delta Function (Unit Impulse) 2/6/2022

Introduction 8 Point spread function (PSF) : scene Optical System image • An ideal optical system that does not degrade the image at all would have a Dirac delta function as its PSF • However, optical systems are never ideal. • The PSF is the response of the system to a Dirac delta function input. Optical System point source BYU-ECE Department point spread function 2/6/2022

Introduction 9 Point spread function (PSF) : The impulse is a point (or pixel) of light The impulse response is commonly referred to as the PSF Impulse of Light BYU-ECE Department Image (degraded) impulse 2/6/2022

Introduction 10 Noise models o o o Most types of noise are modeled as probability density functions (PDFs) Noise model is decided based on understanding of the physics of the sources of noise. Ø Gaussian: poor illumination Ø Rayleigh: range image Ø Gamma, exp: laser imaging Ø Impulse: faulty switch during imaging, Ø Uniform: quantization. Parameters can be estimated based on histogram on small flat area of an image. De-noising o o Spatial filtering (Mean filters, Median, Max, Min …) Frequency domain filtering ( Inverse Filter, Wiener Filter, …) BYU-ECE Department 2/6/2022

Introduction 11 Estimation of noise parameters: 1. Gaussian Noise 2. Uniform Noise 3. Impulse (Salt& Pepper) Noise BYU-ECE Department 2/6/2022

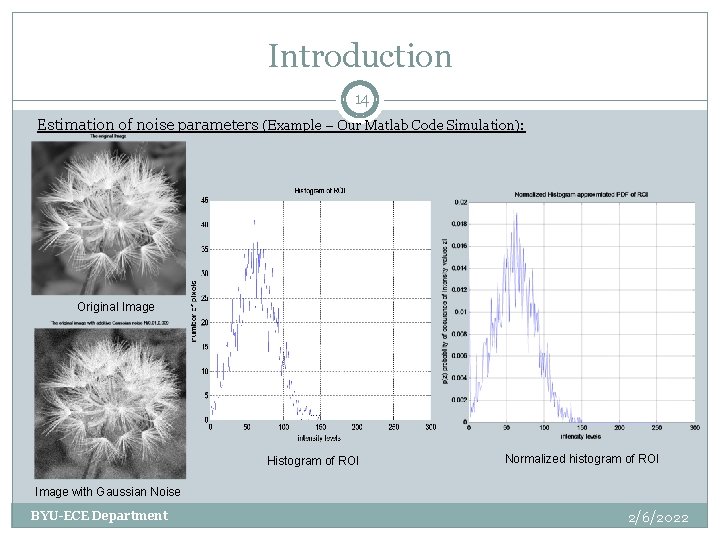
Introduction 12 Estimation of noise parameters: o The parameters of noise in the spatial domain may be known from the sensors specification or a priori-knowledge of noise distribution. o In most cases it is necessary to estimate these parameters to specify the corresponding noise PDF from sample images being denoised. How to estimate the noise parameters? 1. The common approach is to select a region of interest (ROI) in an image with as featureless a background as possible, so that the variability of intensity values in the region will be due primarily to noise! { Let zi be a discrete random variable that denotes intensity levels in an image, and p(zi), i = 1, 2, . . . , L - 1 be the corresponding normalized histogram, where, L is the number of possible intensity values. The histogram component p(zi) is an estimate of the probability of occurrence of intensity value zi. } BYU-ECE Department 2/6/2022

Introduction 13 Estimation of noise parameters: 2. Find the histogram of ROI. 3. Normalized histogram of (ROI) which can be viewed as an approximation of the intensity PDF! 4. Describe the shape of noise PDF via its central moments (estimate the mean and variance and then compute a and b variables if needed). BYU-ECE Department 2/6/2022

Introduction 14 Estimation of noise parameters (Example – Our Matlab Code Simulation): Original Image Histogram of ROI Normalized histogram of ROI Image with Gaussian Noise BYU-ECE Department 2/6/2022

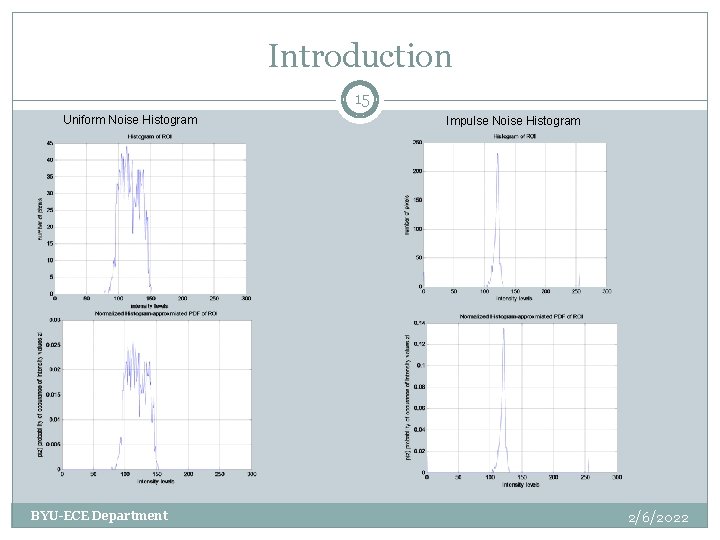
Introduction 15 Uniform Noise Histogram BYU-ECE Department Impulse Noise Histogram 2/6/2022

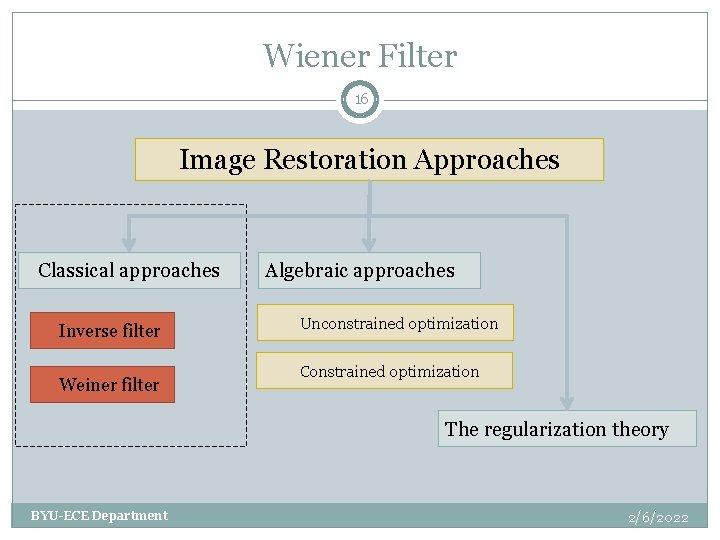
Wiener Filter 16 Image Restoration Approaches Classical approaches Inverse filter Weiner filter Algebraic approaches Unconstrained optimization Constrained optimization The regularization theory BYU-ECE Department 2/6/2022

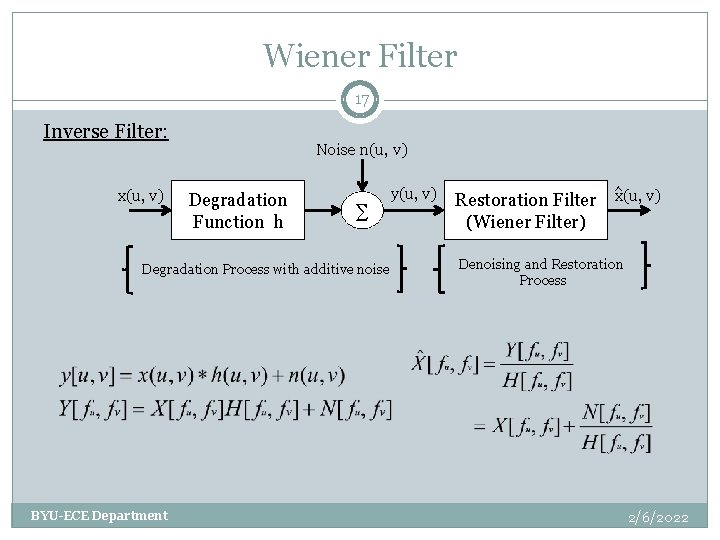
Wiener Filter 17 Inverse Filter: x(u, v) Noise n(u, v) Degradation Function h ∑ Degradation Process with additive noise BYU-ECE Department y(u, v) Restoration Filter (Wiener Filter) x(u, v) Denoising and Restoration Process 2/6/2022

Wiener Filter 18 Wiener Filter: Most neighboring pixels are highly correlated, while widely separated pixels are only loosely correlated. Therefore, the autocorrelation function of typical images generally decreases away from the origin. Power spectrum = Fourier transform of autocorrelation, therefore the power spectrum of an image generally decreases with frequency. Typical noise sources have either a flat power spectrum or one that decreases with frequency more slowly than typical image power spectrum. Therefore, the signal should dominate at low frequencies, while the noise dominates at high frequencies. BYU-ECE Department 2/6/2022

Wiener Filter 19 Wiener Filter: Assumptions: 1. The noise and the image are uncorrelated. 2. Either the noise or the image is zero-mean, and that the intensities in the estimate are a linear function of the intensities in the noisy image. 3. It also assumes that the power spectrum of both the noise and the original image are known Theory (Derivation) v Degradation model BYU-ECE Department 2/6/2022

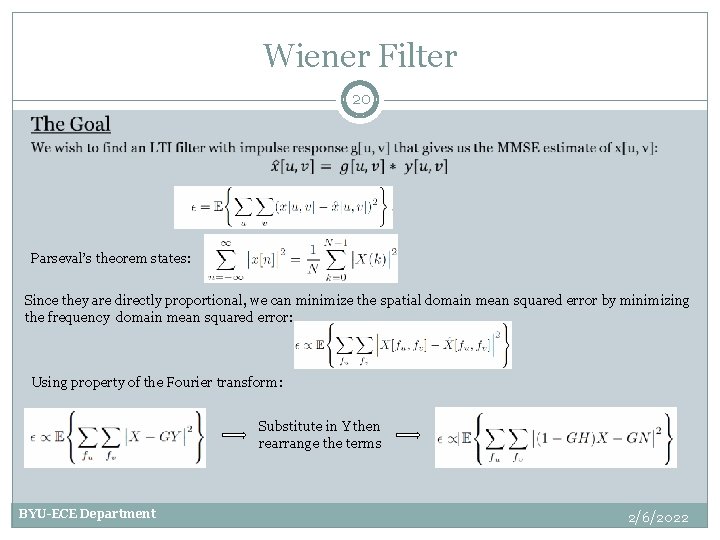
Wiener Filter 20 Parseval’s theorem states: Since they are directly proportional, we can minimize the spatial domain mean squared error by minimizing the frequency domain mean squared error: Using property of the Fourier transform: Substitute in Y then rearrange the terms BYU-ECE Department 2/6/2022

Wiener Filter 21 Using the definition of an absolute square, we get: Multiplying out the terms and distributing the expected value across the sums We assume that the noise is independent of the original image and that either the noise or the image is zero-mean: Where the power spectral densities are defined as: BYU-ECE Department 2/6/2022

Wiener Filter 22 To find the G that minimizes the MSE, we take the derivative with respect to G(fu, fv): Solving for G* gives: HH* = │H│2 Finally, we write the equation in terms of the signal-to-noise Ratio: BYU-ECE Department 2/6/2022

Wiener Filter 23 Wiener Filter Equation: Arranged intuitively: BYU-ECE Department 2/6/2022

Results & Analysis 24 Original image BYU-ECE Department 20 pixel motion blur 2/6/2022

Results & Analysis 25 Original image BYU-ECE Department 20 pixel motion blur, inverse filtered 2/6/2022

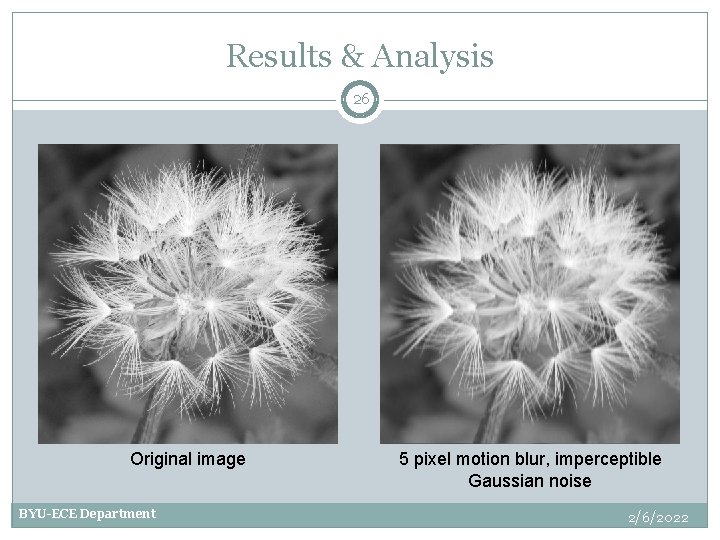
Results & Analysis 26 Original image BYU-ECE Department 5 pixel motion blur, imperceptible Gaussian noise 2/6/2022

Results & Analysis 27 Original image BYU-ECE Department 5 pixel motion blur, imperceptible Gaussian noise, inverse filtered 2/6/2022

Results & Analysis 28 Original image BYU-ECE Department 5 pixel motion blur, imperceptible Gaussian noise, Wiener filtered 2/6/2022

Results & Analysis 29 Original image BYU-ECE Department 15 pixel motion blur, Gaussian noise 2/6/2022

Results & Analysis 30 15 pixel motion blur, Gaussian noise BYU-ECE Department 15 pixel motion blur, Gaussian noise, inverse filtered 2/6/2022

Results & Analysis 31 15 pixel motion blur, Gaussian noise BYU-ECE Department 15 pixel motion blur, Gaussian noise, Wiener filtered 2/6/2022

Results & Analysis 32 3 pixel motion blur, salt and pepper noise BYU-ECE Department 3 pixel motion blur, salt and pepper noise, inverse filtered 2/6/2022

Results & Analysis 33 3 pixel motion blur, salt and pepper noise BYU-ECE Department 3 pixel motion blur, salt and pepper noise, Wiener filtered 2/6/2022

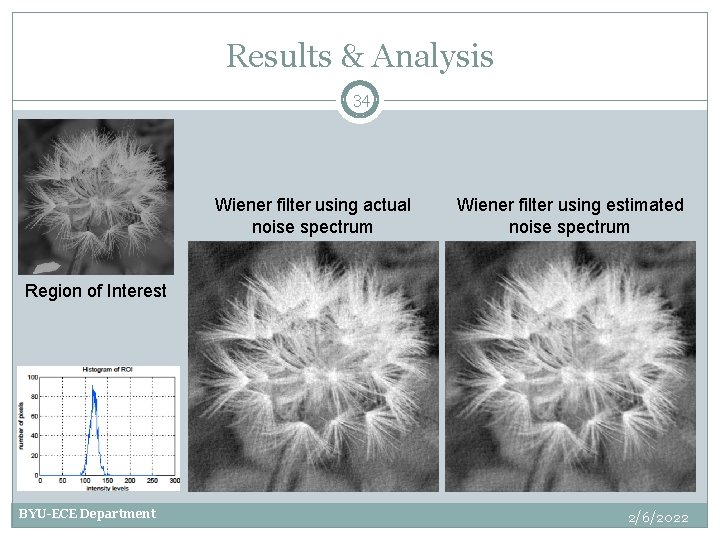
Results & Analysis 34 Wiener filter using actual noise spectrum Wiener filter using estimated noise spectrum Region of Interest BYU-ECE Department 2/6/2022

Conclusions 35 Inverse filter works well with no noise Wiener filter performs much better in the presence of noise Assumes knowledge of degradation function (a common requirement for image restoration algorithms) Assumes knowledge of the power spectra of the noise and original image (less common, makes it less useful) The noise power spectrum can be effectively estimated by analyzing the histogram of an ROI in the noisy image Forms the basis of other more robust restoration approaches BYU-ECE Department 2/6/2022

36 Thank you BYU-ECE Department 2/6/2022