Sticky Note Math Do NOT put your name

Sticky Note Math • Do NOT put your name on the sticky • Solve for X and stick to the white board when you are finished. 4 x = 49 – 3 x

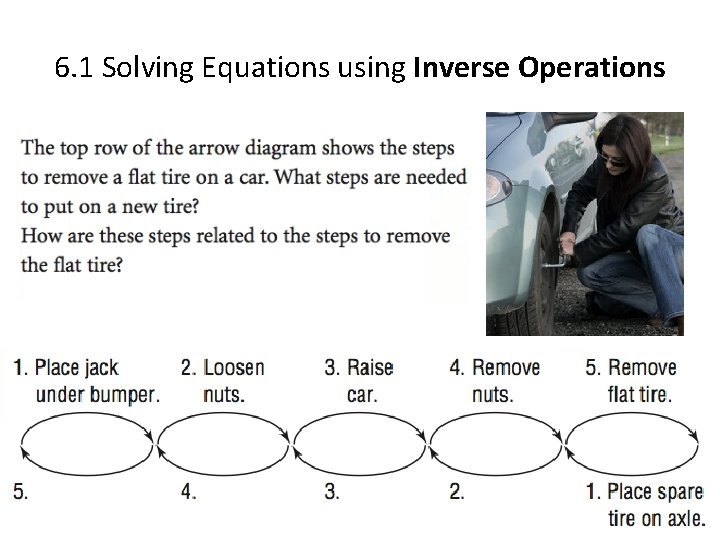
6. 1 Solving Equations using Inverse Operations

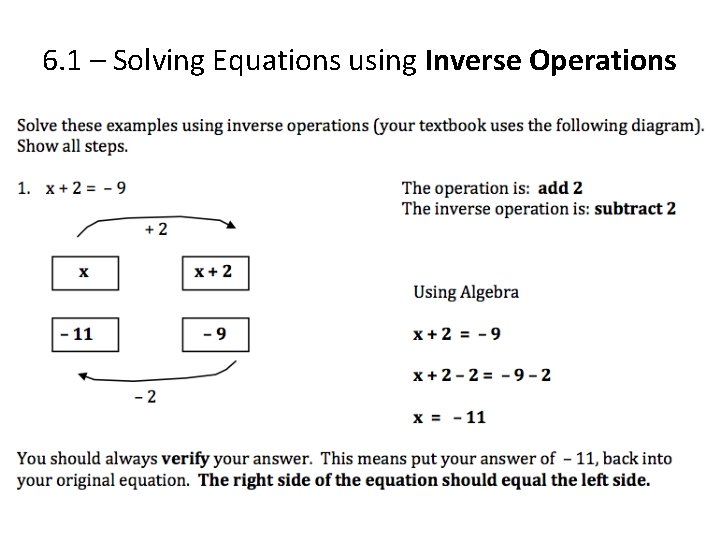
6. 1 – Solving Equations using Inverse Operations

6. 1 – Solving Equations using Inverse Operations

6. 1 – Solving Equations using Inverse Operations

6. 1 – Solving Equations using Inverse Operations

6. 1 – Solving Equations using Inverse Operations • Math Practice for HOMEWORK! • Page 272 • Questions 6 ac, 7, 8 ace, 9 ac, 11 abcd, 12, 14, 15, 17, 18 ace, 19, 20

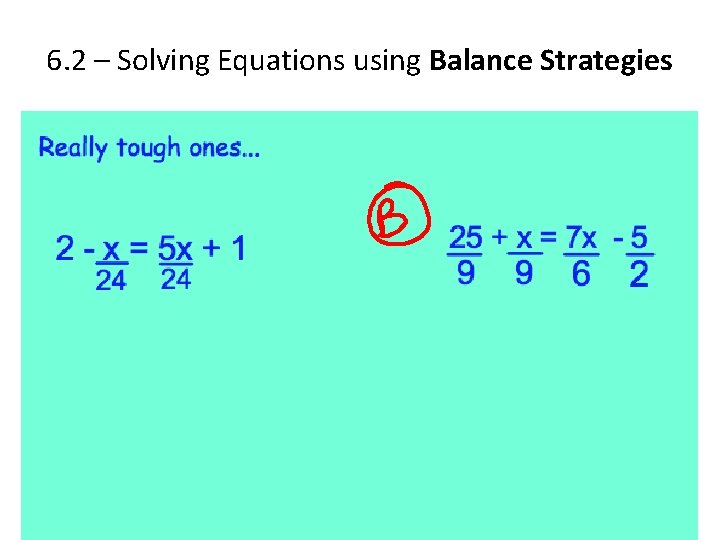
6. 2 – Solving Equations using Balance Strategies

6. 2 – Solving Equations using Balance Strategies

6. 2 – Solving Equations using Balance Strategies

6. 2 – Solving Equations using Balance Strategies

Fraction Review

6. 2 – Solving Equations using Balance Strategies

6. 2 – Solving Equations using Balance Strategies • Math Practice for HOMEWORK • Page 280 -281 • Questions 4, 7 i, 9, 11 ace, 12, 13, 15, 17 cd, 18

6. 2 - Review • Take a few minutes and solve the following: • Once you have your answer verify that it is correct

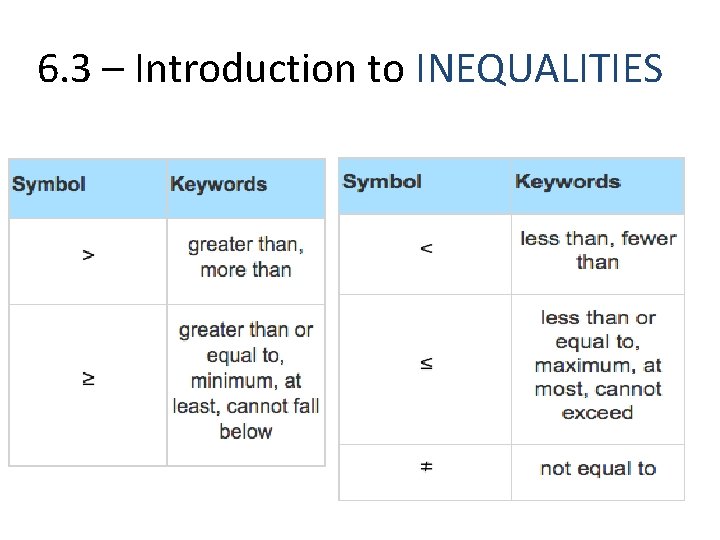
6. 3 – Introduction to INEQUALITIES • A mathematical sentence that does not have an exact value is called an inequality. • An inequality has a set of solutions that meet the requirements of the relationship described. • This differs from an equation, since an equation has only one solution. • For example n < 5 • The solution for an inequality can be written, graphed or shown on a number line.

6. 3 – Introduction to INEQUALITIES • We use inequalities to mode a situation that can be described by a range of numbers instead of a single number. • We use specific symbols to represent that range.

6. 3 – Introduction to INEQUALITIES

6. 3 – Introduction to INEQUALITIES

6. 3 – Introduction to INEQUALITIES • Can you write an inequality that describes the time, t, for which a car could be legally parked?

6. 3 – Introduction to INEQUALITIES • Can you write an inequality that describes the time, t, for which a car could be legally parked? • t ≤ 30

6. 3 – Introduction to INEQUALITIES

6. 3 – Introduction to INEQUALITIES • Choosing variables and writing inequalities: – A. Contest entrants must be at least 18 years old – B. You must have 7 items or less to use the express checkout at Safeway. – C. Scientists have discovered over 400 species of dinosaurs.

6. 3 – Introduction to INEQUALITIES • 1. Assign MEANINGFUL variables • 2. Find Keywords that describe the type of inequality (greater than or more than use >) • 3. Find keywords that describe the operations involved (ie of, times, greater than, product, by would be multiplication) • 4. Write the inequality

6. 3 – Introduction to INEQUALITIES • For her birthday, Skyler received a $500. 00 gift card to Lululemon. She wants to buy a jacket that costs $250. 00 and she would like to spend the rest on tights which are on sale for $20. 00 each. • Write an inequality to describe the maximum number of tights that Skyler can by.

6. 3 – Introduction to INEQUALITIES

6. 3 – Introduction to INEQUALITIES • Representing Inequalities Graphically:

6. 3 – Introduction to INEQUALITIES

6. 3 – Introduction to INEQUALITIES Hint: give yourself LOTS of space and always use a ruler!

6. 3 – Introduction to INEQUALITIES • Math Practice HOMEWORK • Pages 292 – 293 • Questions 4, 5, 7, 8 ace, 9 ace, 11, 12, 14 and 15

6. 3 – Introduction to INEQUALITIES • A) a number greater than 5 would be x >5 • B) you must have 10 items or less to use express • C) you should invite at least 10 friends

6. 3 – Introduction to INEQUALITIES • Be careful when graphing your data – If continuous you can use a line and arrow – If discrete you need to show this using just dots

6. 3 – Review INEQUALITIES

6. 4 – Using addition and subtraction to solve linear inequalities • Understanding Inequalities – Write down any 2 numbers – Put the > or < symbol between them to make a true inequality equation – Choose another number, add that number to each side – is the inequality still true? – Choose another number, subtract that number from each side – is the inequality still true?

6. 4 – Using addition and subtraction to solve linear inequalities • When the same number is added or subtracted from each side of an inequality is the resulting inequality still true? • Explain using the example x +5 > 11

6. 4 – Using addition and subtraction to solve linear inequalities • We can use a number line to see that YES when the same number is added (or subtracted) from each side of an inequality the resulting inequality is still true.

6. 4 – Using addition and subtraction to solve linear inequalities • To solve an inequality use the same strategy as for solving an equation: – Gather like terms – Isolate the variable using opposite operations

6. 4 – Using addition and subtraction to solve linear inequalities

6. 4 – Using addition and subtraction to solve linear inequalities

6. 4 – Using addition and subtraction to solve linear inequalities Problem Solving • Ms. Watson plans to board her snake while she is away on vacation. – Boarding house A charges $90 plus $5/day – Boarding house B charges $100 plus $4/day • For how many days must Ms. Watson board her snake for A to be cheaper than B? a) Write an inequality b)Solve c) Graph the solution

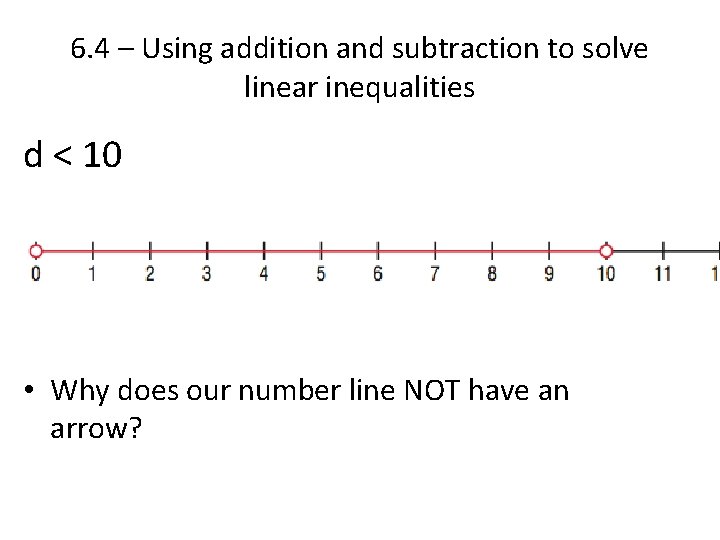
6. 4 – Using addition and subtraction to solve linear inequalities d < 10 • Why does our number line NOT have an arrow?

6. 4 – Using addition and subtraction to solve linear inequalities • Math Practice for HOMEWORK • Pages 298 -299 • Questions 6, 7, 8 ace, 9 ace, 13 and 14 • Remember to use a ruler And give yourself lots of room

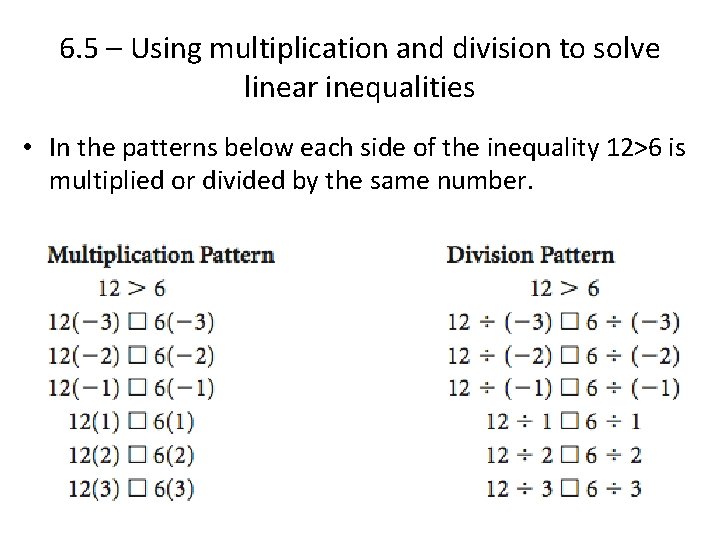
6. 5 – Using multiplication and division to solve linear inequalities • In the patterns below each side of the inequality 12>6 is multiplied or divided by the same number.

6. 5 – Using multiplication and division to solve linear inequalities • When Multiplying or Dividing inequalities the rule is: When you multiply or divide by a NEGATIVE number you must REVERSE the inequality.

6. 5 – Using multiplication and division to solve linear inequalities • Try these and verify that your answer is correct: A) -2 w < 20 B) -4 w + 5 > -3

6. 5 – Using multiplication and division to solve linear inequalities • Try something a bit meatier, again verify your answer is correct. If you finish early graph your results. -2(3 -1. 5 n) < 3(2 -n)

6. 5 – Using multiplication and division to solve linear inequalities Problem Solve • A super-slide ride charges $1. 25 to rent a mat and $0. 75 per ride. Phil has $10. 25. How many rides can he go on? A) Write an inequality B) Solve the inequality C) Graph the solution

6. 4 – Using multiplication and division to solve linear inequalities • Math Practice for HOMEWORK • Pages 305 – 306 • Question # 4, 6, 7 a, 9, 10, 11 c, 12 ac, 17 • The Unit test on page 310 is Assignment #2 for Unit 6. It is due ____ our math final for Unit 6 will be: April _____.