Stereometria rezy telies Miroslav ikli 3 F 20112012

Stereometria, rezy telies Miroslav Šiklóši, 3. F 2011/2012 Gymnázium J. G. Tajovského, B. Bystrica

Základné pojmy • Stereometria - geometria v priestore • Základnými stereometrickými pojmami sú bod, priamka a rovina • Bod - bezrozmerný geometrický útvar - označujeme veľkými tlačenými písmenami (A, B, C, . . . ) • Priamka - jednorozmerný geometrický útvar - označujeme malými písanými písmenami (a, b, c, . . . ) • Rovina - dvojrozmerný geometrický útvar - označujeme malými písmenami gréckej abecedy (α, β, γ, . . . )

Rovina je jednoznačne určená • tromi rôznymi bodmi • priamkou a bodom, ktorý neleží na tejto priamke • dvoma rovnobežnými, navzájom rôznymi priamkami • dvoma rôznobežnými priamkami

Niektoré stereometrické vzťahy • Ľubovoľnými dvomi navzájom rôznymi bodmi A, B v priestore prechádza práve jedna priamka. • Priamkou p a bodom A, ktorý na nej neleží, prechádza práve jedna rovina. • Daným bodom v priestore je možné viesť jedinú rovnobežku rovnobežnú s danou priamkou. • Ak priamka a je rovnobežná s priamkou b, priamka b je rovnobežná s priamkou c, tak aj priamka a bude rovnobežná s priamkou c. • Daným bodom možno viesť k danej rovine práve jednu kolmicu.

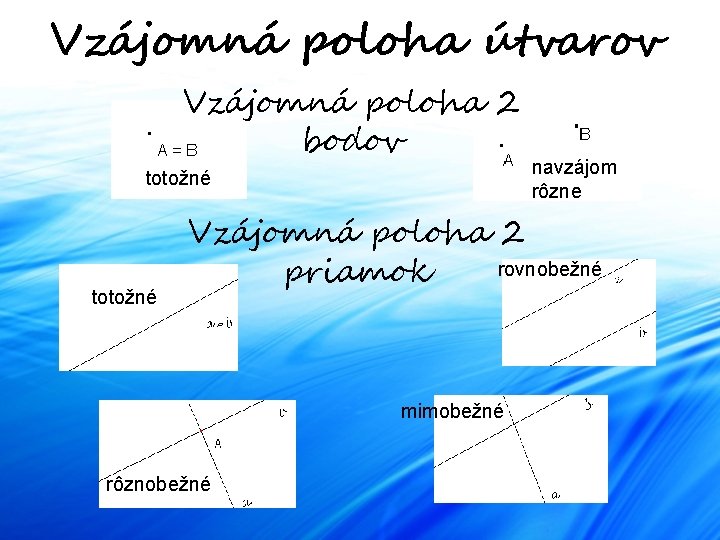
Vzájomná poloha útvarov Vzájomná poloha 2 bodov totožné navzájom rôzne Vzájomná poloha 2 rovnobežné priamok mimobežné rôznobežné

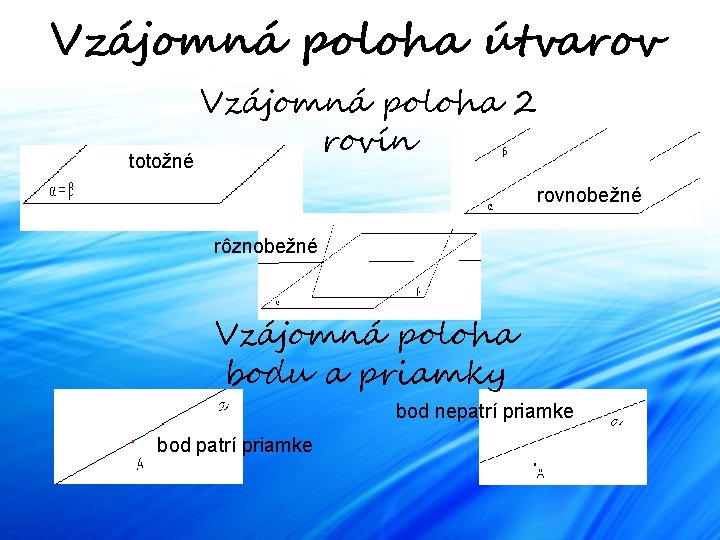
Vzájomná poloha útvarov totožné Vzájomná poloha 2 rovín rovnobežné rôznobežné Vzájomná poloha bodu a priamky bod nepatrí priamke bod patrí priamke

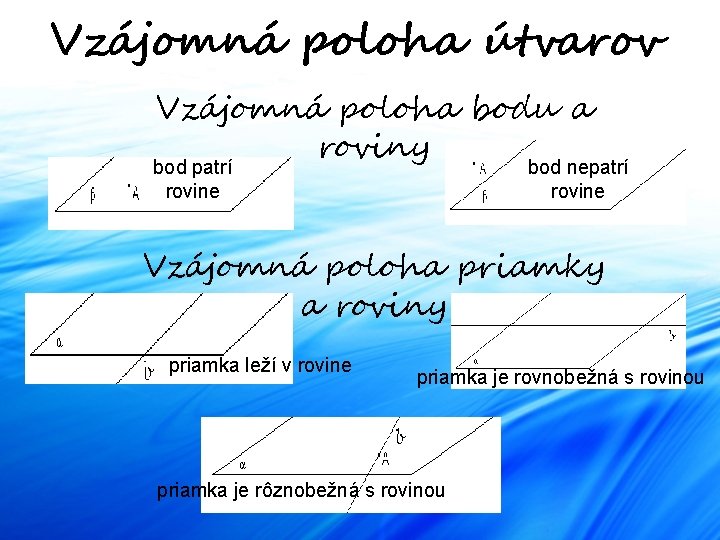
Vzájomná poloha útvarov Vzájomná poloha bodu a roviny bod patrí rovine bod nepatrí rovine Vzájomná poloha priamky a roviny priamka leží v rovine priamka je rovnobežná s rovinou priamka je rôznobežná s rovinou

Rezy telies • Rez telesa je prienik telesa a roviny. Rezom je rovinný útvar, ktorého hranica je prienik telesa s rovinou rezu. Hranica rezu sa skladá z prienikov roviny rezu so stenami telesa. • Využívané dôsledky pri konštrukcii rezu: – Hľadáme dva body ležiace v jednej rovine, lebo nimi je jednoznačne určená priamka. – V prípade rovnobežnostena využijeme vetu: Ak je rovina rovnobežná s dvomi rovnobežnými rovinami, tak ich pretína v rovnobežných priamkach. – Ak máme len jeden bod v rovine, snažíme sa nájsť ďalší bod predĺžením hrán telesa tak, aby sme nimi mohli zostrojiť priamku.

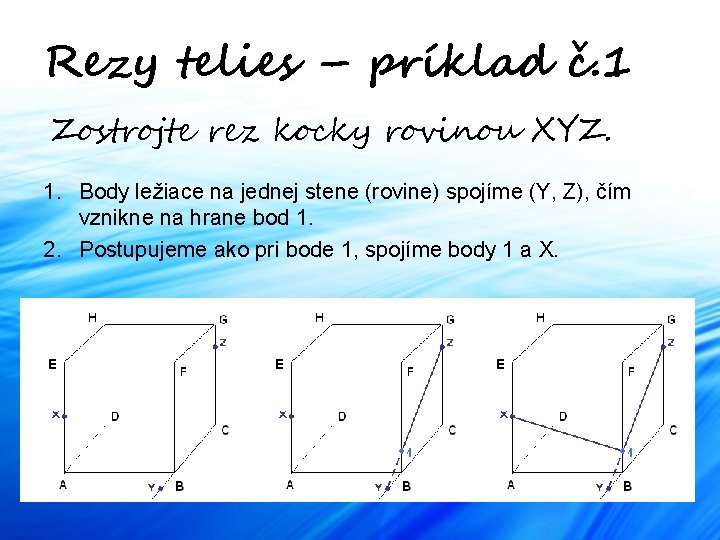
Rezy telies – príklad č. 1 Zostrojte rez kocky rovinou XYZ. 1. Body ležiace na jednej stene (rovine) spojíme (Y, Z), čím vznikne na hrane bod 1. 2. Postupujeme ako pri bode 1, spojíme body 1 a X.

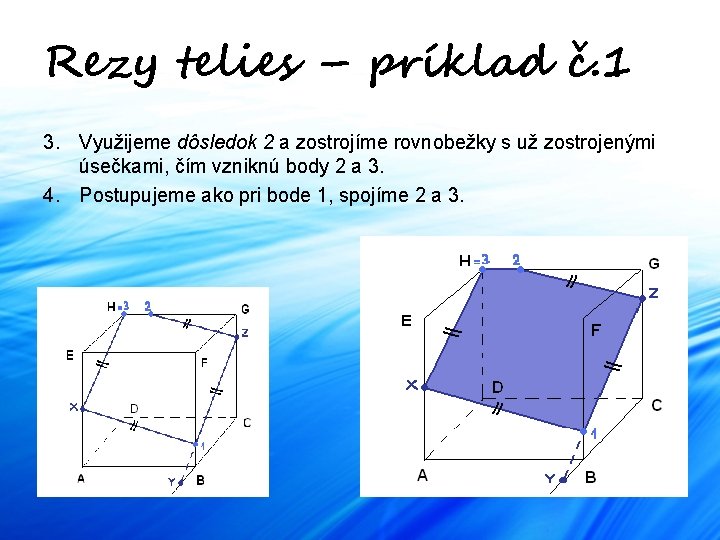
Rezy telies – príklad č. 1 3. Využijeme dôsledok 2 a zostrojíme rovnobežky s už zostrojenými úsečkami, čím vzniknú body 2 a 3. 4. Postupujeme ako pri bode 1, spojíme 2 a 3.

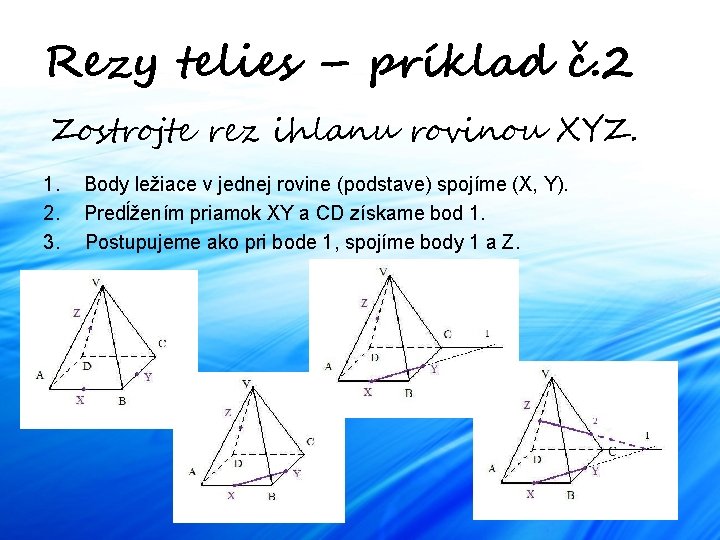
Rezy telies – príklad č. 2 Zostrojte rez ihlanu rovinou XYZ. 1. 2. 3. Body ležiace v jednej rovine (podstave) spojíme (X, Y). Predĺžením priamok XY a CD získame bod 1. Postupujeme ako pri bode 1, spojíme body 1 a Z.

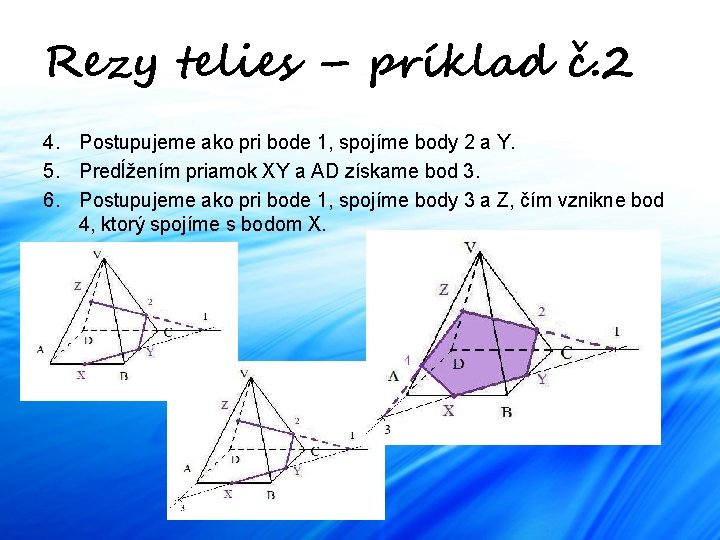
Rezy telies – príklad č. 2 4. Postupujeme ako pri bode 1, spojíme body 2 a Y. 5. Predĺžením priamok XY a AD získame bod 3. 6. Postupujeme ako pri bode 1, spojíme body 3 a Z, čím vznikne bod 4, ktorý spojíme s bodom X.

Ďakujem za pozornosť!