Steinerov pouak i dinamiki moment inercije geometrijskih tijela

Steinerov poučak i dinamički moment inercije geometrijskih tijela Dino Alegić, mag. ing. mech. Strojarska tehnička škola Osijek

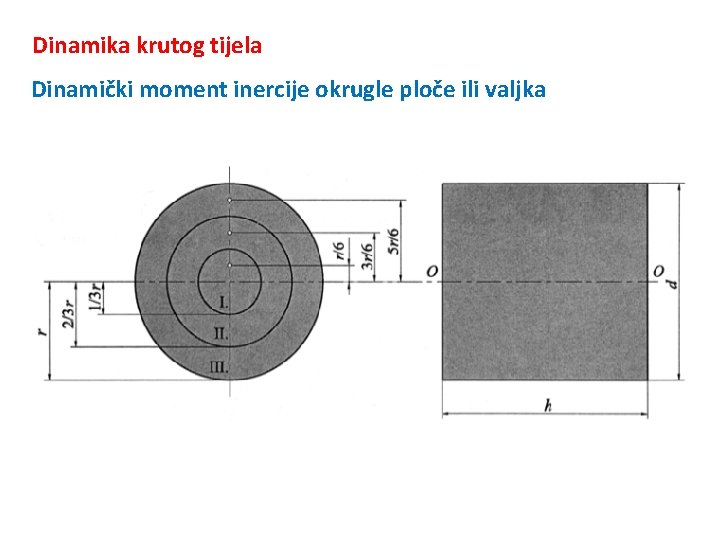
Dinamika krutog tijela Dinamički moment inercije okrugle ploče ili valjka

Dinamika krutog tijela Ako se uzme da je valjak prema slici razdijeljen na 3 dijela polumjera r/3, 2 r/3 i r , tada srednji polumjeri pojedinih dijelova iznose: Izvedeno volumeni pojedinih dijelova su:

Dinamika krutog tijela Budući da su mase razmjerne volumenima, masa je: I dio: III dio: gdje je m masa cijelog valjka Izvedeni izraz za dinamički moment inercije punog valjka ili okrugle ploče je:

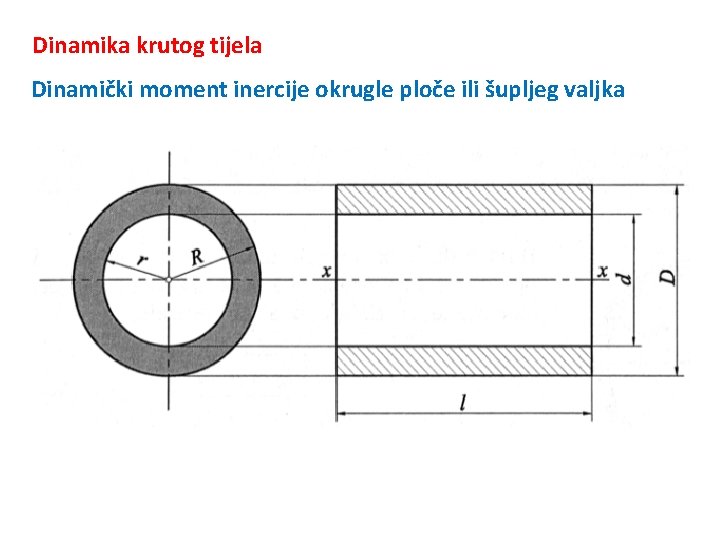
Dinamika krutog tijela Dinamički moment inercije okrugle ploče ili šupljeg valjka

Dinamika krutog tijela Dinamički moment inercije za os x-x šupljeg valjka prema slici dobije se tako da dinamički moment inercije punog valjka umanjimo za dinamički moment inercije šupljine: gdje je m 2 masa punog valjka, a m 1 masa valjka koji čini šupljina. Dakle masa šupljeg valjka iznosi: Masa izražena produktom gustoće ρ i volumena je:

Dinamika krutog tijela Izvedeni izraz za dinamički moment inercije šupljeg valjka ili okrugle ploče je:

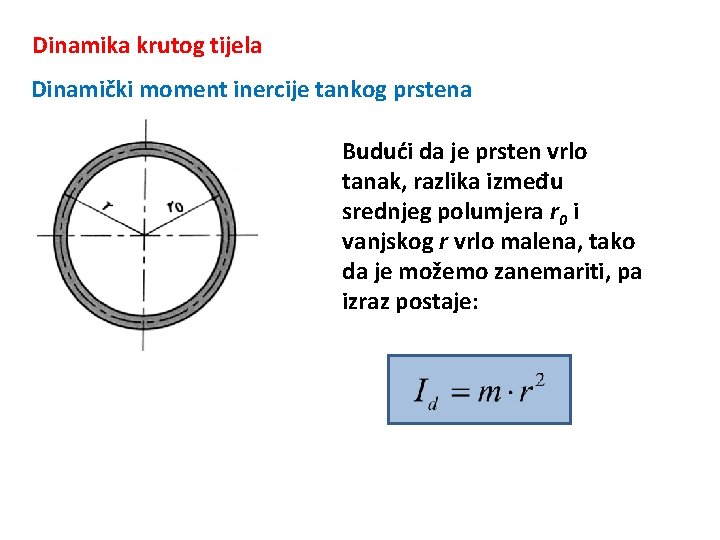
Dinamika krutog tijela Dinamički moment inercije tankog prstena Budući da je prsten vrlo tanak, razlika između srednjeg polumjera r 0 i vanjskog r vrlo malena, tako da je možemo zanemariti, pa izraz postaje:

Dinamika krutog tijela Dinamički moment inercije kugle Konačan izraz za dinamički moment inercije kugle je: gdje je: m – masa kugle ; R – polumjer kugle. ( kg )

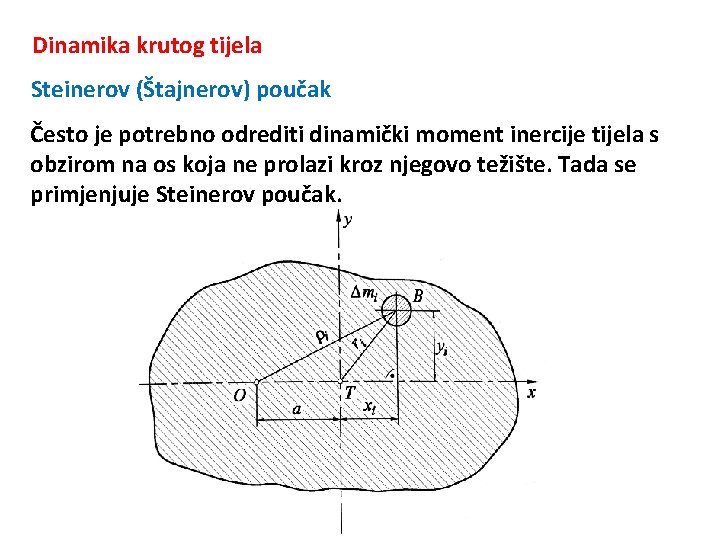
Dinamika krutog tijela Steinerov (Štajnerov) poučak Često je potrebno odrediti dinamički moment inercije tijela s obzirom na os koja ne prolazi kroz njegovo težište. Tada se primjenjuje Steinerov poučak.

Dinamika krutog tijela Steinerov (Štajnerov) poučak Na slici je prikazan presjek nekog tijela čije je težište u točki T. Treba pronaći dinamički moment inercije za os koja prolazi kroz točku O i na udaljenosti a od težišta T. Osi položene kroz O i T su međusobno paralelne i okomite na ravninu slike. Dinamički moment inercije mase tijela s obzirom na os koja ne prolazi kroz njegovo težište, a paralelna je s osi koja prolazi kroz težište, jednak je vlastitom dinamičkom momentu inercije uvećanom za produkt mase tijela i kvadrata udaljenosti osi od težišta. Konačan izraz glasi:

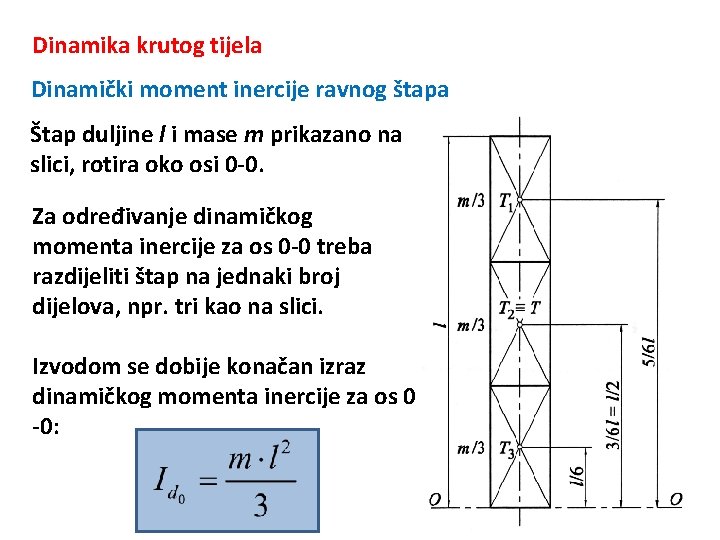
Dinamika krutog tijela Dinamički moment inercije ravnog štapa Štap duljine l i mase m prikazano na slici, rotira oko osi 0 -0. Za određivanje dinamičkog momenta inercije za os 0 -0 treba razdijeliti štap na jednaki broj dijelova, npr. tri kao na slici. Izvodom se dobije konačan izraz dinamičkog momenta inercije za os 0 -0:

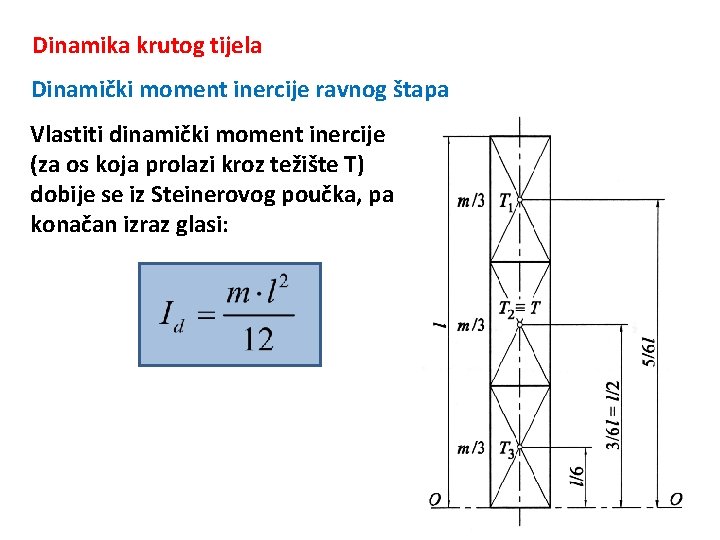
Dinamika krutog tijela Dinamički moment inercije ravnog štapa Vlastiti dinamički moment inercije (za os koja prolazi kroz težište T) dobije se iz Steinerovog poučka, pa konačan izraz glasi: