Steiner tree LP xe 1 if edge e


- Slides: 17

Steiner tree LP xe = 1 if edge e is included in the Steiner tree. Min. e cexe s. t. (primal) eÎ (S) xe ≥ 1 terminal SÍV: SÇT≠Æ, TS≠Æ xe Î {0, 1} xe ≥ 0 (1) terminal S Relax (1) to xe ≥ 0 to get an LP.

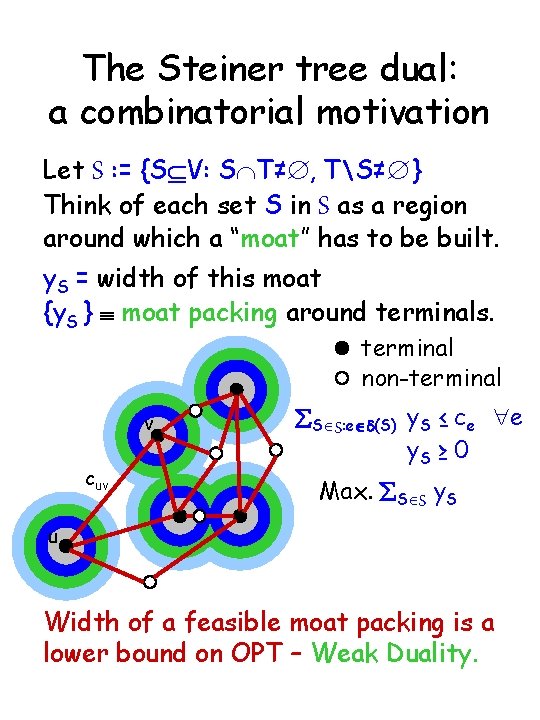
The Steiner tree dual: a combinatorial motivation Let S : = {SÍV: SÇT≠Æ, TS≠Æ } Think of each set S in S as a region around which a “moat” has to be built. y. S = width of this moat {y. S } º moat packing around terminals. terminal non-terminal v cuv SÎS: eÎ (S) y. S ≤ ce "e y. S ≥ 0 Max. SÎS y. S u Width of a feasible moat packing is a lower bound on OPT – Weak Duality.

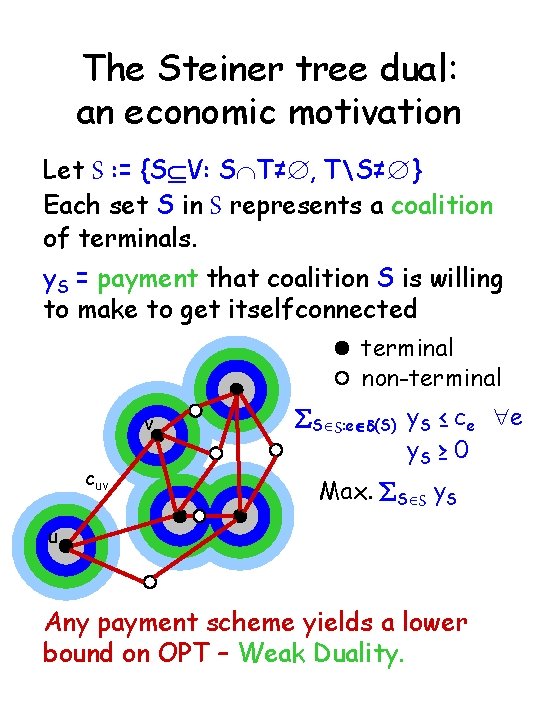
The Steiner tree dual: an economic motivation Let S : = {SÍV: SÇT≠Æ, TS≠Æ } Each set S in S represents a coalition of terminals. y. S = payment that coalition S is willing to make to get itselfconnected terminal non-terminal v cuv SÎS: eÎ (S) y. S ≤ ce "e y. S ≥ 0 Max. SÎS y. S u Any payment scheme yields a lower bound on OPT – Weak Duality.

Primal-dual algorithm for Steiner tree Let S : = {SÍV: SÇT≠Æ, TS≠Æ } Max. SÎS y. S (dual) Min. e cexe (primal) SÎS: eÎ (S) y. S ≤ ce "e eÎ (S) xe ≥ 1 SÎS y. S ≥ 0 xe ≥ 0 Build an integer feasible primal solution x and a dual feasible solution y 1. Initialize F =Æ, y. S = 0 for all SÎS. 2. V = minimal violated sets 3. = {SÎS: S is minimal s. t. d(S)ÇF=Æ } 2. While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. 3. (Reverse delete) Consider edges of F in reverse order, drop e if F{e} is feasible.

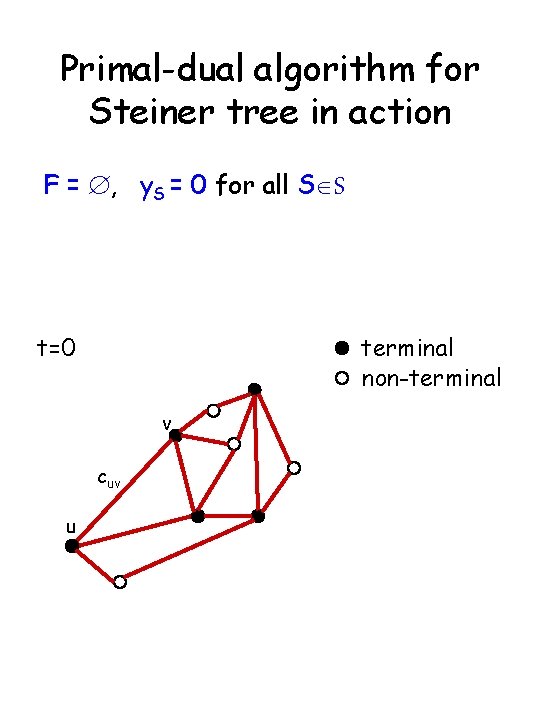
Primal-dual algorithm for Steiner tree in action F = Æ, y. S = 0 for all SÎS t=0 terminal non-terminal v cuv u

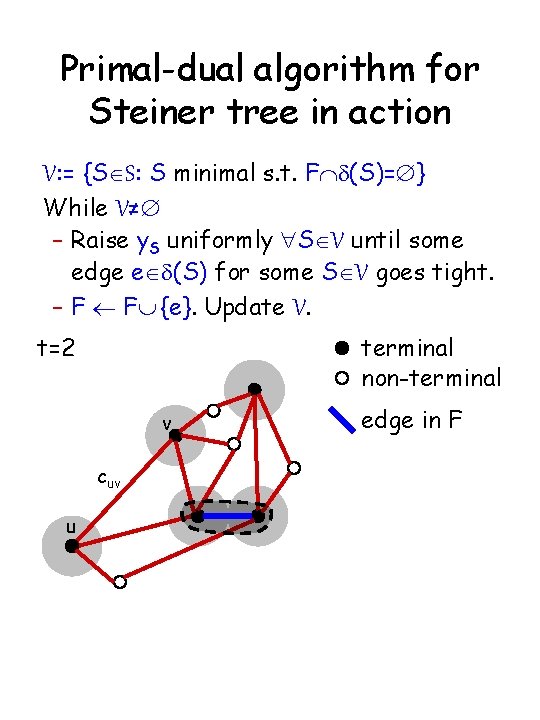
Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=2 t=1 terminal non-terminal v cuv u edge in F

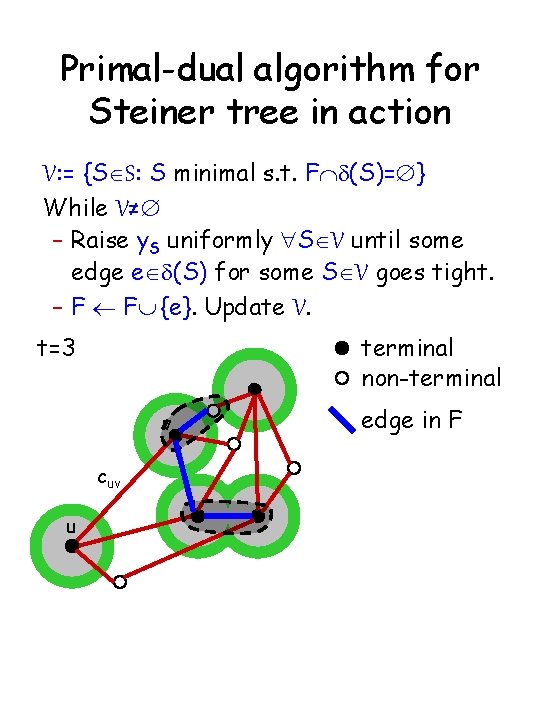
Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=3 terminal non-terminal v cuv u edge in F

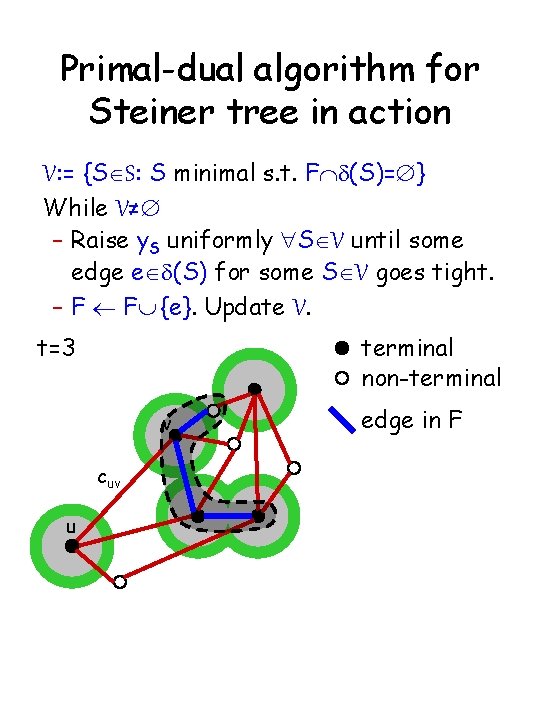
Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=3 terminal non-terminal v cuv u edge in F

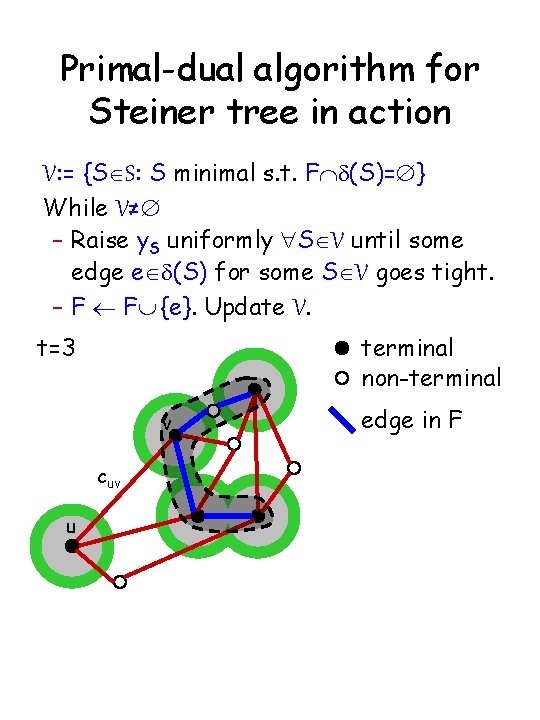
Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=3 terminal non-terminal v cuv u edge in F

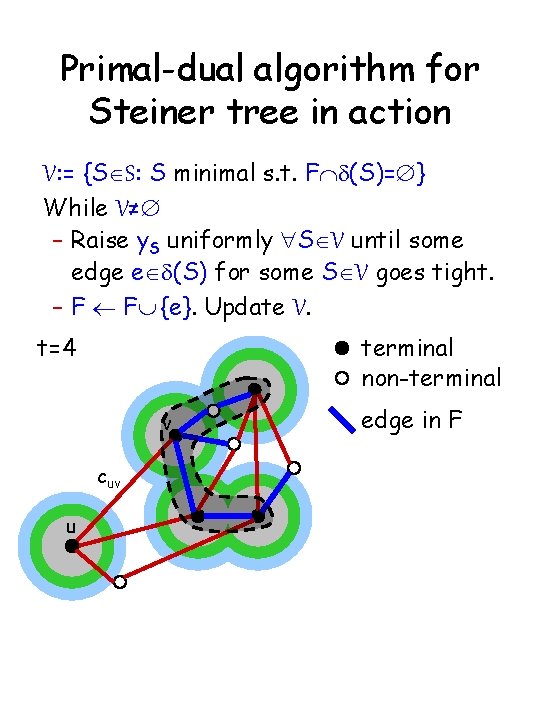
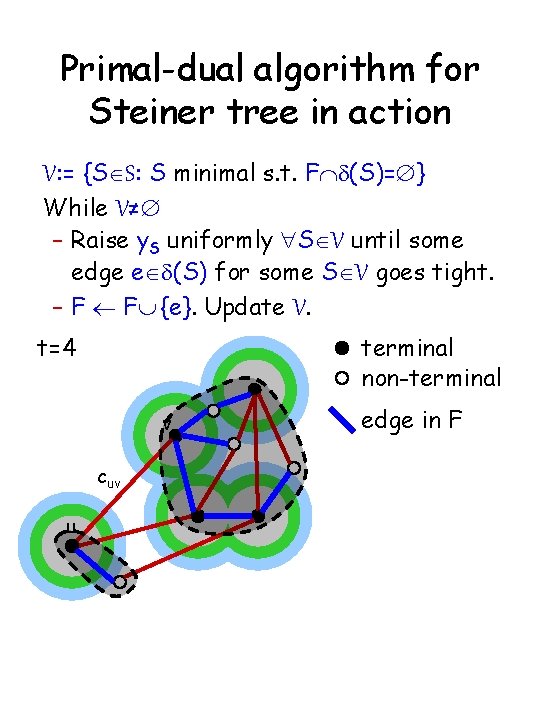
Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=4 terminal non-terminal v cuv u edge in F

Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=4 terminal non-terminal v cuv u edge in F

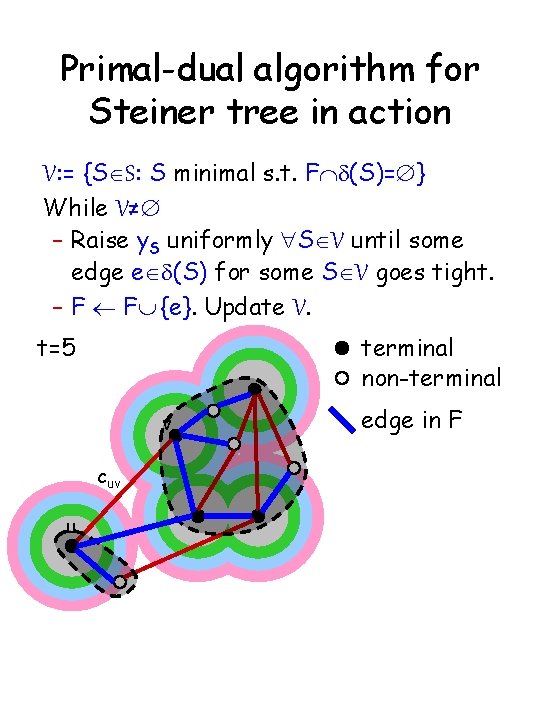
Primal-dual algorithm for Steiner tree in action V: = {SÎS: S minimal s. t. FÇd(S)=Æ} While V≠Æ – Raise y. S uniformly "SÎV until some edge eÎd(S) for some SÎV goes tight. – F ¬ FÈ {e}. Update V. t=5 terminal non-terminal v cuv u edge in F

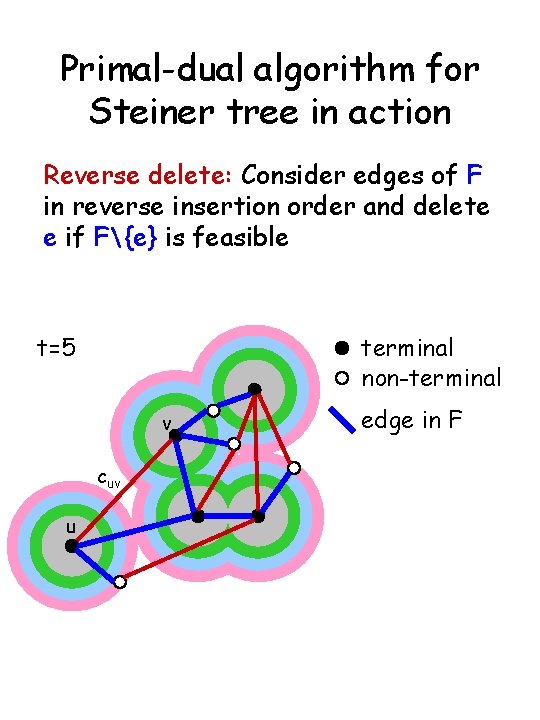
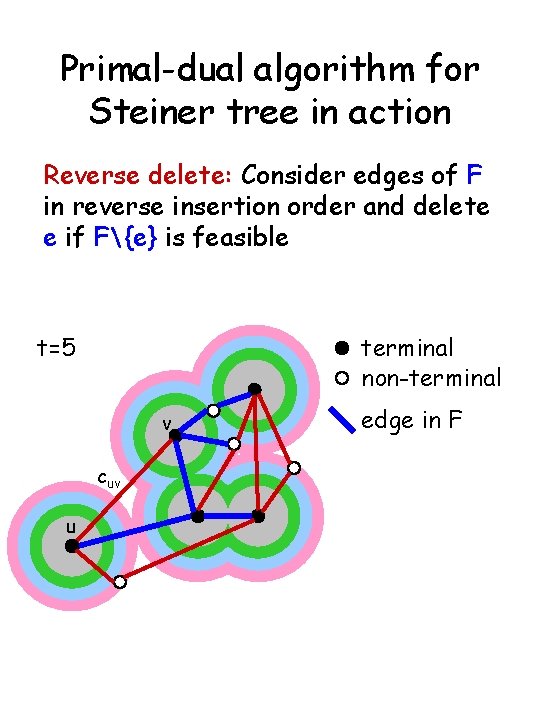
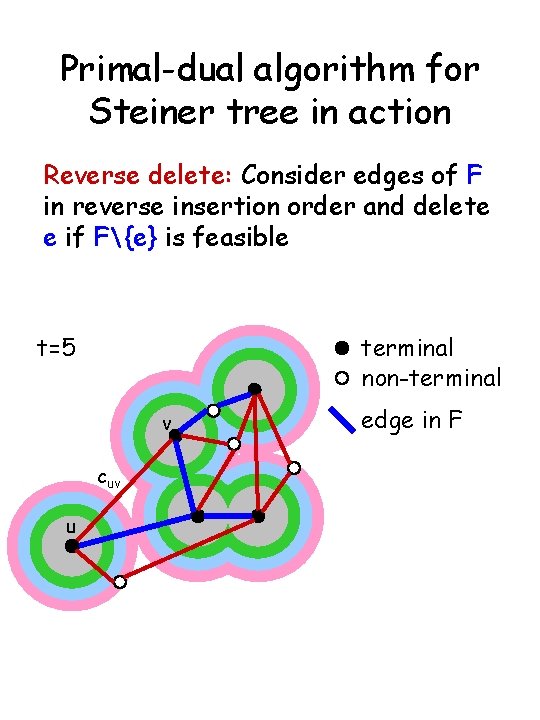
Primal-dual algorithm for Steiner tree in action Reverse delete: Consider edges of F in reverse insertion order and delete e if F{e} is feasible t=5 terminal non-terminal v cuv u edge in F

Primal-dual algorithm for Steiner tree in action Reverse delete: Consider edges of F in reverse insertion order and delete e if F{e} is feasible t=5 terminal non-terminal v cuv u edge in F

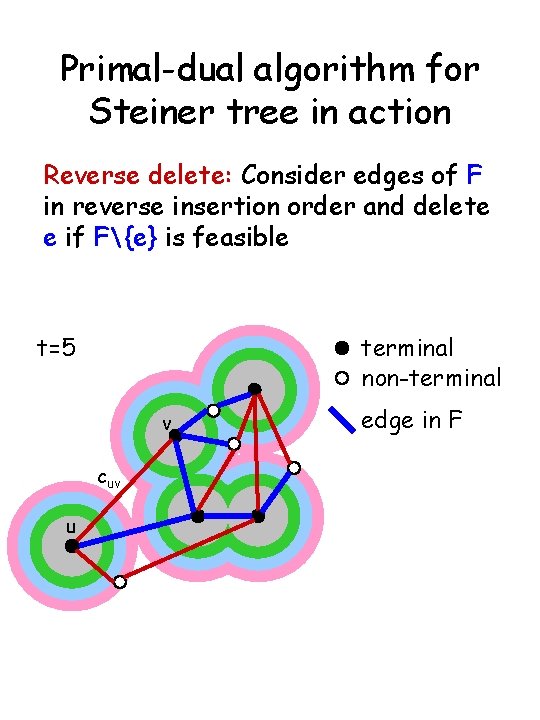
Primal-dual algorithm for Steiner tree in action Reverse delete: Consider edges of F in reverse insertion order and delete e if F{e} is feasible t=5 terminal non-terminal v cuv u edge in F

Primal-dual algorithm for Steiner tree in action Reverse delete: Consider edges of F in reverse insertion order and delete e if F{e} is feasible t=5 terminal non-terminal v cuv u edge in F

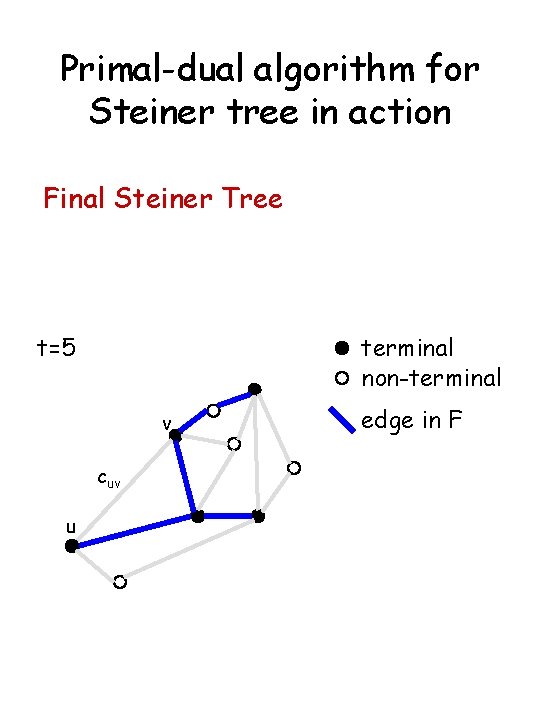
Primal-dual algorithm for Steiner tree in action Final Steiner Tree t=5 terminal non-terminal v cuv u edge in F