Std 8 th Chapter 3 MATHEMATICS m l

Std - 8 th Chapter 3 MATHEMATICS m l n

Parallel Lines q Revision q Drawing parallel Lines q To check whether given lines are parallel or not q Lines parallel to the same line q Lines perpendicular to the same line q The intercept and its properties q Dividing a line segment into equal parts q Dividing a line segment into given ratio

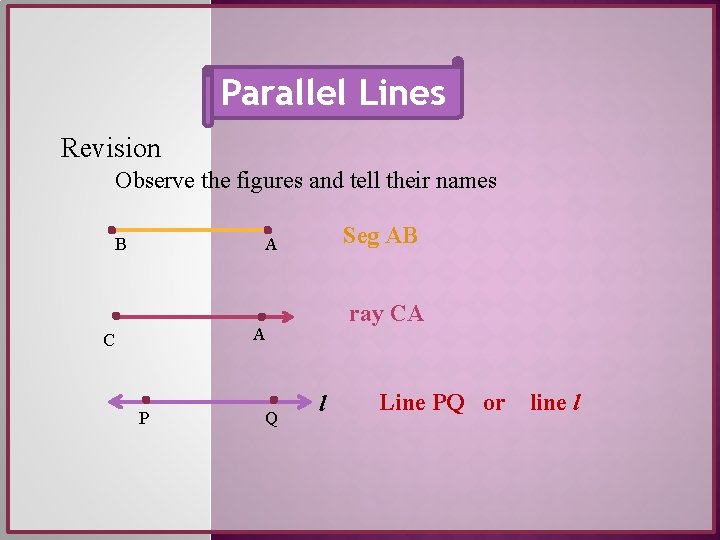
Parallel Lines Revision Observe the figures and tell their names B Seg AB A ray CA A C P Q l Line PQ or line l

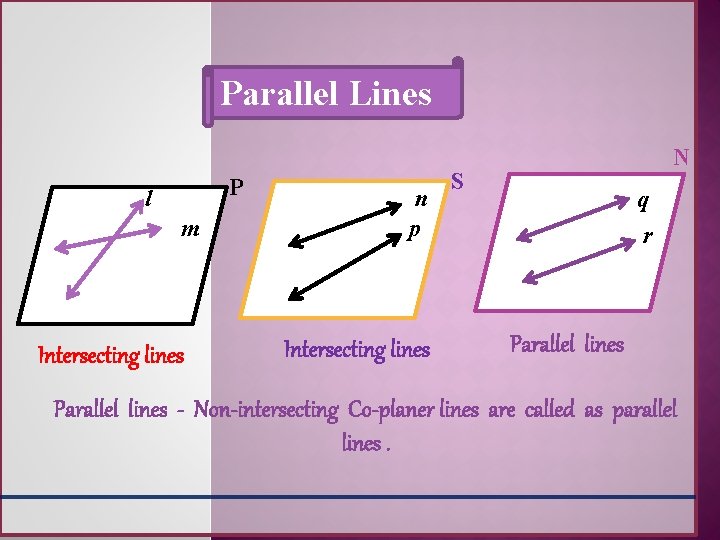
Parallel Lines P l m Intersecting lines n p Intersecting lines N S q r Parallel lines - Non-intersecting Co-planer lines are called as parallel lines.

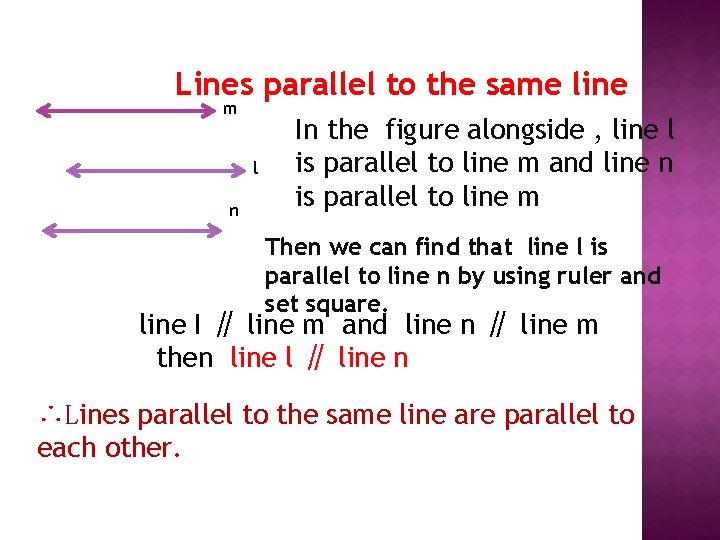
Lines parallel to the same line m l n In the figure alongside , line l is parallel to line m and line n is parallel to line m Then we can find that line l is parallel to line n by using ruler and set square. line I ∥ line m and line n ∥ line m then line l ∥ line n ∴Lines parallel to the same line are parallel to each other.

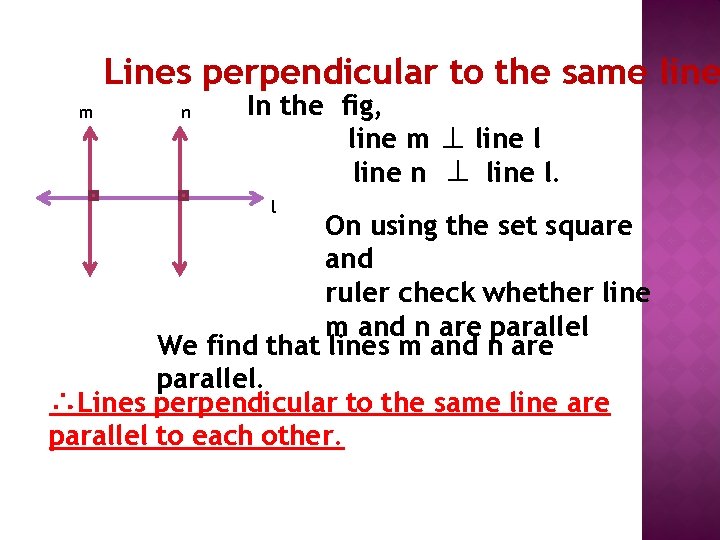
Lines perpendicular to the same line m n In the fig, line m ⊥ line l line n ⊥ line l. l On using the set square and ruler check whether line m and n are parallel We find that lines m and n are parallel. ∴Lines perpendicular to the same line are parallel to each other.

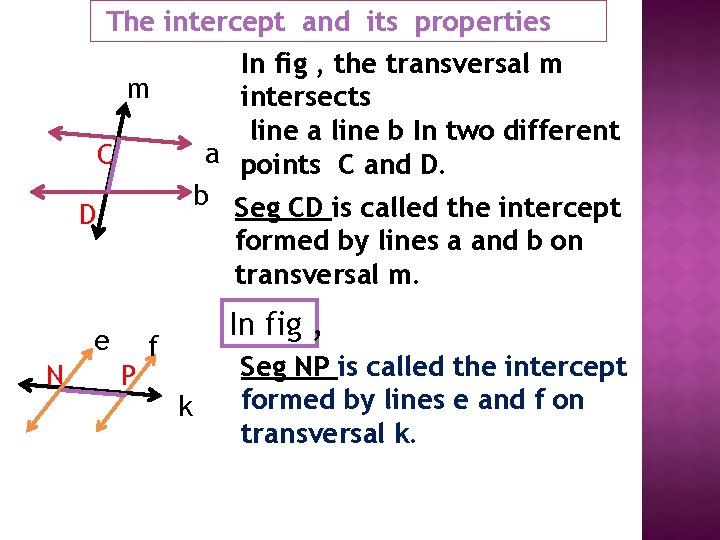
D The intercept and its properties In fig , the transversal m m intersects line a line b In two different a points C and D. C b Seg CD is called the intercept formed by lines a and b on transversal m. e N P In fig , f k Seg NP is called the intercept formed by lines e and f on transversal k.

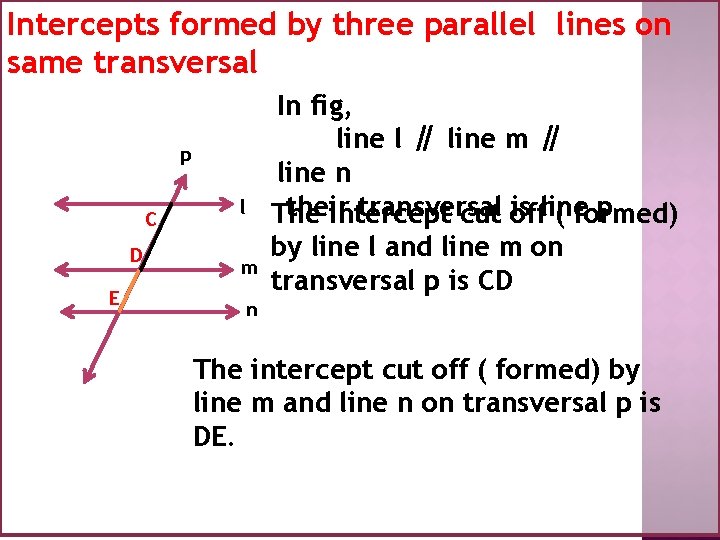
Intercepts formed by three parallel lines on same transversal p C D E l m In fig, line l ∥ line m ∥ line n their transversal is line p The intercept cut off ( formed) by line l and line m on transversal p is CD n The intercept cut off ( formed) by line m and line n on transversal p is DE.

The properties of the parallel lines and their transversavls with respect to intercepts. p A B C Compare the lengths of intercept AB and intercept BC. q ɺ(AB) =ɺ(BC) ∴seg AB ≅ seg BC m Now, compare the lengths of intercept n DE and intercept EF ɺ(DE) = ɺ(EF) ∴seg DE ≅ seg EF l D E F It means that , if the intercepts formed by three parallel lines on any one transversal are congruent , the intercepts they form on any other transversal are also congruent.

The properties of the parallel lines and their transversavls with respect to intercepts. x y z p C D E q In fig , line x , y and z are parallel lin Lines p and q are transversal. Seg CD , seg DE , seg LM and seg MN M are the intercepts. Compare the lengths of seg CD and N seg DE We find that , Similarly, ∴From(I)and(II) L ∴ The ratio of the lengths of intercepts made by three parallel lines on one transversal and the ratio of the lengths of the corresponding intercepts made by the same parallel lines on any other transversal are equal.

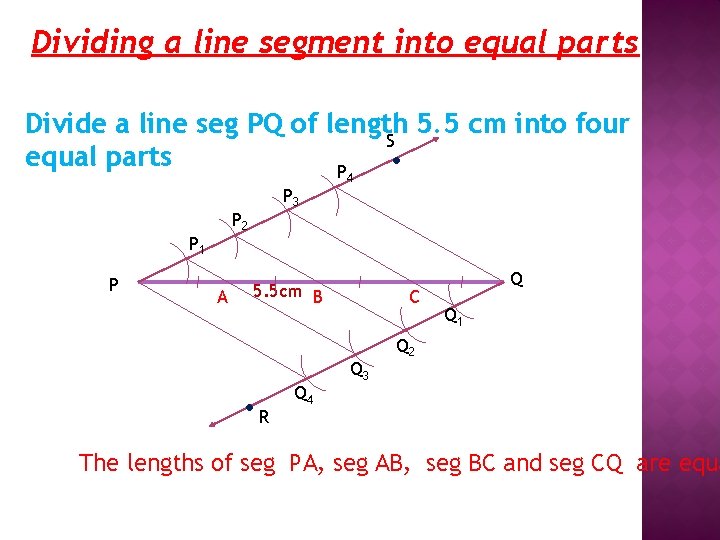
Dividing a line segment into equal parts Divide a line seg PQ of length 5. 5 cm into four S equal parts P P 2 P 1 P P 3 A 4 5. 5 cm B . R Q 4 . C Q 3 Q Q 1 Q 2 The lengths of seg PA, seg AB, seg BC and seg CQ are equa

Dividing a line segment in given ratio Divide a line seg AB of length 7 cm in the ratio 3: 2 Hence, first we divide seg AB in five equal parts Here, 3+2=5 A 4 A 3 M . A 2 A 1 A A 5 ѳ Q 7 cm P . N B 5 B 4 R B 3 S B 2 ѳ B B 1 Thus point R divides seg AB in the ratio 3: 2

Y B D E T N. E S R P e l a ). d E. B. g , c n i S a. P y. a s (B l r a y M d i V ) h. t D a n K ( v a i r r i a a s h a B w i A r h S