STATYSTYKA OPISOWA 1 1 Podstawowe pojcia statystyki Statystyka

STATYSTYKA OPISOWA 1

1. Podstawowe pojęcia statystyki Statystyka to nauka o ilościowych metodach badania własności zbiorowości. Zajmuje się badaniem, czyli gromadzeniem, porządkowaniem i analizowaniem danych o własnościach zbiorowości. Populacja statystyczna (zbiorowość) jest to zbiór elementów podlegających badaniu statystycznemu. Jednostka statystyczna to każdy element populacji statystycznej. Liczebność populacji to liczba jednostek statystycznych. Próba statystyczna to podzbiór populacji, zbiór tych jednostek statystycznych, które bezpośrednio poddajemy badaniu statystycznemu i które w określony sposób zostały wybrane z populacji. Cecha statystyczna (zmienna) to właściwość elementów populacji będąca przedmiotem badania statystycznego. 2

Przykład 1. 1. Wśród studentów AMW przeprowadzono ankietę, pytając o: wzrost, czas dojazdu na uczelnię, płeć. Populacja – zbiór wszystkich studentów AMW. Jednostka statystyczna – student AMW. Cechy statystyczne – wzrost, czas dojazdu na uczelnię, płeć. 3

Klasyfikacja cech statystycznych: - cecha mierzalna: - ciągła – może przyjmować każdą wartość z pewnego przedziału zmienności, np. wiek, miesięczny dochód pracownika, waga ciała, wzrost, itp. - skokowa –może przyjmować skończoną lub przeliczalną liczbę wartości, w pewnym przedziale zmienności może przyjąć tylko niektóre wartości, np. liczba dzieci w rodzinie, liczba egzaminów w sesji itp. - quasi-ciągła – to cecha skokowa, która ze względu na dużą liczbę wartości traktowana jest jak cecha ciągła. - cecha niemierzalna: cecha, której warianty (kategorie) opisane są słownie, np. kolor oczu, rodzaj wykształcenia, itp. . 4

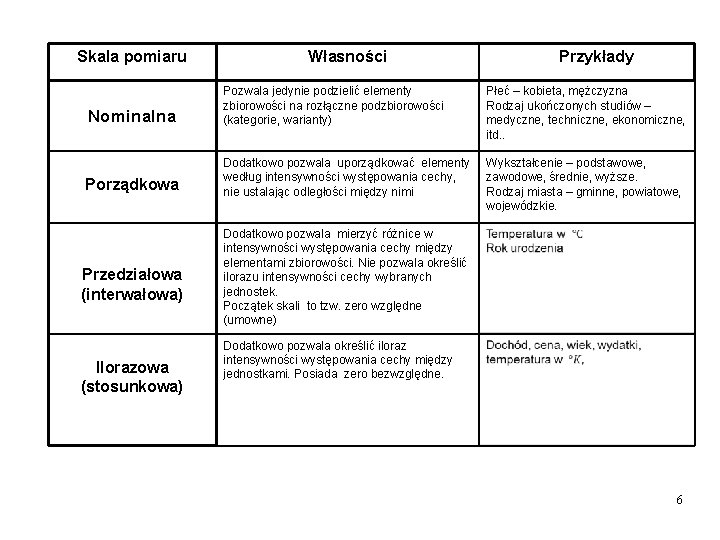
SKALE POMIAROWE Podstawą uznania cechy za mierzalną lub niemierzalną jest sposób jej pomiaru, czyli zastosowanie odpowiedniej skali pomiarowej. Jeżeli np. badaną cechą będzie wiek osób pewnej zbiorowości, to możemy wyrażać go liczbą ukończonych lat (czyli stosujemy tzw. skalę ilorazową) i cechę uznamy za mierzalną. Jeżeli interesuje nas tylko, czy osoby tej zbiorowości są młode, w wieku średnim, czy stare (stosujemy tzw. skalę porządkową), to cechę uznamy za niemierzalną. Skale pomiarowe stosowane w statystyce i ich własności przedstawia poniższa tabela. Skale są w niej uporządkowane od najsłabszej do najsilniejszej, tzn. , że każda z nich ma wszystkie własności skali poprzedniej oraz własności dodatkowe. 5

Skala pomiaru Własności Py. Przykłady Nominalna Pozwala jedynie podzielić elementy zbiorowości na rozłączne podzbiorowości (kategorie, warianty) Płeć – kobieta, mężczyzna Rodzaj ukończonych studiów – medyczne, techniczne, ekonomiczne, itd. . Porządkowa Dodatkowo pozwala uporządkować elementy według intensywności występowania cechy, nie ustalając odległości między nimi Wykształcenie – podstawowe, zawodowe, średnie, wyższe. Rodzaj miasta – gminne, powiatowe, wojewódzkie. Przedziałowa (interwałowa) Ilorazowa (stosunkowa) Dodatkowo pozwala mierzyć różnice w intensywności występowania cechy między elementami zbiorowości. Nie pozwala określić ilorazu intensywności cechy wybranych jednostek. Początek skali to tzw. zero względne (umowne) Dodatkowo pozwala określić iloraz intensywności występowania cechy między jednostkami. Posiada zero bezwzględne. 6

Przykład 1. 2. Wśród studentów AMW przeprowadzono ankietę, pytając o: wzrost, płeć, liczbę rodzeństwa Populacja – zbiór wszystkich studentów AMW. Jednostka statystyczna – student AMW. Cechy statystyczne – wzrost, płeć, liczba rodzeństwa. wzrost - cecha mierzalna ciągła, płeć - cecha niemierzalna, liczba rodzeństwa – cecha mierzalna skokowa. 7

2. Prezentacja rozkładu cechy statystycznej Rozkładem cechy statystycznej nazywamy uporządkowany zbiór par (xi, ni), gdzie xi oznacza wartości (kategorie, odmiany) cechy a ni liczbę jednostek statystycznych przyjmujących wartość xi. Rozkłady cech statystycznych można przedstawiać w postaci tabel, zwanych szeregami rozdzielczymi lub graficznie w postaci wykresów różnych typów. 8

9

W szeregu rozdzielczym liczebności można zastąpić częstościami względnymi wi= ni/n, z jakimi wartości cechy występują w rozkładzie. Wówczas szereg rozdzielczy punktowy ma postać: 10

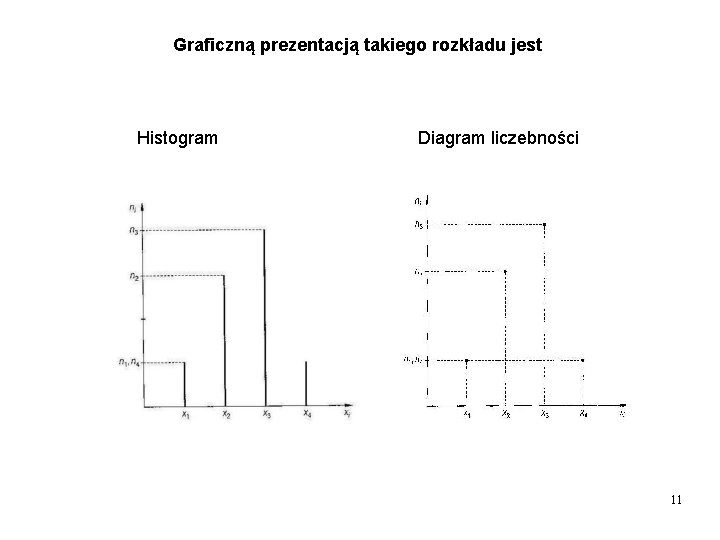
Graficzną prezentacją takiego rozkładu jest Histogram Diagram liczebności 11

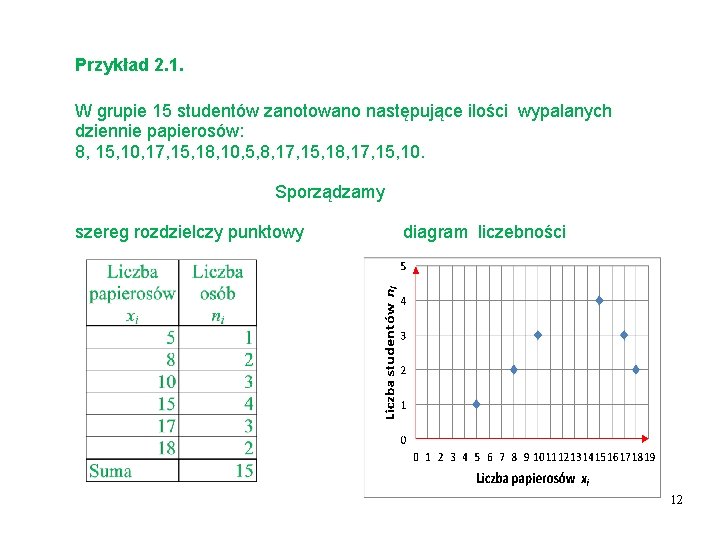
Przykład 2. 1. W grupie 15 studentów zanotowano następujące ilości wypalanych dziennie papierosów: 8, 15, 10, 17, 15, 18, 10, 5, 8, 17, 15, 10. Sporządzamy szereg rozdzielczy punktowy diagram liczebności 12

13

Przy budowie szeregu rozdzielczego przedziałowego będziemy kierowali się następującymi zasadami: - wyznaczone przedziały obejmują wszystkie wartości cechy występujące w populacji, - wyznaczone przedziały są rozłączne (żaden element nie może należeć do dwóch różnych klas, - w szeregu nie powinno być przedziałów pustych ( o zerowej liczbie jednostek), - przedziały mają tę samą rozpiętość (nie jest to wymóg konieczny ale wygodny w analizie statystycznej), - pierwszy przedział ma ustaloną dolną granicę a ostatni górną granicę (jeżeli pierwszy lub ostatni przedział jest nieograniczony, to sami ustalamy ograniczenia), - ustalamy rozstęp R=xmax – xmin między największą i najmniejszą wartością cechy, - ustalamy rozpiętość przedziałów h jako przybliżenie z nadmiarem liczby R/k, gdzie k oznacza liczbę utworzonych przedziałów (dokładność przybliżenia nie powinna być wyższa niż dokładność, z jaką podane są wartości badanej cechy), 14

Ustalanie liczby klas szeregu rozdzielczego przedziałowego 15

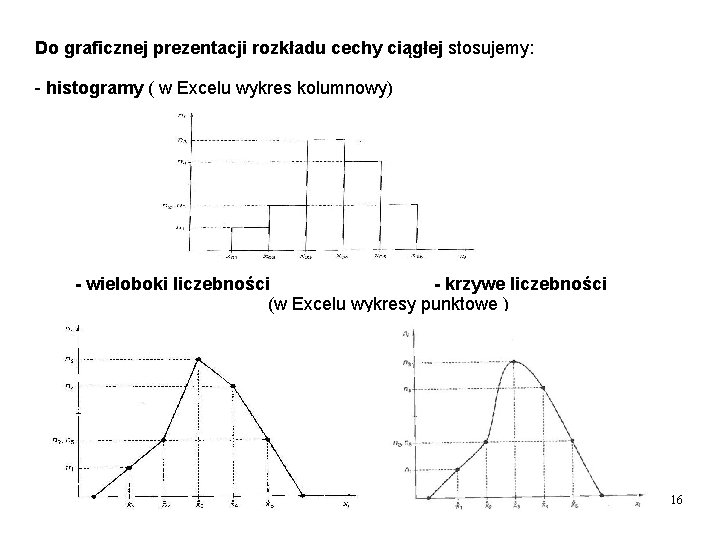
Do graficznej prezentacji rozkładu cechy ciągłej stosujemy: - histogramy ( w Excelu wykres kolumnowy) - wieloboki liczebności - krzywe liczebności (w Excelu wykresy punktowe ) 16

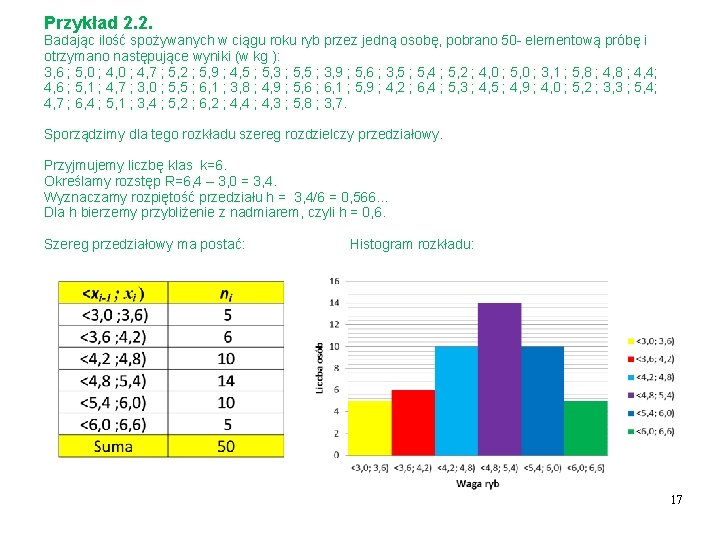
Przykład 2. 2. Badając ilość spożywanych w ciągu roku ryb przez jedną osobę, pobrano 50 - elementową próbę i otrzymano następujące wyniki (w kg ): 3, 6 ; 5, 0 ; 4, 7 ; 5, 2 ; 5, 9 ; 4, 5 ; 5, 3 ; 5, 5 ; 3, 9 ; 5, 6 ; 3, 5 ; 5, 4 ; 5, 2 ; 4, 0 ; 5, 0 ; 3, 1 ; 5, 8 ; 4, 4; 4, 6 ; 5, 1 ; 4, 7 ; 3, 0 ; 5, 5 ; 6, 1 ; 3, 8 ; 4, 9 ; 5, 6 ; 6, 1 ; 5, 9 ; 4, 2 ; 6, 4 ; 5, 3 ; 4, 5 ; 4, 9 ; 4, 0 ; 5, 2 ; 3, 3 ; 5, 4; 4, 7 ; 6, 4 ; 5, 1 ; 3, 4 ; 5, 2 ; 6, 2 ; 4, 4 ; 4, 3 ; 5, 8 ; 3, 7. Sporządzimy dla tego rozkładu szereg rozdzielczy przedziałowy. Przyjmujemy liczbę klas k=6. Określamy rozstęp R=6, 4 – 3, 0 = 3, 4. Wyznaczamy rozpiętość przedziału h = 3, 4/6 = 0, 566… Dla h bierzemy przybliżenie z nadmiarem, czyli h = 0, 6. Szereg przedziałowy ma postać: Histogram rozkładu: 17

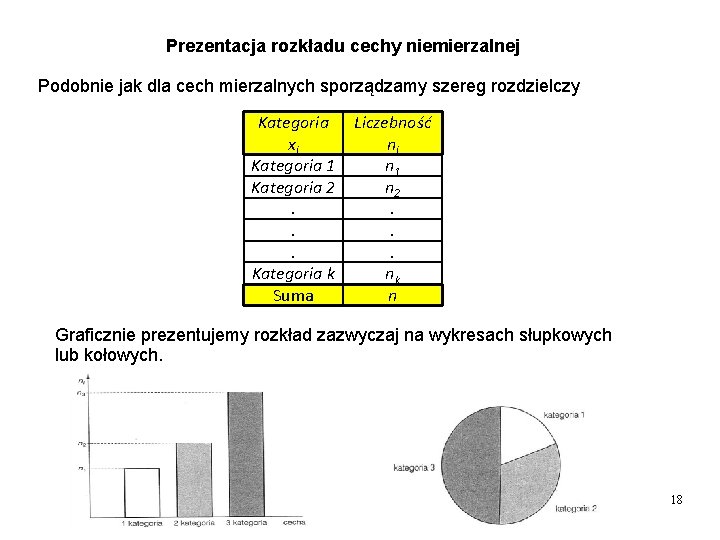
Prezentacja rozkładu cechy niemierzalnej Podobnie jak dla cech mierzalnych sporządzamy szereg rozdzielczy Kategoria xi Kategoria 1 Kategoria 2. . . Kategoria k Suma Liczebność ni n 1 n 2. . . nk n Graficznie prezentujemy rozkład zazwyczaj na wykresach słupkowych lub kołowych. 18

Przykład 2. 3. W sondzie ulicznej zapytano 20 osób, skąd głównie czerpią informacje o wydarzeniach w kraju i na świecie. Odpowiedzi były następujące: TVP, TVN, TVP, Polsat, TVP prasa, TVN, TVP, prasa, TVP, Polsat, TVN, TVP, Polsat, prasa, TVP. Prezentację rozkładu cechy „źródło informacji" podajemy w postaci szeregu rozdzielczego Źródło informacji Liczba osób TVP 8 TVN 5 Polsat 4 prasa 3 Razem 20 Liczba osób oraz wykresu słupkowego i kołowego prasa 15% 9 8 7 6 5 4 3 2 1 0 TVP TVN Polsat prasa TVP TVN Polsat Źródło informacji prasa TVP 40% Polsat 20% TVN 25% 19

3. Własności jednowymiarowych rozkładów cech statystycznych Rozkłady cech statystycznych analizuje się ze względu na cztery własności: położenie, dyspersję, , asymetrię, koncentrację. Położenie (przeciętny poziom) – to własność, która określa, w którym miejscu na osi liczbowej położone są wartości badanej cechy. Do oceny położenia rozkładu będziemy używali jednej z trzech wielkości: - średniej wartości cechy (średniej arytmetycznej), - wartości środkowej M(x) (mediany), - najczęściej występującej wartości D(x) (dominanty, mody). Rozkłady różniące się położeniem 20

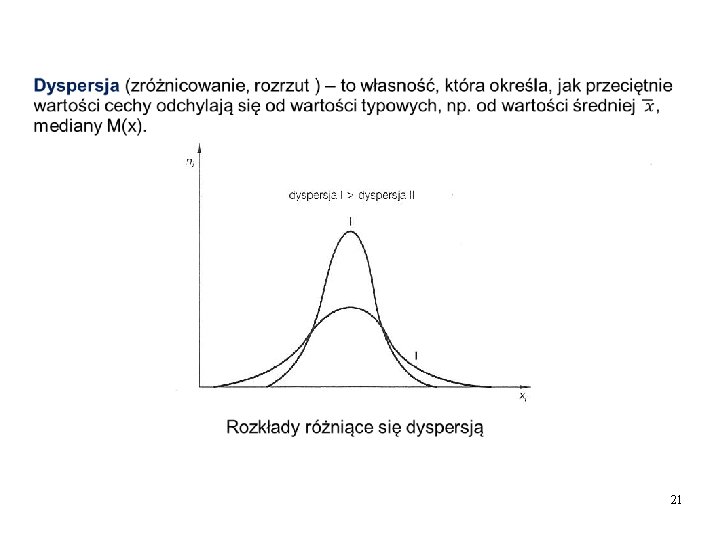
21

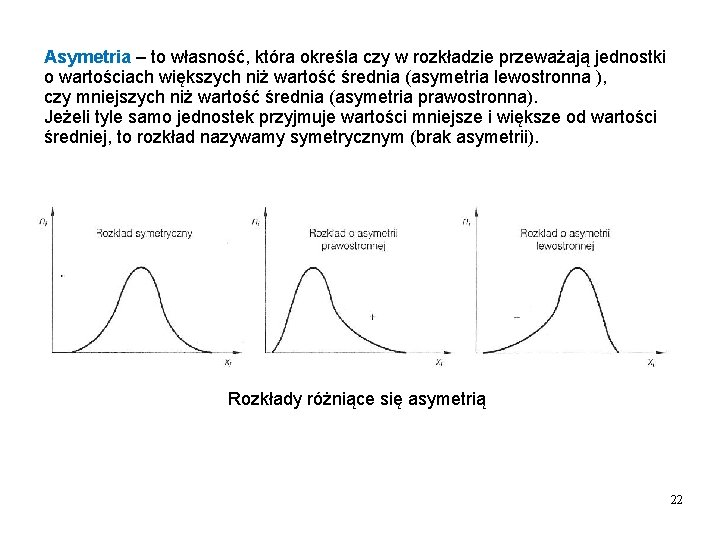
Asymetria – to własność, która określa czy w rozkładzie przeważają jednostki o wartościach większych niż wartość średnia (asymetria lewostronna ), czy mniejszych niż wartość średnia (asymetria prawostronna). Jeżeli tyle samo jednostek przyjmuje wartości mniejsze i większe od wartości średniej, to rozkład nazywamy symetrycznym (brak asymetrii). Rozkłady różniące się asymetrią 22

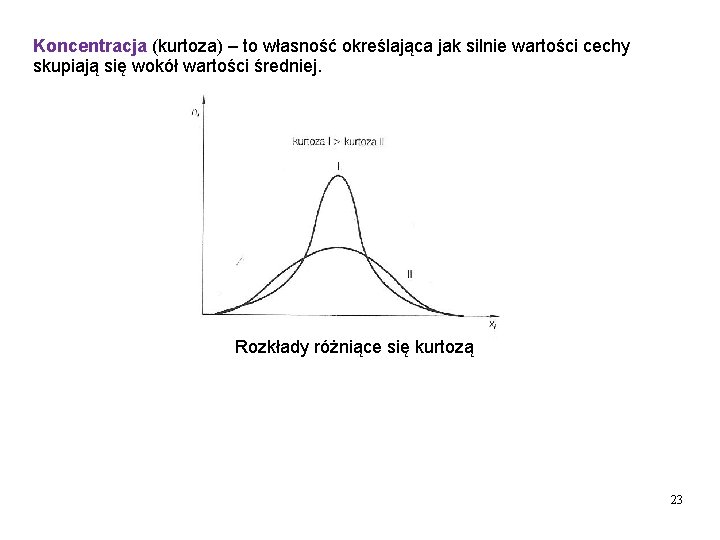
Koncentracja (kurtoza) – to własność określająca jak silnie wartości cechy skupiają się wokół wartości średniej. Rozkłady różniące się kurtozą 23

Typy rozkładów cech statystycznych Rozkłady typowe Wzorcem rozkładu typowego jest rozkład normalny (rozkład Gaussa) o wykresie: Rozkłady o umiarkowanej asymetrii, w których nie występują wartości znacznie odbiegające od przeciętnych, bardziej lub mniej spłaszczone zaliczamy do rozkładów typowych. Rozkłady typowe 24

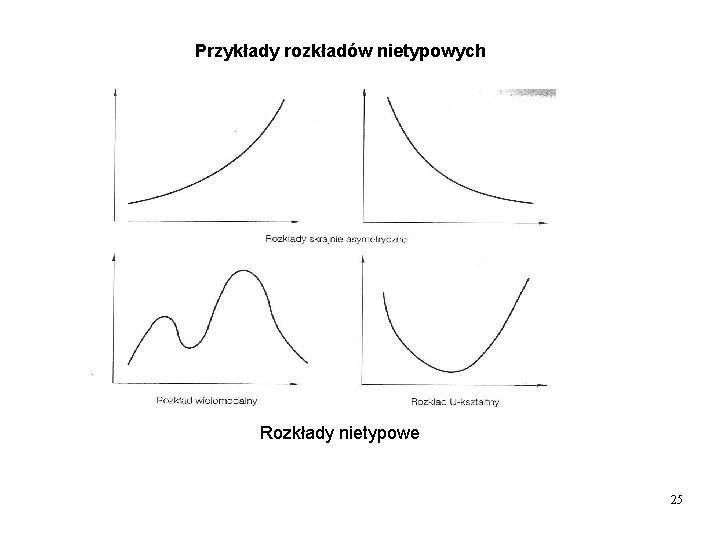
Przykłady rozkładów nietypowych Rozkłady nietypowe 25

4. Badanie własności rozkładów jednowymiarowych Miary położenia: - miary klasyczne - średnia arytmetyczna - miary pozycyjne - dominanta D(x) - mediana M(x) - kwartyle Qk(x) Miary dyspersji: - miary klasyczne - wariancja s 2(x) - odchylenie standardowe s(x) - klasyczny współczynnik zmienności V(x) - miary pozycyjne - odchylenie ćwiartkowe Q(x) - pozycyjny współczynnik zmienności Vp(x) 26

Miary asymetrii: - klasyczny współczynnik asymetrii A(x) - pozycyjny współczynnik asymetrii Ap(x) Miary koncentracji: - współczynnik koncentracji K(x) - współczynnik ekscesu g(x) Miary klasyczne stosujemy w rozkładach typowych. Miary pozycyjne można stosować w rozkładach dowolnych. 27

Średnia arytmetyczna Dla szeregu rozdzielczego punktowego gdzie: - wartości cechy dla i=1, 2, 3, …, k - liczba jednostek przyjmujących wartość dla i=1, 2, 3, …, k, Dla szeregu rozdzielczego przedziałowego gdzie: - środek przedziału <xi-1 ; xi) dla i=1, 2, 3, …, k. Interpretacja: gdyby wszystkie jednostki zbiorowości miały taką samą wartość, to byłaby ona 28 równa średniej arytmetycznej

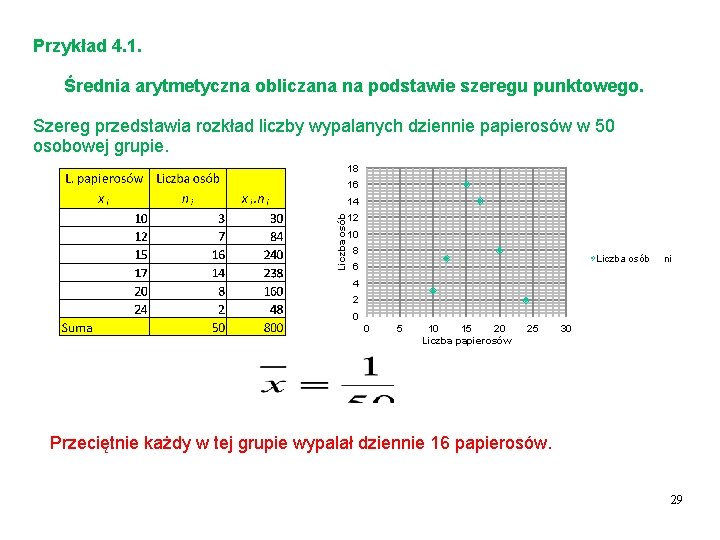
Przykład 4. 1. Średnia arytmetyczna obliczana na podstawie szeregu punktowego. Szereg przedstawia rozkład liczby wypalanych dziennie papierosów w 50 osobowej grupie. 18 16 Liczba osób 14 12 10 8 Liczba osób ni 6 4 2 0 0 5 10 15 20 Liczba papierosów 25 30 Przeciętnie każdy w tej grupie wypalał dziennie 16 papierosów. 29

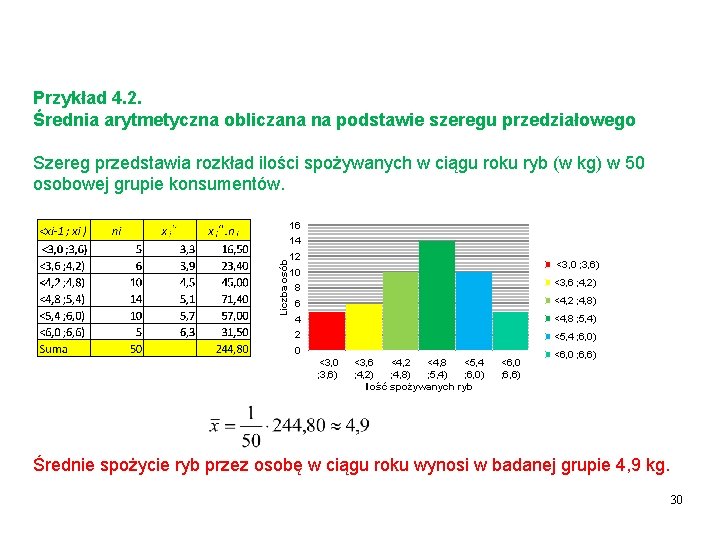
Przykład 4. 2. Średnia arytmetyczna obliczana na podstawie szeregu przedziałowego Szereg przedstawia rozkład ilości spożywanych w ciągu roku ryb (w kg) w 50 osobowej grupie konsumentów. 16 Liczba osób 14 12 <3, 0 ; 3, 6) 10 8 <3, 6 ; 4, 2) 6 <4, 2 ; 4, 8) 4 <4, 8 ; 5, 4) 2 <5, 4 ; 6, 0) 0 <3, 0 ; 3, 6) <3, 6 <4, 2 <4, 8 <5, 4 ; 4, 2) ; 4, 8) ; 5, 4) ; 6, 0) Ilość spożywanych ryb <6, 0 ; 6, 6) Średnie spożycie ryb przez osobę w ciągu roku wynosi w badanej grupie 4, 9 kg. 30

Mediana (wartość środkowa) Mediana to taka liczba, która dzieli zbiorowość na dwie części: połowa jednostek przyjmuje wartości mniejsze lub równe, natomiast druga połowa wartości większe lub równe medianie. Graficzna interpretacja mediany 31

Sposób wyznaczania mediany na podstawie szeregu punktowego - wartości cechy w szeregu porządkujemy rosnąco - wyznaczamy pozycję mediany p=n/2, czyli jednostki środkowej - jeżeli p nie jest liczbą całkowitą, to medianą jest jednostka o numerze (n+1)/2, czyli - jeżeli p jest liczbą całkowitą , to: - dla cechy ciągłej i quasi-ciągłej - dla cechy skokowej wyznaczamy dwie mediany 32

Sposób wyznaczania mediany na podstawie szeregu przedziałowego - wyznaczamy pozycję mediany p=n/2 - wskazujemy przedział mediany, czyli przedział, w którym leży jednostka o numerze [p]+1 - przybliżoną wartość mediany obliczamy z wzoru gdzie: - początek przedziału mediany - rozpiętość przedziału mediany - liczebność przedziału mediany - suma liczebności przedziałów poprzedzających przedział mediany. 33

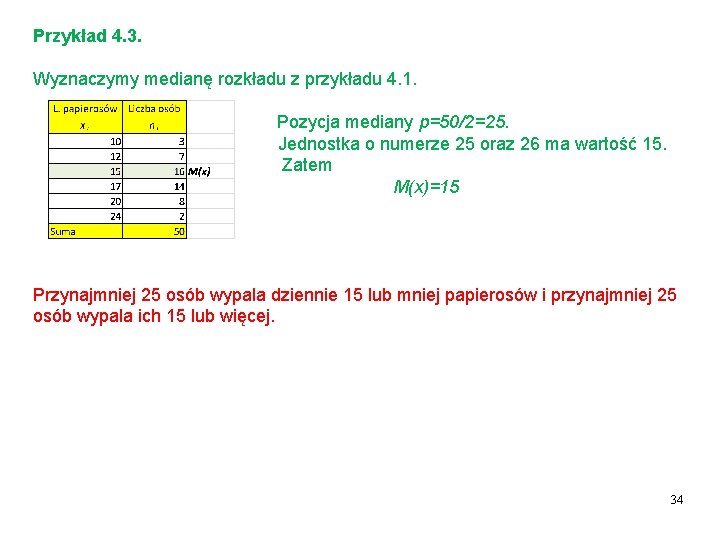
Przykład 4. 3. Wyznaczymy medianę rozkładu z przykładu 4. 1. Pozycja mediany p=50/2=25. Jednostka o numerze 25 oraz 26 ma wartość 15. Zatem M(x)=15 Przynajmniej 25 osób wypala dziennie 15 lub mniej papierosów i przynajmniej 25 osób wypala ich 15 lub więcej. 34

Przykład 4. 4. Wyznaczymy medianę z przykładu 4. 2. Pozycja mediany p=50/2=25. Jednostka o numerze 25 oraz 26 leży w przedziale <4, 8 ; 5, 4), więc jest to przedział mediany. 25 osób spożywa rocznie co najwyżej 5 kg ryb i 25 osób co najmniej 5 kg. 35

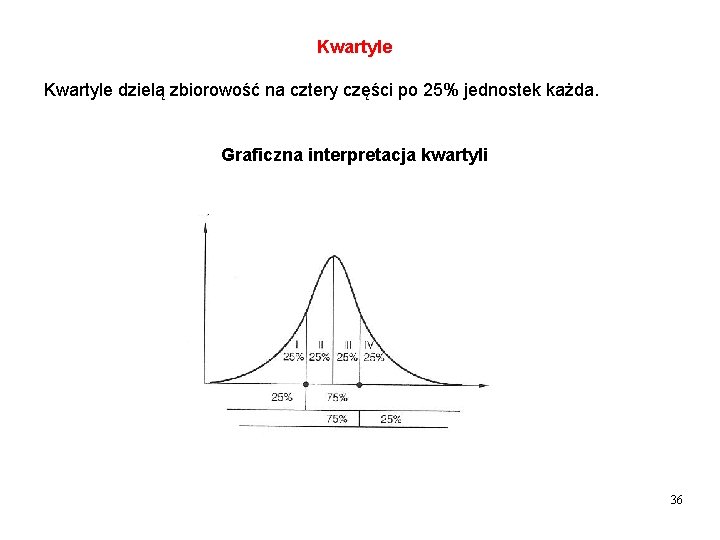
Kwartyle dzielą zbiorowość na cztery części po 25% jednostek każda. Graficzna interpretacja kwartyli 36

Sposób wyznaczania kwartyli na podstawie szeregu punktowego - wartości cechy w szeregu porządkujemy rosnąco - wyznaczamy pozycję kwartyla pk=k∙n/4 - jeżeli pk nie jest liczbą całkowitą, to kwartyl Qk(x) przyjmuje taką wartość, jak jednostka o numerze następnym za pozycją kwartyla - jeżeli pk jest liczbą całkowitą , to: - dla cechy ciągłej i quasi-ciągłej - dla cechy skokowej wyznaczamy dwa kwartyle 37

Sposób wyznaczania kwartyli na podstawie szeregu przedziałowego - wyznaczamy pozycję mediany pk=k∙n/4 - wskazujemy przedział kwartyla, czyli przedział, w którym leży jednostka o numerze [pk]+1 - przybliżoną wartość kwartyla obliczamy z wzoru gdzie: - początek przedziału kwartyla - rozpiętość przedziału kwartyla - liczebność przedziału kwartyla - suma liczebności przedziałów poprzedzających przedział kwartyla 38

Przykład 4. 5. Wyznaczanie kwartyli na podstawie szeregu punktowego Wyznaczymy kwartyle z przykładu 4. 1. Wyznaczamy pozycje kwartyli: p 1=1∙ 50/4=12, 5 L. papierosów Liczba osób xi ni p 2=2∙ 50/4=25 10 3 p 3=3∙ 50/4=37, 5 12 7 15 16 Q 1, Q 2 Stąd: 17 14 Q 3 20 8 Q 1(x)=x 13=15 24 2 Q 2(x)=x 25=15 - mediana Suma 50 Q 3(x)=x 38=17 Przynajmniej 25% palaczy wypala 15 papierosów lub mniej, przynajmniej 25% palaczy wypala 17 lub więcej papierosów. 39

Przykład 4. 6. Wyznaczanie kwartyli na podstawie szeregu przedziałowego Wyznaczymy kwartyle rozkładu z przykładu 4. 2. Wyznaczamy pozycje kwartyla pierwszego i trzeciego (kwartyl drugi, czyli medianę już wyznaczaliśmy): p 1=1∙ 50/4=12, 5 p 3=3∙ 50/4=37, 5 Wynika stąd, że kwartyle leżą w przedziałach zaznaczonych w tabeli. 25% badanych spożywa rocznie co najwyżej 4, 3 kg ryb i 25% badanych spożywa ich co najmniej 5, 6 kg. 40

Dominanta (moda) Dominanta D(x) jest to wartość cechy najczęściej występująca w zbiorowości (najwięcej jednostek przyjmuje wartość D(x) ). Wyznaczanie dominanty ma sens dla rozkładów typowych oraz nietypowych wielomodalnych. Wyznaczanie dominanty na podstawie szeregu punktowego polega na wskazaniu wartości cechy występującej w rozkładzie najczęściej. Dla szeregu przedziałowego dominantę wyznaczamy z wzoru przybliżonego: gdzie: - początek przedziału dominanty - liczebność przedziału dominanty -odpowiednio liczebność przedziału poprzedzającego przedział dominanty i następującego po nim. - rozpiętość przedziału dominanty 41

Przykład 4. 7. Wyznaczanie dominanty na podstawie szeregu przedziałowego Wyznaczymy dominantę rozkładu z przykładu 4. 2. Najczęściej występująca ilość spożywanych ryb przez jedną osobę w ciągu roku to 5, 1 kg. 42

Klasyczne miary dyspersji Wariancja s 2(x) to średnia arytmetyczna kwadratów odchyleń wartości cechy od wartości średniej. Jeżeli wariancja jest równa 0, to znaczy, że wszystkie jednostki zbiorowości miały tę samą wartość. Dla szeregu rozdzielczego punktowego wariancję obliczamy z wzoru: Dla szeregu rozdzielczego przedziałowego z wzoru: Odchylenie standardowe s(x) 43

44

Pozycyjne miary dyspersji Odchylenie ćwiartkowe Q(x) – ocenia zróżnicowanie wartości dla 50% środkowych jednostek (między kwartylem trzecim a pierwszym). Pozycyjny współczynnik zmienności Vp(x) Pozycyjny współczynnik zmienności ocenia siłę dyspersji, którą interpretujemy tak samo jak w przypadku współczynnika klasycznego. Uwaga: Klasyczny współczynnik zmienności jest dokładniejszą miarą dyspersji niż współczynnik pozycyjny, ponieważ uwzględnia wszystkie wartości cechy (współczynnik pozycyjny tylko 50%). Klasyczny współczynnik zmienności stosujemy w ocenie dyspersji tylko rozkładów typowych, pozycyjny zaś w dowolnych rozkładach. 45

Przykład 4. 7. Wyznaczymy miary dyspersji dla rozkładu z przykładu 4. 1. Zarówno klasyczny jak i pozycyjny współczynnik zmienności wskazują, że dyspersja rozkładu jest słaba, tzn. , że badana grupa jest mało zróżnicowana pod względem liczby wypalanych papierosów. 46

Przykład 4. 8. Wyznaczymy miary dyspersji dla rozkładu z przykładu 4. 2. Zarówno klasyczny jak i pozycyjny współczynnik zmienności wskazują, że dyspersja rozkładu jest słaba, tzn. , że badana grupa jest mało zróżnicowana pod względem ilości spożywanych ryb w ciągu roku. 47

Miary asymetrii Jeżeli liczba jednostek o wartościach mniejszych i większych od wartości średniej jest taka sama, to rozkład jest symetryczny. Asymetria prawostronna (dodatnia) ma miejsce wtedy, gdy w rozkładzie przeważają jednostki o wartościach mniejszych od wartości średniej. Asymetrię lewostronną (ujemną) wykazuje rozkład, w którym więcej jest jednostek o wartościach większych od wartości średniej. Miarą siły asymetrii jest klasyczny współczynnik asymetrii: gdzie: dla szeregu rozdzielczego punktowego oraz dla szeregu rozdzielczego przedziałowego 48

Miary asymetrii Bezwzględna wartość współczynnika asymetrii zazwyczaj nie przekracza wartości 2. Mówimy, że asymetria rozkładu jest: - słaba, jeżeli - umiarkowana, jeżeli - silna, jeżeli Klasyczny współczynnik asymetrii stosujemy tylko do oceny siły asymetrii rozkładów typowych. 49

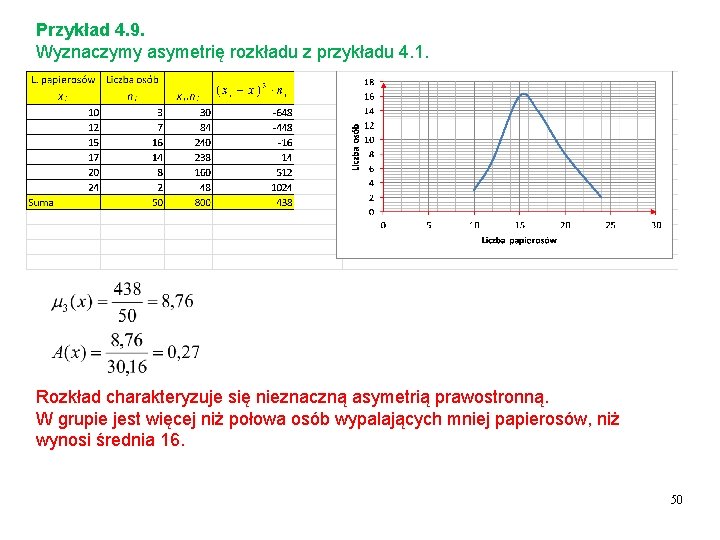
Przykład 4. 9. Wyznaczymy asymetrię rozkładu z przykładu 4. 1. Rozkład charakteryzuje się nieznaczną asymetrią prawostronną. W grupie jest więcej niż połowa osób wypalających mniej papierosów, niż wynosi średnia 16. 50

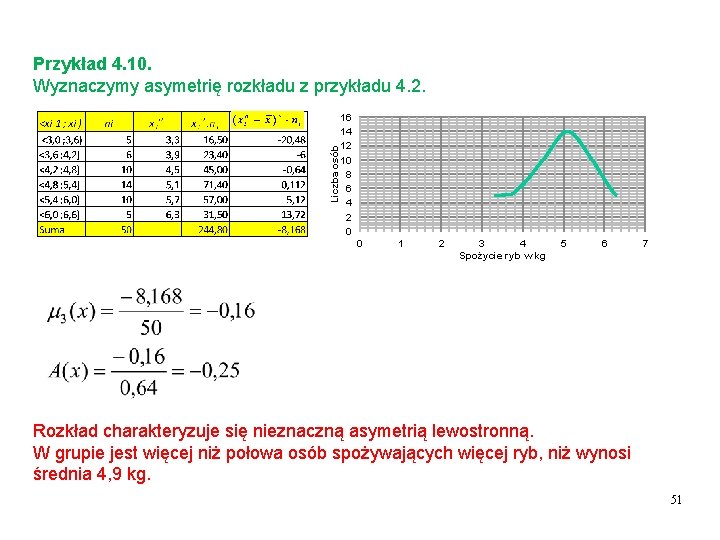
Liczba osób Przykład 4. 10. Wyznaczymy asymetrię rozkładu z przykładu 4. 2. 16 14 12 10 8 6 4 2 0 0 1 2 3 4 Spożycie ryb w kg 5 6 7 Rozkład charakteryzuje się nieznaczną asymetrią lewostronną. W grupie jest więcej niż połowa osób spożywających więcej ryb, niż wynosi średnia 4, 9 kg. 51

Miary koncentracji (kurtozy) Kurtoza to stopień skupienia wartości cechy wokół wartości średniej. Oceny kurtozy dokonujemy tylko dla rozkładów typowych symetrycznych lub o nieznacznej asymetrii. Miarą kurtozy jest współczynnik koncentracji gdzie dla szeregów rozdzielczych punktowych dla szeregów rozdzielczych przedziałowych Przy ocenie kurtozy za wzorzec przyjmujemy rozkład normalny standardowy, dla którego K(x)=3. 52

Miary koncentracji Różnica zwana współczynnikiem ekscesu, wskazuje, czy skupienie jednostek wokół wartości średniej jest silniejsze, czy słabsze niż w rozkładzie normalnym standardowym. Jeżeli =0, to stopień skupienia jest taki sam, jak w rozkładzie normalnym standardowym. Jeżeli <0, to wykres rozkładu jest bardziej spłaszczony niż rozkładu normalnego standardowego. Jeżeli >0, to wykres jest bardziej wysmukły. 53

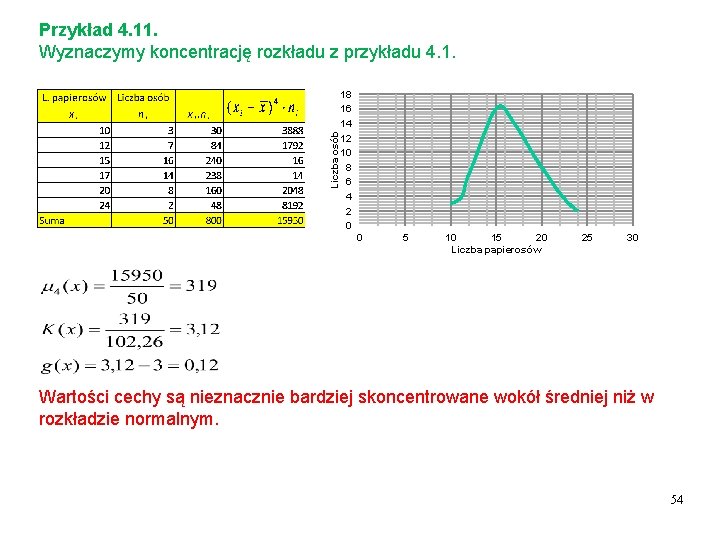
Liczba osób Przykład 4. 11. Wyznaczymy koncentrację rozkładu z przykładu 4. 1. 18 16 14 12 10 8 6 4 2 0 0 5 10 15 20 Liczba papierosów 25 30 Wartości cechy są nieznacznie bardziej skoncentrowane wokół średniej niż w rozkładzie normalnym. 54

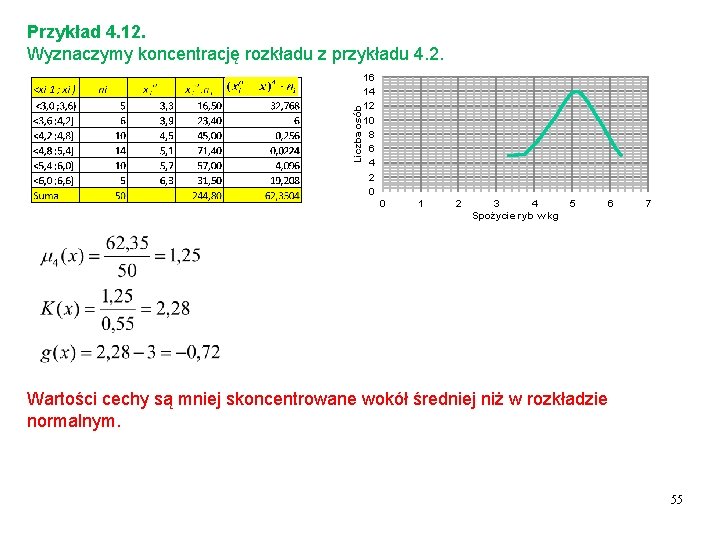
Liczba osób Przykład 4. 12. Wyznaczymy koncentrację rozkładu z przykładu 4. 2. 16 14 12 10 8 6 4 2 0 0 1 2 3 4 Spożycie ryb w kg 5 6 7 Wartości cechy są mniej skoncentrowane wokół średniej niż w rozkładzie normalnym. 55

56

57

Krzywa Lorenza Porównując położenie krzywej Lorenza względem linii równomiernego podziału, oceniamy siłę koncentracji: - jeżeli krzywa Lorenza pokrywa się z linią równomiernego podziału, oznacza to brak koncentracji, czyli każda jednostka zbiorowości dysponuje taką samą częścią ogólnej sumy wartości; jest to sytuacja skrajna, oznacza również brak dyspersji (np. każde gospodarstwo rolne ma taką samą część ogólnego areału użytków rolnych); - jeżeli krzywa Lorenza odchyla się od linii równomiernego podziału znaczy to, że występuje koncentracja, tym silniejsza im odchylenie jest większe (im większe jest pole a ); - jeżeli krzywa Lorenza przebiega wzdłuż boków kwadratu AB i BC (pole a jest równe polu trójkąta ABC), oznacza to koncentrację zupełną. Sytuacja taka zachodzi wtedy, gdy jedna jednostka dysponuje całą sumą wartości (np. jedno gospodarstwo rolne dysponuje całym areałem użytków rolnych). 58

59

60

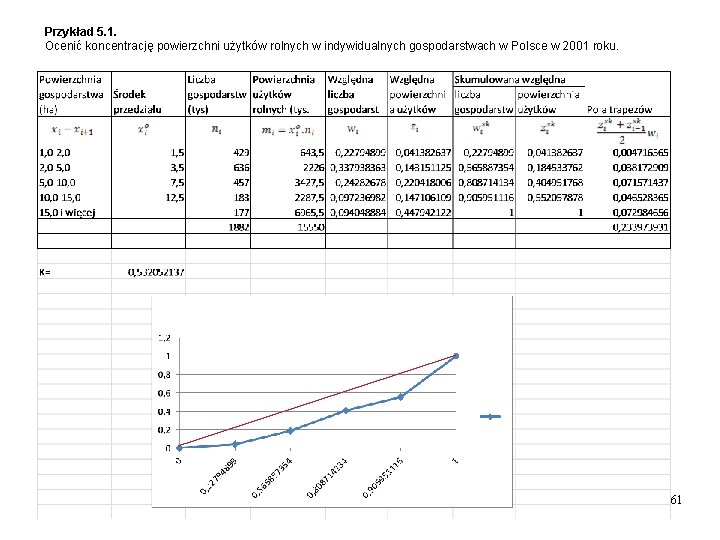
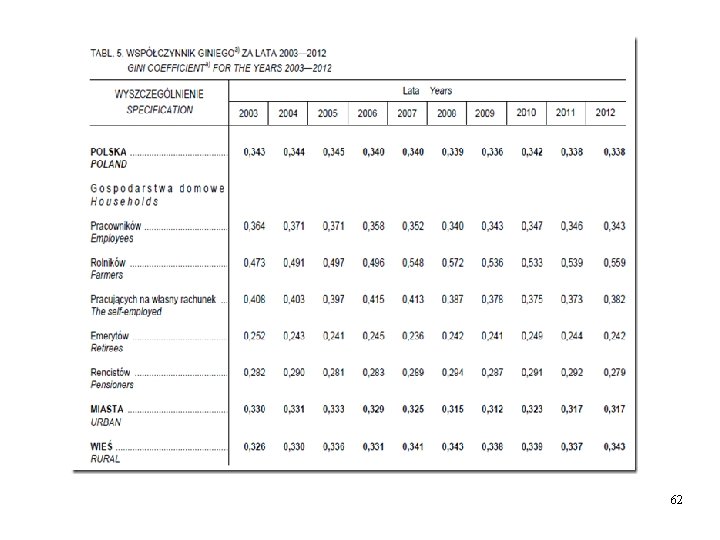
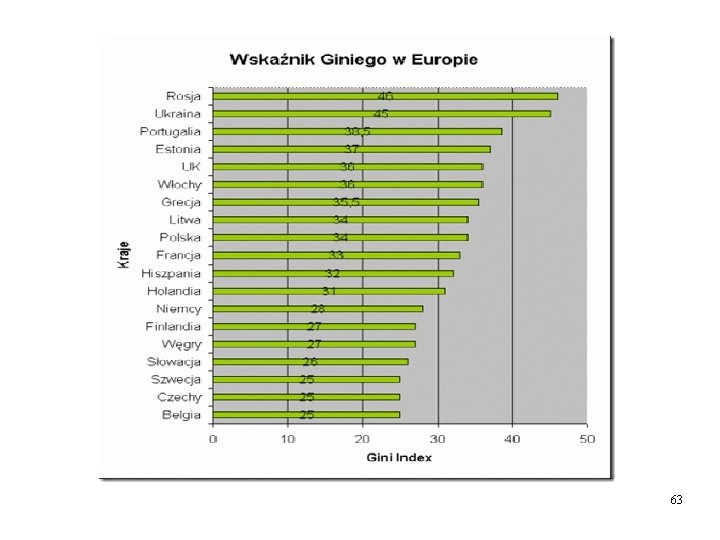
Przykład 5. 1. Ocenić koncentrację powierzchni użytków rolnych w indywidualnych gospodarstwach w Polsce w 2001 roku. 61

62

63

64

65

66

67

68

Prezentacja przygotowana na podstawie pozycji: Maksimowicz-Ajchel A. , Wstęp do statystyki, Wydawnictwo Uniwersytetu Warszawskiego, Warszawa 2007. King B. M. , Minium E. W. , Statystyka dla psychologów i pedagogów, Wydawnictwo Naukowe PWN, Warszawa 2009. 69