Stats 95 Normal Distributions Normal Distribution Probability Events

Stats 95

Normal Distributions

Normal Distribution & Probability • Events that will fall in the shape of a Normal distribution: – Measures of weight, height, IQ etc… – Measurement errors of weight, height, IQ etc… – Probability of coin tosses, dice and other (repeated) random events

Probability Distribution: Spreading the Luck Around • "If a fair coin is flipped 100 times, what is the probability of getting 60 or more heads? “ • Abraham de Moivre, an 18 th century statistician and consultant to gamblers was often called upon to make these lengthy computations. de Moivre noted that when the number of events (coin flips) increased, the shape of the binomial distribution approached a very smooth curve.

Outcome 1 2 3 4 First Flip Heads Tails Outcomes Second Flip Heads Tails

Probability Distribution A probability distribution is an expression of the anatomy of chance. It does the impossible, expressing in numbers the likelihood of something we cannot predict. In the coin toss example, the probability distribution can tell us what percentage of 12 coin tosses will have 1 T, 2 T, 3 T, 4 T… 12 T. You express the probability in percentiles (e. g. , 50 th percentile = probability of. 5) using z-scores (e. g. , z-score 0 = 50 th percentile).


How To Calculate Standard Deviation Friends on Facebook X X-μ (X-μ)^2 124 -236. 75 56050. 56 191 -169. 75 28815. 06 171 957 -189. 75 596. 25 36005. 06 355514. 1 360. 75 = 476384. 8 = 119096. 2 = 345. 1032

Z-Scores: The Standard Deviation “Meter” • Use Z-scores to express values regardless of the original unit of measure • E. g. , feet or meters • Once you have the standard deviation, you can go from raw scores to z-scores, and from zscores to raw scores.

How To Calculate Z-scores Friends on Facebook X X-μ (X-μ)^2 124 -236. 75 56050. 56 191 -169. 75 28815. 06 171 957 -189. 75 596. 25 36005. 06 355514. 1 = 360. 75 476384. 8 119096. 2 345. 1032

How To Calculate Z-scores Friends on Facebook X X-μ (X-μ)^2 124 -236. 75 56050. 56 191 -169. 75 28815. 06 171 957 -189. 75 596. 25 36005. 06 355514. 1 Z-score -0. 68603 -0. 49188 -0. 54984 1. 727744 = 360. 75 476384. 8 119096. 2 345. 1032

Z-Scores & Percentiles • Each z-score is associated with a percentile. – Z-scores tell us the percentile of a particular score – Can tell us % of pop. above or below a score, and the % of pop. between the score and the mean and the tail.

Transforming Zscore into Percentiles a) DRAW A GRAPH! b) Calculate z-score c) Estimate the percentile of the zscore using probability distribution d) Use z-score chart to transform z-score into percentile e) Use graph to make sure answer makes sense • Draw a Graph!…did I mention you need to draw a graph? Yeah, draw a graph.

Transforming z. Scores into Percentiles • Use a chart like this in Appendix A of your text (Yes, you need the textbook) to find the percentile of you z-score. • This table gives the distance between the mean (zero) and the z-score. • To calculate cumulative percentile : • Of positive z-score 50 + (z) • Of negative z-score 50+ (-z)
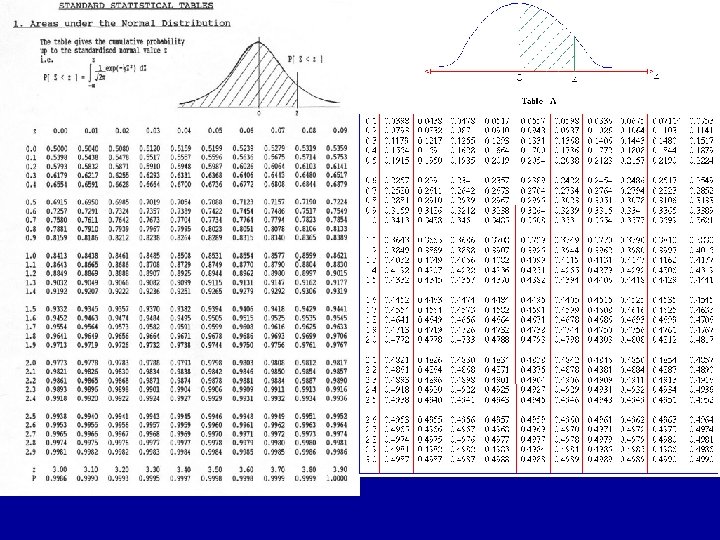

Example: Height • Jessica has a height of 66. 41 inches tall (5’ 6’’) • The mean of the population of height for girls is 63. 80 • The standard deviation for the population height fir girls is 2. 66 • According to z-score table, the percentile associated with z =. 98 is 33. 65%

Height Example: Did I mention? DRAW A GRAPH!! • Jessica’s z-score for height is. 98, associated percentage of 33. 65%. • This means – there is 33. 65% of the population is between the mean and Jessica’s score. – There is a 33. 65% chance of Jess being taller than the average by this amount BY CHANCE ALONE • Mean = 50 th percentile, therefore to find the Jessica’s percentile = 33. 65+50 = 83. 65%. • 84% of the population of girls is shorter than Jessica, and there is a 100 -84% = 16% chance of someone being this tall by CHANCE ALONE.

Central Limit Theorem • The central limit theorem states that IF you take an: a. b. c. infinite number of successive random samples from ANY SHAPED population • THEN the distribution of sample means calculated for each sample will become approximately normally distributed a) becoming more accurate the larger the size of each sample b) with mean μ and standard deviation σ / √ N William Sealy Gosset
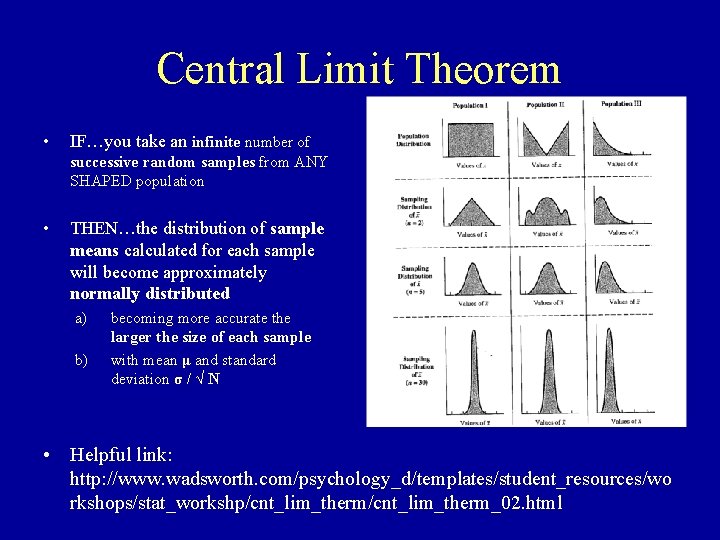
Central Limit Theorem • IF…you take an infinite number of successive random samples from ANY SHAPED population • THEN…the distribution of sample means calculated for each sample will become approximately normally distributed a) b) becoming more accurate the larger the size of each sample with mean μ and standard deviation σ / √ N • Helpful link: http: //www. wadsworth. com/psychology_d/templates/student_resources/wo rkshops/stat_workshp/cnt_lim_therm_02. html

Distributions of the Guess from the Survey Distribution of “Guess a # 1 -100 Distribution of “Guess the class mean of guesses 1 -100”

Distribution of Means and Sample Size As the sample size of each sample in the distribution of means increases, the normal curve becomes narrower and taller (more normal)

Normal Distribution v. Distribution of Means • Normal Distribution: distribution of raw scores – E. g. , roll a die 100 times and plot the frequency of • Distribution of means: distribution of the averages of randomly chosen samples (size N) from a distribution of raw scores. – E. g. , roll a die 100 times and take the average for every four randomly selected sample with replacement 25 times, and plot the average.

Distribution of Sample Means: Central Limit Theorem in Action Rectangular distribution of random variables from the roll of a die. Distribution of the sample means from the rectangular distribution on the left. According to the Central Limit Theorem, the distribution becomes normal, the standard deviation smaller.

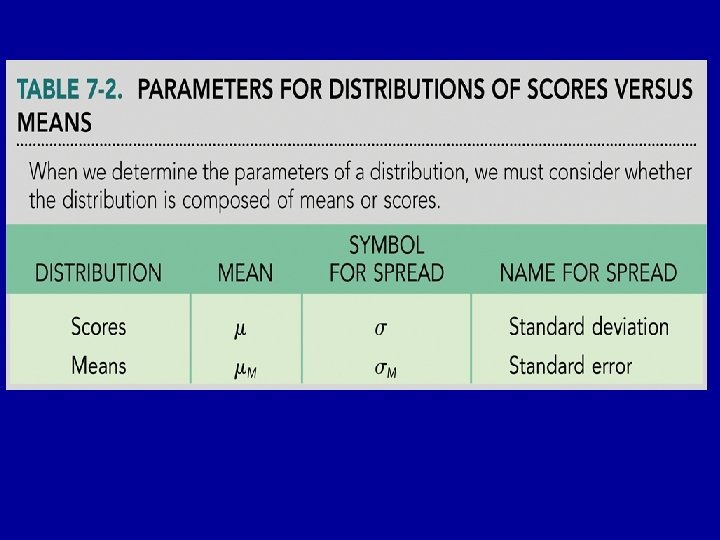
Normal Distribution v. Distribution of Means • Normal Distributions standard deviation & z-scores • Distribution of means standard deviation & z-scores

Normal Distribution v. Distribution of Means • Distribution of means standard deviation & z-scores • = Standard Error • N = The sample size of each mean sample. NOT the number of mean samples in the distribution, and NOT the size of the population of individual scores, e. g. , three girls, not 10 groups of three girls, not the 120 girls in the population. M = the mean height of the three girls The mean of the distribution of the sample means will equal the mean of the population of raw scores

Sample Mean Example: Height • Jessica, Joni and Barbi have an average height of 66. 41 inches tall (5’ 6’’) • The mean of the population of height for girls is 63. 80 • The standard deviation for the population height for girls is 2. 66 • According to z-score table, the percentile associated with z = 1. 699 is 45. 54%

Compare Z-score of Single Sample and Sample Mean Z-score individual score Z-score of sample mean • Scenario: Jessica has a height of 66. 41 inches tall (5’ 6’’). The mean of the population of height for girls is 63. 80. The standard deviation for the population height for girls is 2. 66. What is Jess’ z-score? • Scenario: Jessica, Joni and Barbi have an average height of 66. 41 inches tall (5’ 6’’). The mean of the population of height for girls is 63. 80. The standard deviation for the population height for girls is 2. 66. What is the z-score for mean of the sample size of three (N = 3) girls?

Compare Z-score of Single Sample and Sample Mean Z-score individual score Z-score of sample mean • N=1 • Jessica height =66. 41 • N=3 • average height = 66. 41 • μ = 63. 80. • SD or σ = 2. 66 • What is Jess’ z-score? • SD or σ = 2. 66 • Standard Error = • What is the z-score for mean of the sample size of three (N = 3) girls?


- Slides: 31