STATISTIQUES APPLIQUEES POUR LA PRODUCTIQUE PLAN DU COURS

STATISTIQUES APPLIQUEES POUR LA PRODUCTIQUE

PLAN DU COURS I. III. IV. V. VII. Introduction Analyse descriptive des données Paramètres statistiques Introduction au calcul des probabilités Lois de probabilité, Exemples Echantillonnage, estimation, décision Cartes de contrôle, capabilité d’un procédé

PLAN DU COURS

I. Introduction

I. Introduction QU’EST-CE QUE LA QUALITE ? • Pour réussir dans le climat économique du XXI ème siècle, une entreprise doit fournir des produits satisfaisant aux exigences de la clientèle. • Un produit (bien ou service) est le résultat d’un processus. • Un produit de qualité est un produit qui satisfait aux exigences du client. • La qualité d’un produit peut être décrite par des caractéristiques intrinsèques appelées caractéristiques de qualité. • On peut exploiter dans ce but des caractéristiques mesurables ou des attributs.

I. Introduction VARIABILITE • Tout processus de production comporte des facteurs techniques, administratifs et humains qui concourent à la réalisation du produit. • Les éléments qui interviennent dans un processus ne restent pas parfaitement constants dans le temps. Ils varient et leurs influences se répercutent par la suite dans la production. • Pour toutes les entreprises, la variabilité des caractéristiques de qualité constitue un obstacle majeur pour fournir des produits qui répondent aux exigences des clients.

I. Introduction POURQUOI CE COURS ? • Donner les méthodes pour l’assurance et l’amélioration continue de la qualité • Il s’agit de techniques concrètes qui peuvent être utilisées pour améliorer les performances de n’importe quel processus (industriel ou administratif) présentant des variations

I. Introduction APPROCHE HISTORIQUE • Les méthodes de base pour l’assurance qualité datent des années 1920 -1930 • Première période: la demande est supérieure à l’offre jusqu’en 1975. Il suffisait de produire pour vendre. Mise en œuvre de verrous de contrôle pour garantir la livraison de produits conformes (stratégie de détection). Il y a du gaspillage mais les profits le permettaient. • Deuxième période: après le premier choc pétrolier, la concurrence s’est intensifiée et les exigences des clients n’ont cessé de croître d’où la nécessité de produire de la bonne qualité du premier coup et au juste coût.

I. Introduction MAITRISE STATISTIQUE DES PROCEDES MSP Il est évidemment plus économique de produire un produit ayant « zéro défaut » que de trier les unités nonconformes. Ainsi le monde industriel a évolué vers une stratégie de prévention. Il s’est attaché à produire du « zéro défaut » en utilisant des techniques scientifiques telles que les méthodes de la maîtrise statistique des procédés.

I. Introduction MSP - PRINCIPE Recueillir des informations sur le produit et/ou son processus de fabrication et exploiter ces informations pour agir efficacement sur le processus: - pour réduire, éliminer et prévenir les non conformités en matière de qualité. - pour améliorer de façon continue les performances.

I. Introduction MSP – MISE EN OEUVRE Afin que ces techniques soient efficaces et que l’entreprise soit à la hauteur des défis, elle doit mettre en place un système de management visant à maîtriser tous les facteurs ayant une incidence sur la qualité. Il ne sera jamais possible de créer des produits ou des caractéristiques exactement identiques (exemples: les diamètres d’un piston, le poids des pâles d’hélicoptère, le poids des comprimés d’un médicament etc…) varient d’une unité à l’autre. Pour prospérer dans le climat économique d’aujourd’hui, il convient d’améliorer constamment la qualité afin de satisfaire pleinement la clientèle et éviter les surcoûts. La variabilité des processus pose donc problème.

I. Introduction MSP – AMELIORATION DE LA QUALITE La clef pour l’amélioration de la qualité consiste donc à réduire la variabilité du processus de production. Il est impossible d’améliorer la qualité sans connaître la variabilité, il est impossible de connaître la variabilité sans utiliser de METHODES STATISTIQUES.

II. Analyse descriptive des données

II. Analyse descriptive des données OBJECTIFS DE LA STATISTIQUE DESCRIPTIVE • La statistique descriptive est l’ensemble des méthodes et des techniques permettant de présenter, de décrire, de résumer, des données nombreuses et variées. • Il faut préciser d’abord quel est l’ensemble étudié, appelé population statistique, dont les éléments sont des individus ou unités statistiques. • Chaque individu est décrit par une ou plusieurs variables, ou caractères statistiques.

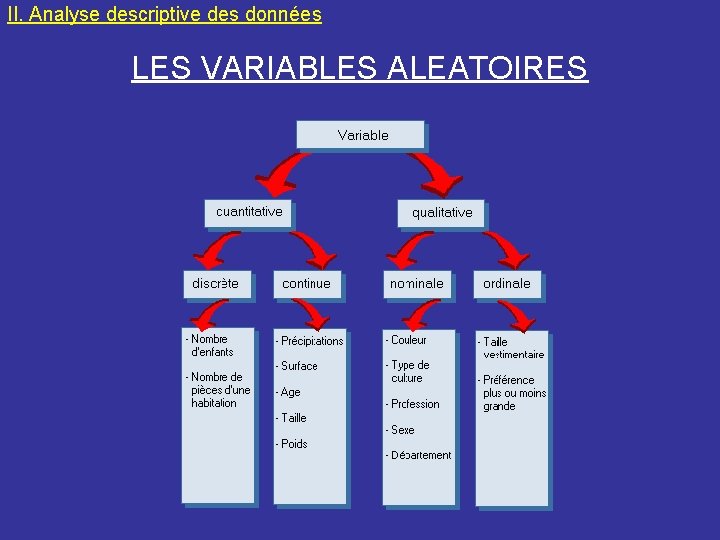
II. Analyse descriptive des données LES VARIABLES ALEATOIRES Chaque variable peut être selon le cas: 1. Quantitative: ses valeurs sont des nombres exprimant une quantité, sur lesquels les opérations arithmétiques (somme, etc…) ont un sens. La variable peut alors être discrète ou continue selon la nature de l'ensemble des valeurs qu'elle est susceptible de prendre (valeurs isolées ou intervalle). 2. Qualitative: ses valeurs sont des modalités, ou catégories, exprimées sous forme littérale ou par un codage numérique sur lequel des opérations arithmétiques n'ont aucun sens.

II. Analyse descriptive des données LES VARIABLES ALEATOIRES

II. Analyse descriptive des données LES VARIABLES ALEATOIRES • On distingue des variables qualitatives ordinales ou nominales, selon que les modalités peuvent être naturellement ordonnées ou pas. • Une variable est dichotomique si elle n'a que 2 modalités. • Les variables seront ensuite analysées différemment selon leur nature (quantitative, qualitative, etc. . . ), au moyen de tableaux, graphiques, calcul de paramètresclé.

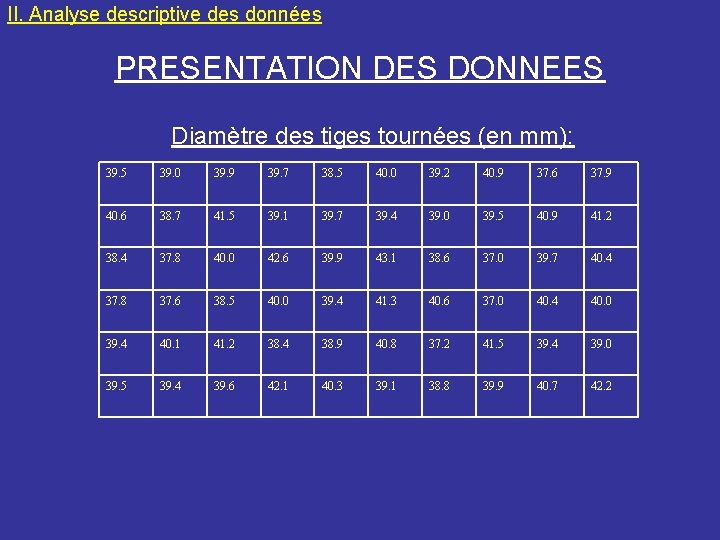
II. Analyse descriptive des données ETUDE D’UN EXEMPLE • Etude du diamètre de tiges tournées: dans un atelier mécanique, on a vérifié le diamètre de tiges tournées sur un tour à commande numérique. La valeur du diamètre n’est pas la même pour toutes les tiges. Le diamètre des tiges devrait normalement se situer entre 36 et 44 mm avec une valeur nominale de 40 mm. Soixante tiges ont été mesurées avec un micromètre de précision et les résultats sont présentés dans un tableau.

II. Analyse descriptive des données PRESENTATION DES DONNEES Diamètre des tiges tournées (en mm): 39. 5 39. 0 39. 9 39. 7 38. 5 40. 0 39. 2 40. 9 37. 6 37. 9 40. 6 38. 7 41. 5 39. 1 39. 7 39. 4 39. 0 39. 5 40. 9 41. 2 38. 4 37. 8 40. 0 42. 6 39. 9 43. 1 38. 6 37. 0 39. 7 40. 4 37. 8 37. 6 38. 5 40. 0 39. 4 41. 3 40. 6 37. 0 40. 4 40. 0 39. 4 40. 1 41. 2 38. 4 38. 9 40. 8 37. 2 41. 5 39. 4 39. 0 39. 5 39. 4 39. 6 42. 1 40. 3 39. 1 38. 8 39. 9 40. 7 42. 2

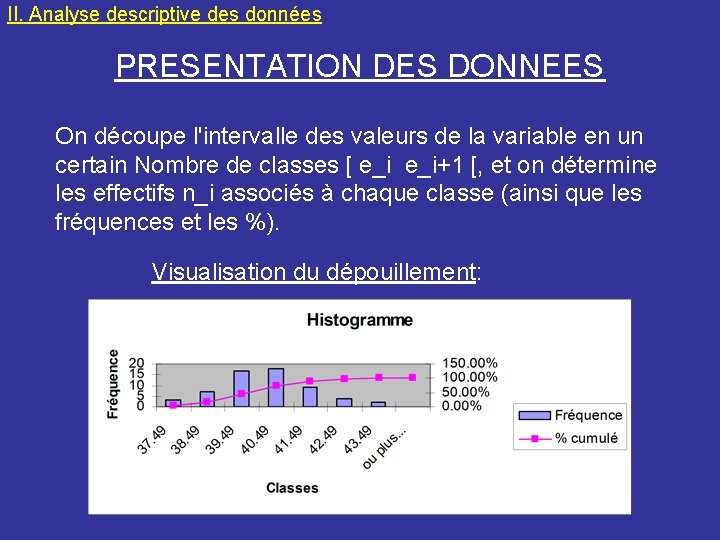
II. Analyse descriptive des données PRESENTATION DES DONNEES • A partir d’un ensemble de données associé à un caractère, communément appelé série numérique, on veut être en mesure d’effectuer une présentation succincte et intelligible: c’est la première phase d’une analyse descriptive des données. On veut donc, à partir d’un ensemble de données, - les ranger par valeurs croissantes - les dépouiller suivant une distribution de fréquence - visualiser ce dépouillement à l’aide d’un histogramme (variable continue) ou d’un diagramme en bâton (variable discrète) A ceci pourra s’ajouter la courbe des fréquences cumulées croissantes.

II. Analyse descriptive des données PRESENTATION DES DONNEES On découpe l'intervalle des valeurs de la variable en un certain Nombre de classes [ e_i+1 [, et on détermine les effectifs n_i associés à chaque classe (ainsi que les fréquences et les %). Visualisation du dépouillement:

III. Paramètres statistiques

III. Paramètres statistiques QU’APPELLE-T-ON PARAMETRES STATISTIQUES Les paramètres statistiques ont pour but de résumer, à partir de quelques nombres clés, l'essentiel de l'information relative à l'observation d'une variable quantitative. On définira plusieurs sortes de paramètres : - Certains, comme la moyenne, seront dits de tendance centrale car ils représentent une valeur numérique autour de laquelle les observations sont réparties. - D'autres, par exemple, seront dits de dispersion car ils permettent de résumer le plus ou moins grand étalement des observations de part et d'autre de la tendance centrale.

III. Paramètres statistiques QU’APPELLE-T-ON PARAMETRES STATISTIQUES • Moyenne, médiane et mode sont des valeurs autour desquelles observations sont réparties; ce sont trois façons complémentaires de caractériser la tendance centrale. • Il peut être important aussi de noter le minimum et le maximum des valeurs observées, la différence entre ces nombres étant l'étendue des mesures.

III. Paramètres statistiques QU’APPELLE-T-ON PARAMETRES STATISTIQUES • Enfin, on peut calculer d'autres paramètres (nous verrons par exemple l'écart-type), qui permettent de quantifier la plus ou moins grande variabilité des mesures, leur dispersion plus ou moins importante de part et d'autre de la tendance centrale, telle qu'on peut la mettre en évidence sous forme graphique:

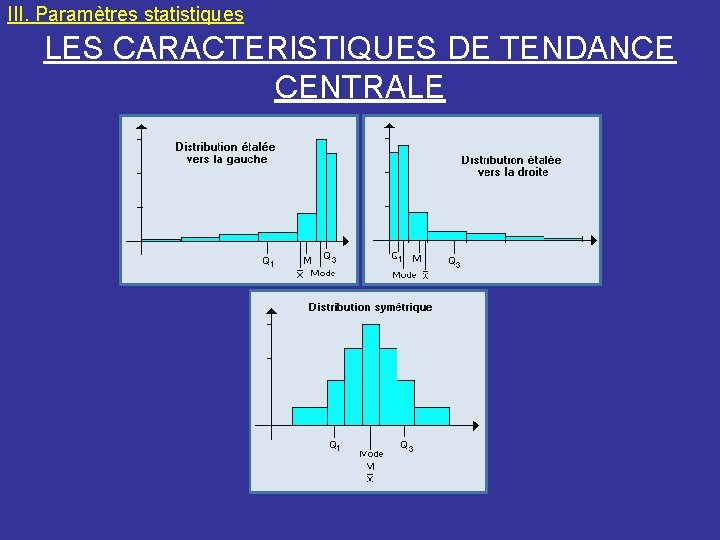
III. Paramètres statistiques LES CARACTERISTIQUES DE TENDANCE CENTRALE • - la moyenne (arithmétique), éventuellement pondérée • - la médiane : M est insensible aux valeurs aberrantes, mais se prête moins bien aux calculs que la moyenne si le nombre de données est important. • - le mode dans le cas particulier d'une distribution unimodale. • la comparaison de ces trois paramètres donne des indications sur la symétrie de la distribution:

III. Paramètres statistiques LES CARACTERISTIQUES DE TENDANCE CENTRALE

III. Paramètres statistiques LES CARACTERISTIQUES DE DISPERSION • étendue • variance et écart-type : calculés généralement en complément de la moyenne, pour mesurer la plus ou moins grande dispersion autour de celle-ci. • intervalle interquartile : sa longueur, l'écart-interquartile mesure la dispersion des 50 % valeurs les plus centrales. • le diagramme en boîte (ou boîte à moustaches) représente les quartiles, et les valeurs extrêmes, en repérant les éventuelles valeurs aberrantes:

III. Paramètres statistiques CALCULS DE LA MOYENNE ET DE LA VARIANCE • Les calculs des paramètres de tendance centrale et de dispersion (moyenne et variance) correspondent à des calculs de centre de gravité et de moment d’inertie en mécanique: on parle alors respectivement de moment d’ordre 1 et de moment d’ordre 2. • C’est par rapport au centre de gravité que le moment d’inertie est minimum (par rapport à la moyenne que la variance est minimum). Une méthode de moindres carrés conduit à choisir la moyenne comme meilleur paramètre de tendance centrale d’un caractère X (voir TD).

III. Paramètres statistiques CONCLUSION SUR LES PARAMETRES STATISTIQUES • Pour résumer une série unidimensionnelle, il faut toujours la représenter par un ou deux graphiques appropriés, et plusieurs paramètres de tendance centrale, de position et de dispersion. • L'étude et la comparaison de ces paramètres permet de bien caractériser la distribution, et de repérer d'éventuelles données aberrantes.

IV. Introduction au calcul des probabilités

III. Introduction au calcul des probabilités EXPERIENCE ALEATOIRE Lançons un dé cubique à 6 faces: Lorsque ce dé se sera immobilisé, on lira le numéro qui apparaît sur la face supérieure. Le numéro qui apparaît sur la face supérieure ne peut pas être prévu. L'expérience qui consiste à lancer un dé est une expérience aléatoire. Il y a six résultats ou issues possibles à cette expérience, l'un des nombres : 1, 2, 3, 4, 5, 6 Mais à chaque répétition ou épreuve de l'expérience, on ne peut pas prévoir quelle en sera l'issue.

III. Introduction au calcul des probabilités EVENEMENT LIE A UNE EXPERIENCE ALEATOIRE L’ensemble fondamental ou ensemble des issues s’appelle l’univers des possibles. Lancer le dé, le résultat est-il un trois ? On dira que cette assertion est un événement lié à l'expérience aléatoire: lancer une fois le dé. On dira que cet événement est réalisé ou non suivant que cette proposition est vraie ou fausse après une épreuve de l'expérience aléatoire. A chaque événement est associée une partie de l’ensemble fondamental constituée des issues pour lesquelles l'événement est réalisé. A l'événement « le résultat est pair » est associée la partie A de l’ensemble fondamental formée des nombres pairs.

III. Introduction au calcul des probabilités EVENEMENT LIE A UNE EXPERIENCE ALEATOIRE Si l’ensemble fondamental est fini, à toute partie A de l’ensemble fondamental, est associé un événement, par exemple l'événement « l'issue de l'expérience est un élément de A » . Si l’ensemble fondamental est fini, l’ensemble des parties de l’ensemble fondamental représente l'ensemble des événements associé à l'expérience aléatoire. On appelle événement élémentaire un événement qui n'est réalisé que par une seule issue de l'expérience. L’événement: « le résultat est 3 » est un événement élémentaire

III. Introduction au calcul des probabilités EVENEMENT LIE A UNE EXPERIENCE ALEATOIRE Un événement est dit impossible s'il n'est réalisé par aucune issue de l'expérience aléatoire. A un événement impossible on associe la partie vide. Un événement est dit certain s'il est réalisé par toutes les issues de l'expérience aléatoire.

III. Introduction au calcul des probabilités COMPOSITION DES EVENEMENTS On peut composer les événements à l'aide des connecteurs logiques : ET, OU, NON. Soit A l’événement: Avoir une face paire (2, 4, 6) Soit B l’événement: Avoir un nombre > 4 (5, 6) La conjonction A ET B de ces deux événements est l’événement: A ET B: « le résultat est un nombre pair ET il est > 4 » A l'événement A ET B est associée l'intersection des parties associées à A ET B:

III. Introduction au calcul des probabilités COMPOSITION DES EVENEMENTS A l'événement A OU B est associée la réunion des parties associées à A OU B. La négation de l’événement A est non A (c’est-à-dire avoir une face impaire). Deux événements A et B sont dits incompatibles s'il n'existe pas d'issues à l'expérience réalisant simultanément A et B. Si A et B sont incompatibles, les parties de l’ensemble fondamental qui leur sont associées ont une intersection vide. L'ensemble des parties de l’ensemble fondamental, muni des opérations d'union, d'intersection et de complémentation s'appelle l'algèbre des événements liée à l'expérience aléatoire.

III. Introduction au calcul des probabilités COMPOSITION DES EVENEMENTS Soit l'ensemble des issues d'une expérience aléatoire E : A 1 , A 2 , . . . , An n événements liés à cette expérience aléatoire constituent un système complet d'événements si : 1. ils sont deux à deux incompatibles 2. leur disjonction est l'événement certain

III. Introduction au calcul des probabilités NOTION DE PROBABILITE Une probabilité peut être définie comme le rapport du nombre de cas favorables au nombre de cas possibles: Pour l’expérience aléatoire du lancer du dé, la probabilité d’avoir 3 est donc de 1 sur 6. Une probabilité est comprise entre 0 et 1. La somme des probabilités de tous les événements incompatibles entre eux est égale à 1. (incompatibles = disjoints) d’où l’axiome des probabilités totales:

III. Introduction au calcul des probabilités AXIOME DES PROBABILITES TOTALES La probabilité de la somme des événements est la somme des probabilités de chacun d’eux lorsque ceux-ci sont incompatibles: P(A) + P(NON A) = 1 On a défini la probabilité à partir de la réalisation d’un événement. On a défini la notion d’événement composé, on va maintenant pouvoir calculer la probabilité d’événements composés, définir la notion d’indépendance et calculer des probabilités conditionnelles:

III. Introduction au calcul des probabilités CALCUL DE PROBABILITES D’EVENEMENTS COMPOSES Reprenons l’exemple du lancer de dé: Quelle est la probabilité d’avoir l’événement A: une face paire (2, 4, 6) OU d’avoir l’événement B: un nombre > 4 (5, 6) ? P(A OU B) = ? Ici les événements ne sont plus incompatibles, on observe que 6 est compté deux fois, il faut prendre soin de retirer l’un des doubles comptages: il y a alors 4 cas favorables: P(A ou B) = 4/6 = P(A) + P(B) – P(A ET B) La probabilité de A ET B, l’intersection de A avec B est représentée par le 6, donc P(A ET B) = 1/6

III. Introduction au calcul des probabilités CALCUL DE PROBABILITES D’EVENEMENTS COMPOSES Si les deux événements sont incompatibles, alors les sousensembles qui les caractérisent sont disjoints: P(A ET B) = 0 Donc P(A OU B) = P(A) + P(B) Par exemple P(Chiffre impair OU Chiffre Pair) = 3/6 +3/6=1. A l’inverse, si des événements interfèrent, les ensembles correspondants sont sécants. On parle alors de probabilité conditionnelle.

III. Introduction au calcul des probabilités CALCUL DE PROBABILITES CONDITIONNELLES Une probabilité conditionnelle est une probabilité qu’un événement se réalise sachant qu’un autre est déjà réalisé. Par exemple, quelle est la probabilité d’avoir un 5 (événement A) sachant que le nombre lu, une fois le dé arrêté, est impair (événement B). On note cette probabilité P(A/B) = 1/3 = P(A ET B): P(B) P(A/B) se lit P(A si B). On a en effet P(A: avoir un nombre impair) = 3/6, P(A: avoir un nombre impair ET B: avoir un 5) = 1/6 donc P(A/B) = 1/6/3/6 = 1/3. Si les deux événements sont indépendants alors: P(A/B)=P(A) et la probabilité pour que deux événements indépendants se réalisent vaut: P(A ET B)=P(A)x. P(B)

III. Introduction au calcul des probabilités EXEMPLE D’APPLICATION DU CALCUL DE PROBABILITES A LA PRODUCTIQUE Une usine produit des pièces mécaniques identiques à l’aide de 3 machines M 1, M 2 et M 3, d’ancienneté différente. Celles-ci assurent respectivement 50%, 30% et 20% de la production avec des proportions de défectueuses égales à 1%, 2% et 5% Questions: 1. Quelle est la probabilité qu’une pièce mécanique en provenance de cette usine, soit défectueuse ? 2. Quelle est la probabilité qu’une pièce mécanique en provenance de cette usine ne soit pas défectueuse ? 3. Etc….

III. Introduction au calcul des probabilités DENOMBREMENT POUR LE CALCUL DE PROBABILITES Le rapport du nombre de cas favorables au nombre de cas possibles permet de connaître la probabilité d’un événement. Ce rapport, pour être établi, nécessite d’utiliser les outils qu’apporte le dénombrement.

III. Introduction au calcul des probabilités LES PERMUTATIONS Définition: une permutation de plusieurs objets est un groupement de ces objets dans un ordre déterminé: Exemple: a c b et b a c sont deux permutations des lettres a, b, c. Deux permutations différent par l’ordre des objets. Pn = n!

III. Introduction au calcul des probabilités LES PERMUTATIONS Pn = n! Démonstration: 1. Etant donnée une permutation de m objets, comment obtenir une permutation de (m+1) objets ? ↑ ↑ ↑ L’objet supplémentaire peut être placé soit entre deux objets: (m-1) positions, soit avant ou après les m objets: deux autres positions possibles. En tout: m-1+2=m+1 positions possibles.

III. Introduction au calcul des probabilités LES PERMUTATIONS Pn = n! Démonstration: 2. Calcul du nombre de permutations de n objets: Pn=? Pour n=1; P 1=1 (a) Pour n=2; P 2=2 (ab) ou (ba) Pour n=3; P 3=3 x 2=6 a b I ↑ ↑ ↑ I Pour n; Pn=?

III. Introduction au calcul des probabilités LES PERMUTATIONS Pour (n-1) objets, il y a Pn-1 permutations. A chacune d’elles correspondent (n-1)+1=n positions différentes du nème objet. Donc: Pn = Pn-1. n Calcul de Pn: Pn = Pn-1. xn Pn-1= Pn-2. (n-1) Pn-2= Pn-3. (n-2) I P 3= P 2. 3 P 1= 1

III. Introduction au calcul des probabilités LES PERMUTATIONS Multiplions membre à membre, puis simplifions: Pn= n. (n-1). (n-2). ------. 3. 2. 1= n!

III. Introduction au calcul des probabilités LES ARRANGEMENTS Définition: un arrangement de x objets, pris dans un ensemble de n objets (x ≤ n), est un groupement de x de ces objets, chacun de ceux-ci occupant une place déterminée. Un arrangement de x objets choisis parmi n vaut n!/(n-x)! Exemple: pour n=5 lettres: a, b, c, d, e Voici des arrangements de x= 3 lettres choisies parmi n= 5: a b e c d e c Les deux premiers sont différents par la nature des objets, les deux derniers sont différents par leur ordre.

III. Introduction au calcul des probabilités LES ARRANGEMENTS Démonstration: Soit un ensemble de n objets que l’on peut ranger dans x cases: n° 1 n° 2 n° 3 n°x - - - - I - - - - -I- - - -I - I - - - - -I - - - I – n I I n. (n-1) I n. (n-1). (n-2) I n. (n-1). (n-2). - - -. [n-(p+1)]

III. Introduction au calcul des probabilités LES ARRANGEMENTS 1. A l’emplacement n° 1, nous pouvons mettre l’un quelconque des n objets. Pour des lettres par exemple, n lettres: a, b, c, d, e, f, etc…, nous pouvons mettre soit a, soit b, soit c, etc …, d’où n manières possibles d’attribuer la place n° 1 2. A l’emplacement n° 2, il y a (n-1) manières possibles et par suite n. (n-1) manières possibles d’attribuer les places n° 1 et n° 2 3. Il y a (n-2) manières possibles d’attribuer la place n° 3 donc n. (n-1). (n-2) manières possibles d’attribuer l’ensemble des places n° 1, n° 2, n° 3 et ainsi de suite jusqu’à l’attribution de la place n°x, pour laquelle il y a n-(x-1) soit (n-x+1) choix possibles.

III. Introduction au calcul des probabilités LES ARRANGEMENTS D’où la formule des arrangements qui donne le nombre d’arrangements de n objets pris x à x: n. (n-1). (n-2). - - -. (n-x+1) L’utilisation de la notation factorielle permet d’écrire cette relation sous la forme: n!/(n-x)!

III. Introduction au calcul des probabilités LES COMBINAISONS Définition: une combinaison de x objets, pris dans un ensemble de n objets (x inférieur ou égal à n), est un groupement de x de ces objets. Une combinaison de x objets choisis parmi n vaut: n!/[x!. (n-x)!] Exemple: pour n= 5 lettres: a, b, c, d, e Voici des combinaisons de x= 3 lettres choisies parmi n= 5: a d e b c e b d e Les combinaisons sont différentes par la nature des objets uniquement, (b d e) et (d e b) par exemple ne sont pas des combinaisons différentes

III. Introduction au calcul des probabilités LES COMBINAISONS Démonstration: soit un ensemble de n objets, considérons l’une quelconque des combinaisons de x objets pris parmi n, par exemple, la combinaison (a d e) de x=3 lettres choisies dans un ensemble de n=5 lettres (a, b, c, d, e). A cette combinaison, correspondent plusieurs permutations, chacune de ces permutations est un arrangement de x objets pris dans un ensemble de n objets. Dans l’exemple, ces arrangements sont: (a d e) (a e d) (d a e) (d e a) (e a d) (e d a) Leur nombre est 6, d’après la relation P 3=3. 2=6 Alors, en multipliant par Px le nombre de combinaisons, on obtient le nombre d’arrangements (voir tableau). Or on a vu que le nombre de permutations Px vaut x! ce qui après calcul donne la relation attendue pour les combinaisons.

V. Lois de probabilité, exemples

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES DISCRETES Les phénomènes étudiés, leurs caractéristiques de position ou de dispersion suivent souvent des densités ou des lois de probabilité. Tant que l’espace de probabilité est discret, le langage que nous venons d’introduire suffit: tout problème peut-être compris en termes de probabilités des résultats individuels, qui sont alors dénombrables (voire fini, comme dans le cas du dé)

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES DISCRETES Exemples: 1. la loi uniforme: permet d’attribuer la même probabilité à chaque unité: 1/n. 2. 2. La loi de poisson: modèle probabiliste qui convient au comptage d’événements rares.

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES DISCRETES 3. Loi de Bernoulli: une expérience aléatoire dont l’issue se traduit soit par un succès, soit par un échec: avoir la probabilité p de tirer une pièce défectueuse et la probabilité (1 -p) de tirer une pièce non défectueuse.

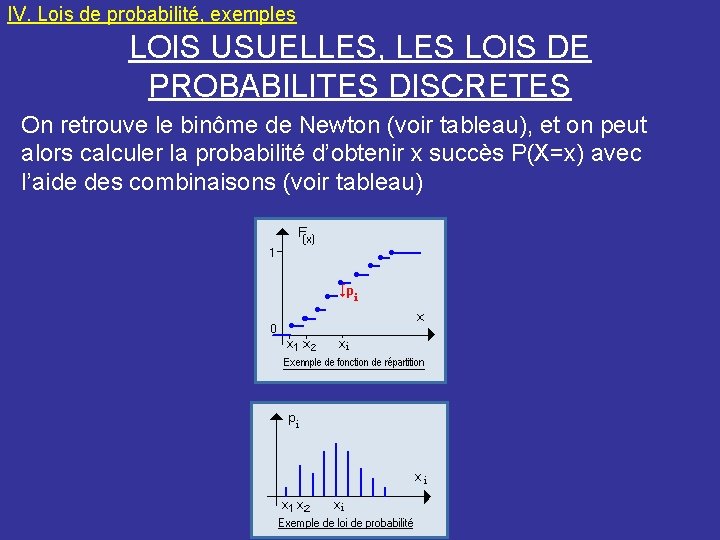
IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES DISCRETES 4. Loi Binômiale: On répète les épreuves de Bernoulli. On s’intéresse donc au nombre de succès ou d’échecs qui se sont produits pour n épreuves de Bernoulli.

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES DISCRETES On retrouve le binôme de Newton (voir tableau), et on peut alors calculer la probabilité d’obtenir x succès P(X=x) avec l’aide des combinaisons (voir tableau)

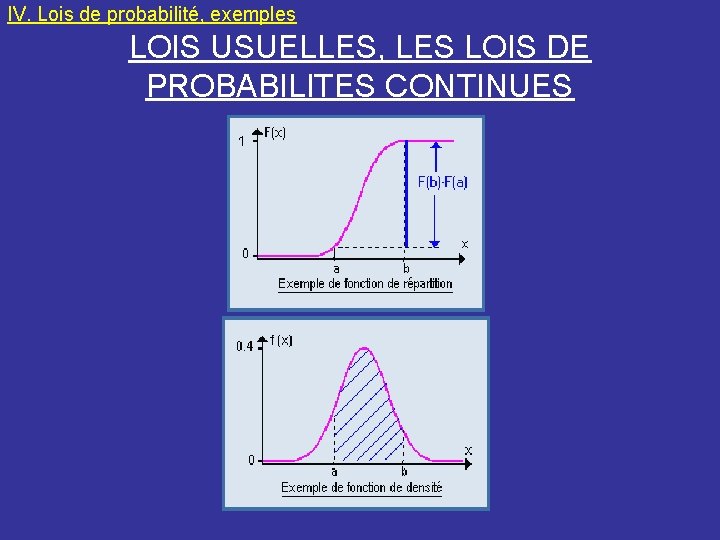
IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES CONTINUES Les problèmes sérieux de probabilité, font appel à des espaces de probabilité qui sont non seulement infinis, mais continus; les événements ne sont pas dénombrables, et le langage de la théorie de la mesure est indispensable. La probabilité d’obtenir exactement une valeur est nulle: un point n’a pas d’épaisseur, donc la surface située exactement sous la fonction densité de probabilité en un point est nulle. On obtient 1 en additionnant un nombre infini de zéros. Cela semble bizarre ? Pourtant une ligne a une longueur, et les points qui la composent sont de longueur nulle. Dans ce cas, les probabilités des résultats individuels ne signifient rien: on est obligé de remplacer les sommes (finies ou infinies) par des intégrales.

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES CONTINUES Exemples 1. La loi uniforme continue: 2. Lorsque la fonction de densité de probabilité est constante sur un intervalle [a, b] et nulle partout ailleurs, on parle de loi uniforme de paramètres a et b.

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES CONTINUES La loi uniforme s’impose naturellement pour les variables dont les valeurs possibles sont bornées, aucune de ces valeurs n’ayant plus de chance d’apparaître que n’importe quelle autre valeur. On la rencontre également dans le cas d’erreur de mesures pour des mesures dites grossières, réalisées avec des instruments dont les divisions ne sont pas très fines, la mesure étant arrondie à l’une de ces divisions.

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES CONTINUES 2. La loi normale ou loi de Gauss-Laplace (courbe en cloche): Tous les phénomènes naturels obéissent à des lois de probabilité plus ou moins compliquées. Lorsqu’une grandeur subit l’influence de nombreuses causes indépendantes, dont aucune d’entre-elles n’est prépondérante, elle obéit à une loi normale. Très souvent et sous certaines conditions (à partir d’un certain rang), il est possible de faire des approximations par des lois normales: (les lois binômiales, de Poisson, du Khi-deux et de Student convergent toutes vers la loi normale à partir d’un certain rang d’où l’extrême importance de l’étude de cette loi. )

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES CONTINUES

IV. Lois de probabilité, exemples LOIS USUELLES, LES LOIS DE PROBABILITES CONTINUES 2. La loi de Student: dans le cas de petits échantillons, la densité de probabilité ne suit pas une loi normale, mais une loi de Student. La distribution de Student ressemble à la distribution normale, toutefois, la première est plus plate et dépend de la taille de l’échantillon. 3. La loi du Khi-deux: c’est une loi d’échantillonnage continue qui trouve son application dans les tests d’adéquation (test de normalité, …). Par exemple, on peut l’utiliser pour comparer des valeurs observées avec des valeurs théoriques attendues.

VI. ECHANTILLONNAGE, ESTIMATION, DECISION

VI. Echantillonnage, estimation, décision ECHANTILLONNAGE ET ESTIMATION: DEFINITION L’échantillonnage est le passage de la population à l’échantillon et l’estimation est le passage inverse de l’échantillon à la population:

VI. Echantillonnage, estimation, décision ECHANTILLONNAGE ET ESTIMATION: DEFINITION La valeur inconnue d’une population, à estimer à partir d’un échantillon est appelée un paramètre. Souvent, le paramètre à estimer est une moyenne, un total, un pourcentage, un écart type ou une variance. Le paramètre de la population estimé à partir d’une statistique sur la base d’un échantillon.

VI. Echantillonnage, estimation, décision EXEMPLE D’ECHANTILLONNAGE: ESTIMATION D’UNE MOYENNE On considère le cas de la distribution d’échantillonnage des moyennes de la population constituée des cinq nombres 2, 3, 6, 8, 11. La moyenne et l’écart type de cette population sont (tableau). Ici, la population est réduite donc on a la possibilité de calculer la moyenne et l’écart type de la population. Mais, dans les cas réels, ces valeurs sont inconnues et on cherche à les estimer à partir de l’échantillon. On cherche tous les échantillons non exhaustifs de taille 2

VI. Echantillonnage, estimation, décision EXEMPLE D’ECHANTILLONNAGE: ESTIMATION D’UNE MOYENNE Soit mé (la moyenne échantillon) l’estimateur obtenu en calculant la moyenne empirique des valeurs obtenues de l’échantillon. mé est une valeur fixe pour un échantillon donné. Mais cette valeur peut varier suivant le choix de l’échantillon. Il y aura autant de moyennes à calculer qu’il y aura d’échantillons: mé est une variable aléatoire. Les moyennes mé de ces échantillons sont: (tableau) On peut écrire tous les échantillons possibles car la population est fini et réduite, on peut trouver toutes les moyennes des échantillons.

VI. Echantillonnage, estimation, décision EXEMPLE D’ECHANTILLONNAGE: ESTIMATION D’UNE MOYENNE Dans le cas d’une population avec un grand nombre d’individus, la moyenne échantillon est distribuée suivant une loi de probabilité appelée distribution d’échantillonnage des moyennes. La moyenne de la distribution d’échantillonnage des moyennes est égale à la moyenne de la population. (le vérifier) L’écart type de la distribution d’échantillonnage des moyennes est égal à l’écart type de la population divisée par la racine carrée de la taille n (ici n=2) des échantillons. (le vérifier sur cet exemple).

VI. Echantillonnage, estimation, décision NOTION D’INTERVALLE DE CONFIANCE METHODE DE CONSTRUCTION Il ne s’agit plus d’estimer un paramètre inconnu, la moyenne de la population, par un nombre , mais de situer cette moyenne dans un intervalle avec un risque d’erreur connu. Soit θ un paramètre à étudier et T son estimateur à partir d’un échantillon aléatoire. A partir de la loi de distribution de l’estimateur T, on détermine un intervalle calculé sur la base de l’échantillon tel que la probabilité soit importante qu’il englobe la vraie valeur du paramètre recherché. Soit (T-e, T+e) cet intervalle, et (1 -α) la probabilité d’appartenance, on peut dire que la marge d’erreur e est liée à α par la probabilité: P(T-e<θ<T+e)=1 -α

VI. Echantillonnage, estimation, décision NOTION D’INTERVALLE DE CONFIANCE METHODE DE CONSTRUCTION Le niveau de probabilité associé à un intervalle d’estimation est appelé niveau de confiance ou degré de confiance. Voir exemple en TD pour la construction et la prise de décision qui en découle: on abordera alors les tests d’hypothèses statistiques.

VII. Cartes de contrôle, capabilité d’un procédé

VII. Cartes de contrôle, capabilité d’un procédé NOTION DE CAPABILITE La capabilité du procédé dépend des cinq M: Méthode, Machine, Main d’œuvre, Matière, Milieu. La capabilité est le ratio de l’intervalle de tolérance par la largeur de la distribution qui vaut environ 6. σ. Cp= capabilité du processus=IT/ 6. σ Avec IT: intervalle de tolérance sigma: l’estimation de l’écart type de la population On peut distinguer 3 cas (voir tableau) Mais il est difficile de centrer le procédé, d’où l’introduction Cpk. (voir tableau).

VII. Cartes de contrôle, capabilité d’un procédé CARTES DE CONTROLE Le pilotage du processus peut alors être réalisé à l’aide de cartes de contrôle. On ajoute le temps, l’objectif est de détecter un déréglage du processus avant l’émission de rebuts.